文章目录
- [一、Bézier 曲线](#一、Bézier 曲线)
前言:
在计算机图形学、动画设计、字体排版乃至汽车制造等领域,有一种数学工具被广泛使用,它既能精确描述复杂的曲线形状,又具备直观的几何控制方式这就是贝塞尔曲线(Bézier Curve)。
一、Bézier 曲线
1、历史背景
贝塞尔曲线得名于法国工程师皮埃尔·贝塞尔(Pierre Bézier),他在20世纪60年代为雷诺汽车公司工作时,将其用于汽车车身的计算机辅助设计(CAD)。然而,几乎同时,另一位法国数学家保罗·德·卡斯特里奥在雪铁龙公司也独立发展出了一种类似的算法(即著名的 de Casteljau 算法)。尽管卡斯特里奥的工作更早完成,但由于其成果属于公司机密,直到多年后才公开,因此这一曲线最终以贝塞尔的名字广为人知。
2、定义
贝塞尔曲线是一种在计算机图形学中广泛使用的参数曲线 ,它由一组控制点定义 ,并通过一个参数
t来生成平滑的曲线路径。

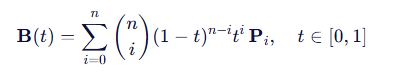
3、常见低阶 Bézier 曲线

4、高阶 Bézier 曲线

5、关键性质
- 端点插值 :曲线始终从
P0开始,在Pn结束。 - 凸包性:曲线完全位于其控制点的凸包内部。
- 对称性:若将控制点顺序反转,得到的曲线相同但方向相反。
- 变差缩减性:曲线不会比控制多边形"振荡"更剧烈。
- 可细分性 :可通过
de Casteljau算法将曲线分割为两段,每段仍是Bézier曲线。
6、de Casteljau 算法
这是计算贝塞尔曲线上某一点的数值稳定且直观的方法。以三次贝塞尔曲线为例:
- 对每对相邻控制点进行线性插值,得到三个新点;
- 对这三个新点再次插值,得到两个点;
- 最后对这两个点插值得到曲线上对应参数 t 的点。
该算法不仅用于求值,还可用于曲线细分,在渲染和碰撞检测中非常有用。