如图所示，点 v v v 绕原点旋转 θ \theta θ 角后得到点 v ′ v' v′。设点 v v v 的坐标为 ( x , y ) (x, y) (x,y)，原点到点 v v v 的距离为 r r r，原点与点 v v v 构成的向量与 x x x 轴的夹角为 ϕ \phi ϕ，则点 v v v 的坐标可表示为：
x = r cos ϕ , y = r sin ϕ x = r\cos\phi, \quad y = r\sin\phi x=rcosϕ,y=rsinϕ
点 v ′ v' v′ 的坐标 ( x ′ , y ′ ) (x', y') (x′,y′) 满足：
x ′ = r cos ( θ + ϕ ) , y ′ = r sin ( θ + ϕ ) x' = r\cos(\theta + \phi), \quad y' = r\sin(\theta + \phi) x′=rcos(θ+ϕ),y′=rsin(θ+ϕ)
根据三角函数和角公式展开：
x ′ = r cos θ cos ϕ − r sin θ sin ϕ y ′ = r sin θ cos ϕ + r cos θ sin ϕ x' = r\cos\theta\cos\phi - r\sin\theta\sin\phi \\ y' = r\sin\theta\cos\phi + r\cos\theta\sin\phi x′=rcosθcosϕ−rsinθsinϕy′=rsinθcosϕ+rcosθsinϕ
将 x = r cos ϕ x = r\cos\phi x=rcosϕ 与 y = r sin ϕ y = r\sin\phi y=rsinϕ 代入上式，化简得：
x ′ = x cos θ − y sin θ y ′ = x sin θ + y cos θ x' = x\cos\theta - y\sin\theta \\ y' = x\sin\theta + y\cos\theta x′=xcosθ−ysinθy′=xsinθ+ycosθ
写成矩阵形式为：
x ′ y ′ \] = \[ cos θ − sin θ sin θ cos θ \] ⋅ \[ x y \] \\begin{bmatrix} x' \\\\ y' \\end{bmatrix} = \\begin{bmatrix} \\cos\\theta \& -\\sin\\theta \\\\ \\sin\\theta \& \\cos\\theta \\end{bmatrix} \\cdot \\begin{bmatrix} x \\\\ y \\end{bmatrix} \[x′y′\]=\[cosθsinθ−sinθcosθ\]⋅\[xy
设平移矩阵为 T ( t x , t y ) T(t_x, t_y) T(tx,ty)（表示沿 x x x 轴平移 t x t_x tx、沿 y y y 轴平移 t y t_y ty），则绕任意点的旋转变换可表示为：
v ′ = T ( t x , t y ) ⋅ R ( θ ) ⋅ T ( − t x , − t y ) ⋅ v v' = T(t_x, t_y) \cdot R(\theta) \cdot T(-t_x, -t_y) \cdot v v′=T(tx,ty)⋅R(θ)⋅T(−tx,−ty)⋅v
其中， v v v 为原始点坐标， v ′ v' v′ 为旋转后点坐标， R ( θ ) R(\theta) R(θ) 为绕原点的旋转矩阵。由于采用列向量表示点坐标，矩阵运算遵循左乘规则，先执行平移 T ( − t x , − t y ) T(-t_x, -t_y) T(−tx,−ty) 将旋转中心移至原点。
在计算机图形学中，为统一描述平移、旋转、缩放等变换，需引入齐次坐标。二维变换中，齐次坐标采用 ( x , y , w ) (x, y, w) (x,y,w) 表示（通常取 w = 1 w=1 w=1），通过 3×3 矩阵实现各类变换的统一表达（三维变换则需 4×4 矩阵）。
3.1 二维平移的矩阵表示
如图所示，点 P ( x , y ) P(x, y) P(x,y) 沿 x x x 轴平移 t x t_x tx、沿 y y y 轴平移 t y t_y ty 后得到点 P ′ ( x ′ , y ′ ) P'(x', y') P′(x′,y′)，其坐标关系为：
x ′ = x + t x , y ′ = y + t y x' = x + t_x, \quad y' = y + t_y x′=x+tx,y′=y+ty
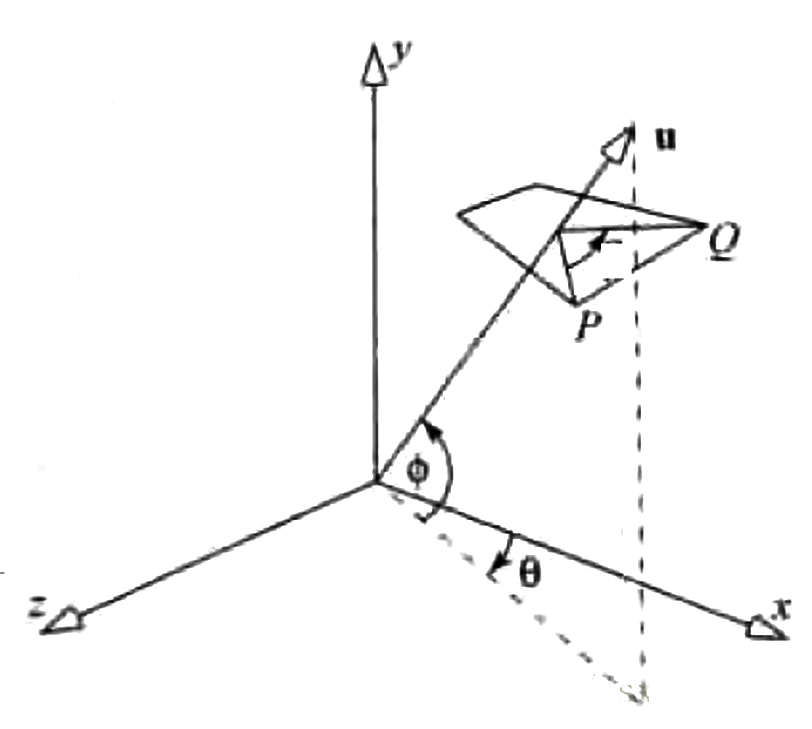
采用齐次坐标表示为： x ′ y ′ 1 = 1 0 t x 0 1 t y 0 0 1 ⋅ x y 1 \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} x′y′1 = 100010txty1 ⋅ xy1
因此，二维平移矩阵为：
T ( t x , t y ) = 1 0 t x 0 1 t y 0 0 1 T(t_x, t_y) = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} T(tx,ty)= 100010txty1
若平移量为 ( − t x , − t y ) (-t_x, -t_y) (−tx,−ty)，则平移矩阵为：
T ( − t x , − t y ) = 1 0 − t x 0 1 − t y 0 0 1 T(-t_x, -t_y) = \begin{bmatrix} 1 & 0 & -t_x \\ 0 & 1 & -t_y \\ 0 & 0 & 1 \end{bmatrix} T(−tx,−ty)= 100010−tx−ty1
3.2 二维旋转矩阵的齐次坐标扩展
将第 2 节中的绕原点旋转矩阵扩展为 3×3 形式，以适配齐次坐标： x ′ y ′ 1 = cos θ − sin θ 0 sin θ cos θ 0 0 0 1 ⋅ x y 1 \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} x′y′1 = cosθsinθ0−sinθcosθ0001 ⋅ xy1
3.3 绕任意点的旋转矩阵推导
结合平移矩阵与旋转矩阵，绕任意点 ( t x , t y ) (t_x, t_y) (tx,ty) 旋转 θ \theta θ 角的复合矩阵为：
M = T ( t x , t y ) ⋅ R ( θ ) ⋅ T ( − t x , − t y ) M = T(t_x, t_y) \cdot R(\theta) \cdot T(-t_x, -t_y) M=T(tx,ty)⋅R(θ)⋅T(−tx,−ty)
代入各矩阵表达式并展开：
M = 1 0 t x 0 1 t y 0 0 1 ⋅ cos θ − sin θ 0 sin θ cos θ 0 0 0 1 ⋅ 1 0 − t x 0 1 − t y 0 0 1 = cos θ − sin θ ( 1 − cos θ ) t x + t y sin θ sin θ cos θ ( 1 − cos θ ) t y − t x sin θ 0 0 1 \begin{align*} M &= \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & -t_x \\ 0 & 1 & -t_y \\ 0 & 0 & 1 \end{bmatrix} \\ &= \begin{bmatrix} \cos\theta & -\sin\theta & (1-\cos\theta)t_x + t_y\sin\theta \\ \sin\theta & \cos\theta & (1-\cos\theta)t_y - t_x\sin\theta \\ 0 & 0 & 1 \end{bmatrix} \end{align*} M= 100010txty1 ⋅ cosθsinθ0−sinθcosθ0001 ⋅ 100010−tx−ty1 = cosθsinθ0−sinθcosθ0(1−cosθ)tx+tysinθ(1−cosθ)ty−txsinθ1
4. 三维基本旋转
三维旋转变换可分解为绕三个坐标轴（ x x x、 y y y、 z z z 轴）的基本旋转组合，因此需先明确绕单一坐标轴的旋转矩阵。本文采用 OpenGL 标准的右手坐标系，旋转角度的正负遵循右手定则（大拇指指向坐标轴正方向，四指弯曲方向为角度正方向），如图所示：
4.1 绕 x x x 轴的旋转
点 P ( x , y , z ) P(x, y, z) P(x,y,z) 绕 x x x 轴旋转 θ \theta θ 角后得到点 P ′ ( x ′ , y ′ , z ′ ) P'(x', y', z') P′(x′,y′,z′)。由于旋转过程中 x x x 坐标保持不变， y y y 与 z z z 坐标的变化等价于在 y o z yoz yoz 平面内的二维旋转（ y y y 轴对应二维旋转的 x x x 轴， z z z 轴对应二维旋转的 y y y 轴），因此：
x ′ = x y ′ = y cos θ − z sin θ z ′ = y sin θ + z cos θ x' = x \\ y' = y\cos\theta - z\sin\theta \\ z' = y\sin\theta + z\cos\theta x′=xy′=ycosθ−zsinθz′=ysinθ+zcosθ
采用齐次坐标（4×4 矩阵）表示为： x ′ y ′ z ′ 1 = 1 0 0 0 0 cos θ − sin θ 0 0 sin θ cos θ 0 0 0 0 1 ⋅ x y z 1 \begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta & 0 \\ 0 & \sin\theta & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} x′y′z′1 = 10000cosθsinθ00−sinθcosθ00001 ⋅ xyz1
4.2 绕 y y y 轴的旋转
点 P ( x , y , z ) P(x, y, z) P(x,y,z) 绕 y y y 轴旋转 θ \theta θ 角后得到点 P ′ ( x ′ , y ′ , z ′ ) P'(x', y', z') P′(x′,y′,z′)。旋转过程中 y y y 坐标保持不变， x x x 与 z z z 坐标的变化等价于在 z o x zox zox 平面内的二维旋转（ z z z 轴对应二维旋转的 x x x 轴， x x x 轴对应二维旋转的 y y y 轴），因此：
x ′ = x cos θ + z sin θ y ′ = y z ′ = − x sin θ + z cos θ x' = x\cos\theta + z\sin\theta \\ y' = y \\ z' = -x\sin\theta + z\cos\theta x′=xcosθ+zsinθy′=yz′=−xsinθ+zcosθ
采用齐次坐标（4×4 矩阵）表示为： x ′ y ′ z ′ 1 = cos θ 0 sin θ 0 0 1 0 0 − sin θ 0 cos θ 0 0 0 0 1 ⋅ x y z 1 \begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} \cos\theta & 0 & \sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\theta & 0 & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} x′y′z′1 = cosθ0−sinθ00100sinθ0cosθ00001 ⋅ xyz1
4.3 绕 z z z 轴的旋转
点 P ( x , y , z ) P(x, y, z) P(x,y,z) 绕 z z z 轴旋转 θ \theta θ 角后得到点 P ′ ( x ′ , y ′ , z ′ ) P'(x', y', z') P′(x′,y′,z′)。旋转过程中 z z z 坐标保持不变， x x x 与 y y y 坐标的变化等价于在 x o y xoy xoy 平面内的二维旋转，因此：
x ′ = x cos θ − y sin θ y ′ = x sin θ + y cos θ z ′ = z x' = x\cos\theta - y\sin\theta \\ y' = x\sin\theta + y\cos\theta \\ z' = z x′=xcosθ−ysinθy′=xsinθ+ycosθz′=z
采用齐次坐标（4×4 矩阵）表示为： x ′ y ′ z ′ 1 = cos θ − sin θ 0 0 sin θ cos θ 0 0 0 0 1 0 0 0 0 1 ⋅ x y z 1 \begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta & 0 & 0 \\ \sin\theta & \cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} x′y′z′1 = cosθsinθ00−sinθcosθ0000100001 ⋅ xyz1
4.4 小结
绕三个坐标轴的旋转矩阵形式具有一致性，其差异源于旋转轴对应的正交平面不同：
绕 x x x 轴旋转：正交平面为 y o z yoz yoz，矩阵非对角元素集中在第 2-3 行与第 2-3 列；
绕 y y y 轴旋转：正交平面为 z o x zox zox，矩阵非对角元素集中在第 1-3 行与第 1-3 列；
绕 z z z 轴旋转：正交平面为 x o y xoy xoy，矩阵非对角元素集中在第 1-2 行与第 1-2 列。
若调整坐标向量的书写顺序（如将 ( x , y , z ) (x, y, z) (x,y,z) 改为 ( z , y , x ) (z, y, x) (z,y,x)），绕 y y y 轴的旋转矩阵可与其他两个轴的旋转矩阵在形式上完全统一，其要点均遵循二维旋转矩阵 cos θ − sin θ sin θ cos θ \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} cosθsinθ−sinθcosθ 的结构。
5. 绕任意轴的三维旋转
绕任意轴的三维旋转可通过坐标变换分解为一系列基本旋转操作，具体思路为：将旋转轴平移并旋转至与某一坐标轴（如 z z z 轴）重合，执行绕该坐标轴的旋转后，再通过逆变换将旋转轴恢复至原始位置。
5.1 问题描述
如图所示，点 P P P 绕向量 u = ( a , b , c ) \boldsymbol{u} = (a, b, c) u=(a,b,c) 旋转 θ \theta θ 角后得到点 Q Q Q，已知点 P P P 的坐标与向量 u \boldsymbol{u} u，求点 Q Q Q 的坐标。
5.2 变换步骤
绕 x x x 轴旋转 α \alpha α 角 ：将向量 u \boldsymbol{u} u 旋转至 x o z xoz xoz 平面；
绕 y y y 轴旋转 − β -\beta −β 角 ：将向量 u \boldsymbol{u} u 旋转至与 z z z 轴重合；
绕 z z z 轴旋转 θ \theta θ 角：执行目标旋转操作；
绕 y y y 轴旋转 β \beta β 角：步骤 2 的逆变换；
绕 x x x 轴旋转 − α -\alpha −α 角：步骤 1 的逆变换。
5.3 各步骤矩阵推导
5.3.1 步骤 1：绕 x x x 轴旋转 α \alpha α 角
设向量 u = ( a , b , c ) \boldsymbol{u} = (a, b, c) u=(a,b,c)，其在 y o z yoz yoz 平面的投影为 ( 0 , b , c ) (0, b, c) (0,b,c)，投影与 z z z 轴的夹角为 α \alpha α。根据三角函数定义：
cos α = c b 2 + c 2 , sin α = b b 2 + c 2 \cos\alpha = \frac{c}{\sqrt{b^2 + c^2}}, \quad \sin\alpha = \frac{b}{\sqrt{b^2 + c^2}} cosα=b2+c2 c,sinα=b2+c2 b
对应的旋转矩阵为：
R x ( α ) = 1 0 0 0 0 c b 2 + c 2 − b b 2 + c 2 0 0 b b 2 + c 2 c b 2 + c 2 0 0 0 0 1 R_x(\alpha) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \frac{c}{\sqrt{b^2 + c^2}} & -\frac{b}{\sqrt{b^2 + c^2}} & 0 \\ 0 & \frac{b}{\sqrt{b^2 + c^2}} & \frac{c}{\sqrt{b^2 + c^2}} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Rx(α)= 10000b2+c2 cb2+c2 b00−b2+c2 bb2+c2 c00001
5.3.2 步骤 2：绕 y y y 轴旋转 − β -\beta −β 角
向量 u \boldsymbol{u} u 经步骤 1 旋转后在 x o z xoz xoz 平面的投影与 z z z 轴的夹角为 β \beta β。根据三角函数定义：
cos β = b 2 + c 2 a 2 + b 2 + c 2 , sin β = a a 2 + b 2 + c 2 \cos\beta = \frac{\sqrt{b^2 + c^2}}{\sqrt{a^2 + b^2 + c^2}}, \quad \sin\beta = \frac{a}{\sqrt{a^2 + b^2 + c^2}} cosβ=a2+b2+c2 b2+c2 ,sinβ=a2+b2+c2 a
代入绕 y y y 轴旋转矩阵并替换 θ \theta θ 为 − β -\beta −β，得到：
R y ( − β ) = b 2 + c 2 a 2 + b 2 + c 2 0 − a a 2 + b 2 + c 2 0 0 1 0 0 a a 2 + b 2 + c 2 0 b 2 + c 2 a 2 + b 2 + c 2 0 0 0 0 1 R_y(-\beta) = \begin{bmatrix} \frac{\sqrt{b^2 + c^2}}{\sqrt{a^2 + b^2 + c^2}} & 0 & -\frac{a}{\sqrt{a^2 + b^2 + c^2}} & 0 \\ 0 & 1 & 0 & 0 \\ \frac{a}{\sqrt{a^2 + b^2 + c^2}} & 0 & \frac{\sqrt{b^2 + c^2}}{\sqrt{a^2 + b^2 + c^2}} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Ry(−β)= a2+b2+c2 b2+c2 0a2+b2+c2 a00100−a2+b2+c2 a0a2+b2+c2 b2+c2 00001
步骤 4（绕 y y y 轴旋转 β \beta β 角）的矩阵为 R y ( β ) R_y(\beta) Ry(β)，步骤 5（绕 x x x 轴旋转 − α -\alpha −α 角）的矩阵为 R x ( − α ) R_x(-\alpha) Rx(−α)，二者分别为步骤 2 与步骤 1 矩阵的逆矩阵，仅需将角度替换为相反数即可：
R y ( β ) = b 2 + c 2 a 2 + b 2 + c 2 0 a a 2 + b 2 + c 2 0 0 1 0 0 − a a 2 + b 2 + c 2 0 b 2 + c 2 a 2 + b 2 + c 2 0 0 0 0 1 R_y(\beta) = \begin{bmatrix} \frac{\sqrt{b^2 + c^2}}{\sqrt{a^2 + b^2 + c^2}} & 0 & \frac{a}{\sqrt{a^2 + b^2 + c^2}} & 0 \\ 0 & 1 & 0 & 0 \\ -\frac{a}{\sqrt{a^2 + b^2 + c^2}} & 0 & \frac{\sqrt{b^2 + c^2}}{\sqrt{a^2 + b^2 + c^2}} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Ry(β)= a2+b2+c2 b2+c2 0−a2+b2+c2 a00100a2+b2+c2 a0a2+b2+c2 b2+c2 00001
R x ( − α ) = 1 0 0 0 0 c b 2 + c 2 b b 2 + c 2 0 0 − b b 2 + c 2 c b 2 + c 2 0 0 0 0 1 R_x(-\alpha) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \frac{c}{\sqrt{b^2 + c^2}} & \frac{b}{\sqrt{b^2 + c^2}} & 0 \\ 0 & -\frac{b}{\sqrt{b^2 + c^2}} & \frac{c}{\sqrt{b^2 + c^2}} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Rx(−α)= 10000b2+c2 c−b2+c2 b00b2+c2 bb2+c2 c00001
5.4 复合旋转矩阵
绕任意轴 u \boldsymbol{u} u 旋转 θ \theta θ 角的复合矩阵为各步骤矩阵的左乘组合（按逆变换顺序排列）：
M R = R x ( − α ) ⋅ R y ( β ) ⋅ R z ( θ ) ⋅ R y ( − β ) ⋅ R x ( α ) M_R = R_x(-\alpha) \cdot R_y(\beta) \cdot R_z(\theta) \cdot R_y(-\beta) \cdot R_x(\alpha) MR=Rx(−α)⋅Ry(β)⋅Rz(θ)⋅Ry(−β)⋅Rx(α)
若向量 u \boldsymbol{u} u 为单位向量（满足 a 2 + b 2 + c 2 = 1 a^2 + b^2 + c^2 = 1 a2+b2+c2=1），复合矩阵可简化为：
u 2 + ( 1 − u 2 ) cos θ u v ( 1 − cos θ ) − w sin θ u w ( 1 − cos θ ) + v sin θ 0 u v ( 1 − cos θ ) + w sin θ v 2 + ( 1 − v 2 ) cos θ v w ( 1 − cos θ ) − u sin θ 0 u w ( 1 − cos θ ) − v sin θ v w ( 1 − cos θ ) + u sin θ w 2 + ( 1 − w 2 ) cos θ 0 0 0 0 1 \begin{bmatrix} u^2 + (1 - u^2)\cos\theta & uv(1 - \cos\theta) - w\sin\theta & uw(1 - \cos\theta) + v\sin\theta & 0 \\ uv(1 - \cos\theta) + w\sin\theta & v^2 + (1 - v^2)\cos\theta & vw(1 - \cos\theta) - u\sin\theta & 0 \\ uw(1 - \cos\theta) - v\sin\theta & vw(1 - \cos\theta) + u\sin\theta & w^2 + (1 - w^2)\cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} u2+(1−u2)cosθuv(1−cosθ)+wsinθuw(1−cosθ)−vsinθ0uv(1−cosθ)−wsinθv2+(1−v2)cosθvw(1−cosθ)+usinθ0uw(1−cosθ)+vsinθvw(1−cosθ)−usinθw2+(1−w2)cosθ00001
三维空间中，围绕 x x x、 y y y、 z z z 轴的旋转可形成多种组合顺序，主要分为两类：
Proper Euler 角（经典欧拉角） ：旋转轴包含两次同一坐标轴的旋转，剩余一次为其他坐标轴，共 6 种组合： z z z- x x x- z z z、 x x x- y y y- x x x、 y y y- z z z- y y y、 z z z- y y y- z z z、 x x x- z z z- x x x、 y y y- x x x- y y y；
Tait-Bryan 角 ：旋转轴为三个不同坐标轴的组合，共 6 种组合： x x x- y y y- z z z、 y y y- z z z- x x x、 z z z- x x x- y y y、 x x x- z z z- y y y、 z z z- y y y- x x x、 y y y- x x x- z z z。这类角度也被称为 Cardan 角、航海角（heading-elevation-bank）或姿态角（yaw-pitch-roll）。
后续调整 yaw 或 roll 时，两者效果完全一致，飞机无法实现绕原偏航轴的旋转，即丢失一个自由度。
3.3 数学本质
以 Tait-Bryan 角 z z z- y y y- x x x 顺序（外旋）为例，其对应的旋转矩阵为：
R = R z ( α ) ⋅ R y ( β ) ⋅ R x ( γ ) R = R_z(\alpha) \cdot R_y(\beta) \cdot R_x(\gamma) R=Rz(α)⋅Ry(β)⋅Rx(γ)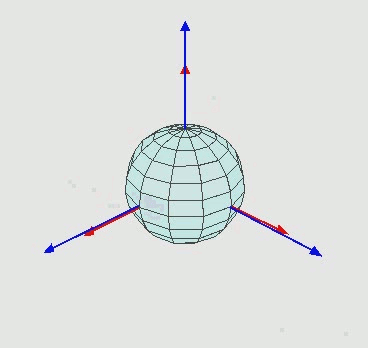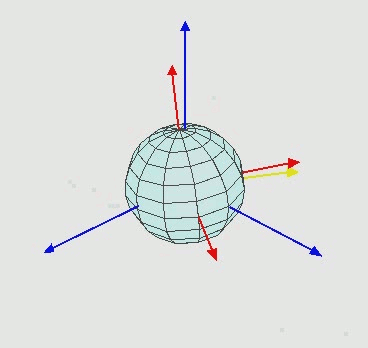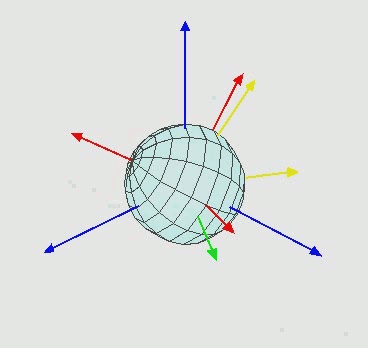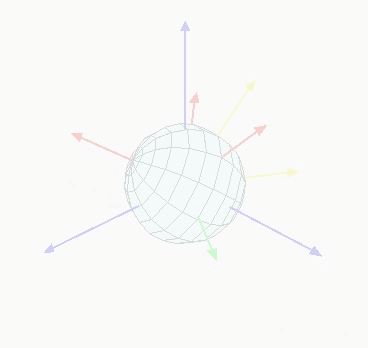
如图所示，分别绕原坐标系的 z z z 轴（蓝色）、一次旋转后的 x x x 轴（绿色）以及两次旋转后的 z z z 轴（红色）旋转，最终生成的红色坐标系即表示目标方向。
1.1 数学计算
新生成的坐标系 ( X , Y , Z ) (X,Y,Z) (X,Y,Z) 可通过原坐标系 ( x , y , z ) (x,y,z) (x,y,z) 乘以旋转矩阵得到。
( X Y Z ) = M ( x y z ) \begin{pmatrix} X \\ Y \\ Z \end{pmatrix} = M \begin{pmatrix} x \\ y \\ z \end{pmatrix} XYZ =M xyz
M = Rot ( z , γ ) ⋅ Rot ( x , β ) ⋅ Rot ( z , α ) = ( cos γ − sin γ 0 sin γ cos γ 0 0 0 1 ) ( 1 0 0 0 cos β − sin β 0 sin β cos β ) ( cos α − sin α 0 sin α cos α 0 0 0 1 ) = ( cos α cos γ − sin α cos β sin γ − sin α cos γ − cos α cos β sin γ sin β sin γ cos α sin γ + sin α cos β cos γ − sin α sin γ + cos α cos β cos γ − sin β cos γ sin α sin β cos α sin β cos β ) \begin{aligned} M &= \text{Rot}(z, \gamma) \cdot \text{Rot}(x, \beta) \cdot \text{Rot}(z, \alpha) \\ &= \begin{pmatrix} \cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \beta & -\sin \beta \\ 0 & \sin \beta & \cos \beta \end{pmatrix} \begin{pmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} \cos \alpha \cos \gamma - \sin \alpha \cos \beta \sin \gamma & -\sin \alpha \cos \gamma - \cos \alpha \cos \beta \sin \gamma & \sin \beta \sin \gamma \\ \cos \alpha \sin \gamma + \sin \alpha \cos \beta \cos \gamma & -\sin \alpha \sin \gamma + \cos \alpha \cos \beta \cos \gamma & -\sin \beta \cos \gamma \\ \sin \alpha \sin \beta & \cos \alpha \sin \beta & \cos \beta \end{pmatrix} \end{aligned} M=Rot(z,γ)⋅Rot(x,β)⋅Rot(z,α)= cosγsinγ0−sinγcosγ0001 1000cosβsinβ0−sinβcosβ cosαsinα0−sinαcosα0001 = cosαcosγ−sinαcosβsinγcosαsinγ+sinαcosβcosγsinαsinβ−sinαcosγ−cosαcosβsinγ−sinαsinγ+cosαcosβcosγcosαsinβsinβsinγ−sinβcosγcosβ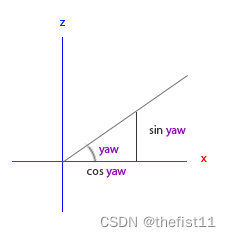
// 计算方向向量的 x 分量
direction.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw));
//译注：direction 表示摄像机的前轴（Front），其方向与本文第一幅图中的第二个摄像机方向向量相反。
// 计算方向向量的 y 分量
direction.y = sin(glm::radians(pitch));
// 计算方向向量的 z 分量
direction.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw));
旋转变换（三）四元数
csxiaoshui 原创于 2017-03-29 11:59:38 发布
1. 简介
四元数（Quaternion）是描述三维旋转的高效数学工具，通过 4 个分量（1 个实部 + 3 个虚部）实现旋转表达，其形式为：
q = s + x i + y j + z k ( s , x , y , z ∈ R ) q = s + xi + yj + zk \quad (s,x,y,z \in \mathbb{R}) q=s+xi+yj+zk(s,x,y,z∈R)
其中虚部满足运算规则：
i 2 = j 2 = k 2 = i j k = − 1 i^2 = j^2 = k^2 = ijk = -1 i2=j2=k2=ijk=−1
四元数的设计灵感源于复数对二维旋转的描述能力，因此先从复数的旋转特性入手理解四元数的本质。
1.1 复数与二维旋转
复数的基本定义为：
z = a + b i ( a , b ∈ R , i 2 = − 1 ) z = a + bi \quad (a,b \in \mathbb{R}, i^2 = -1) z=a+bi(a,b∈R,i2=−1)
1.1.1 复数的运算
共轭复数 ：将虚部取反，记为 z ∗ = a − b i z^* = a - bi z∗=a−bi；
复数的模 ： ∣ z ∣ = a 2 + b 2 |z| = \sqrt{a^2 + b^2} ∣z∣=a2+b2 ；
复数乘法 ： ( a + b i ) ( c + d i ) = ( a c − b d ) + ( a d + b c ) i (a+bi)(c+di) = (ac-bd) + (ad+bc)i (a+bi)(c+di)=(ac−bd)+(ad+bc)i。
1.1.2 复数的旋转意义
复数可映射到复平面（实轴对应 x x x 轴，虚轴对应 y y y 轴），若定义旋转因子：
q = cos θ + i sin θ q = \cos\theta + i\sin\theta q=cosθ+isinθ
则任意复数 z = a + b i z = a+bi z=a+bi 与 q q q 相乘的结果为：
z ′ = q ⋅ z = ( a cos θ − b sin θ ) + ( a sin θ + b cos θ ) i z' = q \cdot z = (a\cos\theta - b\sin\theta) + (a\sin\theta + b\cos\theta)i z′=q⋅z=(acosθ−bsinθ)+(asinθ+bcosθ)i
写成矩阵形式为：
a ′ b ′ \] = \[ cos θ − sin θ sin θ cos θ \] ⋅ \[ a b \] \\begin{bmatrix} a' \\\\ b' \\end{bmatrix} = \\begin{bmatrix} \\cos\\theta \& -\\sin\\theta \\\\ \\sin\\theta \& \\cos\\theta \\end{bmatrix} \\cdot \\begin{bmatrix} a \\\\ b \\end{bmatrix} \[a′b′\]=\[cosθsinθ−sinθcosθ\]⋅\[ab
这与二维旋转矩阵完全一致，说明复数乘法可等价描述复平面内绕原点的旋转。
2. 四元数的定义与运算
复数可描述二维旋转，但直接拓展为"三维复数"（ z = a + b i + c j z = a+bi+cj z=a+bi+cj）会导致乘法不闭合（运算结果超出三维空间）。威廉·哈密顿（William Hamilton）于 1843 年提出四元数，通过引入第四个分量解决了这一问题，并将公式刻于爱尔兰布鲁姆桥（Broom Bridge）。
2.1 四元数的表示形式
四元数有两种常用表示法：
拆分形式： q = s , v q = s, \\boldsymbol{v} q=s,v（ s ∈ R s \in \mathbb{R} s∈R 为实部， v = ( x , y , z ) ∈ R 3 \boldsymbol{v} = (x,y,z) \in \mathbb{R}^3 v=(x,y,z)∈R3 为虚部向量）；
完整形式： q = s + x i + y j + z k q = s + xi + yj + zk q=s+xi+yj+zk（ i , j , k i,j,k i,j,k 为虚部单位，满足 i 2 = j 2 = k 2 = − 1 i^2=j^2=k^2=-1 i2=j2=k2=−1，且 i j = k , j i = − k , j k = i , k j = − i , k i = j , i k = − j ij=k, ji=-k, jk=i, kj=-i, ki=j, ik=-j ij=k,ji=−k,jk=i,kj=−i,ki=j,ik=−j）。
2.2 四元数的基本运算
以下实现基于四元数类 Quat，其成员 _v[4] 存储 ( x , y , z , w ) (x,y,z,w) (x,y,z,w)（ w w w 对应实部 s s s）。
2.2.1 加减法
加法 ：对应分量相加， q 1 + q 2 = ( s 1 + s 2 , x 1 + x 2 , y 1 + y 2 , z 1 + z 2 ) q_1 + q_2 = (s_1+s_2, x_1+x_2, y_1+y_2, z_1+z_2) q1+q2=(s1+s2,x1+x2,y1+y2,z1+z2)；
四元数乘法遵循多项式展开规则，结合虚部运算规则，最终展开式为：
( s 1 + x 1 i + y 1 j + z 1 k ) ( s 2 + x 2 i + y 2 j + z 2 k ) = ( s 1 s 2 − x 1 x 2 − y 1 y 2 − z 1 z 2 ) + ( s 1 x 2 + x 1 s 2 + y 1 z 2 − z 1 y 2 ) i + ( s 1 y 2 − x 1 z 2 + y 1 s 2 + z 1 x 2 ) j + ( s 1 z 2 + x 1 y 2 − y 1 x 2 + z 1 s 2 ) k \begin{align*} &(s_1+x_1i+y_1j+z_1k)(s_2+x_2i+y_2j+z_2k) \\ =& (s_1s_2 - x_1x_2 - y_1y_2 - z_1z_2) \\ &+ (s_1x_2 + x_1s_2 + y_1z_2 - z_1y_2)i \\ &+ (s_1y_2 - x_1z_2 + y_1s_2 + z_1x_2)j \\ &+ (s_1z_2 + x_1y_2 - y_1x_2 + z_1s_2)k \end{align*} =(s1+x1i+y1j+z1k)(s2+x2i+y2j+z2k)(s1s2−x1x2−y1y2−z1z2)+(s1x2+x1s2+y1z2−z1y2)i+(s1y2−x1z2+y1s2+z1x2)j+(s1z2+x1y2−y1x2+z1s2)k
四元数是三维旋转的最优描述方式之一，无万向节死锁问题，且插值平滑、计算高效。其思想是：任意三维旋转可表示为绕单位向量 u \boldsymbol{u} u 旋转 θ \theta θ 角，对应的四元数由旋转轴和旋转角构造。
3.1 绕任意轴旋转的四元数构造
设旋转轴为单位向量 u = ( u x , u y , u z ) \boldsymbol{u} = (u_x, u_y, u_z) u=(ux,uy,uz)，旋转角为 θ \theta θ，则对应的四元数为：
q = cos θ 2 + ( u x i + u y j + u z k ) sin θ 2 q = \cos\frac{\theta}{2} + (u_xi + u_yj + u_zk)\sin\frac{\theta}{2} q=cos2θ+(uxi+uyj+uzk)sin2θ
已知四元数 q = w + x i + y j + z k q = w + xi + yj + zk q=w+xi+yj+zk，反推旋转参数的公式：
θ = 2 arccos ( w ) u = ( x , y , z ) 1 − w 2 ( w ≠ ± 1 ) \begin{align*} \theta &= 2\arccos(w) \\ \boldsymbol{u} &= \frac{(x,y,z)}{\sqrt{1-w^2}} \quad (w \neq \pm1) \end{align*} θu=2arccos(w)=1−w2 (x,y,z)(w=±1)
特殊处理：
w = 1 w=1 w=1（旋转角 0 ∘ 0^\circ 0∘）：分母为 0，直接取 ( x , y , z ) (x,y,z) (x,y,z) 为旋转轴；
w = − 1 w=-1 w=−1（旋转角 18 0 ∘ 180^\circ 180∘）： u = ( x , y , z ) \boldsymbol{u} = (x,y,z) u=(x,y,z)。
实现代码：
cpp复制代码
void getRotate(value_type& angle, value_type& x, value_type& y, value_type& z) const
{
Quat q1 = *this;
if (_v[3] > 1) q1.normalize(); // 确保单位四元数
angle = 2 * acos(q1._v[3]);
value_type s = sqrt(1 - q1._v[3]*q1._v[3]);
if (s < 1e-6) // 旋转角0°
{
x = q1._v[0]; y = q1._v[1]; z = q1._v[2];
}
else // 一般情况
{
x = q1._v[0] / s; y = q1._v[1] / s; z = q1._v[2] / s;
}
}
3.4 四元数旋转向量
将向量 v \boldsymbol{v} v 转换为纯虚四元数 p = 0 + v x i + v y j + v z k p = 0 + v_xi + v_yj + v_zk p=0+vxi+vyj+vzk，旋转后的向量为：
v ′ = q ⋅ p ⋅ q ∗ \boldsymbol{v}' = q \cdot p \cdot q^* v′=q⋅p⋅q∗
四元数的球面插值（Spherical Linear Interpolation）可实现平滑的旋转过渡，公式为：
q t = sin ( ( 1 − t ) θ ) sin θ q a + sin ( t θ ) sin θ q b q_t = \frac{\sin((1-t)\theta)}{\sin\theta}q_a + \frac{\sin(t\theta)}{\sin\theta}q_b qt=sinθsin((1−t)θ)qa+sinθsin(tθ)qb
其中 θ \theta θ 为 q a q_a qa 与 q b q_b qb 的夹角（ cos θ = q a ⋅ q b \cos\theta = q_a \cdot q_b cosθ=qa⋅qb）， t ∈ 0 , 1 t \in 0,1 t∈0,1 为插值因子。
