距离向量场线条绘制算法

距离向量场实现线条绘制的数学推导：

填充范围推导：

先从最简单的假设开始，我希望在AB两点之间画一条粗细为r的线条，并且希望在fragmentShader中直接实现。那么可以这么看待这个问题：

我希望在采样过程中，只要采样点P与AB构成的线段内的任意一点距离<=r,就对fragColor输出颜色，否则就输出0颜色即可。

那么数学化一点的描述就是：求采样点P到到线段AB的最短距离，距离小于r时着色。

如何求采样点P到线段AB的最短距离：

首先我希望有一个点Q

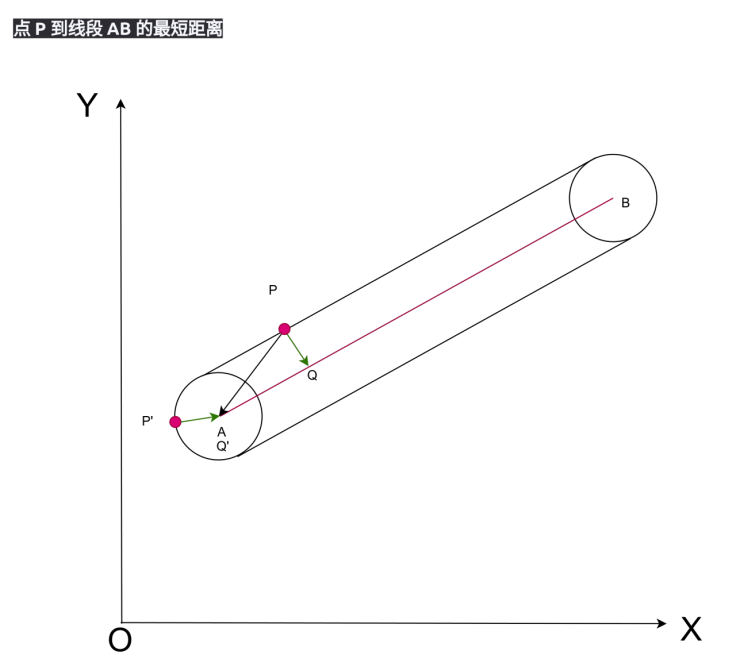
先构成线段BA的向量：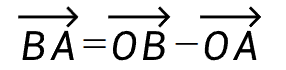

再构成一个采样点P到线段其中一个端点A的向量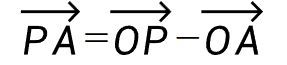：（也可以理解为求出了以点P为原点构成的坐标轴，移动原点的x和y分别为即可到达点A位置）。

而在图上构成了这些向量之后，而现在就可以发现向量AP在向量AB的投影产生的点Q，点Q只能在AB之间移动，所以现在只要让P和Q之间距离小于r的fragment都被着色即可构成颜色被填充的符合目标的封闭区域。而Q可以看作是A点开始，加上比例系数h，乘以线段本身长度AB，h越大就越近B的一个滑点：Q=A+h⋅AB

比例h的大小，取决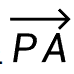于现在投影于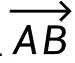的哪个位置。

投影长度：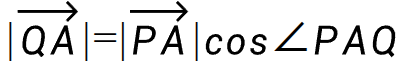

因为使用点积在glsl中可以比较方便地使用dot函数进行计算，所以我故意把它写成：

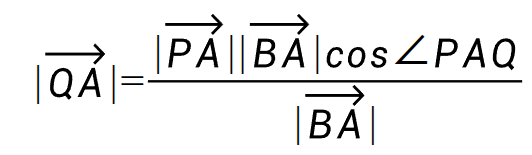
可以看到符合点积形式的算式在分子上。

然后因为我要计算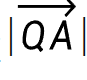占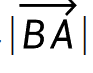的比例h，所以要把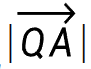除以：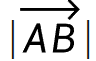

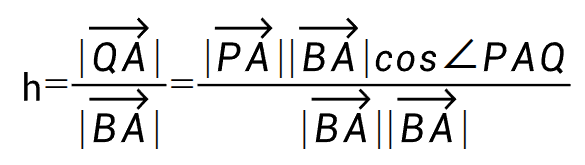
以点积方式描述就是：

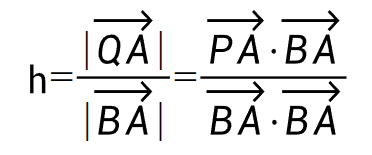
但是我不希望出现h大于1,或者小于0的情况，所以要限制一下值的范围：

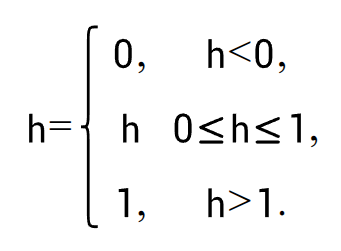
现在可以通过点P的位置知道点Q=A+h⋅AB的位置。

最后每次采样时，采用上述方法迭代计算采样点P和Q之间的距离，只要距离小于r，就在片元出输出颜色即可。

代码实现：

cpp 复制代码

    version 300 es
    precision highp float;

    uniform vec2 u_resolution;
    uniform int u_pointCount;
    uniform vec2 u_points[32];
    uniform float u_strokeWidth;

    out vec4 fragColor;

    // 计算点 p 到线段 ab 的最近距离
    float distanceToSegment(vec2 p, vec2 a, vec2 b) {
        vec2 pa = p - a;
        vec2 ba = b - a;
        float h = clamp(dot(pa, ba) / dot(ba, ba), 0.0, 1.0);
        return length(pa - ba * h);
    }

    void main() {
        vec2 p = gl_FragCoord.xy / u_resolution.xy;
        float halfStrokeWidth = u_strokeWidth * 0.5;
        float minDist = halfStrokeWidth;
        float dist = halfStrokeWidth;  //maxNumber

        // 遍历所有连续线段，获得线段中和采样点最近的线段的最短距离。
        for (int i = 1; i < 32; i++) {
            vec2 a = u_points[i - 1];
            vec2 b = u_points[i];            
dist = min(dist, distanceToSegment(p, a, b));
        }

        // 当P点距离小于r的一半时才设为可见
        float alpha = 0.0;
        if (dist < minDist) {
           alpha = 1.0;
        }
        vec3 color = vec3(0.5, 0.5, 0.5);
        fragColor = vec4(color * alpha, 1.0);
    }

产生效果：

//todo，未完待续