剑指offer-47、求1+2+3...+n

题⽬描述

求 1+2+3+...+n ，要求不能使⽤乘除法、 for 、 while 、 if 、 else 、 switch 、 case 等关键字及条件判断语句（ A?B:C ）。

示例输⼊：5 输出：15

思路及解答

用for循环

这个问题，如果直接使⽤ for 循环，超级简单，重拳出击，时间复杂度为 O(n) 。代码如下：

java 复制代码

public class Solution {
    public int Sum_Solution(int n) {
        int sum = 0;
        for (int i = 1; i <= n; i++) {
            sum += i;
        }
        return sum;
    }
}

可是上⾯的明显违反了使⽤for 循环的原则

乘除法

试试公式法， 1+2+3+...+(n-1)+n = n * (n+1)/2 ,

java 复制代码

public class Solution {
    public int Sum_Solution(int n) {
        if (n >= 0) {
            return n * (n + 1) / 2;
        }
        return 0;
    }
}

但是上⾯的做法，同样是使⽤乘法，也违反了原则，那么要不使⽤循环，也不适⽤乘法，怎么做呢？

递归

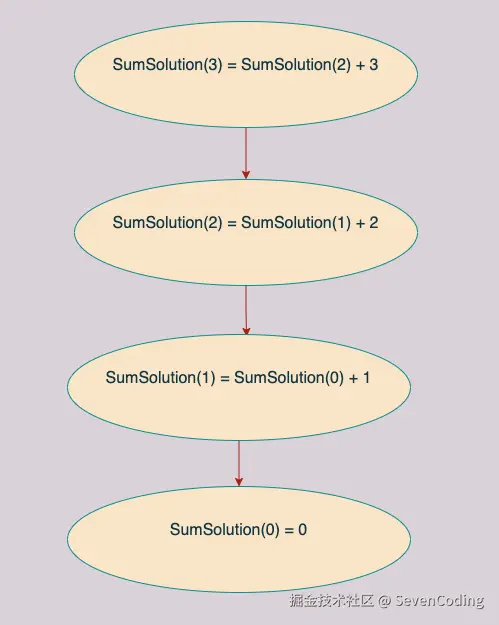
递归可以模拟出循环，⼏乎所有的for 循环操作，都可以以递归的⽅式实现。每⼀次递归，我们让n 减少1 ，直到减少为0 。

java 复制代码

public class Solution {
    public int Sum_Solution(int n) {
        if (n >= 0) {
            return n + Sum_Solution(n - 1);
        }
        return 0;
    }
}

时间复杂度为O(n)
空间复杂度也是O(n)

位运算乘法

位运算乘法法：通过位运算实现乘法操作

思路：将n(n+1)用位运算实现，然后右移1位代替除以2

java 复制代码

public class Solution {
    public int sum(int n) {
        // 计算n*(n+1) using bit manipulation
        int result = multiply(n, n + 1);
        // 右移1位相当于除以2
        return result >> 1;
    }
    
    /**
     * 位运算实现乘法：利用俄罗斯农民算法
     * 原理：a * b = (a << i)的和，其中i对应b中为1的位
     */
    private int multiply(int a, int b) {
        int result = 0;
        
        // 当a不为0时继续循环
        while (a != 0) {
            // 如果a的最低位是1，则加上对应的b值
            if ((a & 1) != 0) {
                result += b;
            }
            // a右移1位，b左移1位
            a >>= 1;
            b <<= 1;
        }
        
        return result;
    }
    
    // 无循环的位运算乘法版本（符合要求）
    public int sumNoLoop(int n) {
        int res = multi(n, n + 1);
        return res >> 1;
    }
    
    private int multi(int a, int b) {
        int res = 0;
        // 通过多个位判断代替循环
        res += ((a & 1) == 1) ? b : 0;
        a >>= 1;
        b <<= 1;
        
        res += ((a & 1) == 1) ? b : 0;
        a >>= 1; 
        b <<= 1;
        
        // 继续处理更多位...（根据n的范围确定需要处理的位数）
        return res;
    }
}

时间复杂度：O(log n) - 取决于数字的位数
空间复杂度：O(1)

案例解析：

text 复制代码

计算 13 × 9:
13 = 1101(二进制)
9 = 1001(二进制)

13 × 9 = 13 × (1 + 0 + 0 + 1) 按位展开
       = (13<<0) + (13<<3) 对应9中为1的位
       = 13 + 104 = 117