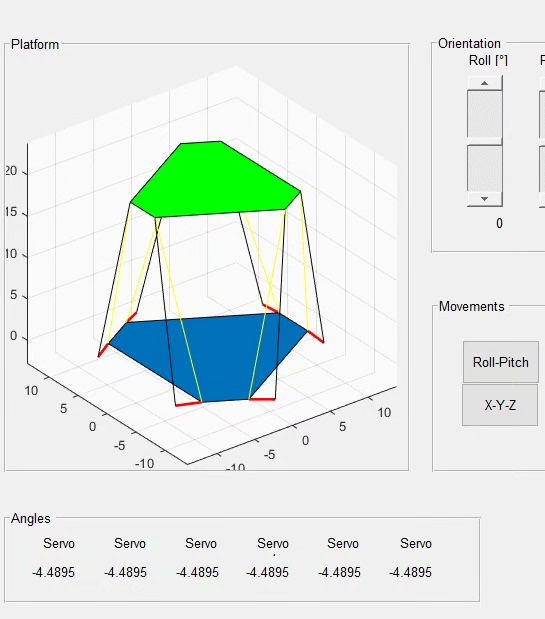
Stewart六自由度平台反解算法详解：基于C#编程语言的实现与应用

Stewart六自由度平台反解算法，c#

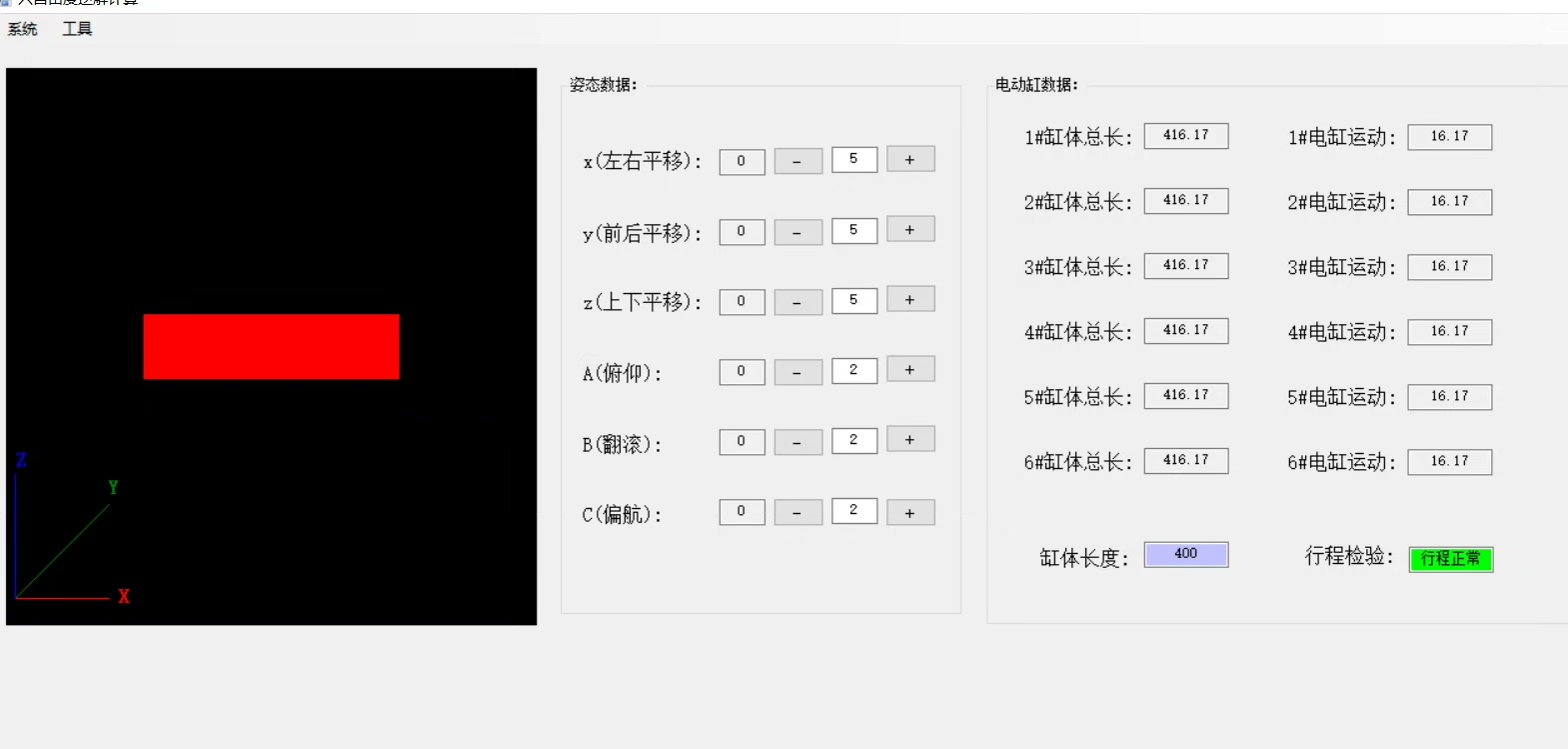
直接上干货，今天咱们聊聊怎么用C#实现Stewart平台的逆解算法。这玩意儿说白了就是已知平台的位置和姿态，反推六个腿该伸多长。先别急着掏线性代数教材，咱们先画个流程图：

确定上下平台坐标系
计算各球铰点的空间坐标
算腿向量长度
搞定！

先整个结构体存平台参数：

csharp 复制代码

public struct StewartPlatform
{
    public float BaseRadius;    // 下平台半径
    public float TopRadius;     // 上平台半径
    public float[][] BaseAngles;// 下平台安装角度（6个）
    public float[][] TopAngles; // 上平台安装角度（6个）
    public float ServoOffset;  // 舵机零位偏移
}

姿态转换是重点，这里用欧拉角转旋转矩阵：

csharp 复制代码

float[] EulerToRotationMatrix(float roll, float pitch, float yaw)
{
    float cr = MathF.Cos(roll), sr = MathF.Sin(roll);
    float cp = MathF.Cos(pitch), sp = MathF.Sin(pitch);
    float cy = MathF.Cos(yaw), sy = MathF.Sin(yaw);

    return new float[9] {
        cy*cp,  cy*sp*sr - sy*cr,  cy*sp*cr + sy*sr,
        sy*cp,  sy*sp*sr + cy*cr,  sy*sp*cr - cy*sr,
        -sp,    cp*sr,           cp*cr
    };
}
// 注意顺序：Z-Y-X旋转，别搞反了！

核心的逆解算法来了：

csharp 复制代码

float[] CalculateLegLengths(StewartPlatform platform, float[] position, float[] euler)
{
    float[] R = EulerToRotationMatrix(euler[0], euler[1], euler[2]);
    float[] lengths = new float[6];

    for (int i = 0; i < 6; i++)
    {
        // 计算上下平台铰点坐标
        float baseAngle = platform.BaseAngles[i];
        Vector3 basePoint = new Vector3(
            platform.BaseRadius * MathF.Cos(baseAngle),
            platform.BaseRadius * MathF.Sin(baseAngle),
            0);

        float topAngle = platform.TopAngles[i];
        Vector3 topPointLocal = new Vector3(
            platform.TopRadius * MathF.Cos(topAngle),
            platform.TopRadius * MathF.Sin(topAngle),
            0);

        // 坐标转换：旋转+平移
        Vector3 topPointGlobal = new Vector3(
            R[0] * topPointLocal.X + R[1] * topPointLocal.Y + R[2] * topPointLocal.Z + position[0],
            R[3] * topPointLocal.X + R[4] * topPointLocal.Y + R[5] * topPointLocal.Z + position[1],
            R[6] * topPointLocal.X + R[7] * topPointLocal.Y + R[8] * topPointLocal.Z + position[2]);

        // 计算腿向量长度
        Vector3 legVector = topPointGlobal - basePoint;
        lengths[i] = legVector.Length() - platform.ServoOffset;
    }
    return lengths;
}
// 注意这里用右手坐标系，Z轴向上

几个容易踩坑的地方：

角度单位：确保所有三角函数参数都是弧度
安装方向：上下平台的点排列顺序要对应
零位校准：ServoOffset要根据实际机械结构测量
数值稳定性：当平台接近奇异位形时要加保护

实测时可以用这个测试用例验证：

csharp 复制代码

// 初始位姿（平台水平，高度1米）
float[] testPos = new float[3] { 0, 0, 1000 };
float[] testEuler = new float[3] { 0, 0, 0 };
var lengths = CalculateLegLengths(myPlatform, testPos, testEuler);
// 六个腿长度应该相等（误差<1mm）

最后别忘了单位转换------机械设计常用毫米，算法中用米会更方便。代码里可以加个转换系数：

csharp 复制代码

const float MetersToMillimeters = 1000f;
// 输入位置用毫米的话记得除以这个系数

实际项目里可能还要处理：

行程限制检查
运动学奇异性检测
关节角度限位
速度/加速度约束

这个算法实测在Unity里驱动虚拟平台能达到60fps，移植到真实控制器时要注意浮点运算精度。下次可以聊聊正解算法------那个才是真·头疼的部分。