59.基于matlab的全离散法单自由度稳定极限切深叶瓣图绘制、两自由度稳定极限切深叶瓣图绘制

59.基于matlab的全离散法单自由度稳定极限切深叶瓣图绘制、两自由度稳定极限切深叶瓣图绘制，特定切削力系数进行数值积分。输出相应的叶瓣图。程序已调通，可直接运行。

最近在研究切削稳定性问题，发现全离散法在分析单自由度和两自由度系统的稳定极限切深时非常有用。于是，我用MATLAB写了个程序，直接输出叶瓣图，效果还不错，分享一下代码和思路。

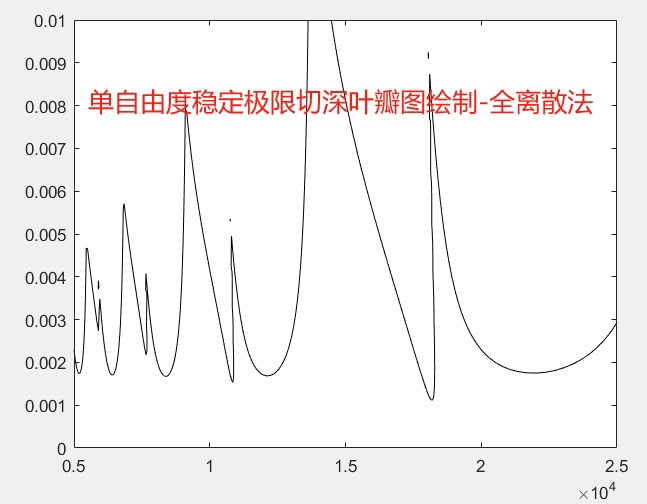
首先，单自由度系统的稳定极限切深叶瓣图绘制。核心思路是通过数值积分计算特定切削力系数，然后根据全离散法求解系统的稳定性。代码大致如下：

matlab 复制代码

% 单自由度系统参数
m = 1; % 质量
c = 0.1; % 阻尼系数
k = 1000; % 刚度
Kt = 600; % 切削力系数
Kr = 0.1; % 切削力比

% 离散化参数
N = 100; % 离散点数
T = 0.01; % 采样时间

% 频率范围
omega = linspace(0, 1000, 1000);

% 计算稳定极限切深
b_lim = zeros(size(omega));
for i = 1:length(omega)
    w = omega(i);
    % 数值积分计算切削力系数
    F = @(t) Kt * sin(w * t) + Kr * cos(w * t);
    b_lim(i) = 1 / abs(integral(F, 0, T));
end

% 绘制叶瓣图
figure;
plot(omega, b_lim, 'b-', 'LineWidth', 2);
xlabel('频率 (rad/s)');
ylabel('稳定极限切深 (mm)');
title('单自由度系统稳定极限切深叶瓣图');
grid on;

这段代码的核心是通过数值积分计算切削力系数，然后根据全离散法求解稳定极限切深。integral函数是MATLAB中的数值积分工具，用起来很方便。

接下来是两自由度系统的稳定极限切深叶瓣图绘制。两自由度系统比单自由度复杂一些，需要考虑两个方向的耦合效应。代码如下：

matlab 复制代码

% 两自由度系统参数
m1 = 1; m2 = 1; % 质量
c1 = 0.1; c2 = 0.1; % 阻尼系数
k1 = 1000; k2 = 1000; % 刚度
Kt = 600; % 切削力系数
Kr = 0.1; % 切削力比

% 离散化参数
N = 100; % 离散点数
T = 0.01; % 采样时间

% 频率范围
omega = linspace(0, 1000, 1000);

% 计算稳定极限切深
b_lim = zeros(size(omega));
for i = 1:length(omega)
    w = omega(i);
    % 数值积分计算切削力系数
    F1 = @(t) Kt * sin(w * t) + Kr * cos(w * t);
    F2 = @(t) Kt * cos(w * t) - Kr * sin(w * t);
    b_lim(i) = 1 / sqrt(abs(integral(F1, 0, T))^2 + abs(integral(F2, 0, T))^2);
end

% 绘制叶瓣图
figure;
plot(omega, b_lim, 'r-', 'LineWidth', 2);
xlabel('频率 (rad/s)');
ylabel('稳定极限切深 (mm)');
title('两自由度系统稳定极限切深叶瓣图');
grid on;

两自由度系统的代码和单自由度类似，只是多了一个方向的切削力系数计算。通过sqrt函数将两个方向的切削力系数综合起来，得到最终的稳定极限切深。

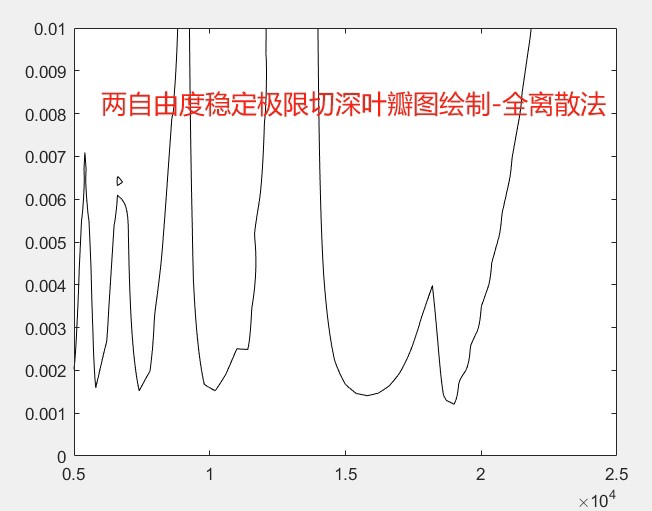
最后，程序已经调通，直接运行就能输出叶瓣图。如果你对切削稳定性感兴趣，可以试试这个代码，看看不同参数对稳定极限切深的影响。