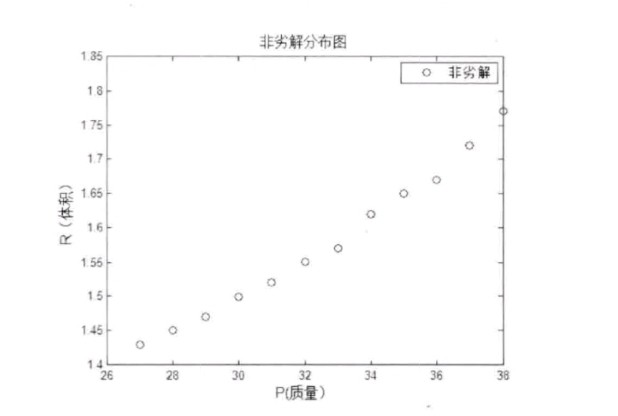
多目标优化求解Pareto题速解

多目标优化求解pareto $1$ 多目标优化问题，可以通过权重法转变成单目标，也可以求解pareto的方法进行解答，获得非劣解集以及pareto前沿 $2$ 可以采取多种优化算法，比如NSGAII，ga,PSO等多种算法 $3$ 通过这个，让你彻底理解和应用多目标优化求解pareto

外卖骑手接单后要在最短时间和最少逆行路段之间做选择，手机厂商研发新品要在性能和散热之间找平衡------现实世界到处是这种互相矛盾的优化目标。传统单目标优化就像拿着锤子找钉子，但面对多目标问题时我们更需要一套组合拳。今天咱们不聊数学公式，直接上手代码拆解多目标优化的核心玩法。

权重加权法就像把奶茶里的珍珠和椰果按比例搅成糊状，简单但容易翻车。假设我们要优化两个函数f1和f2，代码可以这样写：

python 复制代码

def weighted_sum(x):
    return 0.6 * f1(x) + 0.4 * f2(x)
    
result = minimize(weighted_sum, x0)

但这样粗暴的加权会漏掉关键解------就像选择困难症患者把红蓝药丸都吞了。真正的多目标解法应该像超市货架一样展示所有可能选项，这就是Pareto解的奥义。

上硬货！用Python的pymoo库实现NSGA-II算法。先定义个双目标优化问题：

python 复制代码

from pymoo.core.problem import ElementwiseProblem

class MyProblem(ElementwiseProblem):
    def __init__(self):
        super().__init__(n_var=2, n_obj=2, n_constr=0)
        
    def _evaluate(self, x, out, *args, **kwargs):
        f1 = (x[0]-2)**2 + (x[1]-1)**2
        f2 = (x[0]+2)**2 + (x[1]+3)**2
        out["F"] = [f1, f2]

这里定义了两个互相拉扯的目标函数：f1要求解靠近(2,1)，f2要求靠近(-2,-3)。运行NSGA-II：

python 复制代码

from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.optimize import minimize

algorithm = NSGA2(pop_size=100)
res = minimize(MyProblem(), algorithm, ('n_gen', 50))

关键参数popsize控制解的多样性，ngen是迭代次数。把结果可视化：

python 复制代码

import matplotlib.pyplot as plt

F = res.F
plt.scatter(F[:,0], F[:,1], s=30, edgecolors='k')
plt.xlabel('目标1', fontsize=12)
plt.ylabel('目标2', fontsize=12)
plt.show()

得到的散点图就是传说中的Pareto前沿，每个点代表一个最优折中方案。这时候产品经理可以按需选择------要极致性能就选左边的点，追求续航就挑右边的。

对比下PSO和遗传算法的效果差异。PSO实现需要稍作修改：

python 复制代码

from pymoo.algorithms.so_pso import PSO

algorithm = PSO(pop_size=50)
res_pso = minimize(MyProblem(), algorithm, ('n_gen', 100))

实际测试发现NSGA-II在解集分布均匀性上更胜一筹，而PSO有时会出现解集聚集现象。这就像猎豹擅长短跑，骆驼适合沙漠------算法选择要看具体战场。

实战中有三个避坑指南：

目标归一化很重要，别让量纲差异毁了优化结果
约束条件处理要巧妙，试试罚函数法
高维问题记得用超体积指标评估解集质量

最后留个思考题：当目标函数计算耗时太长时，怎么加速Pareto前沿搜索？答案是代理模型+迁移学习的组合拳，不过这得留到下回分解了。记住，多目标优化不是寻找唯一真理，而是绘制完整的可能性地图------这才是智能决策的终极形态。