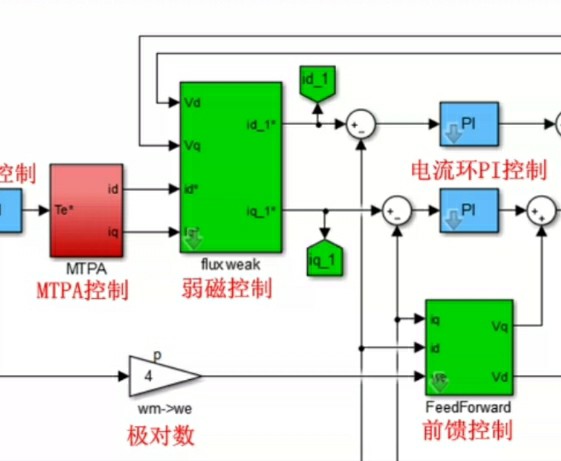
SIMULINK/MATLAB仿真内嵌式永磁同步电机弱磁控制：从MTPA到前馈弱磁

SIMULINK/MATLAB仿真内嵌式永磁同步电机弱磁控制；前馈弱磁最大转矩电流比控制mtpa MTPA有详细文档讲解

在电机控制领域，内嵌式永磁同步电机（IPMSM）凭借其高效、高功率密度等优点得到广泛应用。而弱磁控制则是拓展其运行范围的关键技术。今天咱们就来聊聊基于SIMULINK/MATLAB平台的IPMSM弱磁控制，特别是前馈弱磁和最大转矩电流比控制（MTPA）。

MTPA控制

MTPA控制是实现电机高效运行的重要策略。简单来说，它的目标就是在给定转矩的情况下，使定子电流最小，从而降低铜耗，提高电机效率。

我们可以通过数学推导来确定MTPA轨迹。对于IPMSM，转矩方程为：

\[Te = 1.5 p \left[\psi f iq + (L d - Lq) id i_q\right]\]

其中，\(p\)是极对数，\(\psif\)是永磁体磁链，\(L d\)、\(Lq\)分别是\(d\)、\(q\)轴电感，\(id\)、\(i_q\)分别是\(d\)、\(q\)轴电流。

为了实现MTPA，我们要找到一个\(id\)和\(iq\)的关系，使得在特定转矩下电流最小。通过对转矩方程求导等一系列操作（具体推导过程可参考详细文档讲解），我们可以得到MTPA曲线。

在MATLAB代码中，可以这样简单实现MTPA的查找：

matlab 复制代码

% 假设已经有转矩Te的范围
Te_range = 0:0.1:10; % 转矩范围从0到10 Nm，步长0.1 Nm
psi_f = 0.1; % 永磁体磁链
L_d = 0.01; % d轴电感
L_q = 0.03; % q轴电感
p = 4; % 极对数

for i = 1:length(Te_range)
    Te = Te_range(i);
    % 根据MTPA关系计算id和iq
    iq = sqrt((Te / (1.5 * p * psi_f))^2 + (Te / (1.5 * p * (L_d - L_q)))^2) - (Te / (1.5 * p * psi_f));
    id = -iq * (L_d - L_q) / psi_f;
    MTPA_id(i) = id;
    MTPA_iq(i) = iq;
end

这段代码通过给定的转矩范围，根据MTPA的数学关系计算出对应的\(id\)和\(iq\)值。实际应用中，我们可以把这些值存储在查找表中，实时根据转矩需求获取合适的电流值。

前馈弱磁控制

随着电机转速升高，反电动势也会增大，超过逆变器所能提供的电压极限时，就需要弱磁控制来拓展转速范围。前馈弱磁控制就是一种有效的方法。

前馈弱磁控制主要通过对\(d\)轴电流进行控制，使电机的磁链减小，从而降低反电动势。在MATLAB/SIMULINK仿真中，我们可以这样搭建模型。

首先，在电机模型的基础上，添加一个弱磁控制模块。该模块根据当前转速和电压极限来计算需要的\(d\)轴弱磁电流。

matlab 复制代码

% 假设已经有当前转速omega和电压极限V_limit
omega = 1000; % 转速 1000 rad/s
V_limit = 300; % 电压极限 300V

% 计算弱磁前馈电流
psi_f = 0.1;
L_d = 0.01;
L_q = 0.03;
R_s = 0.5; % 定子电阻

% 估算反电动势
E = omega * psi_f;
% 计算需要的d轴弱磁电流
id_weak = (V_limit - sqrt((R_s * iq)^2 + (omega * L_q * iq)^2)) / (omega * L_d);

这段代码根据当前转速计算反电动势，再结合电压极限和电机参数计算出需要的\(d\)轴弱磁电流。

在SIMULINK中，我们可以把这些计算逻辑封装成一个子系统，然后与电机模型、MTPA模块等连接起来。通过这种方式，就能实现IPMSM从MTPA控制到弱磁控制的平滑过渡，在不同转速下都能高效运行。

通过在MATLAB/SIMULINK中对IPMSM的弱磁控制进行仿真研究，我们可以深入理解前馈弱磁和MTPA控制的原理与实现方式，为实际电机控制系统的设计提供有力的参考。