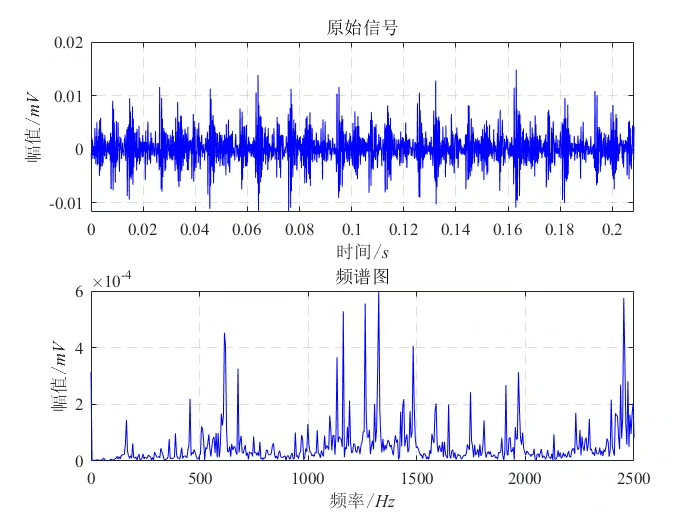
信号去噪算法：VMD、优化VMD、WD及多模型混合的Matlab实践

基于变分模态分解算法(VMD)、优化VMD算法、小波阈值去噪(WD)以及多模型混合的信号去噪算法 Matlab语言实现，代码质量极高，方便学习和替换数据。

在信号处理领域，去噪是一项至关重要的任务，它能让我们从嘈杂的数据中提取出真正有用的信息。今天咱们就来聊聊基于变分模态分解算法（VMD）、优化VMD算法、小波阈值去噪（WD）以及多模型混合的信号去噪算法，并且看看如何用Matlab来实现这些超酷的算法。

变分模态分解算法（VMD）

VMD是一种自适应的信号分解方法，它将复杂信号分解为一系列具有不同中心频率的固有模态函数（IMF）。

先来看段简单的Matlab代码实现VMD的核心部分：

matlab 复制代码

% 参数设置
alpha = 2000; % 二次惩罚因子
tau = 0; % 噪声容限（设为0表示无噪声）
K = 3; % 分解模态数
DC = 0; % 直流分量设置
init = 1; % 初始化模式选择
tol = 1e-7; % 收敛精度

% 假设已有含噪信号x
% 调用VMD函数
[u, u_hat, omega] = VMD(x, alpha, tau, K, DC, init, tol);

这里呢，alpha 决定了频域带宽惩罚的程度，数值大的话，IMF的带宽会被约束得更窄；tau 如果不为0，可以允许一定噪声存在；K 就是我们想把信号分解成几个模态，这个值得根据信号的特性来调；DC 控制是否移除直流分量；init 选择初始化方式；tol 是迭代收敛的精度，数值越小收敛要求越高。

优化VMD算法

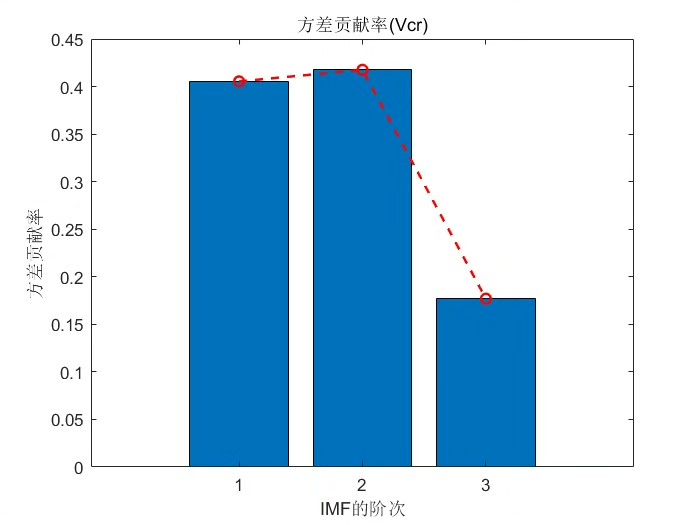
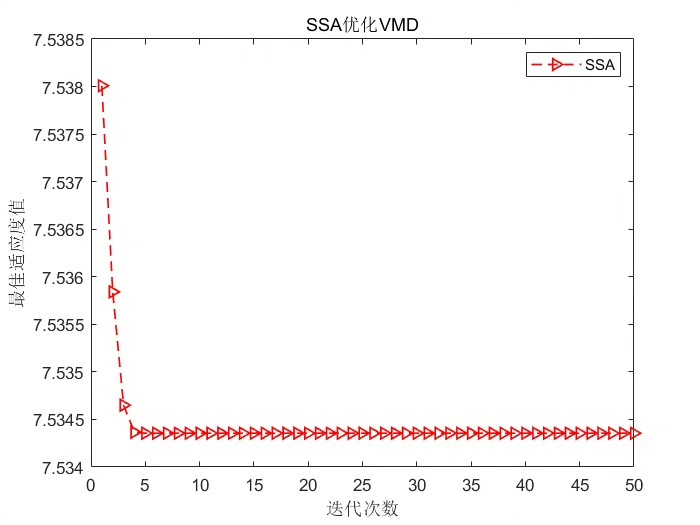
优化VMD算法通常是在原始VMD基础上对参数选择、分解过程等进行改进，以更好地适应特定信号的去噪需求。比如可能通过智能算法去寻找最优的 K 值。

matlab 复制代码

% 这里假设使用遗传算法来优化K值
function [bestK] = optimizeK(x)
    % 遗传算法参数设置
    nvars = 1; % 变量数，这里就是K
    lb = 2; % K的下限
    ub = 10; % K的上限
    fitnessFcn = @(k) evaluateVMD(x, k); % 适应度函数，这里根据VMD结果评估
    options = gaoptimset('PopulationSize',50,'Generations',100);
    [bestK, ~] = ga(fitnessFcn, nvars, [], [], [], [], lb, ub, [], options);
end

function fitness = evaluateVMD(x, k)
    alpha = 2000; 
    tau = 0; 
    DC = 0; 
    init = 1; 
    tol = 1e-7; 
    [u, ~, ~] = VMD(x, alpha, tau, k, DC, init, tol);
    % 这里可以根据分解后IMF的一些特性来定义适应度，比如IMF能量分布合理性等
    % 简单示例：假设IMF能量越均匀，适应度越高
    energy = sum(u.^2, 1);
    fitness = -var(energy); % 负方差，因为希望方差小（能量均匀）
end

在这个优化代码里，我们用遗传算法去搜索 K 的最优值。optimizeK 函数设置了遗传算法的参数，包括变量范围、种群大小、迭代代数等，然后调用遗传算法 ga 去寻找最优 K。evaluateVMD 函数是适应度评估函数，这里简单根据分解后IMF的能量方差来评估，方差越小说明能量分布越均匀，适应度越高，当然实际应用可以根据信号特点设计更复杂合理的评估方式。

小波阈值去噪（WD）

小波阈值去噪基于小波变换，把信号分解到不同尺度的小波系数上，然后通过阈值处理来去除噪声相关的系数。

matlab 复制代码

% 假设已有含噪信号x
wname = 'db4'; % 小波基选择，这里选db4
level = 5; % 分解层数
% 小波分解
[c, l] = wavedec(x, level, wname);
% 计算阈值
thr = wthrmngr('dw1ddenoLVL', 'mln', c, l);
% 软阈值处理
s = wthresh(c, 's', thr);
% 小波重构
denoised_x = waverec(s, l, wname);

这里先选了 db4 小波基，不同的小波基对信号的分析特性不一样，得根据信号特点选。level 是分解层数，层数越多对信号细节分析越精细，但计算量也越大。通过 wavedec 进行小波分解得到系数 c 和长度向量 l ，然后用 wthrmngr 计算阈值，这里用的是一种基于最小极大准则的阈值计算方法。接着用软阈值函数 wthresh 处理系数，最后通过 waverec 重构出去噪后的信号。

多模型混合的信号去噪算法

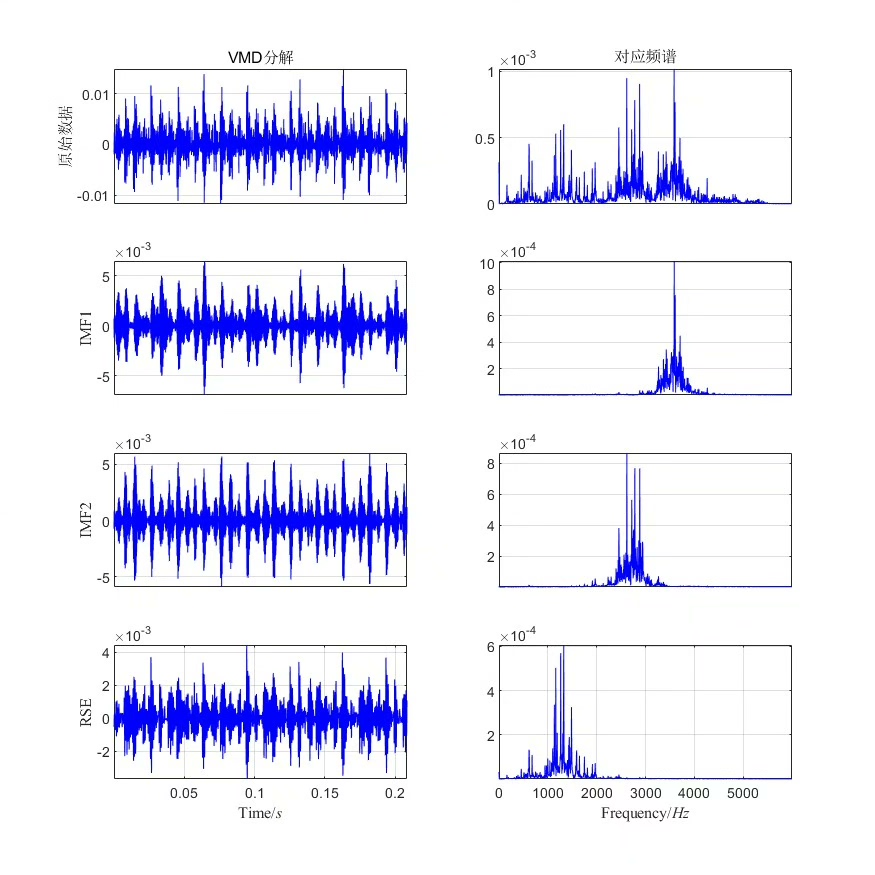
多模型混合可以结合上述算法的优点。比如先用VMD把信号分解，对每个IMF再用小波阈值去噪，然后重构。

matlab 复制代码

% 假设已有含噪信号x
% VMD分解
alpha = 2000; 
tau = 0; 
K = 3; 
DC = 0; 
init = 1; 
tol = 1e-7; 
[u, ~, ~] = VMD(x, alpha, tau, K, DC, init, tol);

denoised_u = zeros(size(u));
wname = 'db4'; 
level = 5; 
for i = 1:K
    % 对每个IMF进行小波阈值去噪
    [c, l] = wavedec(u(:, i), level, wname);
    thr = wthrmngr('dw1ddenoLVL', 'mln', c, l);
    s = wthresh(c, 's', thr);
    denoised_u(:, i) = waverec(s, l, wname);
end

% 重构去噪后的信号
denoised_x = sum(denoised_u, 2);

这段代码先进行VMD分解，得到各个IMF，然后对每个IMF都进行小波阈值去噪，最后把去噪后的IMF叠加起来重构出最终去噪后的信号。这种混合方式充分利用了VMD的自适应分解特性和小波阈值去噪在细节处理上的优势，往往能取得比单一算法更好的去噪效果。

通过这些算法的Matlab实现，无论是学习信号处理知识，还是在实际项目中替换数据进行信号去噪应用，都非常方便，希望大家能在自己的信号处理工作中灵活运用这些方法。