三自由度汽车操纵侧翻模型仿真 有说明文档 学习资料:附带整理好的Word理论分析说明文档,方便学习 ①基于二自由度模型的成熟理论,采用SAE坐标系建立三自由度汽车操纵模型。 ②该模型结构较为简单,能够反映出车辆侧向、横摆及侧倾运动的基本特征,适用于稳定性控制系统研究。 ③仿真结果:在对模型的操纵特性进行分析时可以看出本文所搭建模型可以较好的反映出汽车车身侧倾状态,而且汽车转弯行驶时随着车速的提高,汽车车身侧倾越严重

深夜调完最后一个参数,盯着屏幕上那条逐渐收敛的曲线,突然想起实验室师兄说过的话:"车辆侧倾就像奶茶杯里的珍珠,晃得越厉害,撒出来的风险就越大。"今天要聊的三自由度汽车侧翻模型,本质上就是在用数学公式计算这杯"奶茶"什么时候会洒。
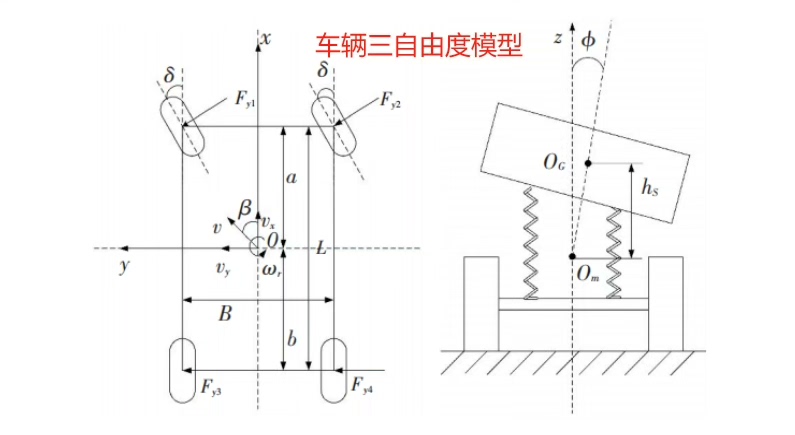
先看模型核心------把车拆解成三个方向的运动。二自由度模型大家都熟,横摆和侧向两个维度像在冰面上画八字。但真实开车时身体能感受到的左右倾斜,就藏在新增的第三个自由度里:侧倾运动。代码里用phi表示的这个角度,直接关系到车辆翻不翻车的关键时刻。
python
def vehicle_dynamics(t, states):
beta, r, phi, p = states # 侧偏角、横摆角速度、侧倾角、侧倾角速度
delta = steer_input(t) # 前轮转角输入
# 轮胎侧向力计算
Fyf = Cf * (delta - beta - a*r/U)
Fyr = Cr * (-beta + b*r/U)
# 侧倾力矩计算
M_phi = (m_s * h * U**2 * r) - (K_phi * phi) - (C_phi * p)
# 构建微分方程组
dbeta = (Fyf + Fyr)/(m*U) - r
dr = (a*Fyf - b*Fyr)/Izz
dphi = p
dp = (M_phi - m_s*h*U*dbeta)/Ixx
return [dbeta, dr, dphi, dp]这段代码藏着三个彩蛋:1)轮胎模型用了线性假设,就像用直线段拼接弯道;2)侧倾惯性矩Ixx的计算需要知道车身质量分布,这参数实测比仿真难十倍;3)m_s*h这个组合参数是侧翻的定时炸弹------坐满人的SUV和空载的跑车在这里会走出完全不同的命运轨迹。
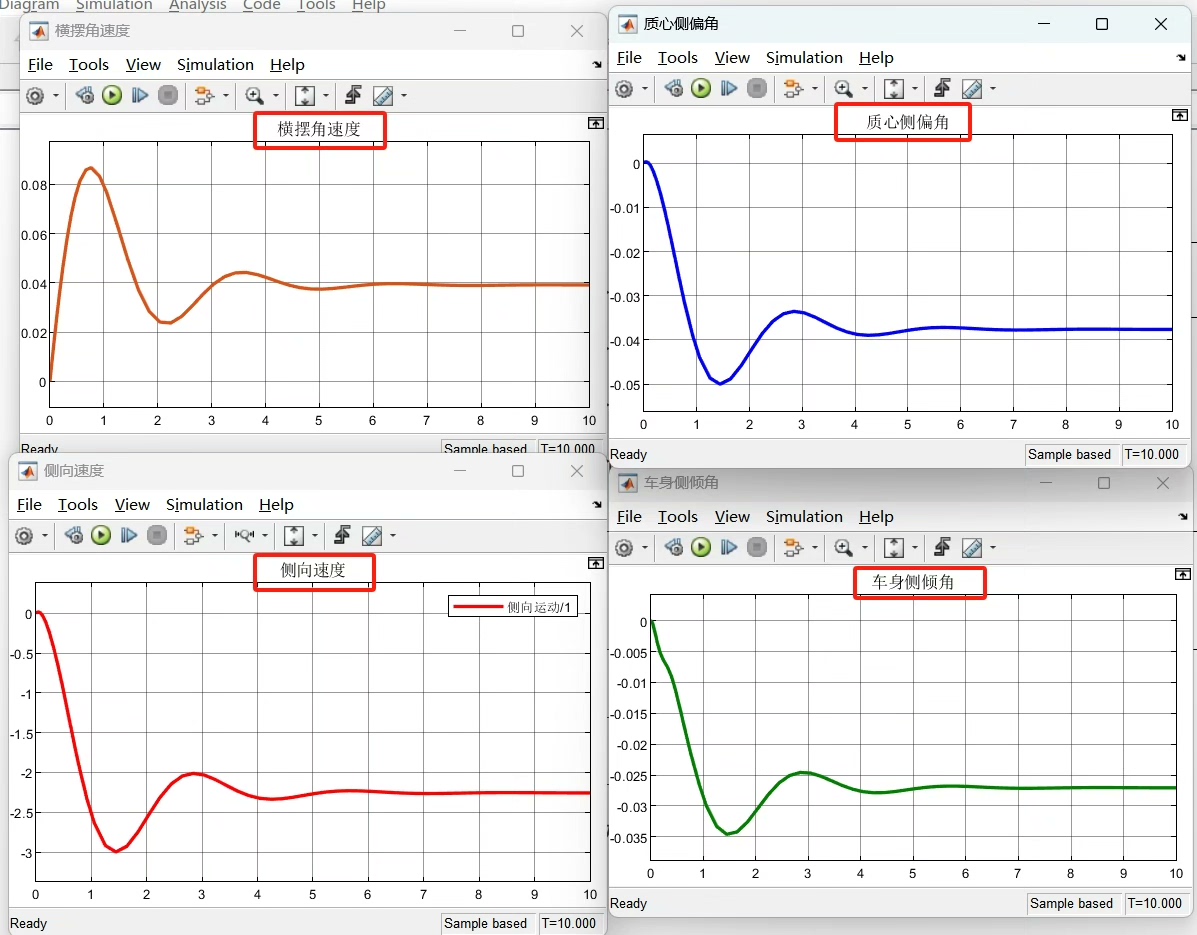
跑个急转弯工况试试看。设定车速从60km/h逐步提升,方向盘转角保持60度不变。当代码中的U参数突破某个临界值时,phi曲线就像坐上了火箭:
python
# 仿真参数设置
U = np.linspace(60, 100, 5) # 车速从60到100km/h分五档测试
steer_angle = 60 * np.pi/180 # 60度转向角转弧度
for speed in U:
sol = solve_ivp(vehicle_dynamics, [0, 10],
[0, 0, 0, 0], args=(speed,))
plt.plot(sol.t, sol.y[2], label=f'{speed}km/h')跑出来的图像特别有意思------60km/h时侧倾角像温顺的猫,80km/h变成躁动的二哈,到100km/h直接化身暴走的哥斯拉。这说明模型成功捕捉到了"速度是侧翻帮凶"的物理本质。但要注意,这里没考虑悬架的非线性特性,真实情况可能在临界点前就会出现轮胎离地的突变。
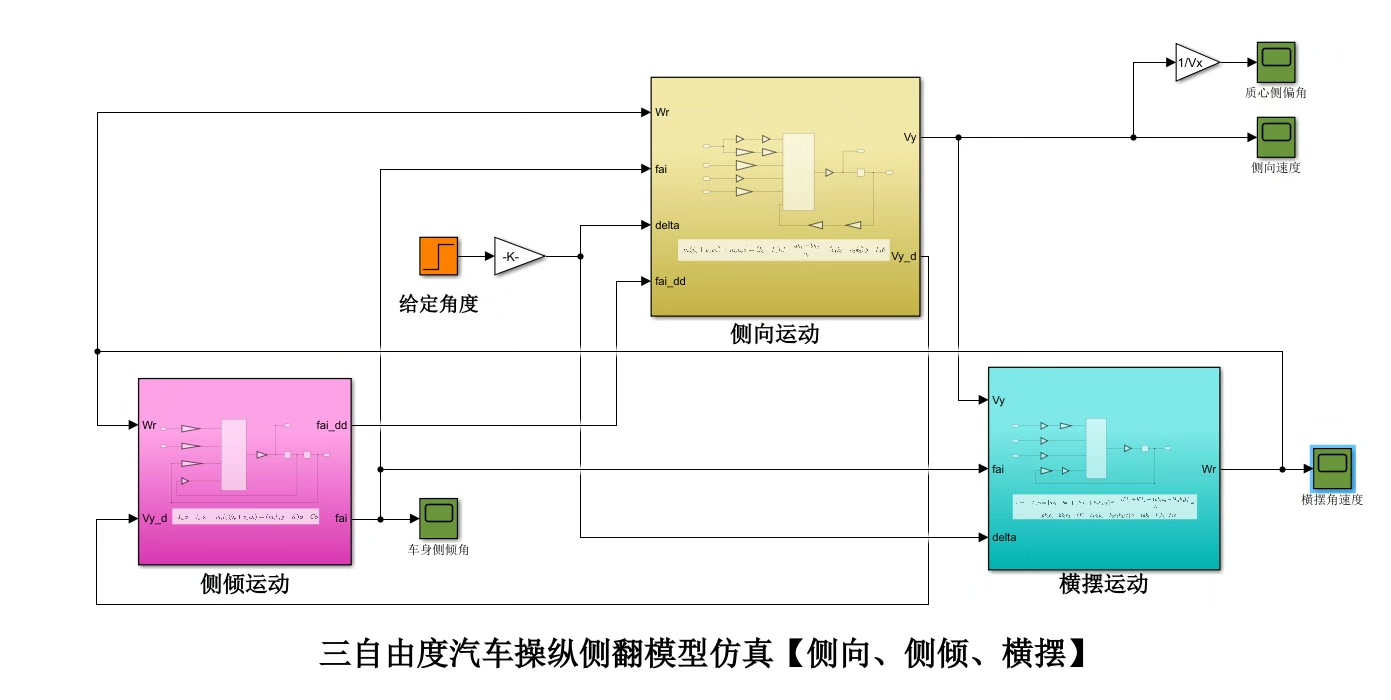
模型验证时有个反直觉现象:降低悬架刚度K_phi反而可能提升稳定性。因为柔软的悬架允许更大侧倾角,相当于给侧倾能量开了个泄洪口。但这是双刃剑,就像蹦极绳太松反而危险,需要结合ESC控制策略来动态调节。
凌晨三点保存仿真数据时突然顿悟:所谓车辆稳定性控制,本质上是在侧倾角速度和横摆角速度之间走钢丝。下次试试把ESP控制逻辑接入这个模型,看能不能在奶茶杯将倾未倾的瞬间,用制动干预上演一场力挽狂澜的好戏。