关于脑动态网络研究的一些方法和论文

在写作搜集资料的过程中发现了已有的一些介绍：

高度相关文章1从静息态和任务态大数据中探索动态脑网络 blog

原始文献 从静息态和任务态的大数据中发现动态脑网络 Discovering dynamic brain networks from big data in rest and task

使用fMRI数据提取大脑功能网络方法综述A survey of brain functional network extraction methods using fMRI data

本文只构建一个对于这个研究方向的图景，而不专注某个方法和细节是如何实现的。

关于大脑状态的定义，划分，状态转移，我认为是一个非常有趣的问题和研究对象。

作为一个无监督学习的过程，考虑到脑数据获取的难度和状态定义的复杂性，这个领域的发展和研究相对缓慢，但也具备了一定的研究成果。

为了对分析的对象进行聚焦，很理所当然的，我们首先选择的方式是滑动窗口。

滑动窗口，cap(共激活模式)，HHM是主流的三大方法。

滑动窗口，将生理信号切片为固定长度的大小，切割了

但是最新的研究也提出了复杂性相对较高的一些方法。

生成式模型是相对比较热门的一个方向，如果模型可以捕捉信号的特征，使用数据驱动的方式重新生成，那么我们就可以从模型的识别模式中，去分解关键的类型和判定区别的依据。从潜空间进行模式分析。

因此VAE和其变体也非常具备分析和应用的价值，且在fmri和eeg，meg上都有相应的尝试。

常用的数据大概有fmri，eeg和meg。

由于时间分辨率的原因。对于fmri，现有的yeo的多种模式网络的划分是具备较多认可的。

而eeg和meg这些作为时间分辨率高，但是空间定位深度相对不足的，一般是参考该信号和模式来继续验证性的研究。

MEG作为一个时间和空间分辨率都较高的数据，通过溯源后，研究脑皮层的模式转换是常见是数据选择，可以填补脑的活动模式在毫秒级别的研究。

历史上已经有相关文献提出了这种现象并进行了研究。

关于动态网络的研究。最新的一个研究脉络，我简单归纳认为有三种较有潜力的方法。还有一种通过vqvae来进行生成和研究的内容。现在很多内容还处于预印本，未发表的状态。

meg背景的文章

在MEG的头皮溯源数据上进行了相关验证。如下面这篇文章

自发人类脑活动中快速瞬时网络
Fast transient networks in spontaneous human brain activity

DOI: http://dx.doi.org/10.7554/eLife.01867.001

2014 Mar 25;

Spontaneous cortical activity transiently organises into frequency specific phase-coupling networks
自发性皮层活动会短暂地组织成频率特异性的相位耦合网络

30 July 2018

使用的meg，HMM的分析方法，此外，使用的是42个覆盖全脑区域的模板，研究的是dmn和相关的静息态网络的一些子部分。

预测性大脑的秘密生活：自发活动有何作用？
The secret life of predictive brains: what's spontaneous activity for?

2021 Jun 16;25(9):730--743. doi: 10.1016/j.tics.2021.05.007

tvdn 时变动态网络模型

时变动态网络模型：用于 fMRI 和 MEG 成像的动态静息态功能连接tvdn
Time-varying dynamic network model for dynamic resting state functional connectivity in fMRI and MEG imaging

2022 年 7 月 1 日

数学和流形的角度，计算相对复杂。

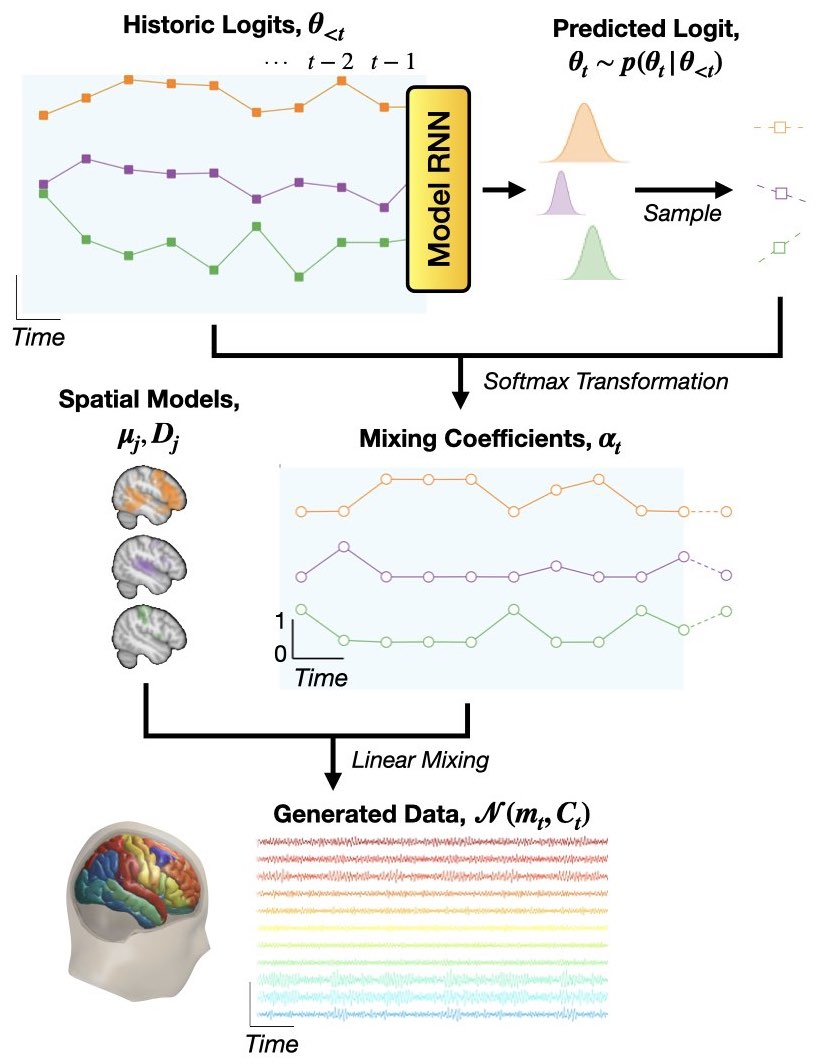
DyNeMo 动态功能脑网络

大规模动态功能脑网络模式的混合DyNeMo
Mixtures of large-scale dynamic functional brain network modes

2022 年 11 月

引入深度学习时序的网络来进行统计建模。

说明和下载文档

从文档中可以看到，这个模型实际上使用了RNN和lstm的时序建模。，改进了HMM的建模模式。

如果下载使用的时候，其使用的是tensorflow的环境。

VAE的引入和两篇较新的文章

可以参考这些文章的参考文献，研究vae在这个领域的发展。

基于扩散驱动的脑网络功能磁共振成像连接增强技术用于提高自闭症谱系障碍的诊断准确性

本文使用了vqvae的思想，构造的是fc连接的VQ量化层。

MEG的大型transform模型结构，此文章还进行了一些子任务的功能验证。
MEG-GPT: A transformer-based foundation model for magnetoencephalography data

在大规模 MEG 数据集（N=612，闭眼静息，Cam-CAN 数据）中提取的标记化脑区时间序列上训练了 MEG-GPT

在arXiv的版本中，没有每个部分的详细说明，但是在pdf版本中，有数据处理相关的方法说明。和模型结构参数的解析。

使用的是lcmv波束形成溯源，然后使用的分区模板是glasser52，专用于meg的分析的分区，是2023年提出的，根据HCP-MMP 图谱，22 个区域对健康对照组和帕金森病患者 MEG 记录的影响，在此基础上进行了分割。

此外这个文章附带了gituhb仓库，主要的结构有base，meg-gpt和tokenizer三个部分。github地址

在时序和编码中采用了无损表示的方式。

HHM和tvdn时变动态网络，算法动态网络模式（DyNeMo）。

这三种是提出的较为主流的研究方式。

此前的如脑网络模式的提出，主要使用k-means的思想和方法。

这个聚类的相关方法，在脑的微状态也具备高度的同源性。

因此更深层级，更小时间尺度的状态分割研究，可以从传统方法寻找依据和革新。

下面我先用ai来介绍和对比一下这几个方法。

我来帮你梳理这几种脑网络动态分析算法的发展脉络和核心思想。

HHM的发展

年份	一句话故事	金句/彩蛋	文献
2013	Eavani 把 fMRI 塞进 HMM，第一次让"全脑网络"变成可数的离散状态。	"原来秒级的慢舞，也能被切成一帧一帧。"	Unsupervised learning of functional network dynamics in resting state fMRI
2014	Baker 用 MEG 给 HMM 按下快进键，发现静息态网络 100 ms 就换一次"镜头"。	"fMRI 眼里的慢动作，在 MEG 里全是快闪。"	Fast transient networks in spontaneous human brain activity
2015	Time-Varying Effective Connectivity for Describing the Dynamic Brain Networks of Post-stroke Rehabilitation时变有效连接性：描述中风康复的动态脑网络	开始在一些疾病的发展的角度应用并分析网络模式	时变有效连接性：描述中风康复的动态脑网络
2016	Vidaurre 把任务态也拉下水------不告诉你任务是什么，HMM 自己猜出实验设计。	"无监督学习也能复现刺激时间表，比实验员还准时。" 强调功能连接而非振幅的变化 Time Varying Networks 时变网络	Spectrally resolved fast transient brain states in electrophysiological data
2017	小组件时代：HMM 开始被塞进 PTSD、癫痫、阿尔茨海默的临床工具箱。	未找到相关内容，可能是ai幻觉，但是后续有一个整合的工具箱	OHBA工具箱
2018	随机变分推断上线，单机可吞 820 HCP + 5 248 UK Biobank 被试。	"大数据的门槛，从'买不起服务器'降到'笔记本也能跑'。"	工具python版本 matlab版本来自Discovering dynamic brain networks from big data in rest and task
2019	Hidden Semi-Markov Model（HSMM）补刀：停留时间不再被几何分布绑架。	"终于可以理直气壮地说'这个状态持续了 300 ms'，而不是'平均 250±∞'。"	使用隐藏半马尔可夫模型改进动态功能连接中的状态变化估计
2022	DyNeMo 登场，状态不再互斥，重叠网络成为新常态。	"大脑不是幻灯片，而是 Photoshop 图层。"	Mixtures of large-scale dynamic functional brain network modes
2023	TDE-HMM 把 TMS-EEG 也收入囊中，实现"状态依赖"神经调控。	"在正确的时间戳一下，比乱戳十下更有效。"	原文工具函数
2024	社区共识：HMM 成为"动态功能连接"三大支柱之一（另俩是滑动窗与 CAP）。	"从'小众模型'到'标配工具'，只差十年。"	OHBA工具箱

Hidden Semi-Markov Model（HSMM）

HSMM论文:

HSMM应用于脑网络的开创性论文

Shappell et al., 2019 - 脑网络HSMM的奠基之作

论文标题 : "Improved state change estimation in dynamic functional connectivity using hidden semi-Markov models"
发表 : NeuroImage, 2019年5月1日 (Volume 191, Pages 243-257)
在线发表 : 2019年2月10日
DOI: 10.1016/j.neuroimage.2019.02.013

作者团队:

Heather Shappell (第一作者,约翰霍普金斯大学生物统计系)
Brian S. Caffo (约翰霍普金斯大学生物统计系)
James J. Pekar (Kennedy Krieger研究所和约翰霍普金斯医学院)
Martin A. Lindquist (通讯作者,约翰霍普金斯大学生物统计系)

核心问题与创新

HMM的根本局限:

HMM假设停留时间(sojourn time,即在某个状态连续停留的时间点数)服从几何分布,这可能导致对状态切换前停留时间的不准确估计

几何分布的问题:

复制代码

几何分布特性:
P(停留时间 = t) = (1-p)^(t-1) * p

问题1: 单调递减 - 停留1个时间点的概率最高
问题2: 无记忆性 - 不考虑已经停留多久
问题3: 所有状态共享相似模式

实际脑状态:
- 任务实验中,被试可能在某状态停留数分钟
- 不同状态应有不同的停留时间模式

HSMM的解决方案:

HSMM显式地将停留分布(sojourn distribution)构建到似然函数中,可以指定分布采用非参数形式或参数形式(如泊松分布或伽马分布),直接估计参数

方法学核心

1. 模型对比

特征	HMM	HSMM
状态过程	马尔可夫链	半马尔可夫链
停留时间	几何分布(隐式)	任意分布(显式建模)
转移概率	每步都可能转移	条件转移概率(给定离开当前状态)
参数	转移矩阵P	停留分布d + 条件转移矩阵Ω

2. HSMM数学框架

状态表征:

每个状态k有独特的:
- 均值向量 μₖ (各ROI的平均激活)
- 协方差矩阵 Σₖ (功能连接模式)
- 停留分布 dₖ(t) (停留时间的概率分布)

观察模型 :
Y t ∣ S t = k N ( μ k , Σ k ) Y_t | S_t=k ~ N(μₖ, Σₖ) Yt∣St=k N(μk,Σk)

停留分布选择:

非参数: 直接估计离散概率质量函数
泊松分布 : d k ( t ) = P o i s s o n ( λ k ) d_k(t) = Poisson(λₖ) dk(t)=Poisson(λk)
伽马分布 : d k ( t ) = G a m m a ( α k , β k ) d_k(t) = Gamma(α_k, β_k) dk(t)=Gamma(αk,βk)

实验验证

仿真研究 (Simulation Study)

对三个模拟数据集进行了仿真,第一个包含较长状态停留时间和较大信噪比,第二个有相同长的停留时间但较小信噪比,第三个有短停留时间和大信噪比

关键发现:

HSMM在所有场景下都更准确地估计停留时间分布
当真实停留时间为泊松分布时,HMM系统性地低估停留时间
HSMM估计的网络状态与真实状态高度一致

真实数据分析

数据1: 焦虑诱导任务态fMRI

实验设计:被试观看诱发焦虑的视频片段
结果:HSMM能识别与焦虑相关的特定脑状态及其停留模式

数据2: HCP静息态fMRI

使用Human Connectome Project的静息态fMRI数据进行分析

主要发现:

识别出12个可重复的脑网络状态
不同状态的停留时间分布显著不同
停留时间与持续注意力评分相关

核心贡献

1. 方法学创新

提出使用HSMM寻找每个被试最可能的网络状态序列和每个状态关联的图,同时正确估计和建模每个状态的停留分布

技术实现:

使用Viterbi算法推断最可能的状态序列
EM算法估计模型参数
支持多被试联合建模

2. 停留时间的神经科学意义

研究发现:

停留时间模式可能反映:
- 认知控制能力
- 网络稳定性
- 个体差异特征

结果展示了模型选择在估计停留时间时的重要性,揭示了其理解健康和疾病脑机制的潜力

3. 与传统方法的比较

验证了该方法并与几种常见现有方法(如滑动窗口分析和标准HMM)进行比较

性能对比:

复制代码

准确性排名(停留时间估计):
HSMM > HMM >> 滑动窗口

状态估计:
HSMM ≈ HMM > 滑动窗口

解释性:
HSMM > HMM (提供显式停留分布)

后续影响与应用

广泛采用 (2019-2025)

HSMM已应用于NCANDA青少年酒精消费研究,使用三网络(默认模式、突显和中央执行网络)建模

应用于老年肥胖人群的食物线索任务研究,分析减重意向与脑网络动态的关系

2025年1月的最新研究使用HSMM分析特质冲动性和焦虑的时变脑状态动态

软件工具

Shappell等人(2019, 2021)使用R语言的mhsmm包进行fMRI动态连接分析

Naturalistic Data Analysis项目提供了详细的HSMM教程,包括R代码实现

方法学扩展

当前正在开发两个扩展:(1)混合效应HSMM模型用于估计个体和群体脑网络动态,同时控制潜在混淆变量;(2)允许协变量预测停留时间的HSMM实现

与其他动态方法的关系

发展脉络:

复制代码

2013-2014: HMM引入脑网络
    ↓
2019: HSMM改进停留时间建模 ← 你问的这篇
    ↓
2021: HSMM协变量扩展
    ↓
2022: DyNeMo (允许状态共存)
    ↓
2024: 多尺度动态建模

HSMM vs DyNeMo:

维度	HSMM	DyNeMo
状态性质	互斥	可重叠混合
停留时间	显式建模	隐式(通过RNN)
优势	停留时间更准确	捕捉状态共存
适用场景	清晰状态切换	复杂模式叠加

实践建议

如果你想使用HSMM:

1. 选择停留分布

R 复制代码

# 泊松分布(最常用)
sojourn = "poisson"

# 伽马分布(更灵活)
sojourn = "gamma"  

# 非参数(完全自由)
sojourn = "nonparametric"

2. 确定状态数

状态数必须提前确定,受时间序列长度、被试数和ROI数等因素强烈影响
建议:从小到大尝试(3-12个状态)
使用BIC/AIC选择

3. R实现

R 复制代码

library(mhsmm)

# 定义初始参数
J = 12  # 状态数
init = list(
  J = J,
  initial = rep(1/J, J),  # 初始状态概率
  P = ...,                 # 转移概率
  sojourn = "poisson",     # 停留分布
  lambda = ...,            # 泊松参数
  mu = ...,               # 均值
  sigma = ...             # 协方差
)

# 拟合模型
model = mhsmm.fit(data, init)

方法的讨论

发展历程概览

这些算法代表了静态 → 动态 → 时变动态的演进过程:

1. HMM (Hidden Markov Model) - 隐马尔可夫模型

时间 : 最早应用于脑网络分析
核心思想:

假设大脑在离散的、有限个状态之间切换
每个状态对应一种稳定的功能网络配置
状态转换遵循马尔可夫过程(当前状态只依赖前一状态)
局限: 假设每个时刻大脑只处于一个单一状态

典型特征:

硬分割(hard segmentation):每个时间点只属于一个状态
离散状态空间
状态持续时间较长且稳定

2. DyNeMo (Dynamic Network Modes, 2022)

核心创新:

多状态共存 : 允许多个网络模式同时激活
从"状态切换"到"模式混合"的范式转变

关键思想:

复制代码

传统HMM: 时刻t → 状态A (100%)
DyNeMo:  时刻t → 状态A(60%) + 状态B(30%) + 状态C(10%)

技术特点:

使用variational Bayes推断
每个时间点的网络是多个"纯净模式"的加权组合
权重系数是时变的,反映各模式的激活强度
软分割(soft segmentation)

3. M-DyNeMo (Multiscale DyNeMo)

发展方向 : 在DyNeMo基础上引入多时间尺度

核心思想:

不同脑网络模式在不同时间尺度上演变
快速模式: 毫秒-秒级(如感知觉处理)
慢速模式: 秒-分钟级(如注意力维持)

创新点:

分层建模不同频率的动态变化
捕捉跨尺度的交互作用
更符合大脑多层级时间组织的神经生理现实

4. TvDN (Time-varying Dynamic Networks)

核心特点 : 连续时变而非状态切换

思想转变:

复制代码

HMM/DyNeMo: 离散模式 + 组合
TvDN:       连续演化的网络拓扑

方法学特征:

使用滑动窗口或贝叶斯平滑技术
网络连接强度连续变化(无需预定义状态)
可能结合稀疏性约束保证可解释性

优势:

不假设存在固定数量的状态
更灵活地捕捉渐变过程
适合分析平滑过渡的脑活动(如学习、疲劳累积)

思想演进的核心脉络

认知转变:

单一状态 (HMM)
→ 2. 多状态共存 (DyNeMo)
→ 3. 多尺度共存 (M-DyNeMo)
→ 4. 连续演化 (TvDN)

数学表达:

HMM: s t ∈ { 1 , 2 , . . . , K } s_t \in \{1,2,...,K\} st∈{1,2,...,K} (离散状态)
DyNeMo: w t = [ w t , 1 , . . . , w t , K ] \mathbf{w}t = [w{t,1}, ..., w_{t,K}] wt=[wt,1,...,wt,K] , ∑ w t , k = 1 \sum w_{t,k}=1 ∑wt,k=1 (概率分布)
M-DyNeMo: w t f a s t , w t s l o w \mathbf{w}_t^{fast}, \mathbf{w}_t^{slow} wtfast,wtslow (多尺度权重)
TvDN: A ( t ) \mathbf{A}(t) A(t) (连续时变邻接矩阵)

实际应用考量

算法	适用场景	主要假设
HMM	任务切换明确的实验	状态离散且互斥
DyNeMo	复杂认知任务、静息态	模式可叠加
M-DyNeMo	需要多尺度分析的数据	存在层级时间结构
TvDN	学习过程、发育研究	平滑渐变过程

关键问题

这些算法各有优劣,选择时需考虑:

数据特性: 采样率、信噪比、任务设计
科学问题: 关注离散状态切换 vs 连续演化
计算成本: HMM < DyNeMo < M-DyNeMo < TvDN
可解释性: 离散模型更易解释,连续模型更灵活

关于脑动态网络研究的一些方法和论文

相关文献汇总：

meg背景的文章

tvdn 时变动态网络模型

DyNeMo 动态功能脑网络

VAE的引入和两篇较新的文章

Hidden Semi-Markov Model（HSMM）

HSMM应用于脑网络的开创性论文

Shappell et al., 2019 - 脑网络HSMM的奠基之作

核心问题与创新

HMM的根本局限:

HSMM的解决方案:

方法学核心

1. 模型对比

2. HSMM数学框架

实验验证

仿真研究 (Simulation Study)

真实数据分析

数据1: 焦虑诱导任务态fMRI

数据2: HCP静息态fMRI

核心贡献

1. 方法学创新

2. 停留时间的神经科学意义

3. 与传统方法的比较

后续影响与应用

广泛采用 (2019-2025)

软件工具

方法学扩展

与其他动态方法的关系

发展脉络:

HSMM vs DyNeMo:

实践建议

1. 选择停留分布

2. 确定状态数

3. R实现

方法的讨论

发展历程概览

1. HMM (Hidden Markov Model) - 隐马尔可夫模型

2. DyNeMo (Dynamic Network Modes, 2022)

3. M-DyNeMo (Multiscale DyNeMo)

4. TvDN (Time-varying Dynamic Networks)

思想演进的核心脉络

认知转变:

数学表达:

实际应用考量

关键问题