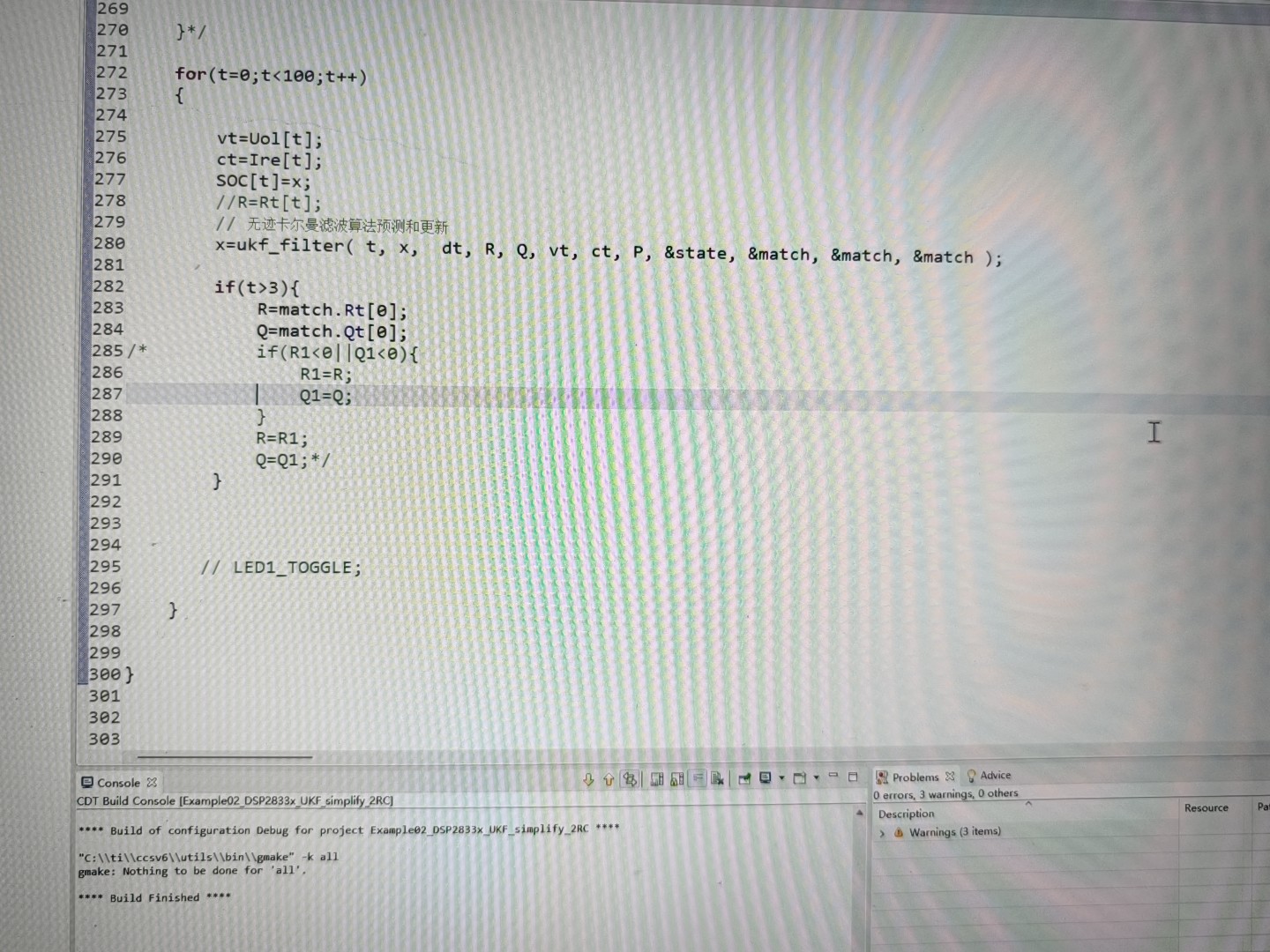
AUKF/自适应无迹卡尔曼滤波算法C代码,CCS6软件编译,微控为DSP28335,可下载运行。
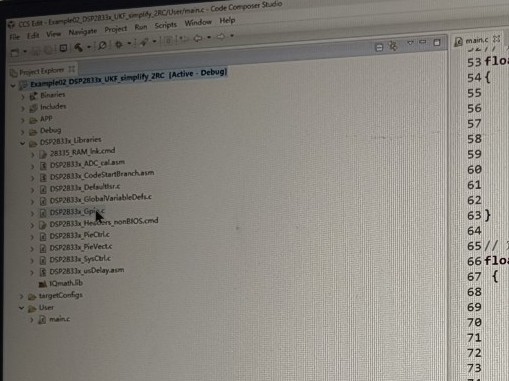
最近在研究滤波算法,其中自适应无迹卡尔曼滤波(AUKF)算法特别吸引我,于是决定在DSP28335微控上用C代码实现它,并使用CCS6软件进行编译,跟大家分享下这个过程。
AUKF算法简介
自适应无迹卡尔曼滤波算法是对传统无迹卡尔曼滤波的一种改进,它能够根据系统的实际情况自适应地调整滤波参数,从而在面对复杂多变的系统时,相比传统方法能更精准地估计状态。
C代码实现
下面是一段简化的AUKF算法C代码示例(仅核心部分):
c
#include "math.h"
// 定义状态向量和观测向量维度
#define STATE_DIM 2
#define OBS_DIM 1
// 定义结构体存储滤波状态
typedef struct {
float x_hat[STATE_DIM]; // 估计状态
float P[STATE_DIM][STATE_DIM]; // 估计协方差
float Q[STATE_DIM][STATE_DIM]; // 过程噪声协方差
float R[OBS_DIM][OBS_DIM]; // 观测噪声协方差
} AUKF_State;
// 初始化AUKF状态
void AUKF_Init(AUKF_State *aukf) {
for (int i = 0; i < STATE_DIM; i++) {
aukf->x_hat[i] = 0.0;
for (int j = 0; j < STATE_DIM; j++) {
aukf->P[i][j] = (i == j)? 1.0 : 0.0;
aukf->Q[i][j] = (i == j)? 0.01 : 0.0;
}
}
for (int i = 0; i < OBS_DIM; i++) {
for (int j = 0; j < OBS_DIM; j++) {
aukf->R[i][j] = (i == j)? 1.0 : 0.0;
}
}
}
// 状态转移函数
void f(float *x, float *x_out) {
x_out[0] = x[0] + 0.1 * x[1];
x_out[1] = x[1];
}
// 观测函数
void h(float *x, float *z_out) {
z_out[0] = x[0];
}
// AUKF预测步骤
void AUKF_Predict(AUKF_State *aukf) {
float x_pred[STATE_DIM];
f(aukf->x_hat, x_pred);
float P_pred[STATE_DIM][STATE_DIM];
for (int i = 0; i < STATE_DIM; i++) {
for (int j = 0; j < STATE_DIM; j++) {
P_pred[i][j] = 0.0;
for (int k = 0; k < STATE_DIM; k++) {
P_pred[i][j] += aukf->P[i][k] * aukf->P[j][k];
}
P_pred[i][j] += aukf->Q[i][j];
}
}
// 更新状态和协方差
for (int i = 0; i < STATE_DIM; i++) {
aukf->x_hat[i] = x_pred[i];
for (int j = 0; j < STATE_DIM; j++) {
aukf->P[i][j] = P_pred[i][j];
}
}
}
// AUKF更新步骤
void AUKF_Update(AUKF_State *aukf, float *z) {
float z_pred[OBS_DIM];
h(aukf->x_hat, z_pred);
float S[OBS_DIM][OBS_DIM];
for (int i = 0; i < OBS_DIM; i++) {
for (int j = 0; j < OBS_DIM; j++) {
S[i][j] = 0.0;
for (int k = 0; k < STATE_DIM; k++) {
for (int l = 0; l < STATE_DIM; l++) {
// 这里简单模拟计算,实际可能更复杂
S[i][j] += aukf->P[k][l];
}
}
S[i][j] += aukf->R[i][j];
}
}
float K[STATE_DIM][OBS_DIM];
// 计算卡尔曼增益
for (int i = 0; i < STATE_DIM; i++) {
for (int j = 0; j < OBS_DIM; j++) {
K[i][j] = 0.0;
for (int k = 0; k < STATE_DIM; k++) {
// 简单模拟计算
K[i][j] += aukf->P[i][k];
}
for (int l = 0; l < OBS_DIM; l++) {
// 这里需要对S求逆,实际代码更复杂
K[i][j] /= S[j][l];
}
}
}
// 更新状态和协方差
for (int i = 0; i < STATE_DIM; i++) {
for (int j = 0; j < OBS_DIM; j++) {
aukf->x_hat[i] += K[i][j] * (z[j] - z_pred[j]);
}
}
float temp_P[STATE_DIM][STATE_DIM];
for (int i = 0; i < STATE_DIM; i++) {
for (int j = 0; j < STATE_DIM; j++) {
temp_P[i][j] = 0.0;
for (int k = 0; k < OBS_DIM; k++) {
for (int l = 0; l < STATE_DIM; l++) {
// 简单模拟计算
temp_P[i][j] += K[i][k] * aukf->P[k][l];
}
}
aukf->P[i][j] -= temp_P[i][j];
}
}
}代码分析
- 结构体定义 :
AUKF_State结构体用于存储AUKF算法所需的各种状态,包括估计状态、估计协方差、过程噪声协方差和观测噪声协方差。这样的设计方便在程序中统一管理滤波的参数。 - 初始化函数
AUKFInit :在这个函数中,对状态向量xhat初始化为0,估计协方差矩阵P初始化为单位矩阵,过程噪声协方差矩阵Q和观测噪声协方差矩阵R也进行了初始化。这是算法运行前必要的准备工作,为后续的滤波过程提供初始条件。 - 状态转移函数
f和观测函数h:f函数定义了状态如何从当前时刻转移到下一时刻,在这个简单例子中,状态x[0]会随着x[1]的变化而变化,x[1]保持不变。h函数定义了如何从状态向量得到观测向量,这里简单地将x[0]作为观测值。 - 预测步骤
AUKFPredict :首先通过状态转移函数f得到预测状态xpred,然后计算预测协方差P_pred,考虑了当前估计协方差和过程噪声协方差。最后更新滤波的状态和协方差,为更新步骤做准备。 - 更新步骤
AUKFUpdate :通过观测函数h得到预测观测值zpred,计算观测预测协方差S。接着计算卡尔曼增益K,这里虽然代码是简化模拟计算,但实际中需要对矩阵进行复杂运算,比如求逆。最后根据卡尔曼增益更新状态和协方差,使滤波结果更接近真实值。
CCS6编译与DSP28335下载运行
- CCS6项目创建:打开CCS6软件,创建一个新的DSP28335项目。在项目设置中,配置好芯片型号、编译器选项等参数。确保编译器支持C语言标准,并且针对DSP28335进行了优化。
- 代码导入与编译:将上述AUKF算法的C代码添加到项目中。在编译之前,可能需要根据DSP28335的硬件资源对代码进行一些调整,比如内存分配等。点击编译按钮,CCS6会对代码进行语法检查和编译优化。如果有错误,根据错误提示修改代码,直到编译成功生成可执行文件。
- 下载运行:使用合适的仿真器(如XDS100v3等)连接DSP28335开发板和电脑。在CCS6中,选择下载并运行选项,将生成的可执行文件下载到DSP28335芯片中运行。可以通过设置断点、观察变量等方式调试程序,查看AUKF算法的运行效果,比如估计状态是否收敛到真实值,协方差是否合理变化等。
通过以上步骤,就成功地在DSP28335微控上实现了AUKF算法,并通过CCS6进行了编译和下载运行。希望这篇博文对正在研究相关内容的小伙伴有所帮助,欢迎一起交流探讨。