【基础篇007】GeoGebra工具系列_多边形(Polygon)

@心有矩，行有方；不逾界，自成章。------八荒启

@TOC

一. 🚀 引言

1. 背景

在传统教学中，画多边形只是个绘图动作。但在 GeoGebra 中，使用 "多边形"工具（或"向量多边形"工具）的瞬间，你创造的是一个活的数学对象。比如，如果你用的是两点定义多边形，那么这两个点就决定了多边形的长、宽、面积、周长；多边形绘制好后会立即在"代数区"同步生成其方程、所有顶点坐标、几何属性，方便关联其他元素；你可以随时拖动任何一个顶点或边，整个多边形及其所有关联数据（面积、对角线长度...）都会实时、连续地变化。那么本章，我们将从交互的角度一起研究一下多边形工具。

文章路径	公众号：八荒启-交互动画 / 创作中心 / 系列教程 / Geogebra从入门到编程全集 / 基础篇
作者	酷酷的脸脸
官方网址	八荒启-交互动画
更新日期	2025.12.13
资源下载	文章配套文件包，公众号内回复"GGB007B"（注意不要换行）

2. 场景

八荒启专精于制作交互动画，比如GGB、Canvas、H5、Unity，本套GGB系列文章主要是以交互动画为大背景，逐步展开具体知识点的讲解。（官网：八荒启-交互动画)

二、🛠️GeoGebra工具系列_多边形(Polygon)

1. 基石---重新认识"多边形"工具

核心问题：传统的画多边形与GeoGebra里的"画多边形"，本质区别是什么？

（1）多边形不只是图形

对于传统意义上的多边形绘制，主要突出的特点是：静态图形、纯视觉，比如在纸上画一个多边形，更多是一个描绘动作：

• 它的边看似平行，但不一定真的平行。
• 它的角看似直角，但精确度依赖画图工具。
• 画完之后，它就凝固在那里，无法改变。
• 学生看到的只是"像个多边形的图形"，而不是一个真正带数学性质的对象。

换句话来说：

传统课堂里，多边形是"图像"。你只能看，不能动，也无法从中提取更多数学信息。

但GeoGebra多边形：一个具有"数学生命"的动态对象

GeoGebra中绘制多边形非常简单，只需要激活多边形工具，然后在画布上点击点即可：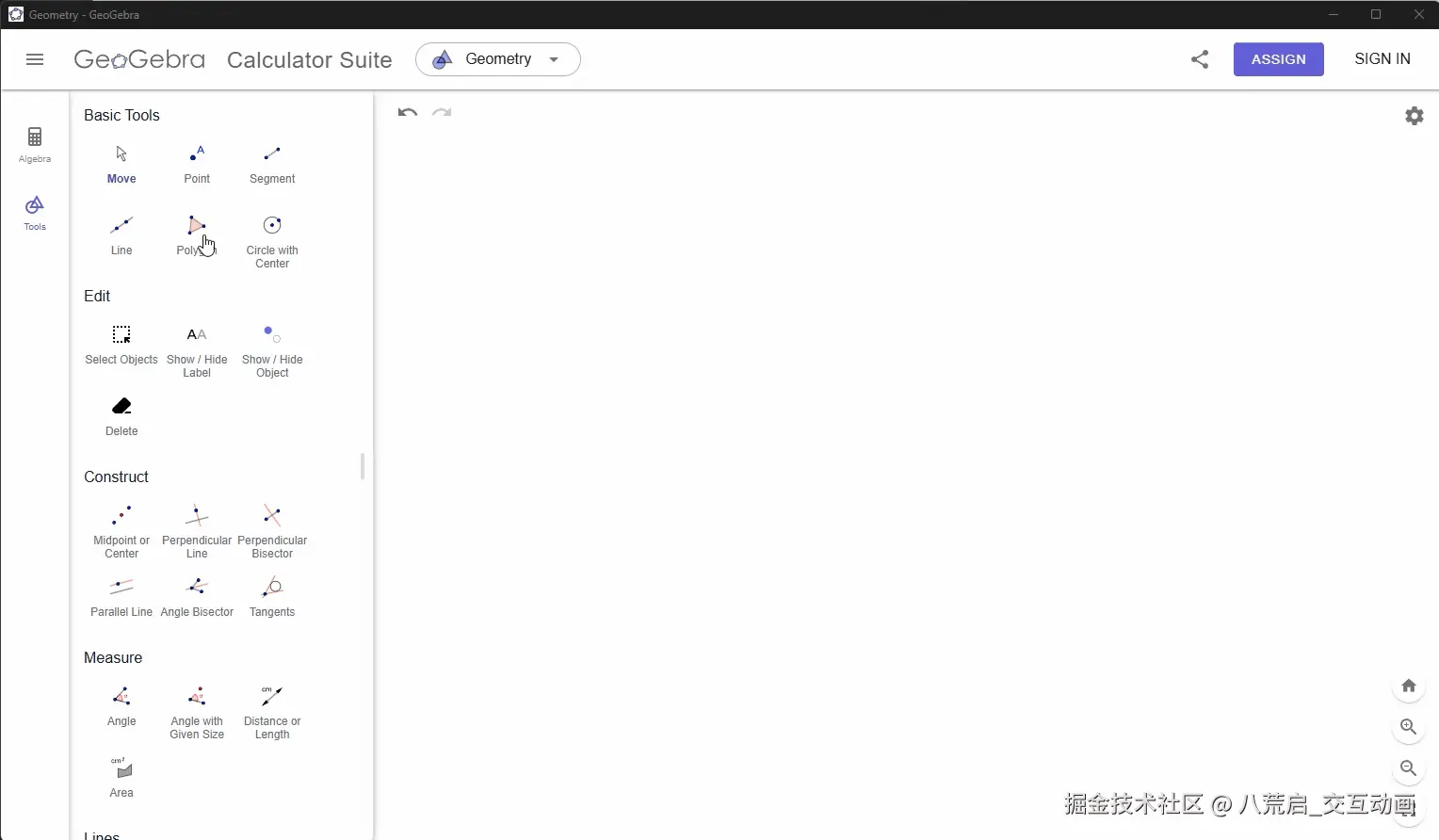

GGB的基础操作这里就不过多赘述了，摸索一下就好，都非常简单。

所以在这里，多边形就不只是一个图形了： 它自动具备：

• 顶点坐标（可实时更新）
• 边长（随拖动自动计算）
• 角度（保持直角关系）
• 平行、垂直等约束（软件自动维持）
• 面积、周长等属性（动态显示）
• 拖动后仍保持多边形本质（软件保证性质不被破坏）

在 GeoGebra 里，多边形是"数学对象"。你可以拖、可以测、可以变，它始终保持多边形的数学定义。

这里我汇总一下：

维度	传统画法（纸笔）	GeoGebra多边形
本质	静态图形	动态数学对象
精确度	依赖手、尺子、绘图技巧	自动保证精确（平行、垂直、直角）
可操作性	画完即固定，无法改变	可拖动、可变形但保持多边形性质
信息可见性	只能看到轮廓	坐标、边长、角度、面积等实时显示
数学关系	需要人为推理或标注	系统自动维护内部数学关系
探索性	很弱，无法实验	很强，可用于观察、猜想、验证定理
教学价值	展示为主	探究为主，可视化数学思想

（2）动态特性展示

如果我们有一个多边形，然后已经显示出了它的周长、面积、内角和，当我们拖动某个点或者某个边的时候当前多边形的性质是这样的： 注意：

Parameter(q1)  // 获取多边形的周长
Area(q1)  // 获取多边形的面积

看到这里是不是已经可以重新认识了多边形，对的，我们可以让学生逐步理解：几何图形是可以"呼吸"的数学对象，而不是死板的图。

如果说前面讲的点、线等都是一些基础操作，那么从这里开始，互动性就真正开始跃然纸上，比如当前的这个动画，学生通过拖动能看到：

• 改动一个点，为什么好像整个形状都被"牵动"？
• 面积为何突然变大？
• 哪些角的变化与哪些边有关？
• 周长和面积的变化有没有同步关系？

这种体验，比静止的图形更能帮助学生理解：

图形是由一系列约束与关系共同构成的系统，不只是几条线围起来的"形状"。（配套资源见文章头部表格）

（3）数学对象思维

在 GeoGebra 中，用工具创建的多边形（比如刚才提到的多边形）不只是由几条线围成的图，而是一个具有结构、约束和属性的数学对象。这种"对象思维"是传统纸笔几何较难培养的，但在动态几何环境里可以自然生长。 比如在传统几何课中，学生画一个四边形，往往关注的是：边画直了吗？看起来像不像？有没有闭合？这是典型的"图像思维"。

但在 GeoGebra 中，多边形是由一系列点与点之间的关系定义的，顶点是可以移动的对象，边是由顶点实时决定的线段 ，内角与面积是可计算的量，形状随拖动而变动，但结构关系保持，学生逐渐不再"画图"，而是在操控一个由数学约束构成的系统。

为了方便观察，我这里把动态几何下的"观察 → 猜想 → 验证"科学思维与实验性数学整理成一个表格：

阶段	学生活动	示例问题	目标与体验
观察（Observe）	拖动四边形顶点，测量边长、角度、面积	"四边形的内角和是不是总是 360°？"	直接得到现象，理解图形属性随操作变化
猜想（Hypothesize）	对观察结果提出规律或假设	"如果我把一个角拉成凹角，面积为什么变小？" "对边的关系会不会一直保持？"	培养预测能力与逻辑思维，形成数学假设
验证（Verify）	通过动态拖动、测量、观察来检验猜想	"是不是所有四边形都能分成两个三角形？"	通过实验验证规律，理解数学对象的稳定性与约束关系

重新认识了一下"多边形"工具，你是否有什么收获呢？这里我没有大篇幅讲解如何操作，但是从交互的角度讲解了一下GeoGebra中"多边形"工具的独特含义。最后，我汇总一下数学作为可实验的对象的表现与意义

特性	表现与意义
可试探	学生可以自由改变图形顶点位置，探索不同形状的性质
可调整	图形属性随操作变化，帮助学生发现规律的条件
可实验	通过动态拖动和测量，进行"数学实验"，验证或反驳假设
可验证	数学性质可以被重复测试和观察，不依赖记忆
可反驳	错误假设可以通过操作立即发现，培养批判性思维

数学不是死知识，而是一套可操控、可验证、可推理的结构系统。多边形是培养"数学对象思维"的最佳入口。
------八荒启

2. 解密---工具背后的代数世界

核心问题：当我拖动多边形时，代数区里发生了什么？

在 GeoGebra 中，拖动并不是"随便动一动图形"，而是一次几何操作驱动代数系统实时重算的过程。理解这一点，是从"会用工具"走向"理解工具"的关键一步。

（1）坐标与约束关系

当你用"多边形工具"创建一个多边形时，GeoGebra 首先做的不是画边，而是定义点。比如我们重新打开一个GGB界面，然后用多边形工具创建一个多边形：

左边代数区可以发现不是只有一句指令，而是有七行：

A=(-6.0965,6.74676)
B=(-10.84531,2.42577)
C=(-3.35845,1.69848)
t1=Polygon(A,B,C)
a=Segment(B,C,t1)
b=Segment(C,A,t1)
c=Segment(A,B,t1)

仔细观察发现，前三行是点的定义，接着是多边形的定义，最后是三个线段的定义，这个就很好理解了：

当你用"多边形工具"创建一个多边形时，GeoGebra 首先做的不是画边，而是定义点。每一个顶点本质上都是一个有序数对：

<math xmlns="http://www.w3.org/1998/Math/MathML"> A ( x 1 , y 1 ) , B ( x 2 , y 2 ) , C ( x 3 , y 3 ) , ... A(x1,y1),B(x2,y2),C(x3,y3),... </math>A(x1,y1),B(x2,y2),C(x3,y3),...

如果我们拖动其中一个顶点，会发现：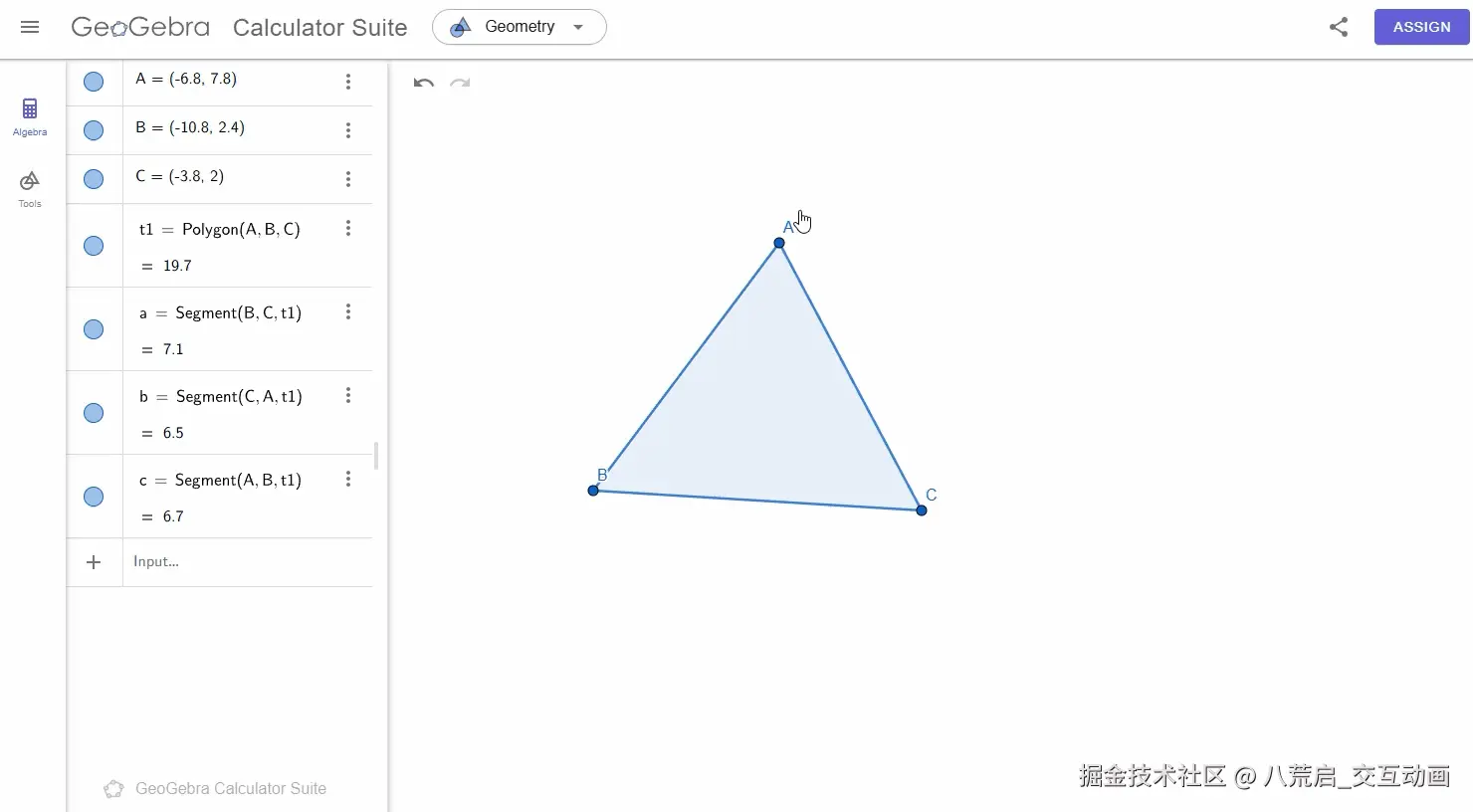

对应点的坐标在不停的改变，多边形的面积数值在变化（Polygon指令默认返回的是多边形的面积），多边形对应的边也在发生变化。

汇总一下，当你拖动某一个顶点时：

• 该点的坐标立即发生变化
• 与它相连的边随之重算
• 整个多边形的结构被重新计算

虽然学生看到的只是"图形在动"，而代数区中发生的是：一组变量正在被实时更新，这正是GGB创作的灵魂思路。比如我们可以将这些变化的量作为参数去创建其他图形，就可以实现联动效果，这也正是代数约束在后台持续起作用的结果。

（2）即时反馈机制

GeoGebra 的强大之处在于：代数不是事后计算，而是实时反馈。

当我们拖动多边形的一个顶点时：

• 每条边的长度自动更新（多边形形成的时候软件就会自动创建好）
• 各个内角大小重新计算（需要使用Angle指令提取）
• 周长与面积立即刷新（面积已经有了，周长需要用Perimeter指令提取）
• 对角线同步变化（需要构造，然后提取长度等信息）

慢慢的你会发现，GGB真正强大的功能不是工具栏，恰恰相反，工具栏只占GGB全部功能的2%，而代数区占了全部功能的28%（剩下的70%是GGB的指令脚本系统）

经过前面几篇的学习和了解，恭喜你逐渐入门GGB，那么这里我总结一下GGB创作的核心思路：

代数区是动画"看不见的引擎"，代数区中不断变化的数值，实际上是多边形内部属性的可视化呈现。
主要体现为：
1. 数值的变化 ↔ 图形形状的变化
2. 数值的稳定 ↔ 图形性质的不变

这也是几何画板根本无法和GGB比较的原因，从软件的设计初衷来看，GGB领先于几何画板好几个时代。

当然，学生也可以意识到一点：几何图形的每一次变化，都有代数层面的对应。

（3）从操作到理解

拖动如果只是"好玩"，意义有限，但当拖动与思考结合，就变成了理解的通道。 多边形工具的使用，已经可以实现很多教育效果，比如通过拖动观察"哪些变，哪些不变"，教师可以引导学生反复拖动多边形，并引导思考：

• 顶点坐标变了吗？（变）
• 边长和角度变了吗？（通常变）
• 多边形的边数变了吗？（不变）
• 内角和是否保持不变？（多边形内角和的计算）

这种对比帮助学生区分，变量 vs 不变量，是数学思维中极其重要的一步。（当然，创作GGB的话数学思维必不可少）

当然这里只是一个简单的例子，如果我们对这个松树进行一定的关系约束，比如这种：

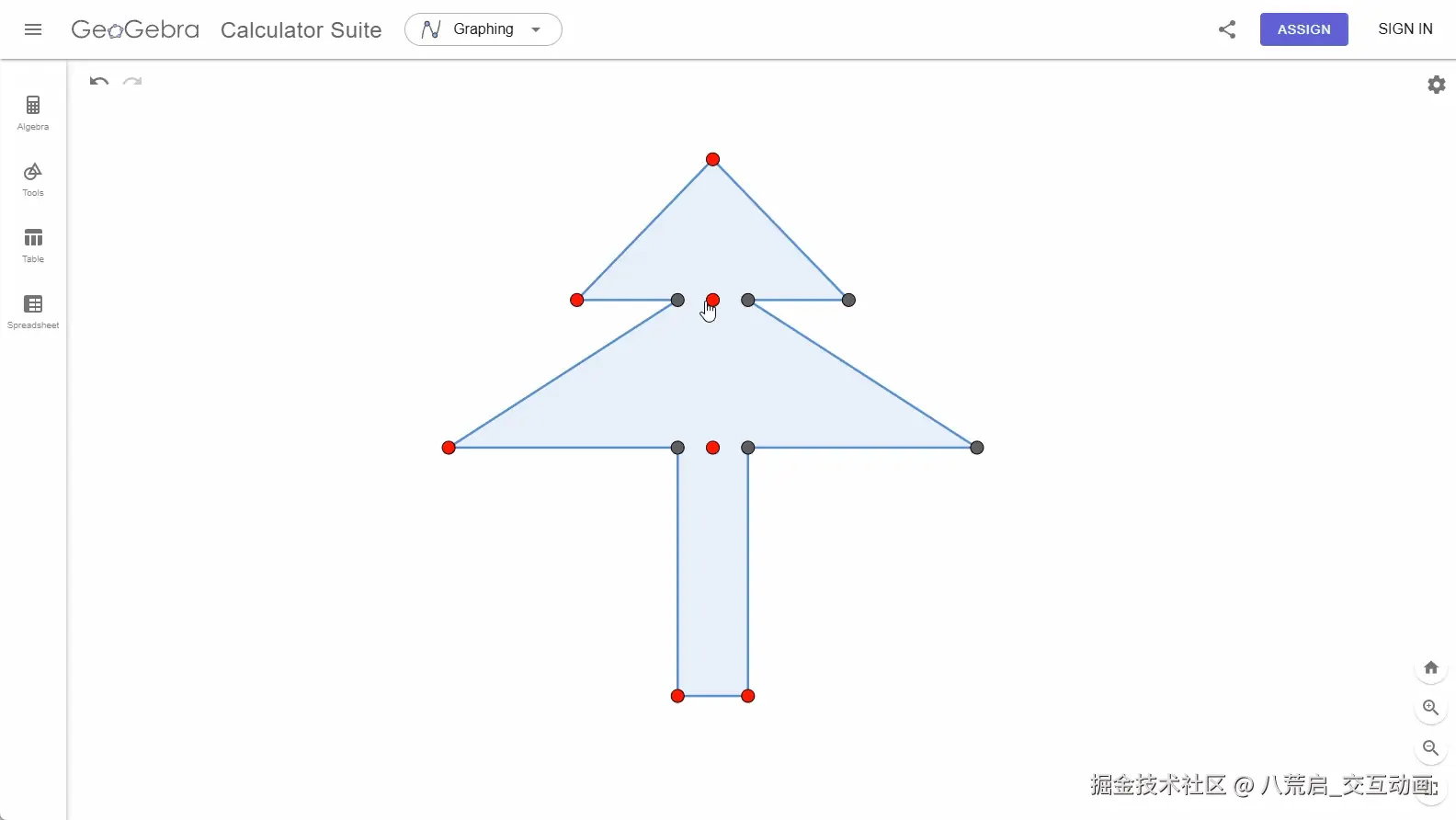那就可以从几何中的"拖动"，逐渐理解到代数中的"变量变化"，再到几何中的"性质保持"，以及代数中的"关系约束"。（当前演示作品配套文件见文章首部表格，制作不复杂，可以参考）

当你能想到图形之所以没变形，是因为某些代数关系一直成立，说明就已经开始用数学对象的语言在思考问题了。

3. 融合---跨领域的连接与应用

核心问题：多边形工具能用在数学之外的场景吗？

在现实世界中，我们几乎看不到"完美的圆"，却到处都是由直线围成的区域。从设计图纸到工程结构，从城市街区到生活空间，多边形是描述现实世界最自然、最常用的数学语言之一。GeoGebra 的多边形工具，正好为这种"现实---数学"的连接提供了桥梁。

比如这个踏板，就是多边形工具最经典的使用： 这里我汇总一下多边形工具在整个交互动画领域的常见使用方式：

专题名称	多边形在交互动画中的核心作用	典型制作场景
画面构图	作为背景块面与画面结构单元	场景搭建、画面比例调整
区域划分	划定功能区与交互区	操作区 / 显示区分离
遮罩与限制	限制显示或操作范围	区域内有效交互
角色轮廓	作为物体或角色的简化外形	轻量级动画角色
结构骨架	作为动画的几何骨架	框架、机构演示
变形结构	拖动顶点引发整体变形	拉伸、压缩动画
运动边界	限制对象的运动范围	防止越界
路径依附	为运动对象提供参考边	沿边移动、贴边动画
参数承载	面积、周长作为动态参数	数值驱动动画变化
间接控制	通过形状变化控制动画状态	减少滑块依赖
状态反馈	颜色、透明度变化提示状态	即时反馈
条件触发	作为几何判断条件	简单交互逻辑
场景建模	构建完整交互场景轮廓	情境化动画
教学演示	可被拖动的演示对象	探索式学习
实验操作	支持反复操作与验证	"试一试"型动画
对象组织	作为多个对象的参考基准	动画结构管理
依赖关系	构建对象间的依赖网络	保持系统稳定
动画系统	作为底层建模单元	完整交互动画

本篇讲解的内容稍微倾向于底层逻辑的梳理与交互动画创作思路的培养，当然，也是因为多边形工具非常重要，且是众多动画根基的缘故。动画工具本身非常简单，但是背后涉及到的理论和思路，值得我们深究。

三. ✨结尾

本文配套文件已上传，资料获取方式见文章首部表格。

---

本文收录于微信公众号：八荒启-交互动画，可点击扫码关注，更多技术咨询与服务，可直接访问官方网站获取：bahuangqi.com/（电脑打开）