From Nand to Tetris 里的 Project 2

背景

让我们按照 From Nand to Tetris 里 Project 2 的要求，来完成下列的设计。

实现半加器(HalfAdder)
实现全加器(FullAdder)
实现 <math xmlns="http://www.w3.org/1998/Math/MathML"> 16 16 </math>16 位加法器(Add16)
实现 <math xmlns="http://www.w3.org/1998/Math/MathML"> 16 16 </math>16 位自增器(Inc16)
实现算术逻辑单元(ALU) (todo)

正文

1. 实现 `HalfAdder`

前往 Nand to Tetris Online IDE，选择 Project 2 里的 HalfAdder，效果如下图所示 ⬇️

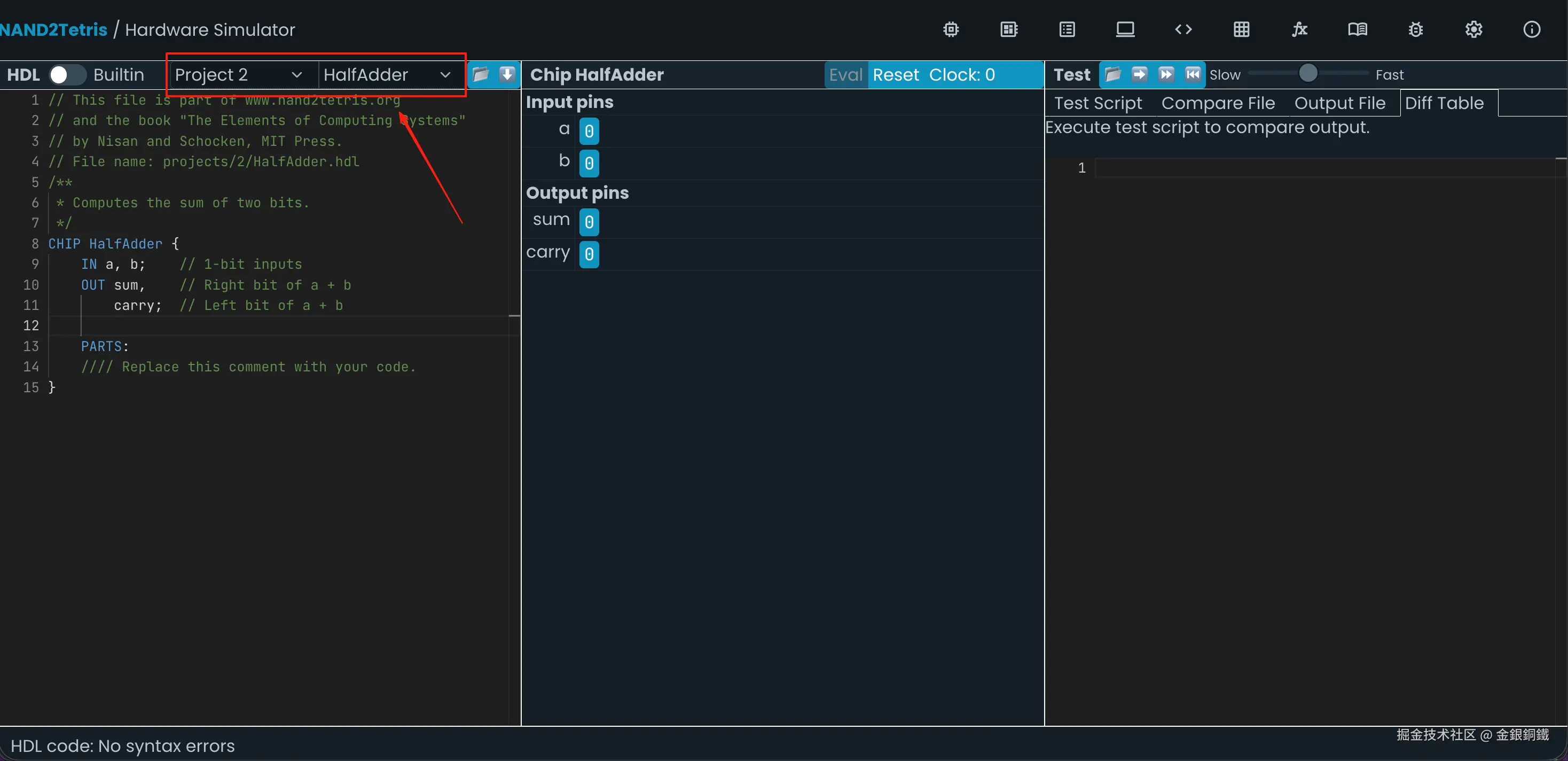
我们的目标是用 Project 1 里已经实现的各种 chip 实现一个 HalfAdder。

输入是
- <math xmlns="http://www.w3.org/1998/Math/MathML"> a a </math>a
- <math xmlns="http://www.w3.org/1998/Math/MathML"> b b </math>b
输出是
- <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m sum </math>sum
- <math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y carry </math>carry

我们可以从它的真值表入手 ⬇️

<math xmlns="http://www.w3.org/1998/Math/MathML"> a a </math>a	<math xmlns="http://www.w3.org/1998/Math/MathML"> b b </math>b	<math xmlns="http://www.w3.org/1998/Math/MathML"> s u m sum </math>sum	<math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y carry </math>carry
<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0
<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0
<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0
<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1

可见

<math xmlns="http://www.w3.org/1998/Math/MathML"> s u m = ( ¬ a ∧ b ) ∨ ( a ∧ ¬ b ) = a ⊕ b sum=(\neg{a}\land b) \lor (a\land \neg{b})=a\oplus b </math>sum=(¬a∧b)∨(a∧¬b)=a⊕b
<math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y = a ∧ b carry=a\land b </math>carry=a∧b

所以可以这样实现 ⬇️

hdl 复制代码

CHIP HalfAdder {
    IN a, b;    // 1-bit inputs
    OUT sum,    // Right bit of a + b 
        carry;  // Left bit of a + b

    PARTS:
    And(a= a, b= b, out= carry);
    Xor(a = a, b = b, out = sum);
}

这样的代码可以通过仿真测试，效果如下图所示 ⬇️

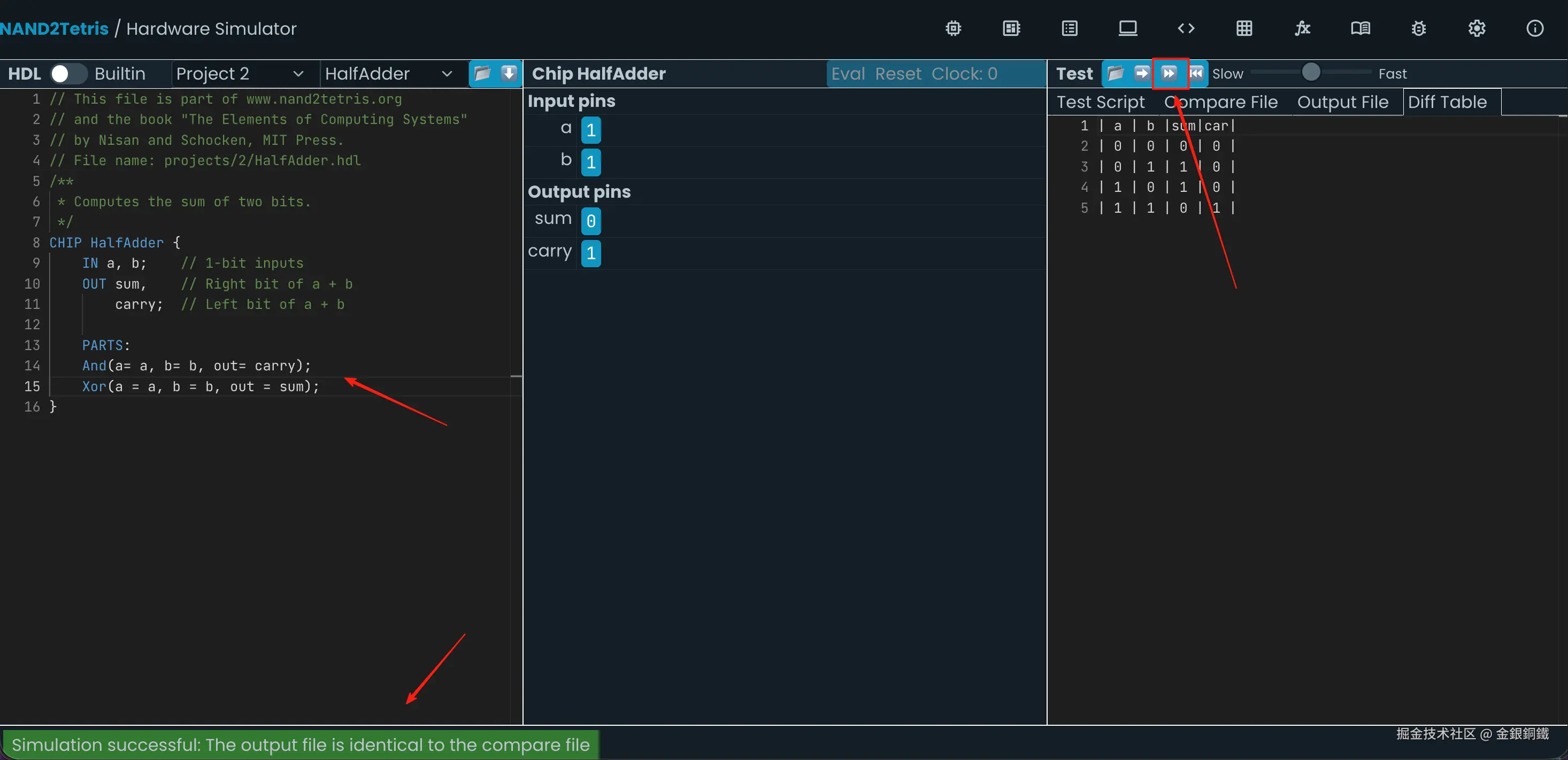
2. 实现 `FullAdder`

前往 Nand to Tetris Online IDE，选择 Project 2 里的 FullAdder，效果如下图所示 ⬇️

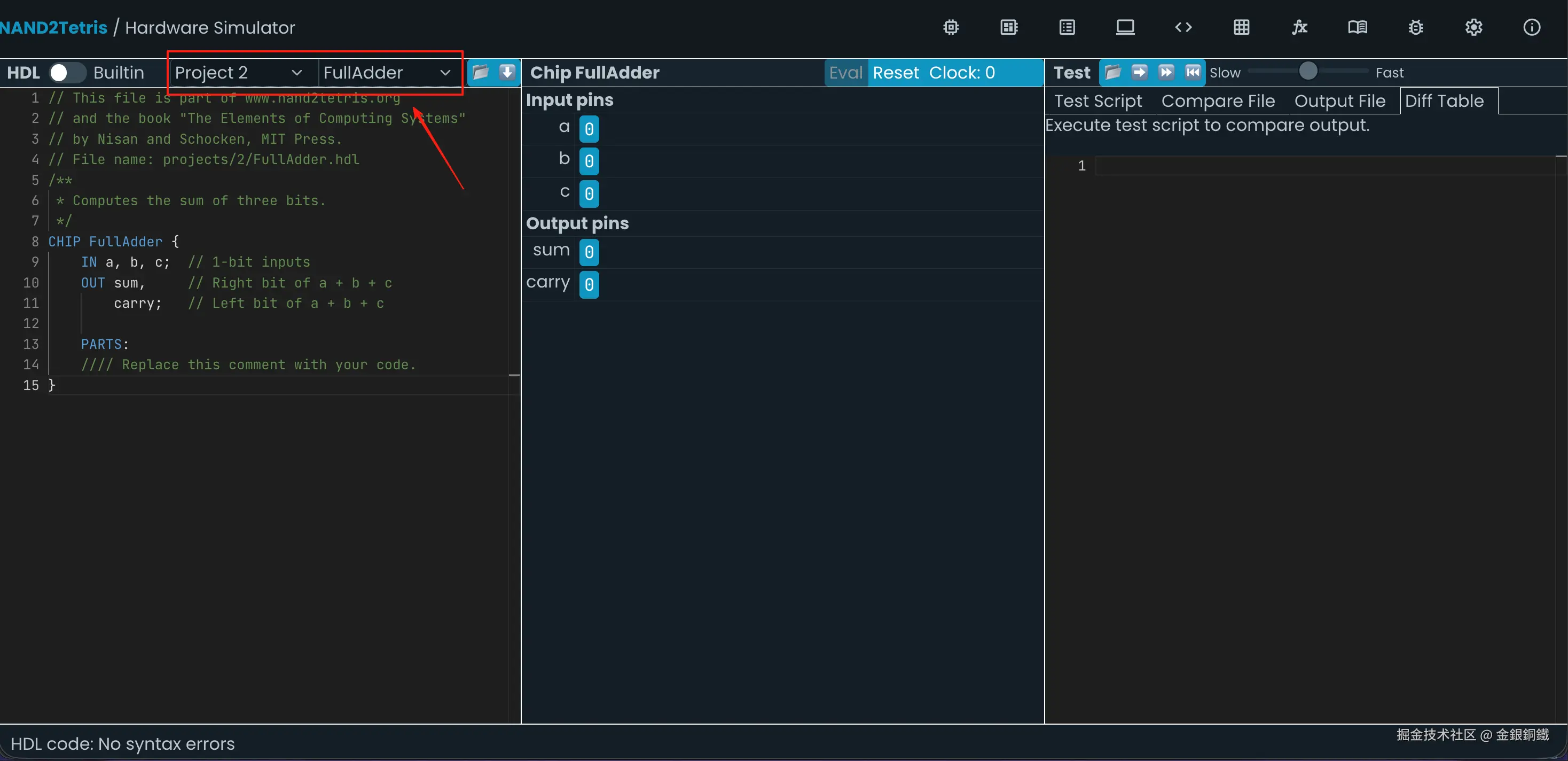
我们的目标是用 Project 1 里已经实现的各种 chip，以及刚才实现的 HalfAdder 来实现一个 FullAdder。

输入是
- <math xmlns="http://www.w3.org/1998/Math/MathML"> a a </math>a
- <math xmlns="http://www.w3.org/1998/Math/MathML"> b b </math>b
- <math xmlns="http://www.w3.org/1998/Math/MathML"> c c </math>c
输出是
- <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m sum </math>sum
- <math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y carry </math>carry

我们还是从真值表入手 ⬇️

<math xmlns="http://www.w3.org/1998/Math/MathML"> a a </math>a	<math xmlns="http://www.w3.org/1998/Math/MathML"> b b </math>b	<math xmlns="http://www.w3.org/1998/Math/MathML"> c c </math>c	<math xmlns="http://www.w3.org/1998/Math/MathML"> s u m sum </math>sum	<math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y carry </math>carry
<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0
<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0
<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0
<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1
<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0
<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1
<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1
<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1	<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1

通过观察真值表，可以将 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m sum </math>sum 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y carry </math>carry 写成对应的析取范式 DNF(Disjunctive Normal Form) 的形式

<math xmlns="http://www.w3.org/1998/Math/MathML"> s u m = ( ¬ a ∧ ¬ b ∧ c ) ∨ ( ¬ a ∧ b ∧ ¬ c ) ∨ ( a ∧ ¬ b ∧ ¬ c ) ∨ ( a ∧ b ∧ c ) sum=(\neg{a}\land \neg{b}\land c)\lor (\neg{a}\land b\land \neg{c})\lor(a\land\neg{b}\land \neg{c})\lor(a\land b\land c) </math>sum=(¬a∧¬b∧c)∨(¬a∧b∧¬c)∨(a∧¬b∧¬c)∨(a∧b∧c)
<math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y = ( ¬ a ∧ b ∧ c ) ∨ ( a ∧ ¬ b ∧ c ) ∨ ( a ∧ b ∧ ¬ c ) ∨ ( a ∧ b ∧ c ) carry=(\neg{a}\land b\land c)\lor(a\land \neg{b}\land c)\lor(a\land b\land \neg{c})\lor(a\land b\land c) </math>carry=(¬a∧b∧c)∨(a∧¬b∧c)∨(a∧b∧¬c)∨(a∧b∧c)

从上面的析取范式出发，我们可以只用 And/Or/Not 来实现 FullAdder。但有没有更简洁的实现方式呢？我们回忆一下 HalfAdder 中的 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m sum </math>sum 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y carry </math>carry 是怎样的 ⬇️ （为了和 FullAdder 的 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m sum </math>sum 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y carry </math>carry 进行区分，我把 HalfAdder <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m sum </math>sum 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y carry </math>carry 分别改写为的 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m h a sum_{ha} </math>sumha 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y h a carry_{ha} </math>carryha）

<math xmlns="http://www.w3.org/1998/Math/MathML"> s u m h a = ( ¬ a ∧ b ) ∨ ( a ∧ ¬ b ) = a ⊕ b sum_{ha}=(\neg{a}\land b) \lor (a\land \neg{b})=a\oplus b </math>sumha=(¬a∧b)∨(a∧¬b)=a⊕b
<math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y h a = a ∧ b carry_{ha}=a\land b </math>carryha=a∧b

为了便于区分，我把 FullAdder 的 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m sum </math>sum 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y carry </math>carry 分别改写为 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m f a sum_{fa} </math>sumfa 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y f a carry_{fa} </math>carryfa。先看 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m f a sum_{fa} </math>sumfa 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m h a sum_{ha} </math>sumha 是否有关联。

<math xmlns="http://www.w3.org/1998/Math/MathML"> s u m f a = ( ¬ a ∧ ¬ b ∧ c ) ∨ ( ¬ a ∧ b ∧ ¬ c ) ∨ ( a ∧ ¬ b ∧ ¬ c ) ∨ ( a ∧ b ∧ c ) sum_{fa}=(\neg{a}\land \neg{b}\land c)\lor (\neg{a}\land b\land \neg{c})\lor(a\land\neg{b}\land \neg{c})\lor(a\land b\land c) </math>sumfa=(¬a∧¬b∧c)∨(¬a∧b∧¬c)∨(a∧¬b∧¬c)∨(a∧b∧c)
<math xmlns="http://www.w3.org/1998/Math/MathML"> s u m h a = a ⊕ b sum_{ha}=a\oplus b </math>sumha=a⊕b

如何表示 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m sum </math>sum

一个思路是看看能否将 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m f a sum_{fa} </math>sumfa 用 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m h a sum_{ha} </math>sumha 表示出来，我试了试，觉得有些繁琐，而且不容易想到。另一个思路是，我们从 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m f a sum_{fa} </math>sumfa 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m h a sum_{ha} </math>sumha 背后的含义入手。 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m h a sum_{ha} </math>sumha 表示 <math xmlns="http://www.w3.org/1998/Math/MathML"> a , b a,b </math>a,b 的和（忽略进位），所以 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m h a = a ⊕ b sum_{ha}=a\oplus b </math>sumha=a⊕b。

<math xmlns="http://www.w3.org/1998/Math/MathML"> s u m h a = 0 sum_{ha}=0 </math>sumha=0 时，只有 <math xmlns="http://www.w3.org/1998/Math/MathML"> c = 1 c=1 </math>c=1， <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m f a = 1 sum_{fa}=1 </math>sumfa=1 才会成立
<math xmlns="http://www.w3.org/1998/Math/MathML"> s u m h a = 1 sum_{ha}=1 </math>sumha=1 时，只有 <math xmlns="http://www.w3.org/1998/Math/MathML"> c = 0 c=0 </math>c=0， <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m f a = 1 sum_{fa}=1 </math>sumfa=1 才会成立

所以 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m f a = s u m h a ⊕ c sum_{fa}=sum_{ha}\oplus c </math>sumfa=sumha⊕c

而 HalfAdder 的作用就是对输入 <math xmlns="http://www.w3.org/1998/Math/MathML"> a , b a,b </math>a,b 分别执行 <math xmlns="http://www.w3.org/1998/Math/MathML"> ⊕ \oplus </math>⊕ 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∧ \land </math>∧ 运算，所以 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m f a sum_{fa} </math>sumfa 可以通过拼接两个 HalfAdder 来实现 ⬇️

第一个 HalfAdder 以 <math xmlns="http://www.w3.org/1998/Math/MathML"> a , b a,b </math>a,b 为输入，其 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m h a 1 = a ⊕ b sum_{ha1}=a\oplus b </math>sumha1=a⊕b
第二个 HalfAdder 以 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m f a 1 sum_{fa1} </math>sumfa1 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> c c </math>c 为输入，其 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m h a 2 = s u m f a 1 ⊕ c = sum_{ha2}=sum_{fa1}\oplus c= </math>sumha2=sumfa1⊕c=

如何表示 <math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y carry </math>carry

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> c a r r y f a = ( ¬ a ∧ b ∧ c ) ∨ ( a ∧ ¬ b ∧ c ) ∨ ( a ∧ b ∧ ¬ c ) ∨ ( a ∧ b ∧ c ) carry_{fa}=(\neg{a}\land b\land c)\lor(a\land \neg{b}\land c)\lor(a\land b\land \neg{c})\lor(a\land b\land c) </math>carryfa=(¬a∧b∧c)∨(a∧¬b∧c)∨(a∧b∧¬c)∨(a∧b∧c)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> = ( ¬ a ∧ b ∧ c ) ∨ ( a ∧ ¬ b ∧ c ) ∨ ( ( a ∧ b ∧ ¬ c ) ∨ ( a ∧ b ∧ c ) ) =(\neg{a}\land b\land c)\lor(a\land \neg{b}\land c)\lor((a\land b\land \neg{c})\lor(a\land b\land c)) </math>=(¬a∧b∧c)∨(a∧¬b∧c)∨((a∧b∧¬c)∨(a∧b∧c))
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> = ( ¬ a ∧ b ∧ c ) ∨ ( a ∧ ¬ b ∧ c ) ∨ ( a ∧ b ) =(\neg{a}\land b\land c)\lor(a\land \neg{b}\land c)\lor(a\land b) </math>=(¬a∧b∧c)∨(a∧¬b∧c)∨(a∧b)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> = ( ¬ a ∧ b ∧ c ) ∨ ( a ∧ ¬ b ∧ c ) ∨ c a r r y h a =(\neg{a}\land b\land c)\lor(a\land \neg{b}\land c)\lor carry_{ha} </math>=(¬a∧b∧c)∨(a∧¬b∧c)∨carryha
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> = ( ( a ⊕ b ) ∧ c ) ∨ c a r r y h a =((a\oplus b)\land c)\lor carry_{ha} </math>=((a⊕b)∧c)∨carryha
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> = ( s u m h a ∧ c ) ∨ c a r r y h a =(sum_{ha}\land c)\lor carry_{ha} </math>=(sumha∧c)∨carryha

考虑到 HalfAdder 的作用就是对输入 <math xmlns="http://www.w3.org/1998/Math/MathML"> a , b a,b </math>a,b 分别执行 <math xmlns="http://www.w3.org/1998/Math/MathML"> ⊕ \oplus </math>⊕ 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∧ \land </math>∧ 运算，所以 <math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y f a carry_{fa} </math>carryfa 可以通过拼接两个 HalfAdder 再加上一个 Or 运算 来实现 ⬇️

第一个 HalfAdder 以 <math xmlns="http://www.w3.org/1998/Math/MathML"> a , b a,b </math>a,b 为输入，它的
- <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m f a 1 = a ⊕ b sum_{fa1}=a\oplus b </math>sumfa1=a⊕b
- <math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y h a 1 = a ∧ b carry_{ha1}=a\land b </math>carryha1=a∧b
第二个 HalfAdder 以 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m f a 1 sum_{fa1} </math>sumfa1 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> c c </math>c 为输入，它的
- <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m h a 2 = s u m f a 1 ⊕ c sum_{ha2}=sum_{fa1}\oplus c </math>sumha2=sumfa1⊕c
- <math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y h a 2 = s u m f a 1 ∧ c carry_{ha2}=sum_{fa1}\land c </math>carryha2=sumfa1∧c

那么
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> c a r r y f a = ( s u m h a 1 ∧ c ) ∨ c a r r y h a 1 = c a r r y h a 2 ∨ c a r r y h a 1 carry_{fa}=(sum_{ha1}\land c)\lor carry_{ha1}=carry_{ha2}\lor carry_{ha1} </math>carryfa=(sumha1∧c)∨carryha1=carryha2∨carryha1

至此我们可以用 HalfAdder 和 Or 来实现 FullAdder。具体的代码如下 ⬇️

hdl 复制代码

CHIP FullAdder {
    IN a, b, c;  // 1-bit inputs
    OUT sum,     // Right bit of a + b + c
        carry;   // Left bit of a + b + c

    PARTS:
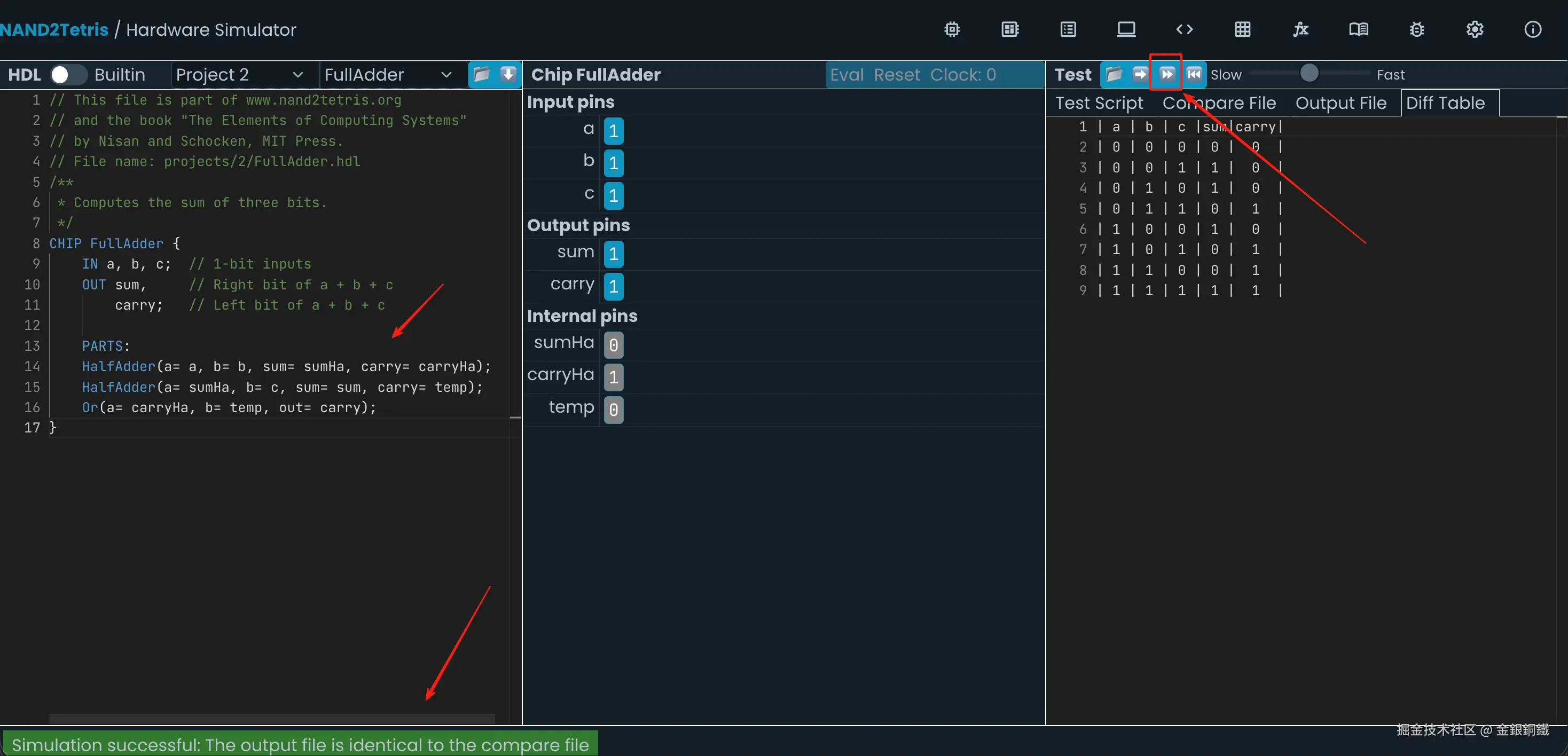
    HalfAdder(a= a, b= b, sum= sumHa, carry= carryHa);
    HalfAdder(a= sumHa, b= c, sum= sum, carry= temp);
    Or(a= carryHa, b= temp, out= carry);
}

这样的代码可以通过仿真测试，效果如下图所示 ⬇️

3. 实现 <math xmlns="http://www.w3.org/1998/Math/MathML"> 16 16 </math>16 位加法器(`Add16`)

前往 Nand to Tetris Online IDE，选择 Project 2 里的 Add16，效果如下图所示 ⬇️

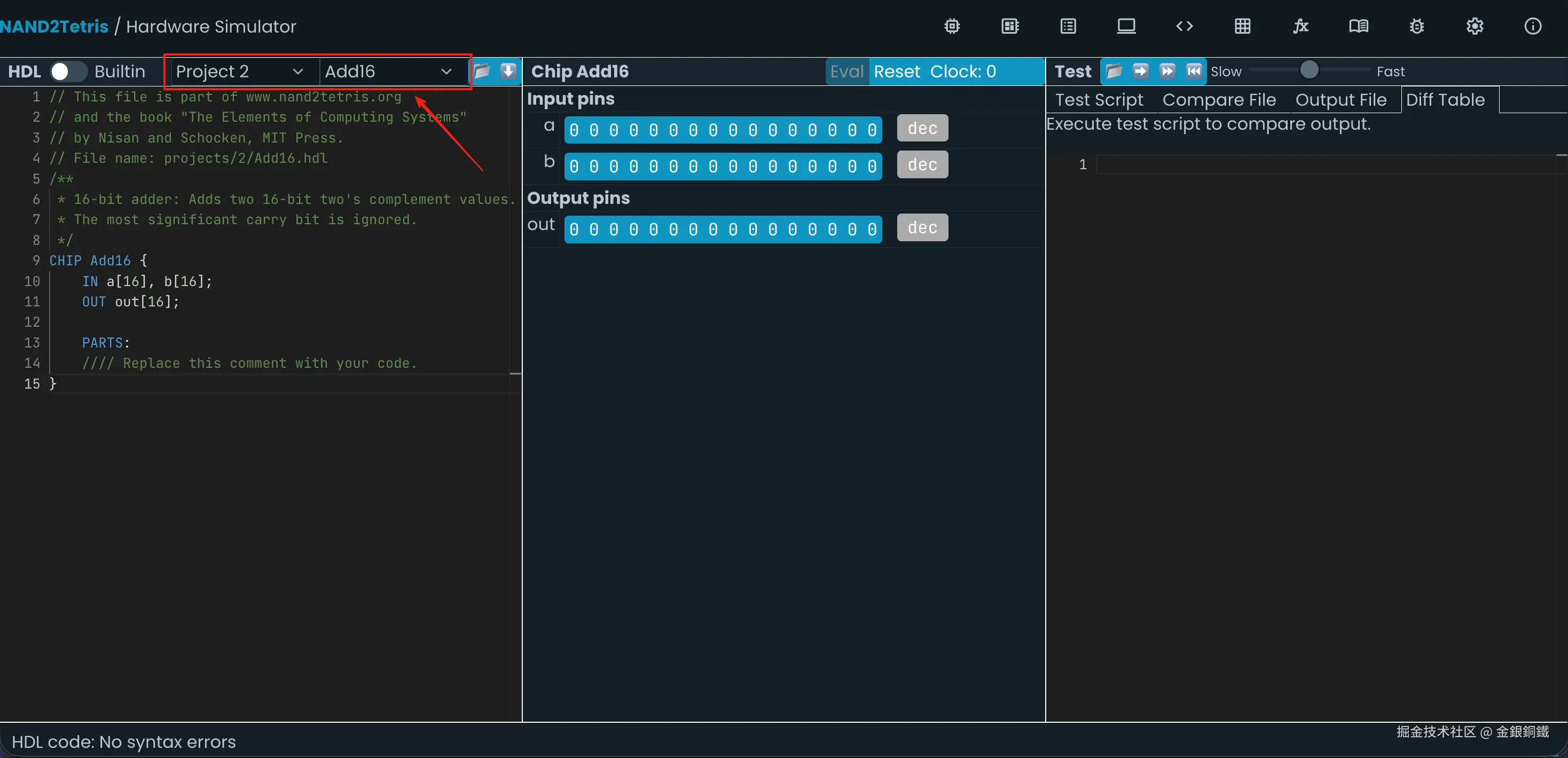
我们的目标是用 Project 1 里已经实现的各种 chip，以及刚才实现的 HalfAdder/FullAdder 来实现一个 Add16。

输入是
- <math xmlns="http://www.w3.org/1998/Math/MathML"> a [ 16 ] a[16] </math>a[16]
- <math xmlns="http://www.w3.org/1998/Math/MathML"> b [ 16 ] b[16] </math>b[16]
输出是
- <math xmlns="http://www.w3.org/1998/Math/MathML"> o u t [ 16 ] out[16] </math>out[16]

要实现的逻辑如下 ⬇️

text 复制代码

16-bit adder: Adds two 16-bit two's complement values.
The most significant carry bit is ignored.

我写了如下的 java 程序来生成对应的 HDL 代码

java 复制代码

import java.util.StringJoiner;

public class Adder16HdlCodeGenerator {
    public static void main(String[] args) {
        String template = """
                CHIP Add16 {
                    IN a[16], b[16];
                    OUT out[16];
                
                    PARTS:
                %s
                }
                """;
        StringJoiner joiner = new StringJoiner(System.lineSeparator());
        joiner.add("    FullAdder(a= a[0], b= b[0], c= false, sum= out[0], carry= c0);");
        for (int i = 1; i < 16; i++) {
            String line = String.format("    FullAdder(a= a[%s], b= b[%s], c= c%s, sum= out[%s], carry= c%s);", i, i, i - 1, i, i);
            joiner.add(line);
        }
        System.out.printf(template, joiner);
    }
}

请将以上 java 代码保存为 Adder16HdlCodeGenerator.java。用以下命令可以编译 Adder16HdlCodeGenerator.java 并运行其中的 main 方法。

bash 复制代码

javac Adder16HdlCodeGenerator.java
java Adder16HdlCodeGenerator

运行结果如下

hdl 复制代码

CHIP Add16 {
    IN a[16], b[16];
    OUT out[16];

    PARTS:
    FullAdder(a= a[0], b= b[0], c= false, sum= out[0], carry= c0);
    FullAdder(a= a[1], b= b[1], c= c0, sum= out[1], carry= c1);
    FullAdder(a= a[2], b= b[2], c= c1, sum= out[2], carry= c2);
    FullAdder(a= a[3], b= b[3], c= c2, sum= out[3], carry= c3);
    FullAdder(a= a[4], b= b[4], c= c3, sum= out[4], carry= c4);
    FullAdder(a= a[5], b= b[5], c= c4, sum= out[5], carry= c5);
    FullAdder(a= a[6], b= b[6], c= c5, sum= out[6], carry= c6);
    FullAdder(a= a[7], b= b[7], c= c6, sum= out[7], carry= c7);
    FullAdder(a= a[8], b= b[8], c= c7, sum= out[8], carry= c8);
    FullAdder(a= a[9], b= b[9], c= c8, sum= out[9], carry= c9);
    FullAdder(a= a[10], b= b[10], c= c9, sum= out[10], carry= c10);
    FullAdder(a= a[11], b= b[11], c= c10, sum= out[11], carry= c11);
    FullAdder(a= a[12], b= b[12], c= c11, sum= out[12], carry= c12);
    FullAdder(a= a[13], b= b[13], c= c12, sum= out[13], carry= c13);
    FullAdder(a= a[14], b= b[14], c= c13, sum= out[14], carry= c14);
    FullAdder(a= a[15], b= b[15], c= c14, sum= out[15], carry= c15);
}

这样的代码可以通过仿真测试，效果如下图所示 ⬇️

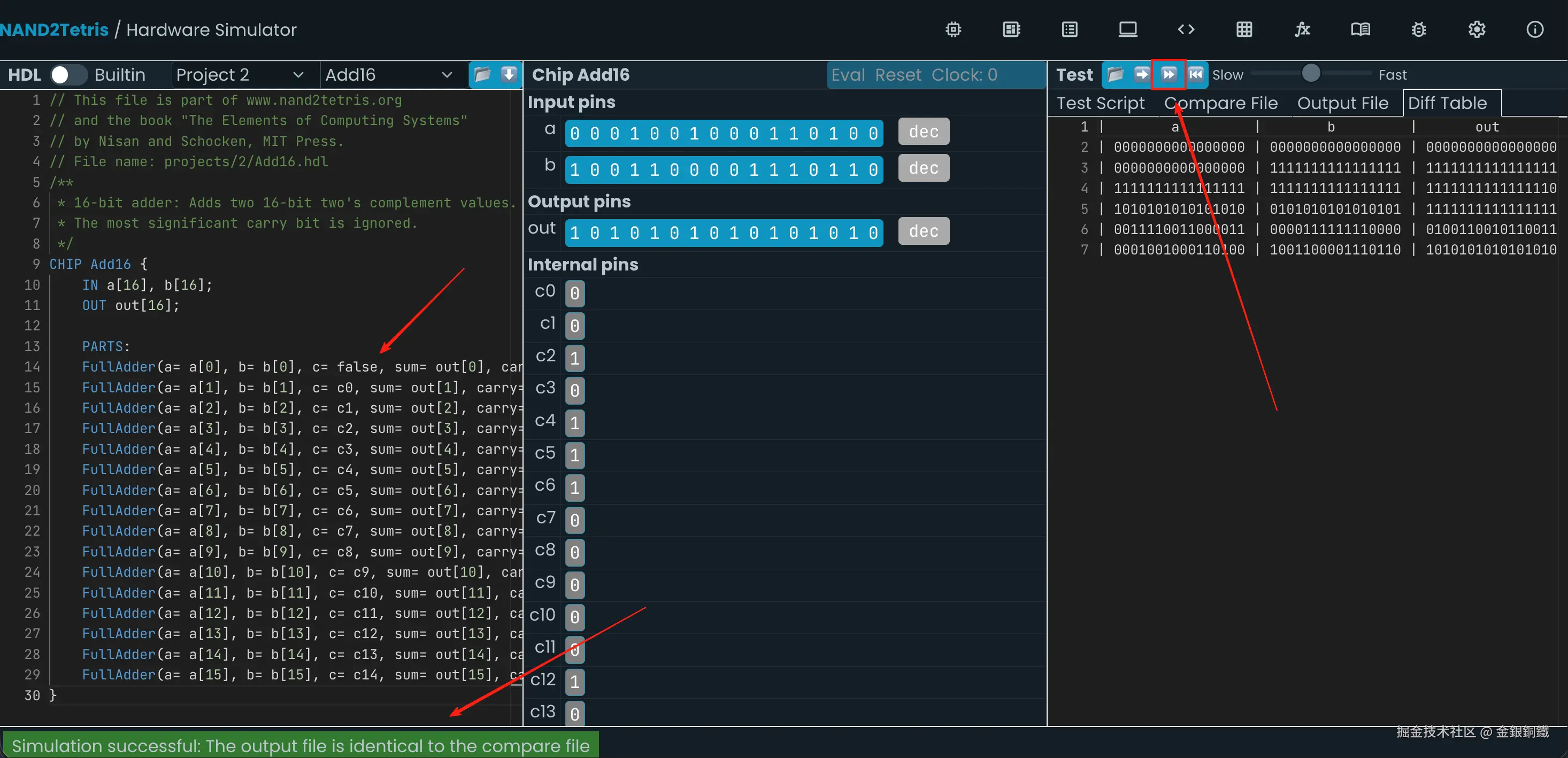
4. 实现 <math xmlns="http://www.w3.org/1998/Math/MathML"> 16 16 </math>16 位自增器(`Inc16`)

前往 Nand to Tetris Online IDE，选择 Project 2 里的 Inc16，效果如下图所示 ⬇️

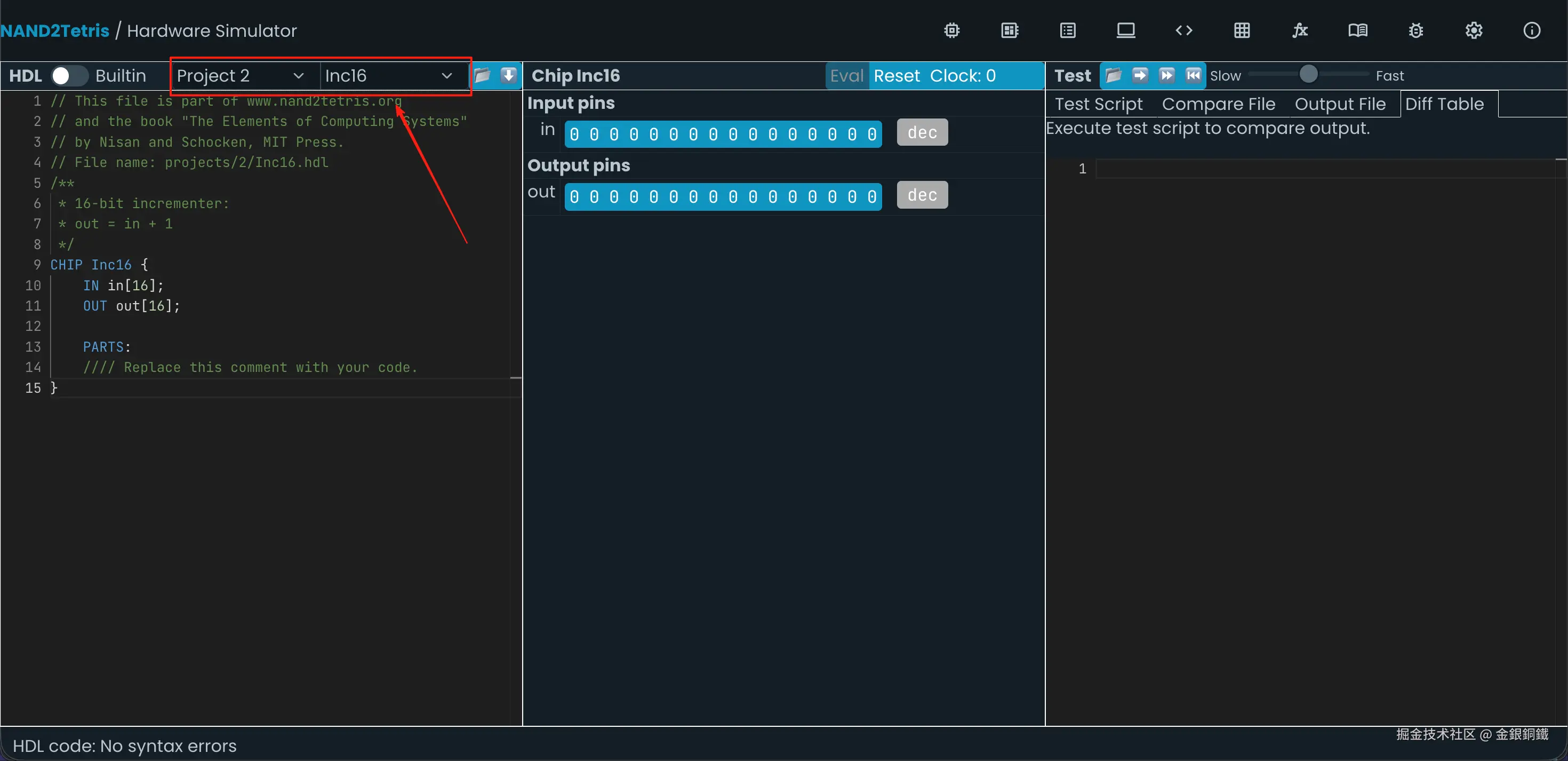
我们的目标是用 Project 1 里已经实现的各种 chip，以及刚才实现的 HalfAdder/FullAdder/Add16 来实现一个 Inc16。

输入是
- <math xmlns="http://www.w3.org/1998/Math/MathML"> i n [ 16 ] in[16] </math>in[16]
输出是
- <math xmlns="http://www.w3.org/1998/Math/MathML"> o u t [ 16 ] out[16] </math>out[16]

要实现的逻辑如下 ⬇️

text 复制代码

16-bit incrementer:
out = in + 1

一个直观的做法是使用上一步实现的 Add16，具体的代码如下 ⬇️

hdl 复制代码

CHIP Inc16 {
    IN in[16];
    OUT out[16];

    PARTS:
    Add16(a = in, b[0]= true, b[1..15] = false, out = out);
}

这样的代码可以通过仿真测试，效果如下图所示 ⬇️

5. 实现算术逻辑单元(`ALU`)

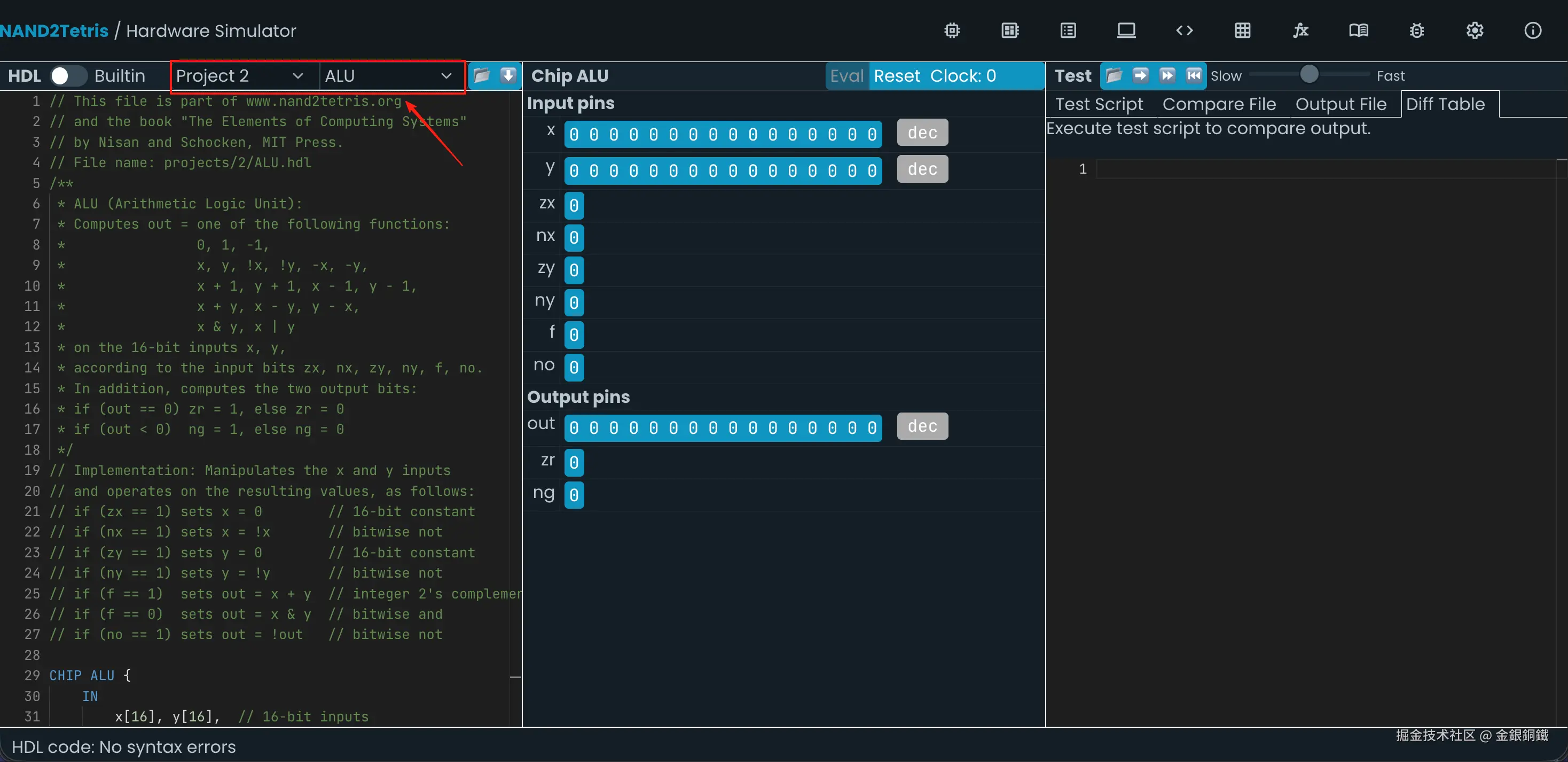
前往 Nand to Tetris Online IDE，选择 Project 2 里的 ALU，效果如下图所示 ⬇️

参考资料

Nand to Tetris Online IDE

From Nand to Tetris 里的 Project 2

背景

正文

1. 实现 HalfAdder

2. 实现 FullAdder

如何表示 <math xmlns="http://www.w3.org/1998/Math/MathML"> s u m sum </math>sum

如何表示 <math xmlns="http://www.w3.org/1998/Math/MathML"> c a r r y carry </math>carry

3. 实现 <math xmlns="http://www.w3.org/1998/Math/MathML"> 16 16 </math>16 位加法器(Add16)

4. 实现 <math xmlns="http://www.w3.org/1998/Math/MathML"> 16 16 </math>16 位自增器(Inc16)

5. 实现算术逻辑单元(ALU)

参考资料

1. 实现 `HalfAdder`

2. 实现 `FullAdder`

3. 实现 <math xmlns="http://www.w3.org/1998/Math/MathML"> 16 16 </math>16 位加法器(`Add16`)

4. 实现 <math xmlns="http://www.w3.org/1998/Math/MathML"> 16 16 </math>16 位自增器(`Inc16`)

5. 实现算术逻辑单元(`ALU`)