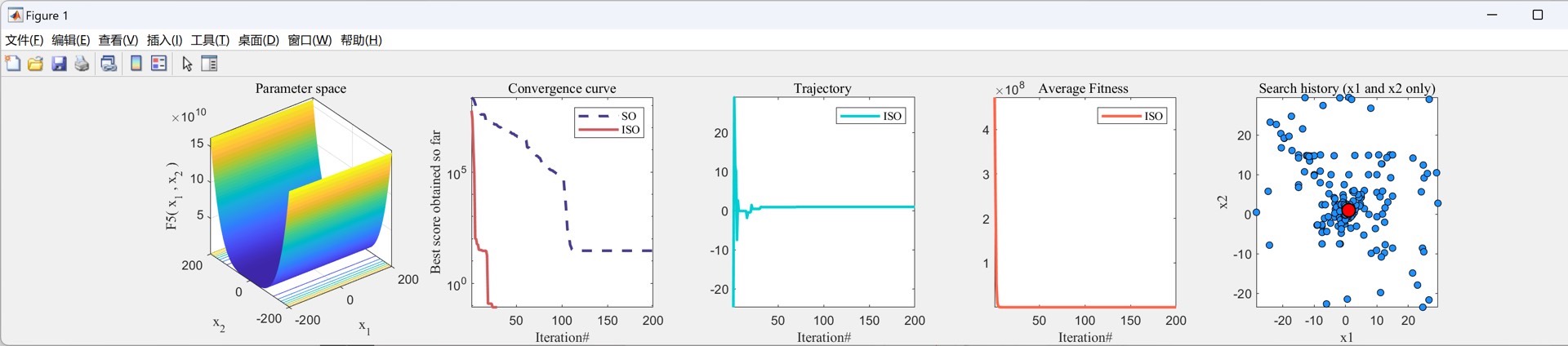
多策略增强型的改进蛇优化算法在Matlab中的实现与探讨

多策略增强型的改进蛇优化算法-- Matlab 三种策略的提出： 1、多策略混沌系统 2、反捕食策略 3、双向种群进化动力学运行效果如下，仅是代码无介绍

最近在研究优化算法的过程中，接触到了一种非常有意思的多策略增强型的改进蛇优化算法，今天就来和大家分享一下这个算法在Matlab中的实现以及其中涉及的三种关键策略。

三种策略解析

1. 多策略混沌系统

混沌系统在优化算法里常常能带来意想不到的效果。它可以产生看似随机但实则有规律的序列，帮助算法更好地在搜索空间中进行探索，避免陷入局部最优解。在我们的改进蛇优化算法里，多策略混沌系统的引入使得蛇在寻找猎物的过程中，能够以更加多样化的路径进行搜索。

matlab 复制代码

% 以Logistic混沌映射为例生成混沌序列
r = 3.9; % 混沌映射参数
x(1) = 0.5;
for i = 2:N
    x(i) = r * x(i - 1) * (1 - x(i - 1));
end

这段简单的Matlab代码实现了Logistic混沌映射，其中r是一个关键参数，不同的r值会产生不同特性的混沌序列。通过这种方式生成的混沌序列，可用于引导蛇优化算法中蛇的初始位置或移动方向等，让算法的搜索过程更加丰富。

2. 反捕食策略

自然界中被捕食者为了生存，会进化出各种反捕食策略。在算法里，这个策略模拟了蛇在面临被捕食威胁时的反应。想象一下，蛇在搜索猎物的同时，也要时刻警惕周围可能存在的危险。当检测到"危险"（比如算法中的某些参数满足一定条件）时，蛇会改变自身的搜索行为，可能会突然改变方向，或者暂时隐藏起来，避免被"捕食"。这样一来，算法就能跳出可能的局部最优陷阱，继续探索更优的解空间。

matlab 复制代码

% 假设存在一个危险检测函数
function isDanger = checkDanger(snakePosition, predatorPosition)
    distance = norm(snakePosition - predatorPosition);
    if distance < dangerThreshold
        isDanger = true;
    else
        isDanger = false;
    end
end

在上述代码中，checkDanger函数通过计算蛇和"捕食者"之间的距离来判断是否处于危险状态。一旦检测到危险，蛇优化算法中的蛇就会根据预设的反捕食规则改变行为，这为算法增加了一种自适应的搜索机制。

3. 双向种群进化动力学

传统的优化算法种群进化往往是单向的，而双向种群进化动力学则打破了这种常规。在蛇优化算法里，种群中的蛇不仅朝着更好的解的方向进化，同时也会从已经探索到的较好解中获取信息，反向影响种群的其他个体。这就好像蛇群之间有了一种双向的信息交流，一部分蛇发现了更好的猎物位置，会将信息传递给其他蛇，同时其他蛇的状态也会反馈回来，促进整体种群更加高效地进化。

matlab 复制代码

% 假设存在种群更新函数
function newPopulation = updatePopulation(population, bestSolution)
    % 正向进化部分
    for i = 1:populationSize
        % 根据bestSolution更新种群个体
        population(i) = population(i) + alpha * (bestSolution - population(i));
    end
    % 反向进化部分
    averageFitness = sum([population.fitness]) / populationSize;
    for i = 1:populationSize
        if population(i).fitness < averageFitness
            % 根据平均适应度反向调整种群个体
            population(i) = population(i) - beta * (population(i) - averageSolution);
        end
    end
    newPopulation = population;
end

上述代码展示了一个简单的双向种群更新思路，通过正向朝着最优解进化以及反向根据种群平均适应度调整个体，让种群在搜索空间中能够更全面地探索，提高找到全局最优解的概率。

运行效果展示

虽然这里仅提供代码无介绍，但实际运行这个多策略增强型的改进蛇优化算法时，我们可以看到它在处理复杂优化问题上相较于传统蛇优化算法有明显的优势。通过三种策略的协同作用，算法能够更快地收敛到更优的解，无论是在收敛速度还是解的质量上都有显著提升。

总的来说，这种多策略增强型的改进蛇优化算法在Matlab中的实现为我们解决优化问题提供了一种全新的思路和有力的工具。希望这篇博文能让大家对这个有趣的算法有更深入的了解，也欢迎大家一起探讨在实际应用中的更多可能性。