十、工具变量法 stata 演示 （mac）

参考 陈强教授 《计量经济学与Stata应用》使用 grilic.dta 数据集 （陈强教授官网开源）

1.OLS回归

reg lnw s expr tenure rns smsa,r
# r表示使用异方差强健的标准误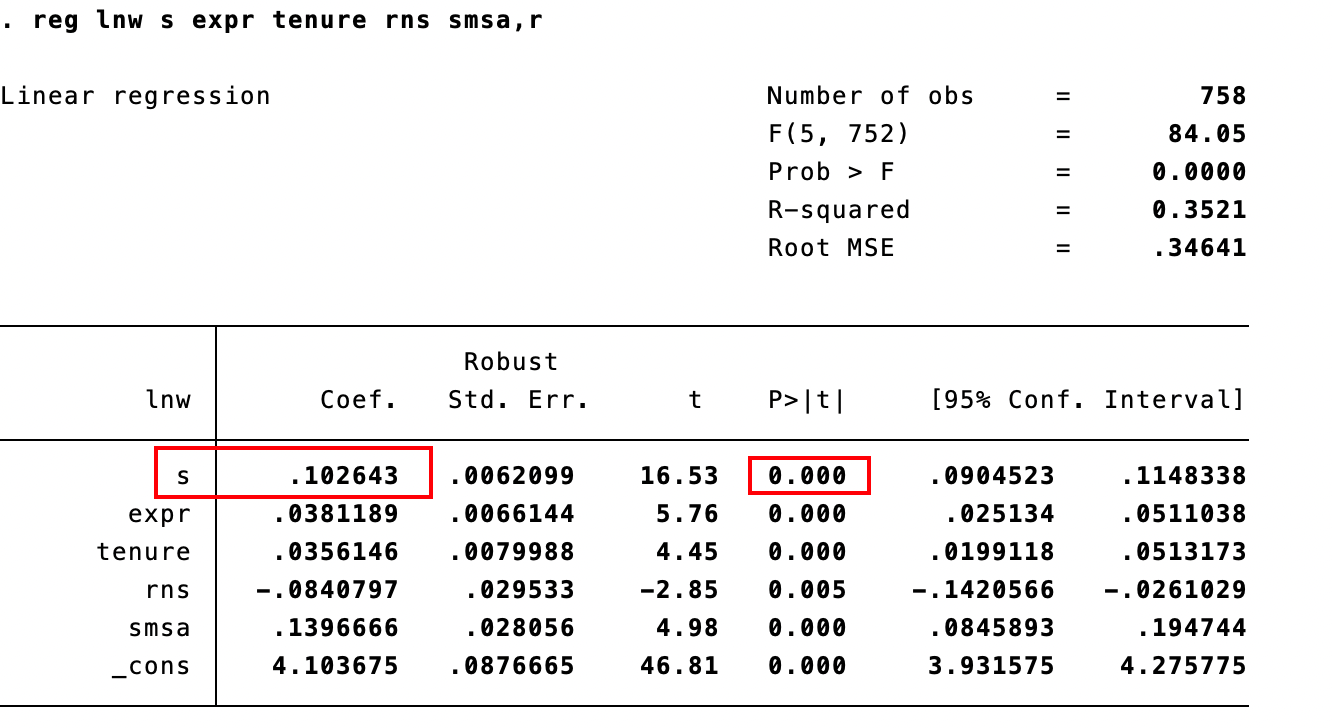

s 产生的效果太大了，遗漏变量iq

2.带上iq的OLS回归

reg lnw iq s expr tenure rns smsa,r
# r表示使用异方差强健的标准误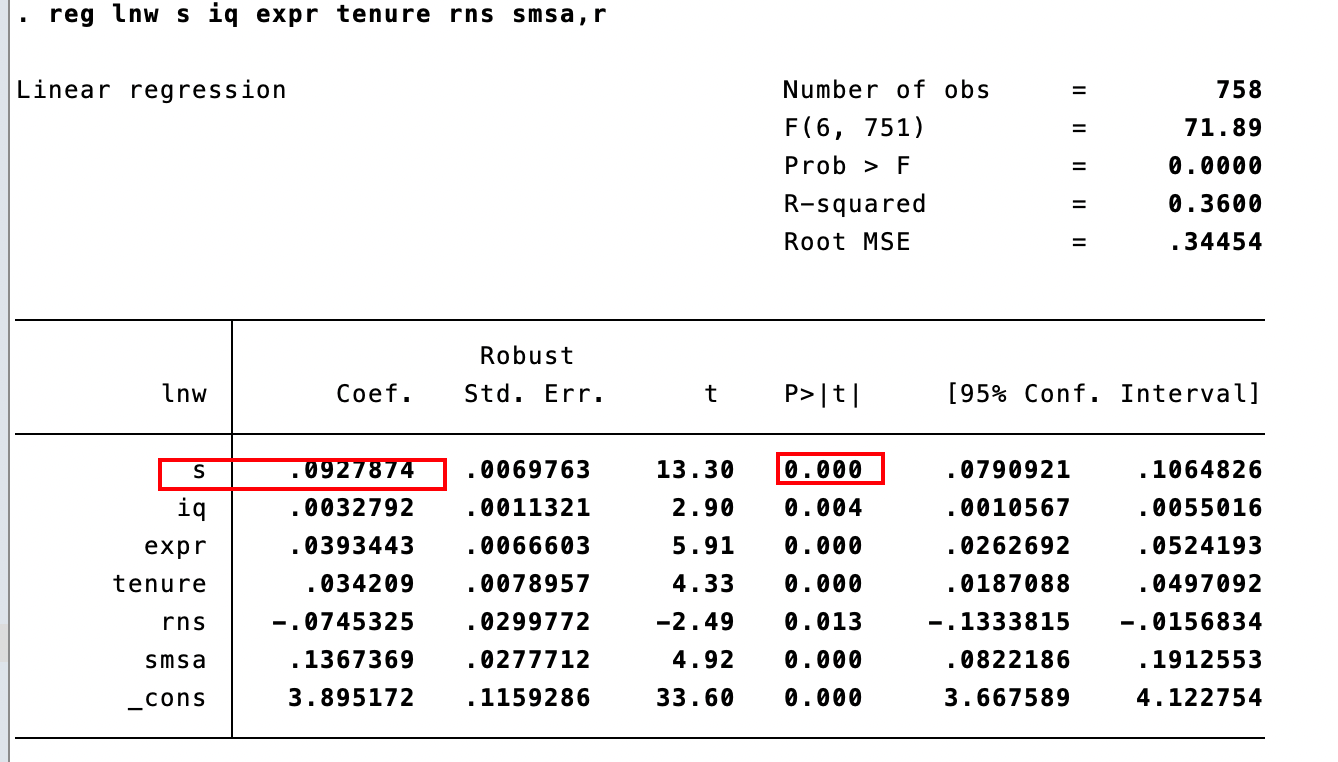

还是有点大，存在内生性问题->使用IV

3.工具变量法 IV

如果你使用ivreghdfe命令则需要自己手动安装ivreghdfe

安装命令

cap ado uninstall reghdfe # 刚下载的stata可以不执行

cap ado uninstall ivreghdfe # 刚下载的stata可以不执行

net install ftools, from(/Applications/Stata/ivreghdfe安装包/ftools-master/src)

net install reghdfe, from(/Applications/Stata/ivreghdfe安装包/reghdfe-master/src)

net install ivreghdfe, from(/Applications/Stata/ivreghdfe安装包/ivreghdfe-master/src)

（）中为你自己的文件路径，直到src

我是mac so / ; if windows \

补充： mac 一键复制绝对路径命令： option+command+c

参考资料：压缩包下载

在这下载即可

ivregress 2sls lnw s expr tenure rns smsa (iq=med kww),r first
# r 同robust 表示使用异方差强健的标准误
# 注意smsa后空一格，不然报错r（132）：parentheses unbalanced

#  ivreghdfe lnw s expr tenure rns smsa (iq=med kww)

# 常用的ivreghdfe也可以得出结果，但是后续的过度检验无法进行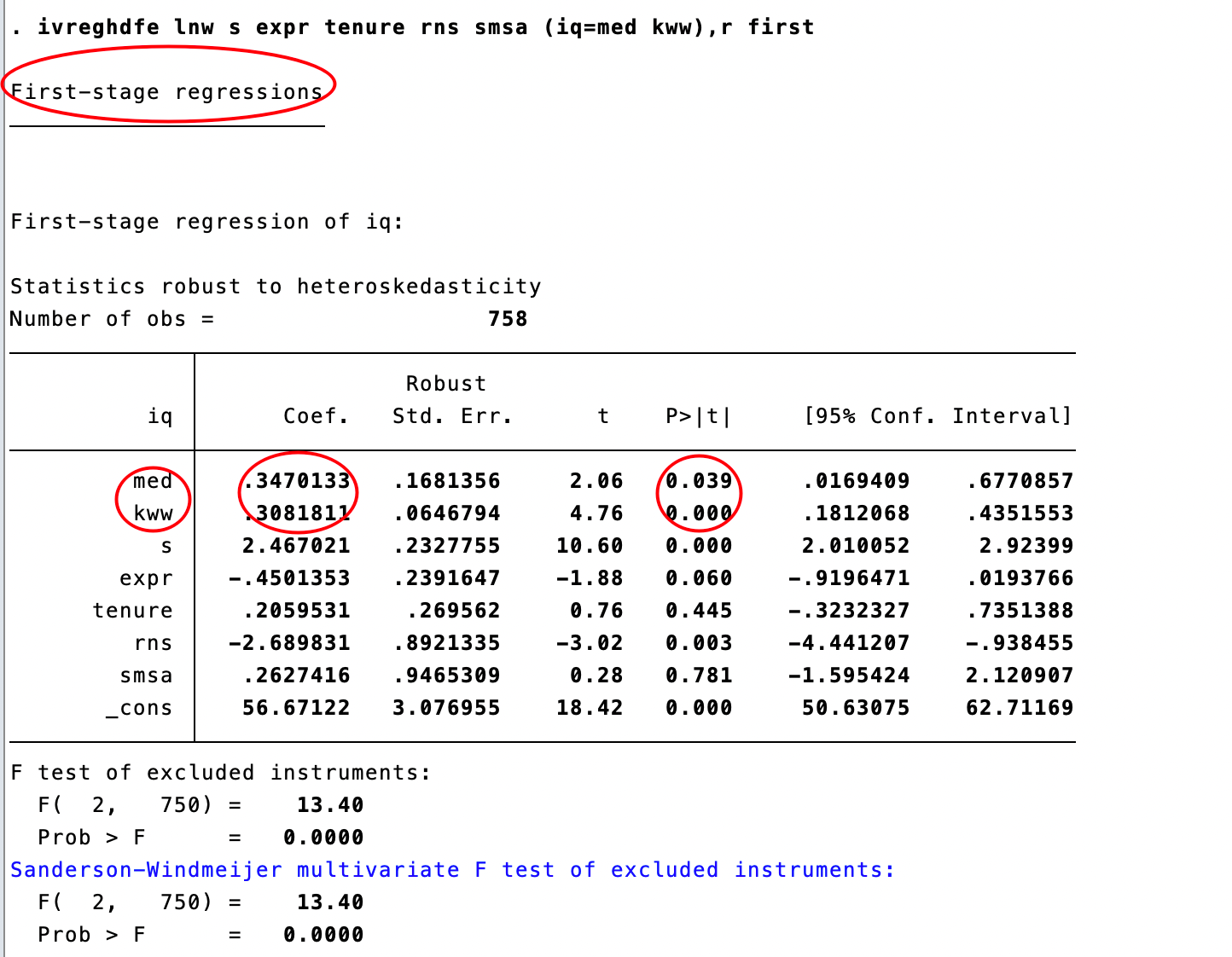

表示med kww都和iq 正相关，med p值 <0.5表示在95%的置信度下显著 kww 在99.9%下都显著

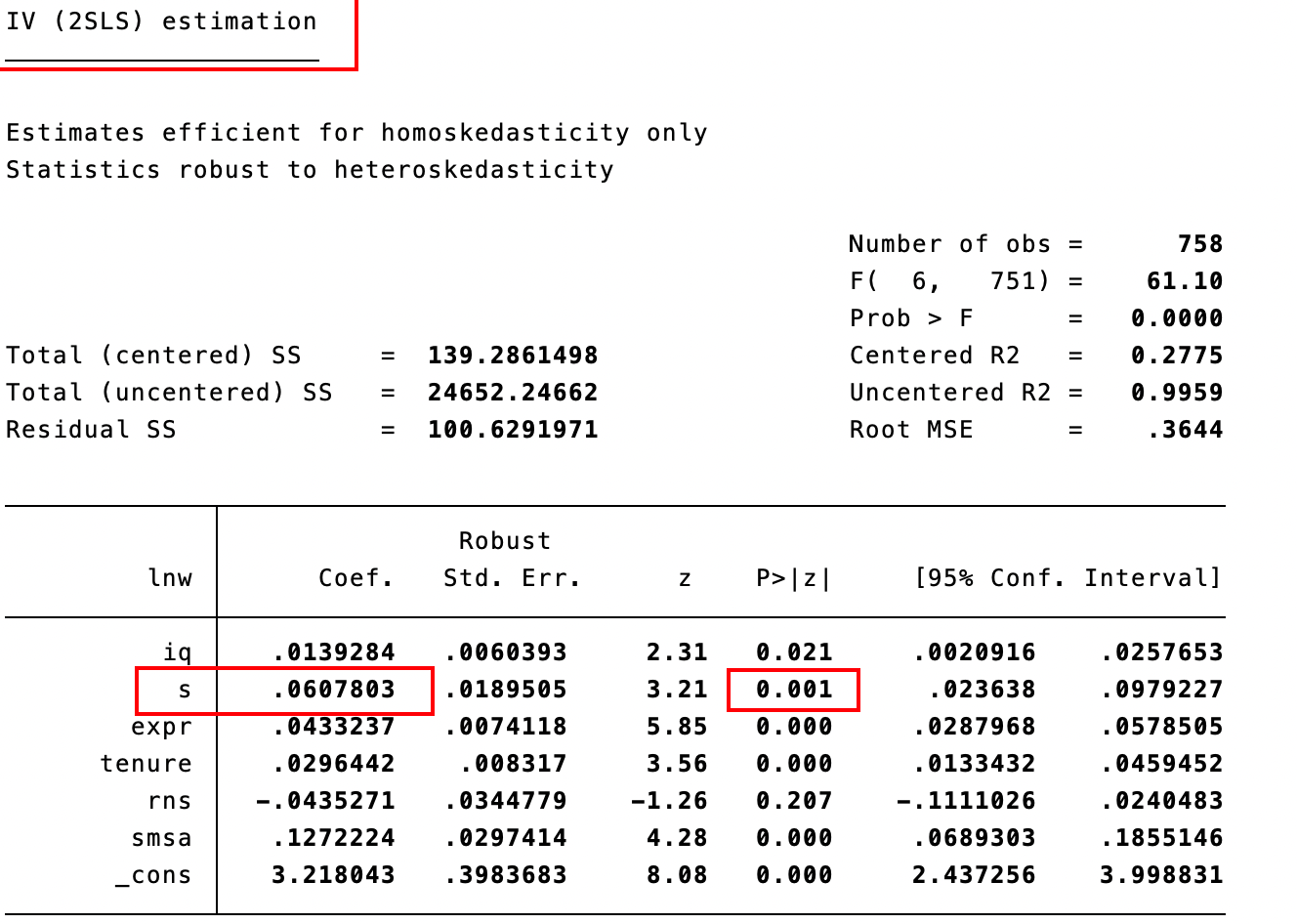
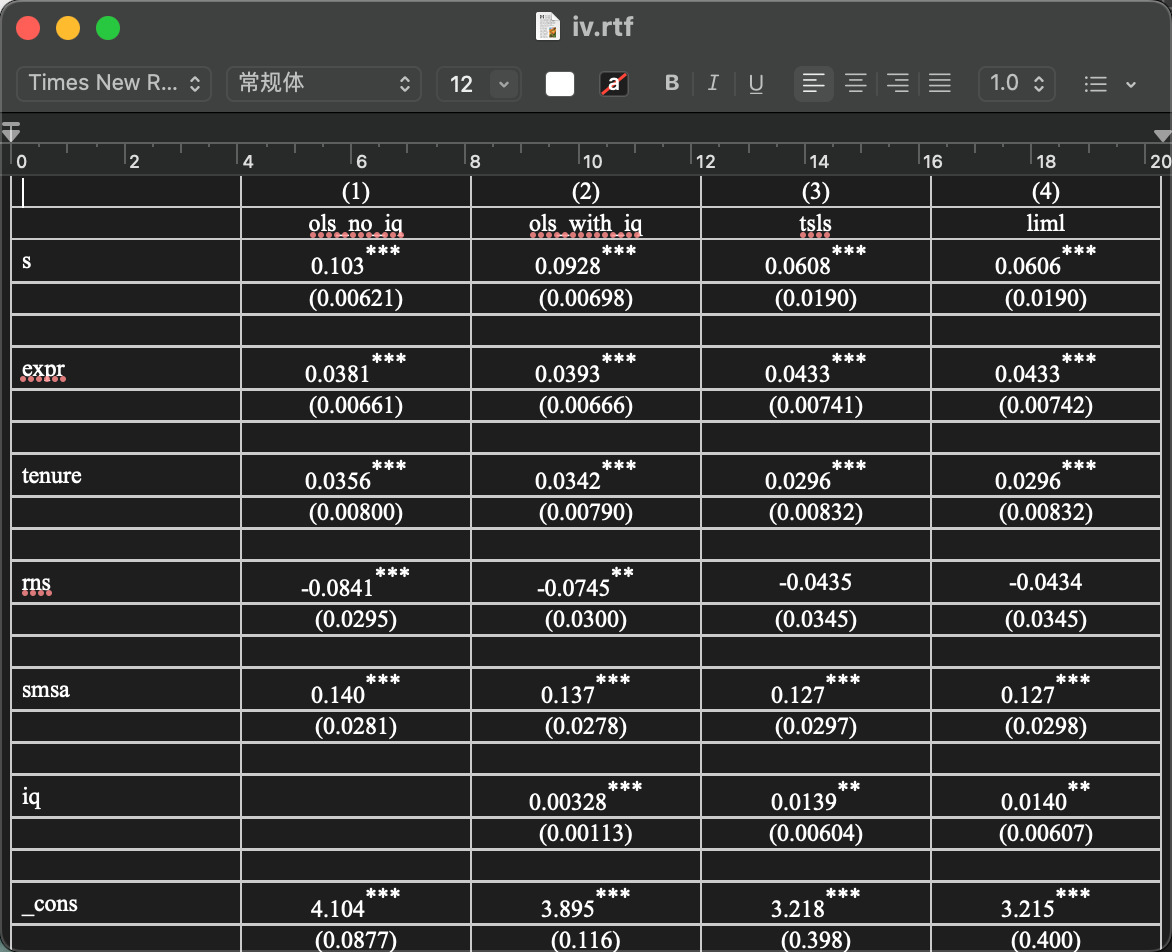
此时表示s贡献率6.08%，合理，在99.9%的置信度下可靠

4.检验外生性 过度检验

estat overid

p> 0.05,接受原假设，(med,kww)外生

5.检验内生性

quietly ivregress 2sls lnw s expr tenure rns smsa (iq=med kww)
# quietly 表示仅存储结果不显示

estat firststage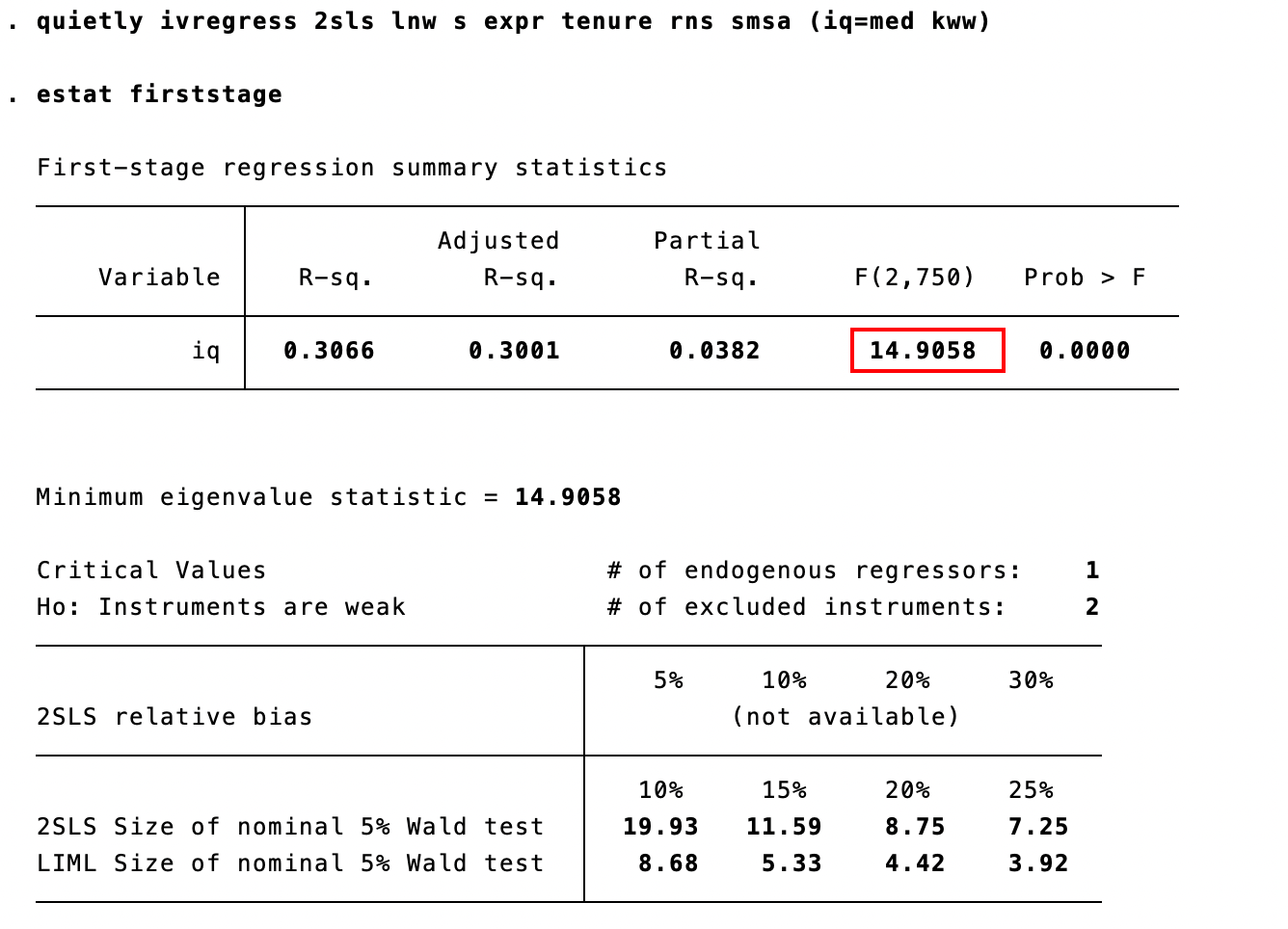

F > 10 ,故不存在弱工具变量

5+. 弱工具变量的解决方法 LIML 有效信息最大似然估计法

ivregress liml lnw s expr tenure rns smsa (iq=med kww),r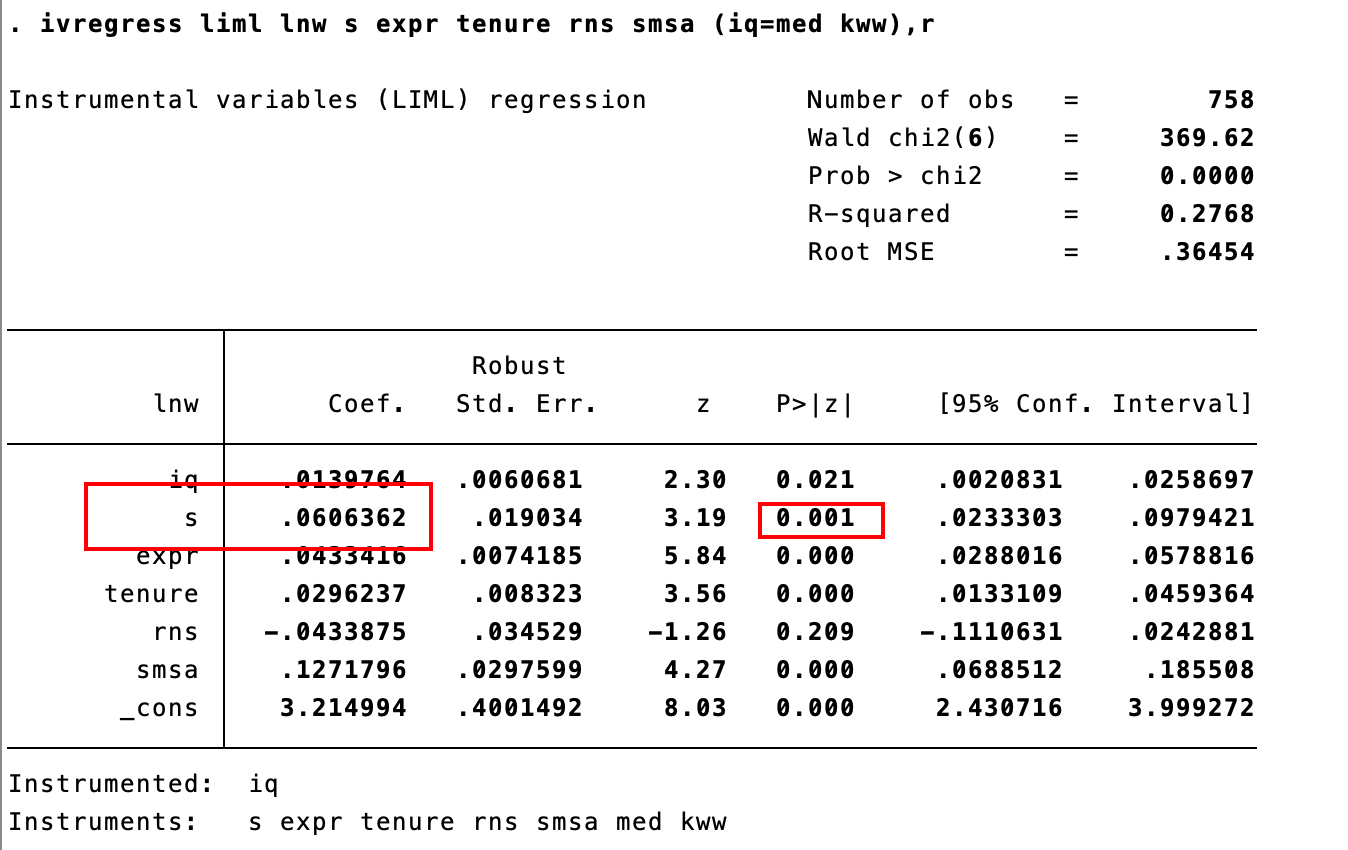

结果与2sls接近，so证明无弱工具变量

6.检验解释变量是否存在内生变量

# 比较ols 和 2sls的 差别 if p<0.05 则拒绝H0:所有解释变量均外生
quietly reg lnw iq s expr tenure rns smsa 

estimates store ols

quietly ivregress 2sls lnw s expr tenure rns smsa (iq=med kww)

estimates store iv

hausman iv ols,constant sigmamore 

# constant 表示 ols 和iv中均存在常数项
# sigmamore 表示使用效率高的，若同方差则 使用ols（此时iv = ols） ，异方差 iv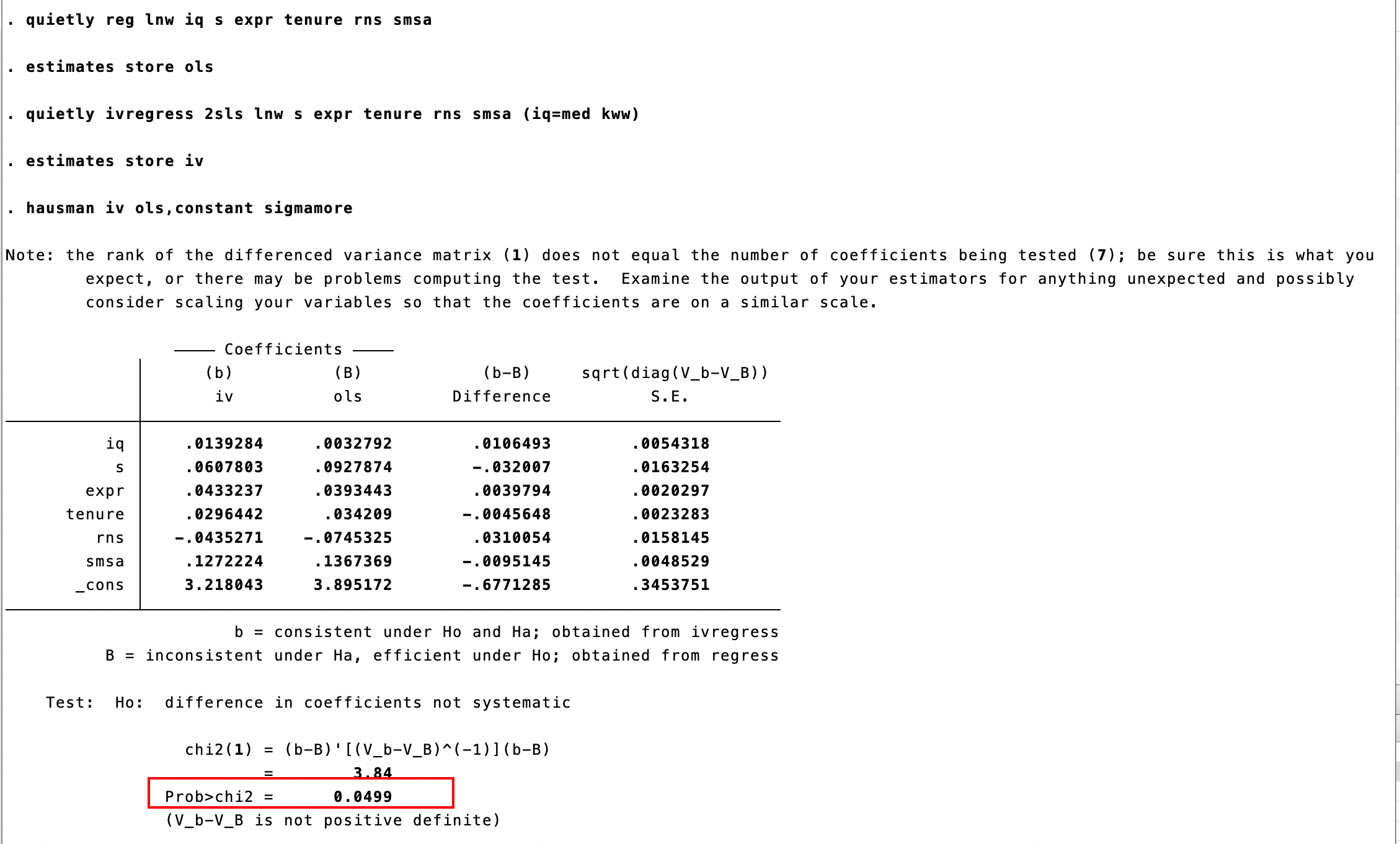

p < 0.05 ，则拒绝原假设，则解释变量中存在内生变量

ATTN\] 豪斯曼检验仅适用于同方差，异方差适用杜宾-吴-豪斯曼检验 DWH ### 6+. DWH 检验 estat endogenous 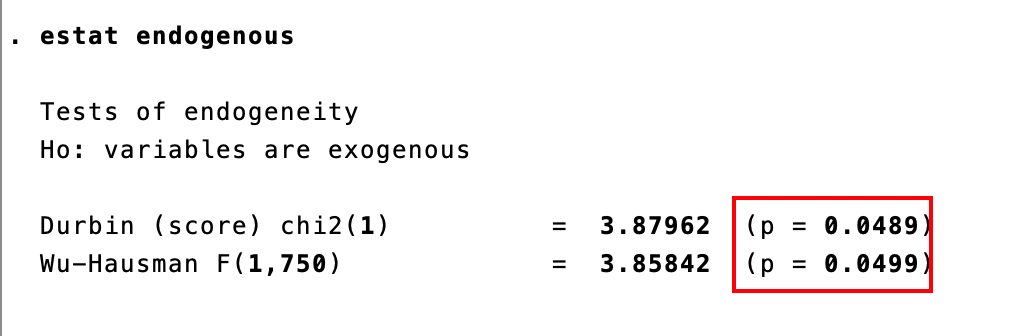 p\<0.05，则存在内生性解释变量，即iq ## 7.存储结果于一个表格中并显示显著性，用在论文结果展示中 esttab ols_no_iq ols_with_iq tsls liml,se r2 mtitle star (* 0.1 ** 0.05 *** 0.01) # 需要提前安装estout # ssc install estout # se 表示在括弧中显示标准误(默认使用t统计量，p 则显示p值) # r2 即R^2 # mtitle （model title）表示 使用模型名称作为列标题 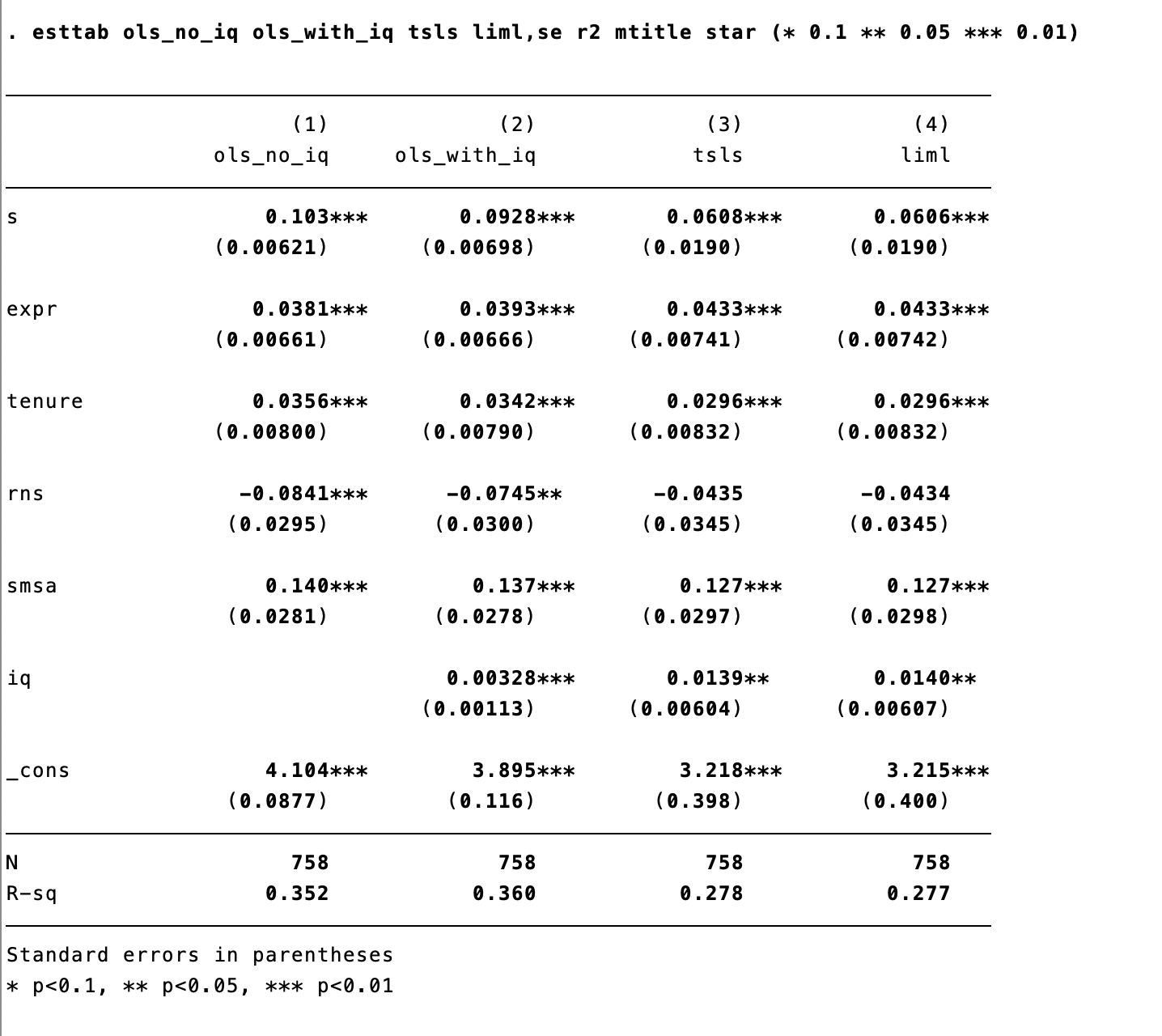 7+.输出word esttab ols_no_iq ols_with_iq tsls liml using iv.rtf,se r2 mtitle star (* 0.1 ** 0.05 *** 0.01) # 添加 using iv.rtf rtf - rich text format  点击此处即可显示rtf文件，可以复制到word中