为什么要 Re-ranking
"re-ranking(重排序)" 是信息检索流程中非常关键的步骤,核心目的是弥补初步召回阶段的不足,提升最终结果的相关性与用户体验。
初步召回阶段的天然缺陷
传统检索的第一步(初步召回)通常依赖基于词项的模型(如 BM25、TF-IDF),这类方法的局限性很明显:
只能做 "词项匹配",无法理解语义:
比如查询 "苹果的系统",初步召回可能会混入 "水果苹果" 的文档,因为它只看关键词是否出现,不懂 "苹果" 的语义歧义
无法捕捉细粒度关联:
比如查询 "如何用 Python 实现快速排序",初召可能优先返回包含 "Python"、"排序" 但内容不相关文档,无法识别 "实现快速排序" 具体需求
召回结果数量大、质量参差不齐:
为了保证 "不漏掉相关文档",初步召回通常会返回几百甚至上千个候选,但其中大部分是低相关度的内容
重排序的核心价值
重排序正是为了解决上述问题,通过更精准的模型(通常是神经模型) 对初步召回的候选文档再筛选、排序:
-
提升语义匹配精度:用 ColBERT、BERT 这类模型,能理解查询与文档的上下文语义(比如区分 "苹果" 不同含义),找到真正相关内容
-
优化排序合理性:把 "最符合用户需求" 的文档排到前面,避免用户翻很多页才能找到有效信息
-
平衡效率与效果:初召用低成本的词项模型快速捞取候选,重排序用高成本的精准模型处理少量候选 ------ 保证检索速度提升结果质量
Top-k Re-ranking with ColBERT 基于 ColBERT 的 Top-k 重排序
https://arxiv.org/pdf/2004.12832
原文介绍如下
Recall 回忆
Recall that ColBERT can be used for re-ranking the output of another retrieval model, typically a term-based model, or directly for end-to-end retrieval from a document collection. In this section, we discuss how we use ColBERT for ranking a small set of k (e.g., k=1000) documents given a query q. Since k is small, we rely on batch computations to exhaustively(穷举式) score(打分) each document (unlike our approach in §3.6). To begin with(首先), our query serving subsystem loads the indexed documents representations into memory, representing each document as a matrix of embeddings.
ColBERT 既可以用于对其他检索模型(通常是基于词项 term-based 的模型)的输出结果进行重排序,也可以直接用于从文档集合中进行端到端检索。在本节中,将介绍如何利用 ColBERT 对查询 q 对应的少量(例如k=1000)文档进行排序。由于 k 的数值较小,可以通过批量计算来对每个文档进行穷举式打分(这与 3.6 节中的方法不同)。首先,我们的查询服务子系统会将已索引的文档表示加载到内存中,每个文档都以一个嵌入矩阵的形式存储。
(个人理解:简述测试步骤)
Given a query q, we compute its bag of contextualized embeddings Eq (Equation 1) and, concurrently, gather the document representations(表示) into a 3-dimensional tensor D consisting of k document matrices. We pad the k documents to their maximum length to facilitate batched operations, and move the tensor D to the GPU's memory. On the GPU, we compute a batch dot-product of Eq and D, possibly over multiple mini-batches. The output materializes a 3-dimensional tensor that is a collection of cross-match matrices(交叉匹配矩阵) between q and each document. To compute the score of each document, we reduce its matrix across document terms via a max-pool(最大池化) (i.e., representing an exhaustive implementation of our MaxSim computation) and reduce across query terms via a summation. Finally, we sort the k documents by their total scores.
representations ˌreprɪzenˈteɪʃ(ə)n n. 代理人,代表;描绘,表现;表示,象征;表现物(尤指画或模型);<正式>抗议,陈述;表象
facilitate fəˈsɪlɪteɪt v. 使更容易,使便利;促进,推动
materialize məˈtɪəriəlaɪz
v. 实现,成为现实;突然显现,奇怪地出现
v.使具体化;使实现;使物质化:使某事物从想法、计划或无形状态变为现实、具体或有形状态。
summation sʌˈmeɪʃ(ə)n n. 和;[生理] 总和;合计
给定查询q,先计算其上下文嵌入集合Eq(对应公式 1),同时将 k 个文档的表示整合为一个三维张量 D(包含 k 个文档矩阵)。我们会将这 k 个文档填充至其最大长度,以便进行批量操作,并将张量 D 转移至 GPU 内存。在 GPU 上,计算 Eq 与 D 的批量点积(必要时可分多个小批量进行),输出结果是一个三维张量,包含查询 q 与每个文档之间的交叉匹配矩阵。为了计算每个文档的得分,我们通过最大池(即,表示我们的MaxSim计算的详尽实现)降维矩阵(across document terms,沿着doc terms),并通过求和降低(across query terms,沿着query terms)。最后,我们根据总分对这 k 个文档进行排序。
(个人理解:计算步骤)
quadratic kwɒˈdrætɪk
adj. [数] 二次的
n. 二次方程式
Relative to existing neural rankers (especially, but not exclusively, BERT-based ones), this computation is very cheap that, in fact, its cost is dominated by the cost of gathering and transferring the pre-computed embeddings. To illustrate, ranking k documents via typical BERT rankers requires feeding BERT k different inputs each of length l=∣q∣+∣di∣ for query q and documents di, where attention has quadratic(平方级的)cost in the length of the sequence. In contrast, ColBERT feeds BERT only a single, much shorter sequence of length l=∣q∣. Consequently, ColBERT is not only cheaper, it also scales much better with k as we examine in §4.2.
illustrate ˈɪləstreɪt v. 加插图于;说明,阐明;证明,证实
feed fiːd
v. 饲养,喂养,为......提供食物;以......为食物,吃食;提供(意见或信息等),灌输;施肥;添加燃料;把......放进机器,将......塞进机器;加深,强化;使(缓慢平稳地)移动,使穿过(有限的空间);<非正式>维持,满足(习惯);传球;流入,进入
n. 哺乳,喂养;动物的饲料,植物的肥料;(机器的)进料装置;(机器、设备的)原料供给;(卫星或网络)转播,(信号)传输;(计算机)订阅源;(给舞台演员的)提词,提白;<非正式>丰盛的一餐
与现有的神经排序模型(尤其是但不限于基于 BERT 的模型)相比,这种计算的成本非常低 ------ 实际上,其成本主要来自预计算嵌入的获取与传输。举例来说,典型的 BERT 排序模型对 k 个文档进行排序时,需要将 BERT 输入k 个不同的序列(每个序列长度为 l=∣q∣+∣di∣,即查询 q 与文档 di 的长度之和),而注意力机制的成本与序列长度呈平方级关系。相比之下,ColBERT 仅需将 BERT 输入一个长度为 l=∣q∣
的更短序列。因此,ColBERT 不仅成本更低,且随着 k 的增大,其扩展性也显著更优(我们会在 4.2 节展开分析)。
(个人理解:讲对比)
end-to-end retrieval(端到端检索)
信息检索领域的一种技术范式,指从 "接收查询" 到 "返回最终结果" 的全流程由一个统一的模型 / 系统直接完成,无需依赖多阶段的 "初步召回 + 重排序" 等步骤
流程简化:传统检索通常分两步 ------ 先用基于词项的模型(如 BM25)召回大量候选文档,再用神经模型重排序;而端到端检索则直接通过模型(如 ColBERT)从全量文档集合中筛选出最相关的结果,无需中间候选集。
语义驱动:依赖模型的上下文语义理解能力(而非单纯的词项匹配),能直接捕捉查询与文档的细粒度语义关联。
效率与精度平衡:像 ColBERT 这类端到端检索模型,通过预计算文档嵌入、延迟交互等机制,既保留了神经模型的精度,又能高效处理大规模文档集合。
举个例子:当输入 "人工智能的应用场景",端到端检索模型会直接从整个文档库中,基于语义匹配选出最相关的内容并排序,而不是先靠关键词捞出几百篇再二次筛选。
matrix across document terms
To compute the score of each document, we reduce its matrix across document terms via a max-pool(最大池化) (i.e., representing an exhaustive implementation of our MaxSim computation) and reduce across query terms via a summation. Finally, we sort the k documents by their total scores.
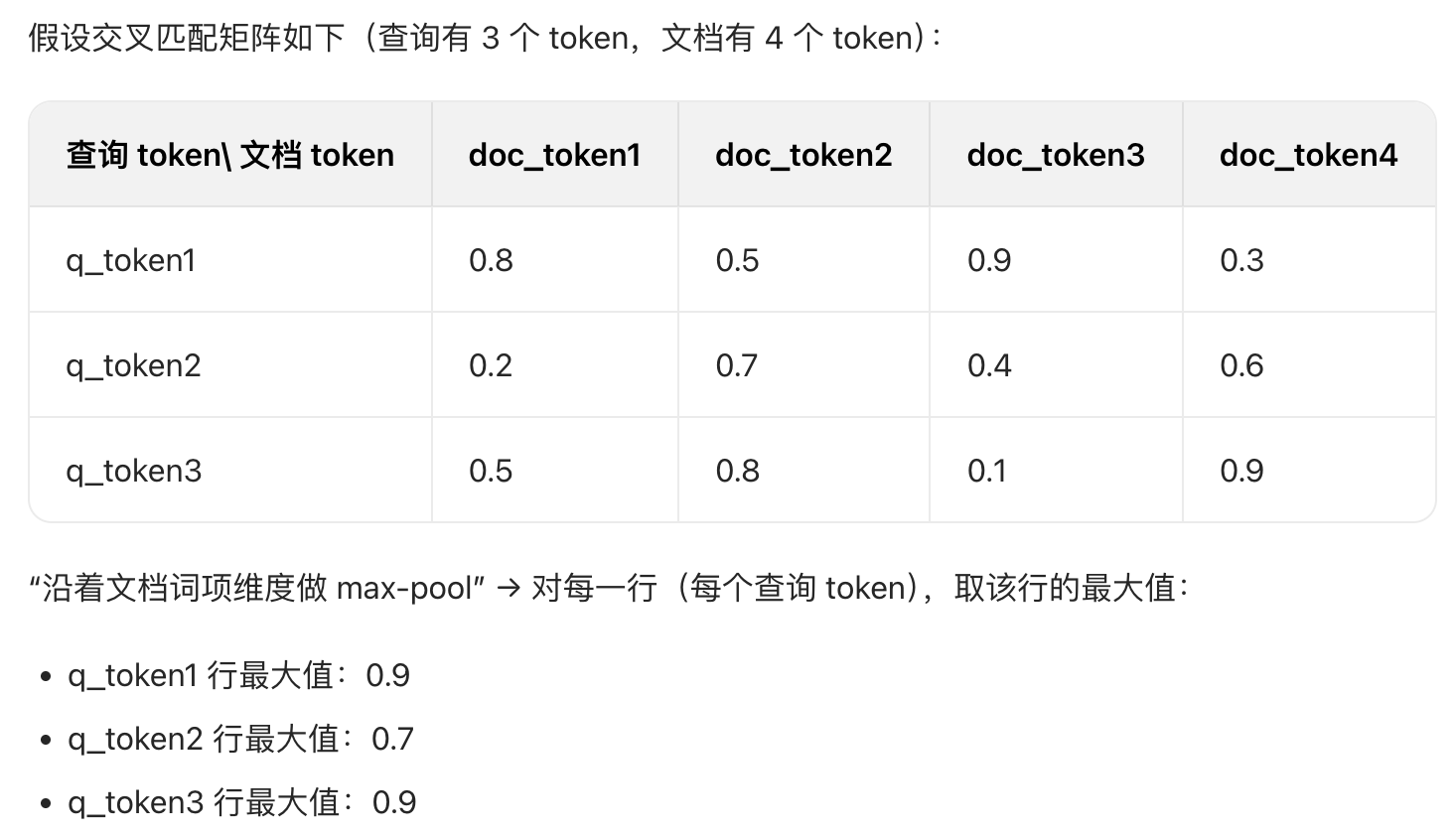
这个操作是 ColBERT "延迟交互" 的关键一步:先通过矩阵保留查询与文档所有 token 的细粒度匹配信息,再通过 max-pool 聚焦 "最相关" 的匹配关系,既保留语义精度,又完成维度压缩,为后续 "对查询词项维度求和"(得到最终文档得分)做准备。
倒排融合(Reciprocal Rank Fusion,RRF)
Reciprocal rɪˈsɪprək(ə)l
adj. 相互的,互惠的,报答的;(路线,方向)反向的;(代词,动词)互相的;(量,函数)倒数的;互逆的,互反的
n. 反身代词,相互动词; 倒数,乘法逆元素;互相起作用的事物
RRF 是检索领域主流的无参数融合算法,无需训练即可平衡不同数据源的排序差异,适配性极强。

py
def reciprocal_rank_fusion(
recall_results: dict,
k: int = 60,
top_n: int = 100
) -> list:
"""
倒排融合多数据源的召回结果
Args:
recall_results: 各数据源的召回结果,格式为 {数据源名称: [文档id列表]},列表按相关性降序排列
k: 平滑参数,经验值60,值越小对排名越敏感
top_n: 最终返回的融合后top-N文档数量
Returns:
融合后的文档列表,格式为 [(文档id, 融合得分), ...],按得分降序排列
"""
# 初始化文档得分字典
doc_score = {}
# 遍历每个数据源的召回结果,计算倒排得分
for source_name, doc_list in recall_results.items():
# 遍历该数据源下的文档,记录排名(从1开始)
for rank, doc_id in enumerate(doc_list, start=1):
# 累加倒排得分
if doc_id not in doc_score:
doc_score[doc_id] = 0.0
doc_score[doc_id] += 1.0 / (k + rank)
# 按融合得分降序排序
sorted_docs = sorted(
doc_score.items(),
key=lambda x: x[1],
reverse=True
)
# 返回top-N结果
return sorted_docs[:top_n]
# -------------------------- 示例:测试倒排融合算法 --------------------------
if __name__ == "__main__":
# 模拟多数据源召回结果(实际场景可替换为BM25/ColBERT/ES等不同来源的召回列表)
recall_data = {
"BM25召回": ["doc_001", "doc_003", "doc_002", "doc_005", "doc_004"],
"ColBERT召回": ["doc_002", "doc_001", "doc_004", "doc_003", "doc_006"],
"ES向量召回": ["doc_001", "doc_002", "doc_006", "doc_005", "doc_003"]
}
# 执行倒排融合
fusion_result = reciprocal_rank_fusion(
recall_results=recall_data,
k=60,
top_n=5
)
# 打印结果
print("融合后Top5文档(文档ID | 融合得分):")
for idx, (doc_id, score) in enumerate(fusion_result, start=1):
print(f"第{idx}名:{doc_id} | {score:.4f}")代码说明
recall_results:支持任意数量的数据源,键为数据源名称(便于溯源),值为按相关性降序的文档 ID 列表
k:平滑参数,可根据业务场景调整(如对排名更敏感可减小至 30,更平缓则增大至 100)
top_n:控制最终返回的文档数量,适配检索系统的候选集大小
核心逻辑:
遍历每个数据源的召回列表,按排名计算倒排得分并累加
对所有文档的总得分降序排序,返回 Top-N 结果
示例输出:
plaintext
融合后Top5文档(文档ID | 融合得分):
第1名:doc_001 | 0.0487
第2名:doc_002 | 0.0484
第3名:doc_003 | 0.0322
第4名:doc_006 | 0.0164
第5名:doc_005 | 0.0163适配真实场景:
若召回结果包含相关性分数(而非仅排名),可先将分数转为排名(降序排序后取索引 + 1);
若文档 ID 为复杂结构(如包含标题 / 内容),可将doc_id替换为文档对象,仅需保证唯一标识即可。
性能优化:
当数据源 / 文档量极大时,可通过pandas向量化计算得分,替代字典遍历;
对每个数据源的召回列表做长度限制(如仅取前 1000 条),减少计算量。
多策略融合:
可在 RRF 基础上增加数据源权重(如对 ColBERT 结果乘以 1.2,BM25 乘以 0.8),适配不同数据源的可信度:
python
# 扩展:给不同数据源加权重
source_weights = {"BM25召回": 0.8, "ColBERT召回": 1.2, "ES向量召回": 1.0}
doc_score[doc_id] += source_weights[source_name] / (k + rank)该代码可直接集成到检索系统的 "召回 - 融合 - 重排序" 流程中,是工业界最常用的多源召回融合方案之一
重排模块的探索方向:知识增强的重排、跨模态重排、个性化动态重排、重排过程的可解释性
当前 RAG 系统中重排技术的核心演进方向,它们分别从信息维度拓展、模态适配、用户定制和可信度提升四角度解决传统重排的局限性:
知识增强的重排
核心痛点
传统重排模型(如 ColBERT、BERT-reranker)仅依赖查询和文档的上下文语义匹配,缺乏领域知识、常识或结构化知识,容易在专业场景(如医疗、法律、金融)中出现 "语义匹配但事实错误" 的问题。
核心思路
将外部知识(包括结构化知识图谱、领域知识库、常识库)融入重排模型,让模型在计算相关性时同时考量 "语义匹配" 和 "事实一致性 / 知识合理性"。
落地路径
知识注入编码阶段:在 BERT/LLM 的编码层加入知识图谱的实体 / 关系嵌入,例如将文档中的实体链接到知识图谱,再将实体的知识向量与文本嵌入融合,提升编码的知识丰富度。
知识引导的损失函数:在训练重排模型时,增加 "事实一致性损失",若文档存在与领域知识冲突的内容,降低其排序得分。
知识检索辅助:重排前先检索相关知识片段,将知识与查询、文档拼接为新的输入,让模型基于 "查询 + 文档 + 知识" 进行综合判断。
典型应用
医疗领域 RAG 中,重排模型不仅匹配 "症状描述" 的语义,还会结合医学知识库判断文档中的治疗方案是否符合临床指南,优先排序合规且相关的内容。
跨模态重排
核心痛点
传统重排仅处理文本类召回结果,但实际 RAG 系统会涉及多模态数据(如图片、表格、音频转写、PDF 中的图表),单一文本重排模型无法适配跨模态的相关性判断。
核心思路
构建跨模态重排模型,支持对不同模态的候选内容(文本、图片、表格等)统一打分,实现 "多模态召回结果" 的一体化排序。
落地路径
多模态统一编码器:采用 CLIP、ColPali 等模型,将文本查询和不同模态的文档转为统一语义空间的嵌入,再通过 MaxSim 等方式计算跨模态相关性。
模态适配的交互机制:对表格类数据,先通过表格理解模型提取结构化信息;对图片,先通过图文模型生成描述文本,再结合原始模态特征与文本特征进行联合重排。
多模态混合排序策略:为不同模态设置适配的子重排器(如文本子重排器、表格子重排器),再通过融合层(如 RRF、加权投票)输出最终排序。
典型应用
教育 RAG 系统中,用户查询 "牛顿第二定律的实验示意图",重排模型可同时对文本解释、实验表格、示意图图片进行跨模态打分,优先返回示意图和配套文本说明。
个性化动态重排
核心痛点
传统重排模型是 "全局统一" 的,对所有用户返回相同排序逻辑的结果,但不同用户的知识背景、需求偏好、使用场景存在差异(如新手用户需要基础内容,专家用户需要深度文献),统一排序无法满足个性化需求。
核心思路
基于用户画像 / 上下文动态调整重排策略,让排序结果适配单个用户的独特需求,实现 "千人千面" 的重排效果。
落地路径
用户画像驱动的权重调整:构建用户画像(包括领域知识水平、历史点击偏好、职业标签等),动态调整重排模型的特征权重(如对新手用户提升 "易理解性" 特征权重,对专家用户提升 "专业性" 特征权重)。
上下文感知的重排:结合用户的会话上下文(如历史提问、已查看文档),在重排时过滤重复内容、补充关联内容,例如用户先问 "Python 列表用法",再问 "排序方法",重排时优先返回与列表排序强相关的文档。
强化学习动态优化:将重排视为序列决策问题,以用户的点击、停留、反馈为奖励信号,通过强化学习训练个性化重排策略,持续优化排序效果。
典型应用
电商 RAG 客服系统中,对普通消费者重排时优先展示商品使用教程和售后政策,对商家用户则优先展示批量采购方案和 API 对接文档。
重排过程的可解释性
核心痛点
基于深度学习的重排模型是 "黑盒",用户 / 开发者无法知晓 "为什么文档 A 比文档 B 排名更高",在医疗、法律等强监管领域,缺乏可解释性会导致模型无法落地,同时也不利于问题排查和效果迭代。
核心思路
让重排模型在输出排序结果的同时,提供可解释的依据(如匹配的关键词、语义关联的句子、引用的知识),让排序逻辑透明化。
落地路径
注意力可视化:利用模型的注意力权重,标注出查询与文档中 "贡献最大" 的匹配片段(如高亮 "糖尿病" 与 "血糖控制" 的语义关联),作为排序的依据。
特征归因分析:通过 LIME、SHAP 等可解释性工具,量化每个特征(如词重叠度、语义相似度、知识一致性)对最终排序得分的贡献,生成 "得分拆解报告"。
规则与模型融合:在重排模型中嵌入可解释的规则模块(如 "包含核心实体的文档加权重""事实冲突的文档降权"),并将规则触发情况作为解释依据,兼顾模型精度与可解释性。
典型应用
法律 RAG 系统中,重排模型在返回判例文档时,同时标注 "该文档因包含与当前案件匹配的'侵权责任认定条款'(相似度 0.92)且无法律冲突,排名第 1",提升结果的可信度和合规性。
各方向的技术共性与挑战
共性:均需基于 LLM / 预训练模型的语义理解能力,同时结合外部信息(知识、模态特征、用户数据、解释性工具)拓展模型能力边界。
挑战
知识增强需解决 "知识噪声" 和 "知识更新" 问题
跨模态重排需平衡多模态编码的效率与精度
个性化重排需保护用户隐私,避免过度个性化导致信息茧房
可解释性需在 "解释粒度" 和 "模型性能" 间做权衡