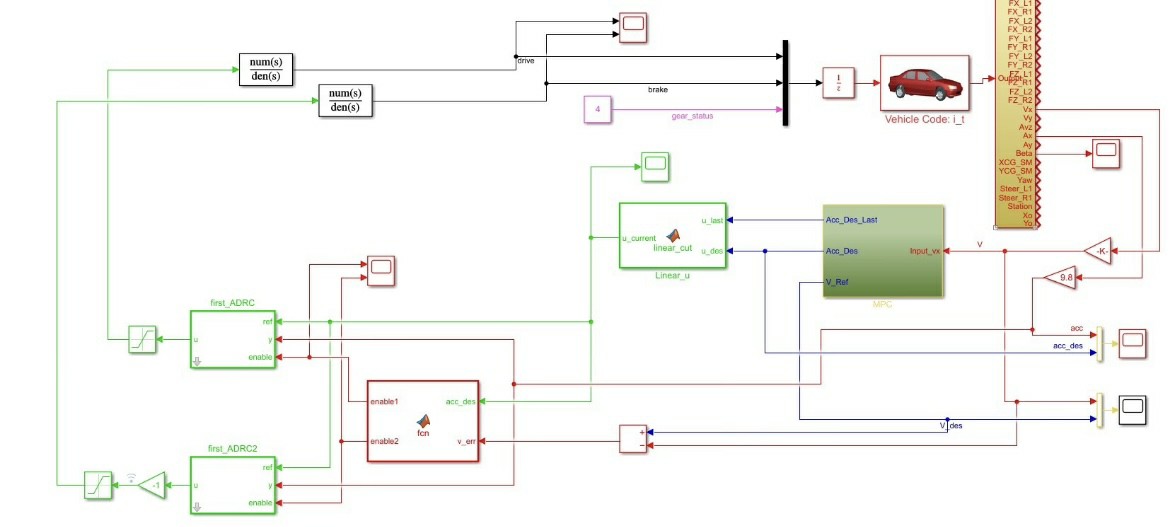
基于模型预测MPC实现的车速控制,控制目标为燃油汽车,采用上下层控制器控制,上层mpc产生期望的加速度,下层采用自抗扰ADRC控制产生期望的节气门开度和制动压力,同时该算法可直接用于代码生成(可做实车试验实验),后续可以用于车速需求的控制(如acc,轨迹跟踪等)
在汽车控制领域,实现精准的车速控制一直是研究热点。今天来聊聊基于模型预测MPC实现的燃油汽车车速控制方法,这种方法采用上下层控制器的设计思路,十分巧妙。
上下层控制器架构
上层由MPC(模型预测控制)负责产生期望的加速度。MPC的核心思想是基于系统的模型,预测系统未来的行为,并在每个采样时刻求解一个优化问题,以确定当前时刻的最优控制输入。以下是一个简单的MPC原理代码示意(这里以Python和numpy为例,实际应用会更复杂且结合车辆动力学模型):
python
import numpy as np
# 假设简单的车辆动力学模型离散化参数
A = np.array([[1, 0.1], [0, 1]])
B = np.array([[0.05], [0.1]])
Q = np.diag([1, 1])
R = np.diag([0.1])
# 预测时域
N = 5
def mpc(state, ref):
X = np.zeros((2, N + 1))
U = np.zeros((1, N))
X[:, 0] = state
for k in range(N):
cost = 0
for i in range(k, N):
cost += (X[0, i] - ref[i]) ** 2 * Q[0, 0] + X[1, i] ** 2 * Q[1, 1] + U[0, i] ** 2 * R[0, 0]
# 这里省略具体求解最优U的过程,实际可能用优化库
U[0, k] = 0.1 # 简单假设一个控制量
X[:, k + 1] = A.dot(X[:, k]) + B.dot(U[:, k])
return U[0, 0]这里代码通过定义简单的车辆动力学模型矩阵A和B,以及权重矩阵Q和R,构建了MPC基本框架。在mpc函数中,通过循环预测未来状态并计算代价函数,虽然这里简单假设了控制量的生成,实际应用中会利用优化算法精确求解最优控制输入,即期望的加速度。
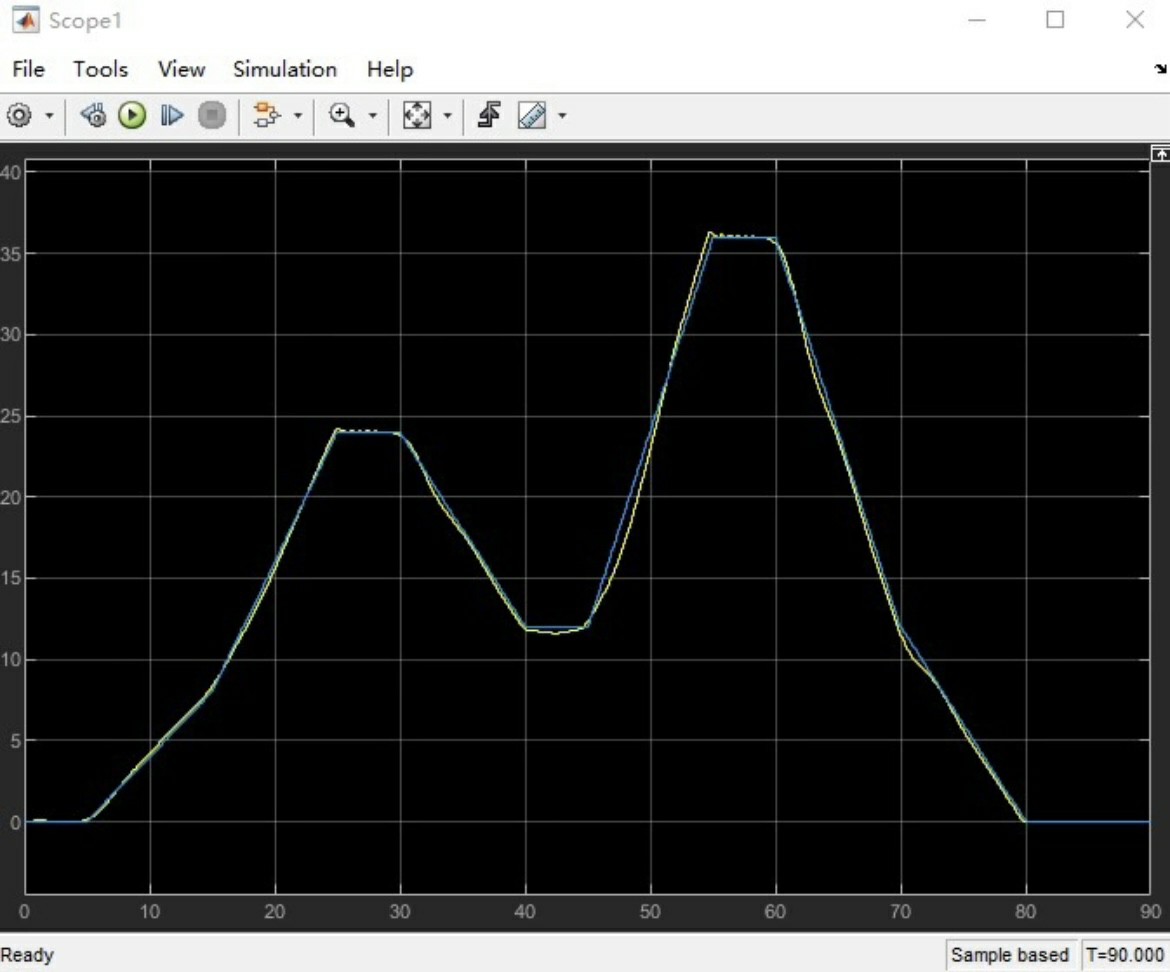
下层则采用自抗扰ADRC(Active Disturbance Rejection Control)控制来产生期望的节气门开度和制动压力。ADRC的优势在于对系统内部和外部的不确定干扰具有很强的抑制能力,能够适应燃油汽车复杂的行驶工况。ADRC的代码实现一般围绕扩张状态观测器(ESO)和非线性状态误差反馈控制律(NLSEF)展开,下面是一个简易的ADRC框架代码(以Python为例):
python
class ADRC:
def __init__(self, b0, beta01, beta02, beta03, kp, ki, kd):
self.b0 = b0
self.beta01 = beta01
self.beta02 = beta02
self.beta03 = beta03
self.kp = kp
self.ki = ki
self.kd = kd
self.x1 = 0
self.x2 = 0
self.x3 = 0
self.e1 = 0
self.e0 = 0
self.integral = 0
def fal(self, e, alpha, delta):
if abs(e) <= delta:
return e / (delta ** (1 - alpha))
else:
return np.sign(e) * (abs(e) ** alpha)
def update(self, setpoint, process_variable):
self.e1 = setpoint - process_variable
self.x1 = self.x1 + 0.01 * self.x2
self.x2 = self.x2 + 0.01 * (self.x3 + self.b0 * self.e1 - self.fal(self.x1 - process_variable, 0.5, 0.1))
self.x3 = self.x3 - 0.01 * self.fal(self.x1 - process_variable, 0.25, 0.1)
self.integral = self.integral + self.e1 * 0.01
u0 = self.kp * self.e1 + self.ki * self.integral + self.kd * (self.e1 - self.e0)
u = (u0 - self.x3) / self.b0
self.e0 = self.e1
return u在上述代码中,ADRC类通过初始化一系列参数,定义了fal函数用于计算非线性项,update函数则实现了ADRC的核心更新过程,根据设定值和当前过程变量来计算控制输出,也就是期望的节气门开度或制动压力。
代码生成与实车试验
这种基于MPC和ADRC的车速控制算法的一大亮点是可直接用于代码生成,并且能够做实车试验。通过代码生成工具,可以将上述算法转化为适用于车载控制器的代码。在实车试验中,工程师们可以收集实际行驶数据,进一步优化算法参数,确保在各种路况和驾驶场景下都能实现稳定且精准的车速控制。
未来应用拓展
后续,该算法在车速需求控制方面具有广泛的应用前景。比如自适应巡航控制(ACC),通过实时监测前车距离和本车速度,利用MPC和ADRC算法可以动态调整车速,保持安全车距。在轨迹跟踪方面,结合车辆的位置信息和预设轨迹,MPC生成期望加速度,ADRC负责精准执行,确保车辆能够准确沿着规划轨迹行驶。
总之,基于模型预测MPC实现的燃油汽车车速控制,这种上下层控制器结合的方式,为汽车控制领域带来了新的思路和解决方案,期待它在未来汽车技术发展中发挥更大作用。