2 数组 递归 复杂度 字符串

数据结构层面，大家需要掌握以下几种：

• 数组
• 栈
• 队列
• 链表
• 树（这里我们着重讲二叉树）

对于这些数据结构，各位如果没有大量的可支配时间可以投入，那么其实不建议找厚厚的大学教材来刷。此时此刻，时间为王，我们追求的是效率的最大化。

不同的数据结构教材，对数据结构有着不同的划分、不同的解读、不同的编码实现。在这里，我们面向 JavaScript，面向前端面试，只针对大家后续做题、答题时会用到的最贴合实战的数据结构特性&编码技能作讲解。

<math xmlns="http://www.w3.org/1998/Math/MathML"> 保姆式教学の 温情提示： \color{LightPink}{保姆式教学の}\color{Pink}{温情提示：} </math>保姆式教学の温情提示：

这两节我们所提及的基础知识细节，很可能会成为你后面写代码的关键线索。
不要因为乍一看觉得简单，就急着跳读急着做题 。

不然你很可能做题做到一半，会不知道自己到底为什么就卡了壳。

到时候万一又因为懒得回头看，而原地卡死，那就更做不下去了orz。

注：由于 JavaScript 中字符串和数组关联紧密，关键知识点重复度较高，故我们在数据结构部分，不再单独为字符串保留篇幅。字符串相关的知识点，我们直接带到后续的解题技巧归纳专题里去看。

数组

数组是各位要认识的第一个数据结构。

作为最简单、最基础的数据结构，大多数的语言都天然地对数组有着原生的表达，JavaScript 亦然。这意味着我们可以对数组做到"开箱即用"，而不必自行模拟实现，非常方便。

考虑到日常开发过程中，数组的出镜率本身已经很高，相信它也是大多数同学最熟悉的数据结构。 即便如此，这里仍然需要提醒各位：要对数组格外走点心，毕竟后面需要它帮忙的地方会非常多。

数组的创建

大家平时用的最多的创建方式想必就是直接方括号+元素内容这种形式：

const arr = [1, 2, 3, 4]   

不过在算法题中，很多时候我们初始化一个数组时，并不知道它内部元素的情况。这种场景下，要给大家推荐的是构造函数创建数组的方法：

const arr = new Array()

当我们以构造函数的形式创建数组时，若我们像楼上这样，不传任何参数，得到的就会是一个空数组。等价于：

const arr = []

不过咱们使用构造函数，可不是为了创建空数组这么无聊。

我们需要它的时候，往往是因为我们有"创造指定长度的空数组"这样的需求。需要多长的数组，就给它传多大的参数：

const arr = new Array(7)

这样的写法就可以得到一个长度为7的数组：

在一些场景中，这个需求会稍微变得有点复杂------ "创建一个长度确定、同时每一个元素的值也都确定的数组"。这时我们可以调用 fill 方法，假设需求是每个坑里都填上一个1，只需给它 fill 一个1：

const arr = (new Array(7)).fill(1)

如此便可以得到一个长度为7，且每个元素都初始化为1的数组：

数组的访问和遍历

访问数组中的元素，我们直接在中括号中指定其索引即可：

arr[0] // 访问索引下标为0的元素

而遍历数组，这个方法就多了，不过目的往往都是一致的------访问到数组中的每个元素，并且知道当前元素的索引。这里我们讲三个方法：

1. for 循环
   这个是最最基础的操作。我们可以通过循环数组的下标，来依次访问每个值：

// 获取数组的长度
const len = arr.length
for(let i=0;i<len;i++) {
    // 输出数组的元素值，输出当前索引
    console.log(arr[i], i)
}

2. forEach 方法
   通过取 forEach 方法中传入函数的第一个入参和第二个入参，我们也可以取到数组每个元素的值及其对应索引：

arr.forEach((item, index)=> {
    // 输出数组的元素值，输出当前索引
    console.log(item, index)
})

3. map 方法
   map 方法在调用形式上与 forEach 无异，区别在于 map 方法会根据你传入的函数逻辑对数组中每个元素进行处理、进而返回一个全新的数组。
   所以其实 map 做的事情不仅仅是遍历，而是在遍历的基础上"再加工"。当我们需要对数组内容做批量修改、同时修改的逻辑又高度一致时，就可以调用 map 来达到我们的目的：

const newArr = arr.map((item, index)=> {
    // 输出数组的元素值，输出当前索引
    console.log(item, index)
    // 在当前元素值的基础上加1
    return item+1
})

这段代码就通过 map 来返回了一个全新的数组，数组中每个元素的值都是在其现有元素值的基础上+1后的结果。

这里给个小建议：个人推荐如果没有特殊的需要，那么统一使用 for 循环来实现遍历。因为从性能上看，for 循环遍历起来是最快的。

二维数组

初学编程的同学基础如果比较薄弱，会对二维数组完全没有概念。这里咱们先简单介绍下：二维数组其实就是数组套数组，也就是每个元素都是数组的数组。

说起来有点绕口，咱们直接上图来看：

const arr = [1,2,3,4,5]

这个数组在逻辑上的分布就是这样式儿的：

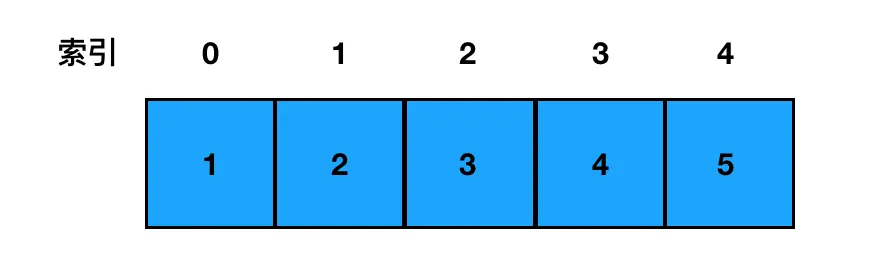
像图上这样，数组的元素是数字而非数组。整个数组的结构看上去宛如一条"线"，这就是一维数组。

而"每个元素都是数组的数组"，代码里看是这样：

const arr = [
  [1,2,3,4,5],
  [1,2,3,4,5],
  [1,2,3,4,5],
  [1,2,3,4,5],
  [1,2,3,4,5]
]

直接把它的逻辑结构画出来看，是这样：

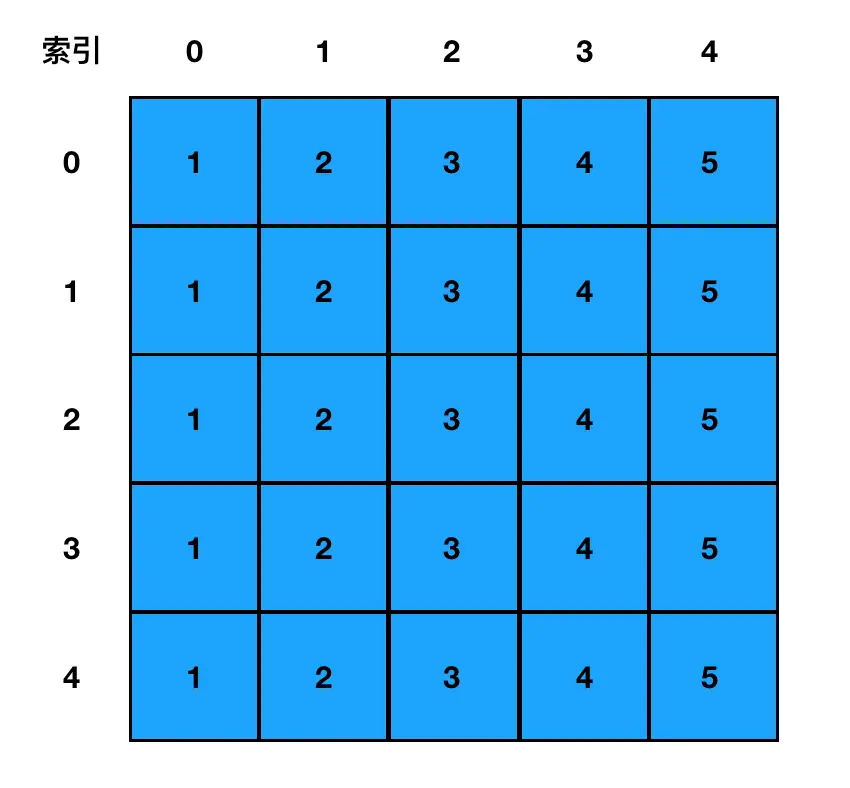
图中的每一行，就代表着一个数组元素。比如第 0 行，就代表着数组中 arr[0] 这个数组元素，其内容是 [1,2,3,4,5]。

每一行中的每一列，则代表一个确切的"坑"。比如第 0 行第 1 列，就代表着数组中 arr[0][1] 这个元素，其值为2，是一个确切的 number。

明白了二维数组的索引规律，现在我们来看一下二维数组的特点：从形状上看，相对于一维数组一条"线"一般的布局，二维数组更像是一个"面"。拿咱们这个例子来说，这里的二维数组逻辑分布图就宛如一个正方形。当然啦，如果我们稍微延长一下其中的一边，它也可以是一个矩形。

在数学中，形如这样长方阵列排列的复数或实数集合 ，被称为"矩阵"。因此二维数组的别名就叫"矩阵"。

讲到这里，如果有对"矩阵"的定义一脸懵逼的同学，也不用怕------不知道"矩阵"是啥，一点不打紧（所以快停下你复制粘贴到 Google 的手哈哈），但你必须要记住"矩阵"和"二维数组"之间的等价关系。在算法题目中，见到"矩阵"时，能够立刻反射出它说的是二维数组，不被别名整懵逼，这就够了。

二维数组的初始化

fill 的局限性

有同学用 fill 方法用顺了手，就本能地想用 fill 解决所有的问题，比如初始化一个二维数组：

const arr =(new Array(7)).fill([])

乍一看没啥毛病，7个坑都被乖乖地填上了数组元素：

但是当你想修改某一个坑里的数组的值的时候：

arr[0][0] = 1

你会发现一整列的元素都被设为了 1：

这是什么骚操作？？？

这就要从 fill 的工作机制讲起了。各位要清楚，当你给 fill 传递一个入参时，如果这个入参的类型是引用类型，那么 fill 在填充坑位时填充的其实就是入参的引用 。也就是说下图中虽然看似我们给7个坑位各初始化了一个数组：

其实这7个数组对应了同一个引用、指向的是同一块内存空间，它们本质上是同一个数组。因此当你修改第0行第0个元素的值时，第1-6行的第0个元素的值也都会跟着发生改变。

初始化一个二维数组

本着安全的原则，这里我推荐大家采纳的二维数组初始化方法非常简单（而且性能也不错）。直接用一个 for 循环来解决：

const len = arr.length
for(let i=0;i<len;i++) {
    // 将数组的每一个坑位初始化为数组
    arr[i] = []
}

for 循环中，每一次迭代我们都通过"[]"来创建一个新的数组，这样便不会有引用指向问题带来的尴尬。

二维数组的访问

访问二维数组和访问一维数组差别不大，区别在于我们现在需要的是两层循环：

// 缓存外部数组的长度
const outerLen = arr.length
for(let i=0;i<outerLen;i++) {
    // 缓存内部数组的长度
    const innerLen = arr[i].length
    for(let j=0;j<innerLen;j++) {
        // 输出数组的值，输出数组的索引
        console.log(arr[i][j],i,j)
    }
}

一维数组用 for 循环遍历只需一层循环，二维数组是两层，三维数组就是三层。依次类推，N 维数组需要 N 层循环来完成遍历。

数组小结

关于数组的基础知识，咱们整整用掉了一节的篇幅来介绍，可见其重要性。

在本节，我们仅仅围绕数组最基本的操作进行介绍，这远不是数组的全部。关于数组，还有太多太多的故事要讲------实际上，单就其重要的方法的使用：如concat、some、slice、join、sort、pop、push 等等这些，就足以说上个把钟头。

本节暂时不对数组 API 作集中讲解，因为罗列 API 没有意义------脱离场景去记忆 API 实在是一件太痛苦的事情，这会挫伤各位继续走下去的积极性。

关于数组的更多特性和技巧，会被打散到后续的章节中去。各位在真题解读的环节、包括在其它数据结构的讲解中，都会不可避免地再见到数组的身影。彼时数组的每一个方法都会和它对应的应用场景一起出现，相信你会有更深刻的记忆。

事实上，在 JavaScript 数据结构中，数组几乎是"基石"一般的存在。这一点，大家在下一节就会有所感触。

（阅读过程中有任何想法或疑问，或者单纯希望和笔者交个朋友啥的，欢迎大家添加我的微信xyalinode与我交流哈~）

本节我们基于对数组的理解和掌握，围剿线性数据结构（栈、队列和链表）。

栈和队列

在 JavaScript 中，栈和队列的实现一般都要依赖于数组，大家完全可以把栈和队列都看作是"特别的数组"。

（注：实际上，栈和队列作为两种运算受限的线性表，用链表来实现也是没问题的。只是从前端面试做题的角度来说，基于链表来实现栈和队列约等于脱裤子放屁（链表实现起来会比数组麻烦得多，做不到开箱即用），基本没人会这么干。这里大家按照数组的思路往下走就行了）

两者的区别在于，它们各自对数组的增删操作有着不一样的限制。因此，在学习栈与队列之前，我们需要先来明确一下数组中的增删操作具有什么样的特性、对应的方法有哪些：

灵活增删的数组

数组的增删操作可以说是没有任何限制的，允许我们在任何位置执行想要的操作。

数组中增加元素的三种方法

• unshift 方法-添加元素到数组的头部

const arr = [1,2]
arr.unshift(0) // [0,1,2]

• push 方法-添加元素到数组的尾部

const arr = [1,2]
arr.push(3) // [1,2,3]

• splice 方法-添加元素到数组的任何位置

const arr = [1,2] 
arr.splice(1,0,3) // [1,3,2]

这里重点讲一下这个 splice 方法。很多同学对传入两个以上的参数这种用法可能比较陌生。大家相对熟悉的应该还是 splice 用于删除的操作：

arr.splice(1,1)

第一个入参是起始的索引值，第二个入参表示从起始索引开始需要删除的元素个数。这里我们指明从索引为1的元素开始，删掉1个元素，也就相当于把 arr[1] 给删掉了。这就是数组中删除任意位置元素的方法 。

至于传入两个以上参数这种用法，是用于在删除的同时完成数组元素的新增。而从第三个位置开始的入参，都代表着需要添加到数组里的元素的值：

arr.splice(1,0,3) // [1,3,2]

在这个例子里，我们就指明了从 arr[1] 开始，删掉 0 个元素，并且在索引为1的地方新增了值为3的元素。

因为删掉的元素是0个，所以说 arr[1] 中原有的元素值"2"仍然会被保留下来；同时因为我们后面又指定了 arr[1] 处需要新增一个元素3，那么这个3就会把原来arr[1]这个地方的元素给"挤到后面去"。这样我们就做到了在数组中任意位置进行元素的新增。这个过程如下图：

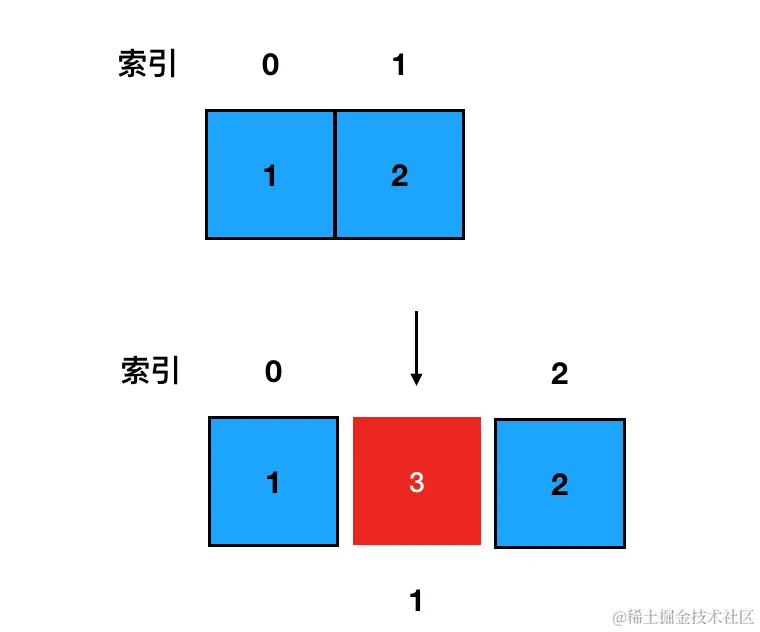
数组中删除元素的三种方法

• shift 方法-删除数组头部的元素

const arr = [1,2,3]
arr.shift() // [2,3]

• pop 方法-删除数组尾部的元素

const arr = [1,2,3]
arr.pop() // [1,2]

• splice 方法-删除数组任意位置的元素
  splice 方法我们上文已经详细讲过，此处不再赘述。

栈（Stack）------只用 pop 和 push 完成增删的"数组"

栈是一种后进先出(LIFO，Last In First Out)的数据结构。

我们可以把它想象成小时候学校门口小卖部里，摞满了冰淇淋的方形大冰柜。

小卖部老板往里面摆置冰淇淋的时候，最先摆进去的会落在冰柜的底部，最后摆置进去的留在冰柜的顶部。如果这时候咱们去买冰淇淋，老板就会把冰柜顶部的那个取出来给我们。在冰淇淋不断被取出的这个过程里，越是后来放进去的，越是先被取出来；越是先放进去的，越是最后被取出来。这个过程，就是所谓的"后进先出"：

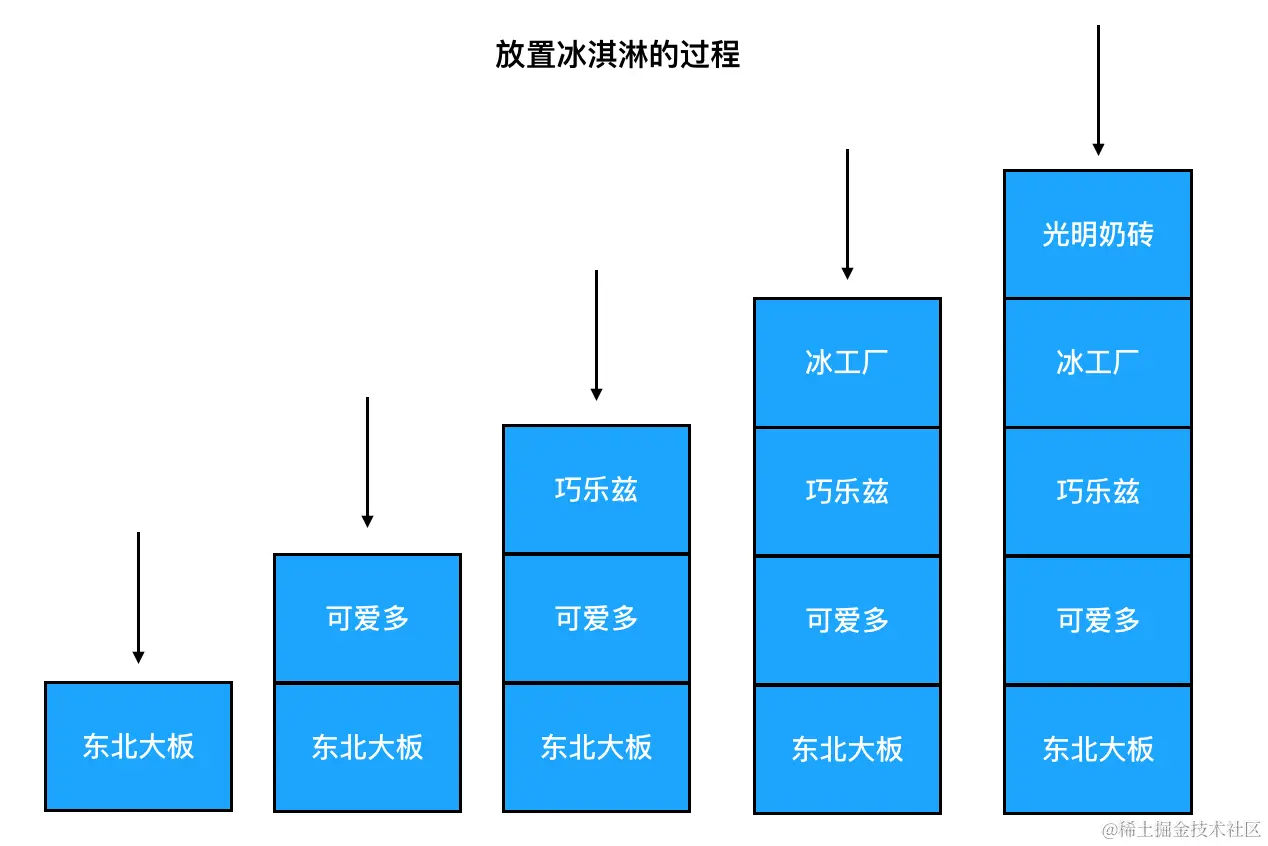
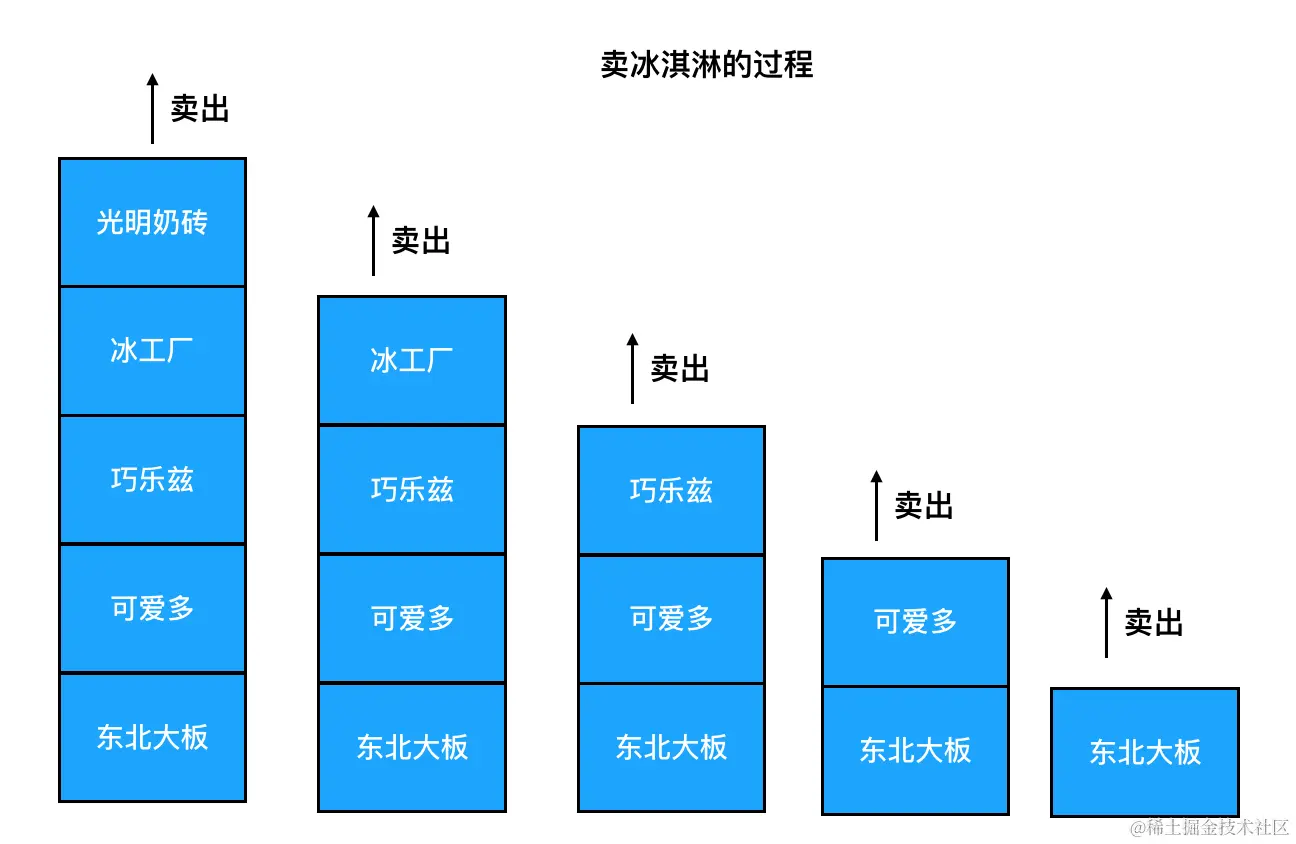
我们看到这个过程有两个特征：

• 只允许从尾部添加元素
• 只允许从尾部取出元素
  对应到数组的方法，刚好就是 push 和 pop。因此，我们可以认为在 JavaScript 中，栈就是限制只能用 push 来添加元素，同时只能用 pop 来移除元素的一种特殊的数组。

除了 pop 和 push 之外，栈相关的面试题中往往还会涉及到取栈顶元素的操作。所谓栈顶元素，从图上我们不难看出来，实际上它指的就是数组尾部的元素。

下面我们基于数组来实现一波栈的常用操作，完成"放置冰淇淋"和"卖冰淇淋"的过程：

// 初始状态，栈空
const stack = []  
// 入栈过程
stack.push('东北大板')
stack.push('可爱多')
stack.push('巧乐兹')
stack.push('冰工厂')
stack.push('光明奶砖')

// 出栈过程，栈不为空时才执行
while(stack.length) {
    // 单纯访问栈顶元素（不出栈）
    const top = stack[stack.length-1]
    console.log('现在取出的冰淇淋是', top)  
    // 将栈顶元素出栈
    stack.pop()
}

// 栈空
stack // []

丢到控制台运行，冰淇淋就会按照后进先出的顺序被取出：

队列（Queue）------只用 push 和 shift 完成增删的"数组"

队列是一种先进先出（FIFO，First In First Out）的数据结构。

它比较像咱们去肯德基排队点餐。先点餐的人先出餐，后点餐的人后出餐：

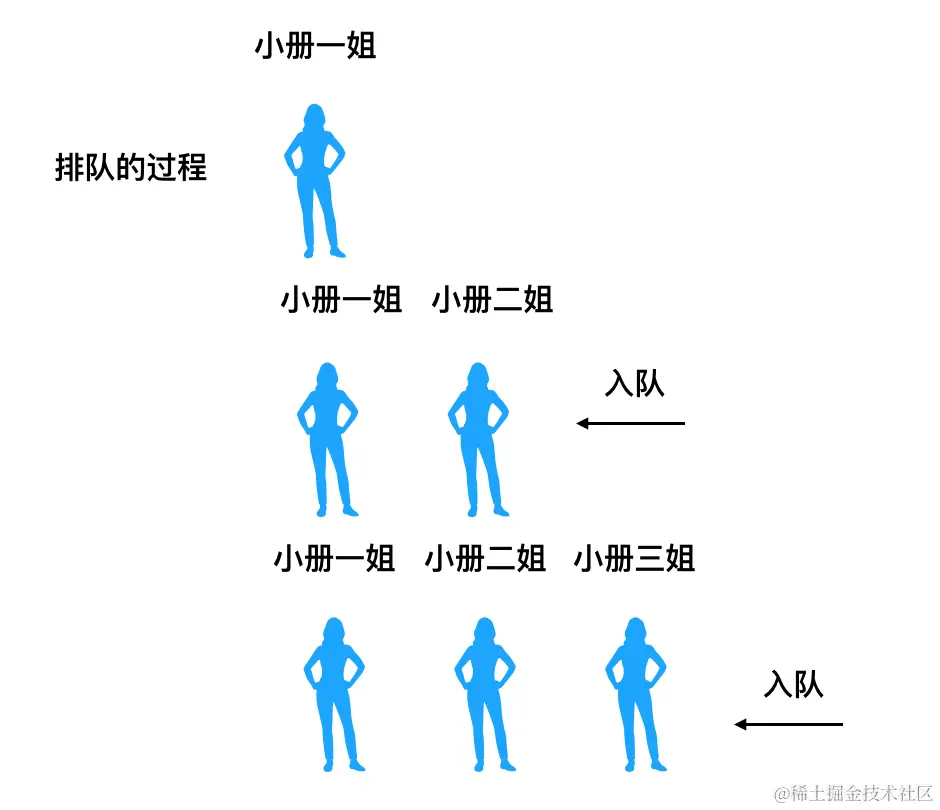
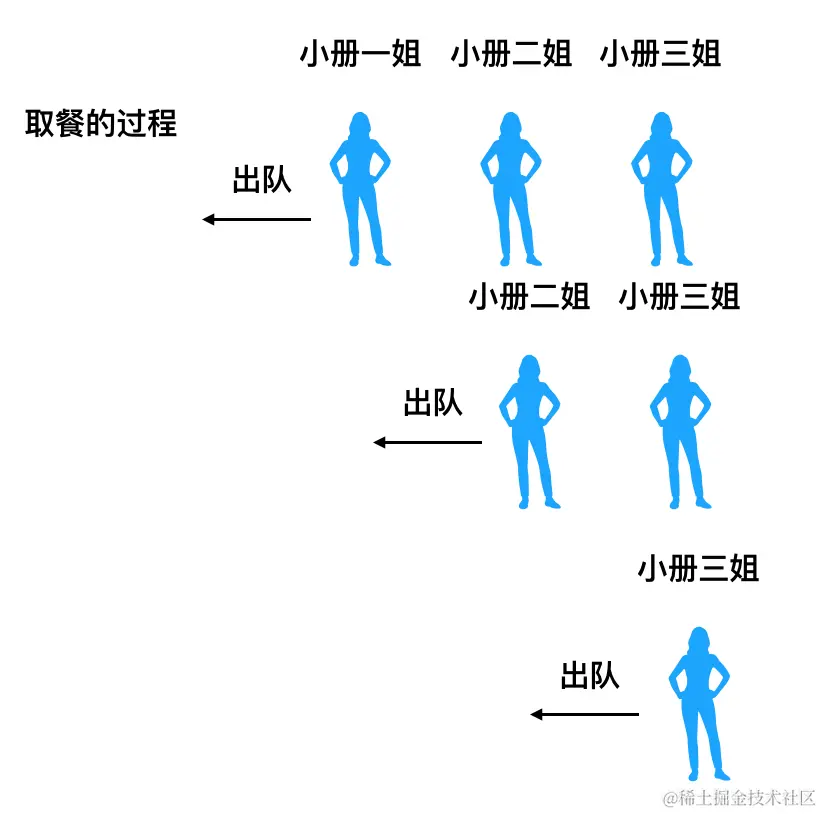
这个过程的规律也很明显：

• 只允许从尾部添加元素
• 只允许从头部移除元素

也就是说整个过程只涉及了数组的 push 和 shift 方法。

在栈元素出栈时，我们关心的是栈顶元素（数组的最后一个元素）；队列元素出队时，我们关心的则是队头元素（数组的第一个元素）。

下面我们基于数组来实现一波队列的常用操作，完成"小册姐排队"和"小册姐取餐"的过程：

const queue = []  
queue.push('小册一姐')
queue.push('小册二姐')
queue.push('小册三姐')  
  
while(queue.length) {
    // 单纯访问队头元素（不出队）
    const top = queue[0]
    console.log(top,'取餐')
    // 将队头元素出队
    queue.shift()
}

// 队空
queue // []

把上面代码丢进控制台运行，我们可以看到小册姐一个接一个地乖乖去取餐了：

链表

链表和数组相似，它们都是有序的列表、都是线性结构（有且仅有一个前驱、有且仅有一个后继）。不同点在于，链表中，数据单位的名称叫做"结点"，而结点和结点的分布，在内存中可以是离散的。

这个"离散"是相对于数组的"连续"来说的。上一节咱们给大家画过数组的元素分布示意图：

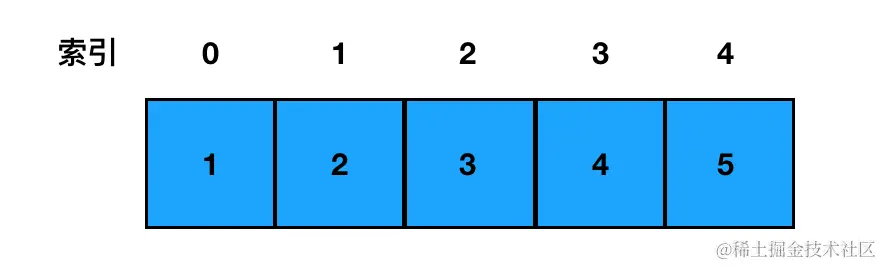
数组在内存中最为关键的一个特征，就是它一般是对应一段位于自己上界和下界之间的、一段连续的内存空间。元素与元素之间，紧紧相连（当然啦，还有二般情况，我们在下文的辨析环节会提到）。

而链表中的结点，则允许散落在内存空间的各个角落里。一个内容为1->2->3->4->5的链表，在内存中的形态可以是散乱如下的：

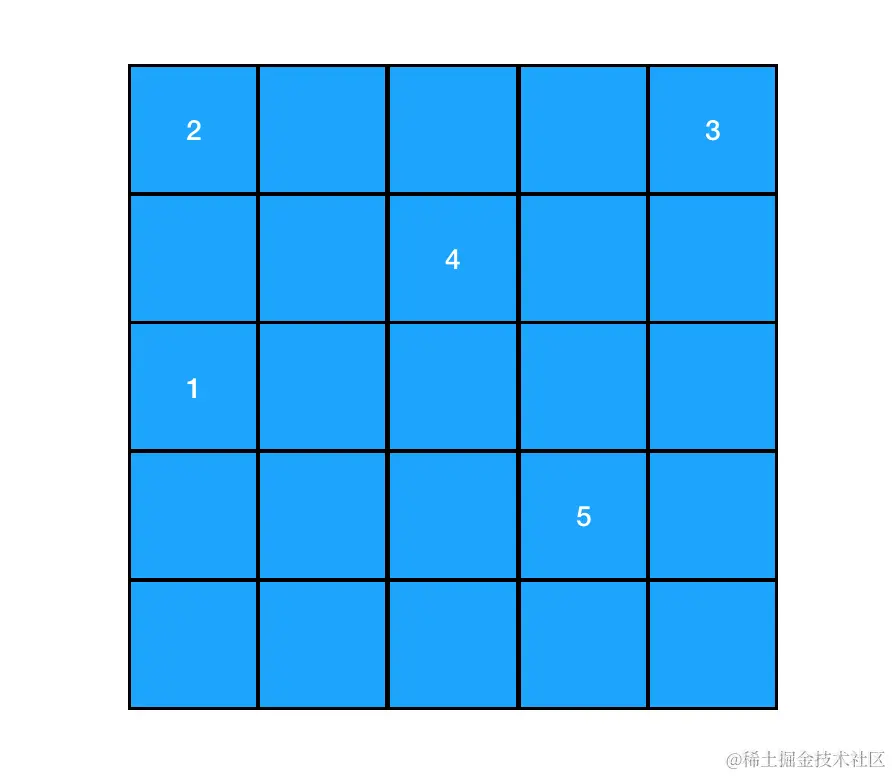
正是由于数组中的元素是连续的，每个元素的内存地址可以根据其索引距离数组头部的距离来计算出来。因此对数组来说，每一个元素都可以通过数组的索引下标直接定位。

但是对链表来说，元素和元素之间似乎毫无内存上的瓜葛可言。就比如说咱们图上这种情况，1、2、3、4、5各据山头，站在元素1的坑位里，我们对元素2、3、4、5的内存地址一无所知，连遍历都没法遍历，这可咋整？

没有关联，就创造关联！

在链表中，每一个结点的结构都包括了两部分的内容：数据域和指针域。JS 中的链表，是以嵌套的对象的形式来实现的：

{
    // 数据域
    val: 1,
    // 指针域，指向下一个结点
    next: {
        val:2,
        next: ...
    }
}   

数据域存储的是当前结点所存储的数据值，而指针域则代表下一个结点（后继结点）的引用。 有了 next 指针来记录后继结点的引用，每一个结点至少都能知道自己后面的同学是哪位了，原本相互独立的结点之间就有了如下的联系：

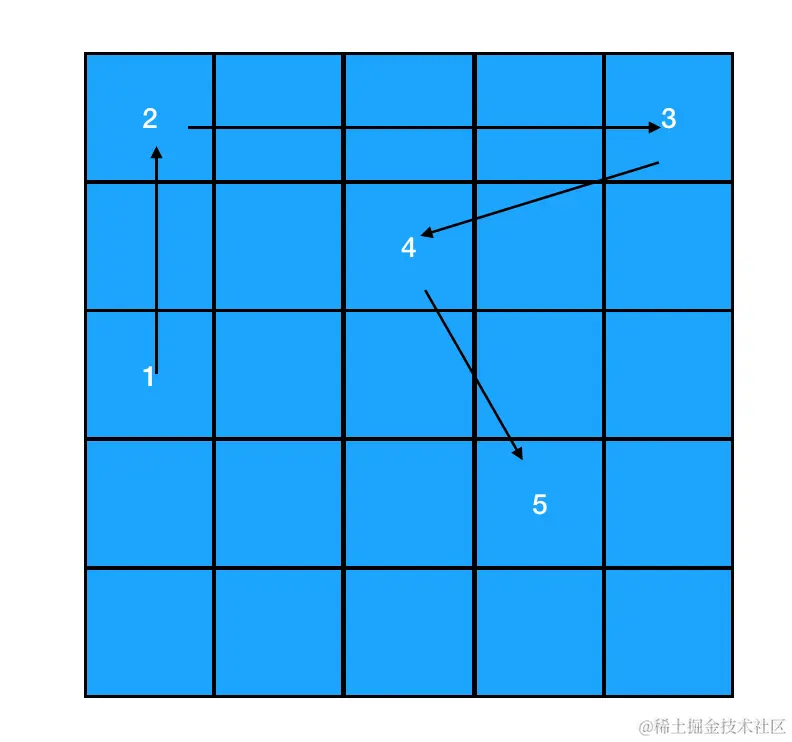
我们把这个关系给简化一下：

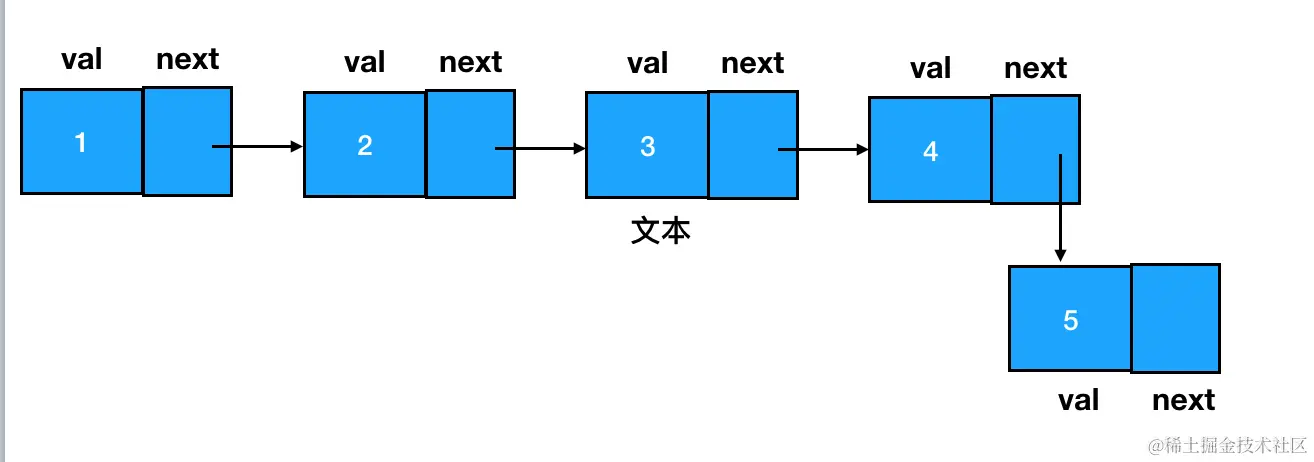
要想访问链表中的任何一个元素，我们都得从起点结点开始，逐个访问 next，一直访问到目标结点为止。为了确保起点结点是可抵达的，我们有时还会设定一个 head 指针来专门指向链表的开始位置：

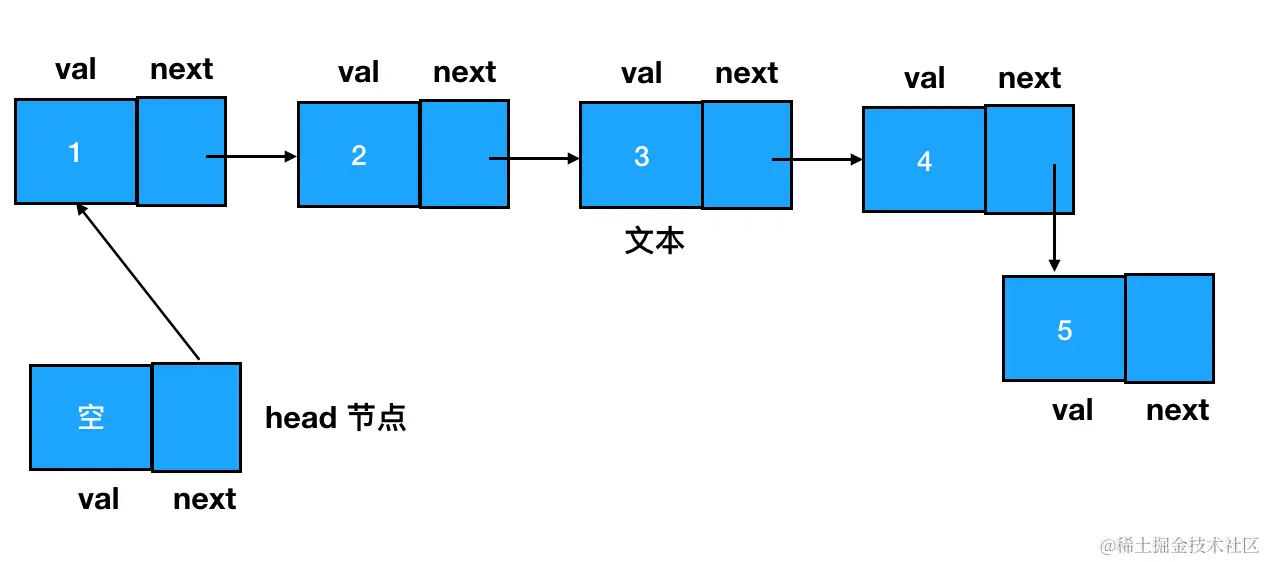
以上，就是链表的基本形态啦。

链表结点的创建

创建链表结点，咱们需要一个构造函数：

function ListNode(val) {
    this.val = val;
    this.next = null;
}

在使用构造函数创建结点时，传入 val （数据域对应的值内容）、指定 next （下一个链表结点）即可：

const node = new ListNode(1)  
node.next = new ListNode(2)

以上，就创建出了一个数据域值为1，next 结点数据域值为2的链表结点：

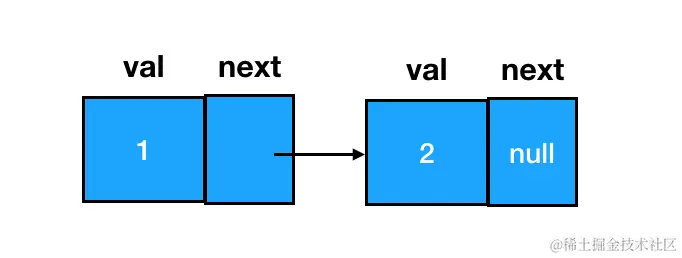
链表元素的添加

结合前面的学习，我们已经知道，链表的结点间关系是通过 next 指针来维系的。因此，链表元素的添加和删除操作，本质上都是在围绕 next 指针做文章。

先来说说添加，直接在尾部添加结点相对比较简单，我们改变一个 next 指针就行。这里记值为2的 node 结点为 node2（假设 node2 是现在的尾部结点），值为3的 node 结点为 node3。假如我要把 node3 添加到 node2 所在链表的尾部，直接把 node2 的 next 指针指向 node3 即可：

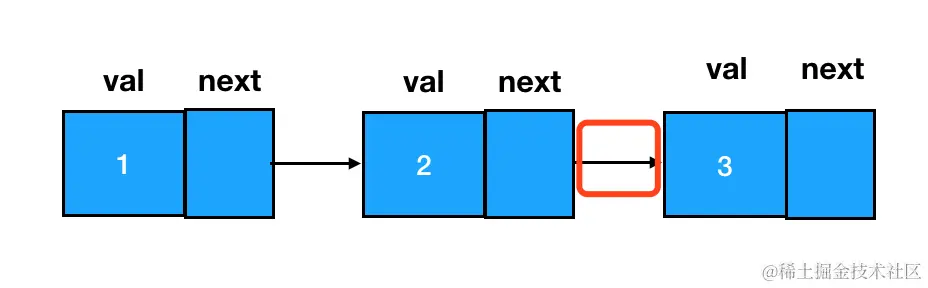
需要大家引起重视的是另一种添加操作：如何在两个结点间插入一个结点？注意，由于链表有时会有头结点，这时即便你是往链表头部增加结点，其本质也是"在头结点和第一个结点之间插入一个新结点"。所以说，任意两结点间插入一个新结点这种类型的增加操作，将会是链表基础中的一个关键考点。

要想完成这个动作，我们需要变更的是前驱结点 和目标结点 的 next 指针指向，过程如下图：

插入前：

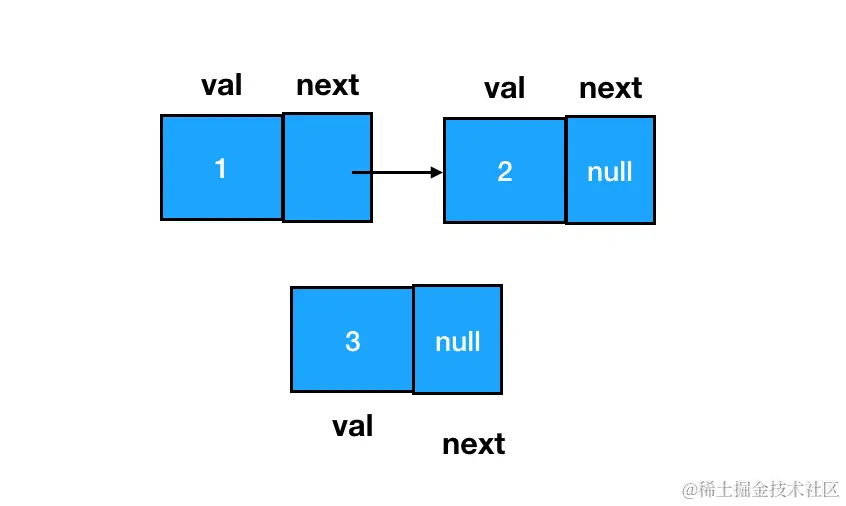插入后：

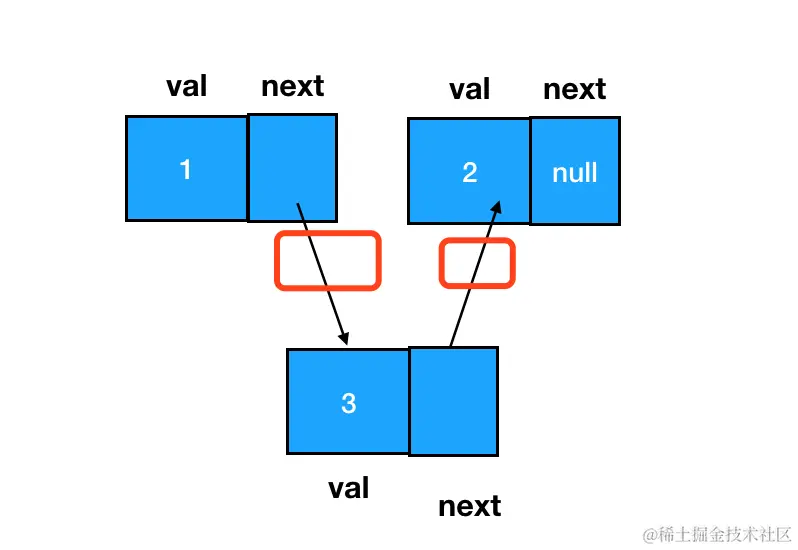
注意我圈红的地方，就是咱们要动手脚的地方。下面我用代码来表述一下这个改变。：

// 如果目标结点本来不存在，那么记得手动创建
const node3 = new ListNode(3)     
// 把node3的 next 指针指向 node2（即 node1.next）
node3.next = node1.next
// 把node1的 next 指针指向 node3
node1.next = node3

链表元素的删除

链表元素的删除也是非常高频的操作。延续我们前面的思路，仍然把重心放在对 next 指针的调整上。我们思考一下：如何把刚刚添加进来的 node3 从现在的链表里删掉？

注意，删除的标准是：在链表的遍历过程中，无法再遍历到某个结点的存在。按照这个标准，要想遍历不到 node3，我们直接让它的前驱结点 node1 的 next 指针跳过它、指向 node3 的后继即可：

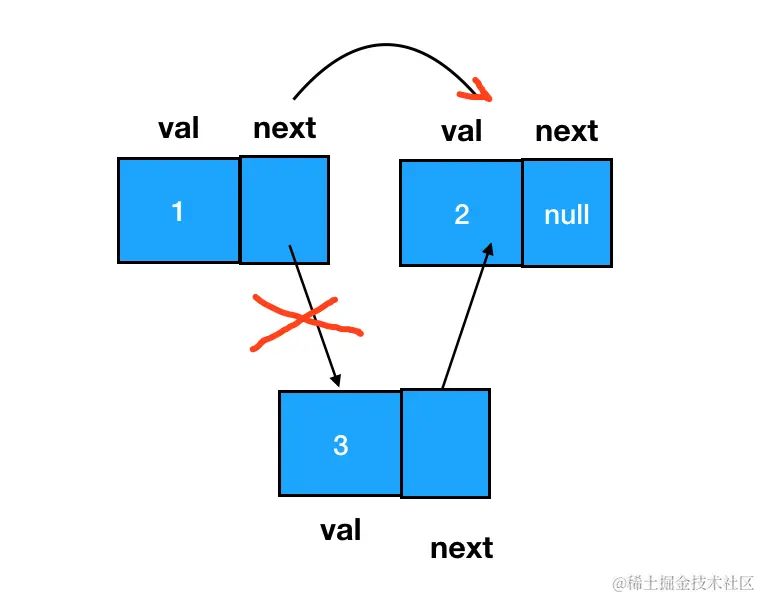
如此一来，node3 就成为了一个完全不可抵达的结点了，它会被 JS 的垃圾回收器自动回收掉。这个过程用代码表述如下：

node1.next = node3.next 

这里给大家提个醒：在涉及链表删除操作的题目中，重点不是定位目标结点，而是定位目标结点的前驱结点。做题时，完全可以只使用一个指针（引用），这个指针用来定位目标结点的前驱结点。比如说咱们这个题里，其实只要能拿到 node1 就行了：

// 利用 node1 可以定位到 node3
const target = node1.next  
node1.next = target.next

因此大家做题的时候，千万别跑过了头，最后找到了目标结点、回头却发现忘了记录真正重要的前驱结点。（这点我们后面做题的时候会再给大家提点一下）

链表和数组的辨析

在大多数的计算机语言中，数组都对应着一段连续的内存。如果我们想要在任意位置删除一个元素，那么该位置往后的所有元素，都需要往前挪一个位置；相应地，如果要在任意位置新增一个元素，那么该位置往后的所有元素也都要往后挪一个位置。
我们假设数组的长度是 n，那么因增加/删除操作导致需要移动的元素数量，就会随着数组长度 n 的增大而增大，呈一个线性关系。所以说数组增加/删除操作对应的复杂度就是 O(n)。

（关于时间复杂度，在第6小节我们会作专题讲解，大家莫慌）

但 JS 中不一定是。

JS比较特别。如果我们在一个数组中只定义了一种类型的元素，比如：

const arr = [1,2,3,4]

它是一个纯数字数组，那么对应的确实是连续内存。

但如果我们定义了不同类型的元素：

const arr = ['haha', 1, {a:1}]

它对应的就是一段非连续的内存。此时，JS 数组不再具有数组的特征，其底层使用哈希映射分配内存空间，是由对象链表来实现的。

说起来有点绕口，但大家谨记"JS 数组未必是真正的数组"即可。

何谓"真正的数组"？在各大教材（包括百科词条）对数组的定义中，都有一个"存储在连续的内存空间里"这样的必要条件。因此在本文中，我们描述的"数组"就是符合这个定义的数组。面试时，若考到数组和链表的辨析，大家也沿着这个思路往下说，是没有问题的。如果能够说出 JS 数组和常规数组的不同，那就是锦上添花了。

相对于数组来说，链表有一个明显的优点，就是添加和删除元素都不需要挪动多余的元素。

高效的增删操作

在链表中，添加和删除操作的复杂度是固定的------不管链表里面的结点个数 n 有多大，只要我们明确了要插入/删除的目标位置，那么我们需要做的都仅仅是改变目标结点及其前驱/后继结点的指针指向。 因此我们说链表增删操作的复杂度是常数级别的复杂度，用大 O 表示法表示为 O(1)。

麻烦的访问操作

但是链表也有一个弊端：当我们试图读取某一个特定的链表结点时，必须遍历整个链表来查找它。比如说我要在一个长度为 n（n>10） 的链表里，定位它的第 10 个结点，我需要这样做：

// 记录目标结点的位置
const index = 10  
// 设一个游标指向链表第一个结点，从第一个结点开始遍历
let node = head  
// 反复遍历到第10个结点为止
for(let i=0;i<index&&node;i++) {
    node = node.next
}

随着链表长度的增加，我们搜索的范围也会变大、遍历其中任意元素的时间成本自然随之提高。这个变化的趋势呈线性规律，用大 O 表示法表示为 O(n)。

但在数组中，我们直接访问索引、可以做到一步到位，这个操作的复杂度会被降级为常数级别(O(1))：

arr[9]

小结

结合上述分析，我们不难得出这样的结论：链表的插入/删除效率较高，而访问效率较低；数组的访问效率较高，而插入效率较低。这个特性需要大家牢记，可能会作为数据结构选型的依据来单独考察。

（阅读过程中有任何想法或疑问，或者单纯希望和笔者交个朋友啥的，欢迎大家添加我的微信xyalinode与我交流哈~）

快速上手------从0到1掌握算法面试需要的数据结构（三）

本节我们一起来认识一下树与二叉树。

理解树结构

在理解计算机世界的树结构之前，大家不妨回忆一下现实世界中的树有什么特点：一棵树往往只有一个树根，向上生长后，却可以伸展出无数的树枝、树枝上会长出树叶。由树根从泥土中吸收水、无机盐等营养物质，源源不断地输送到树枝与树叶的那一端。一棵树往往呈现这样的基本形态：

数据结构中的树，首先是对现实世界中树的一层简化：把树根抽象为"根结点"，树枝抽象为"边"，树枝的两个端点抽象为"结点"，树叶抽象为"叶子结点"。抽象后的树结构如下：

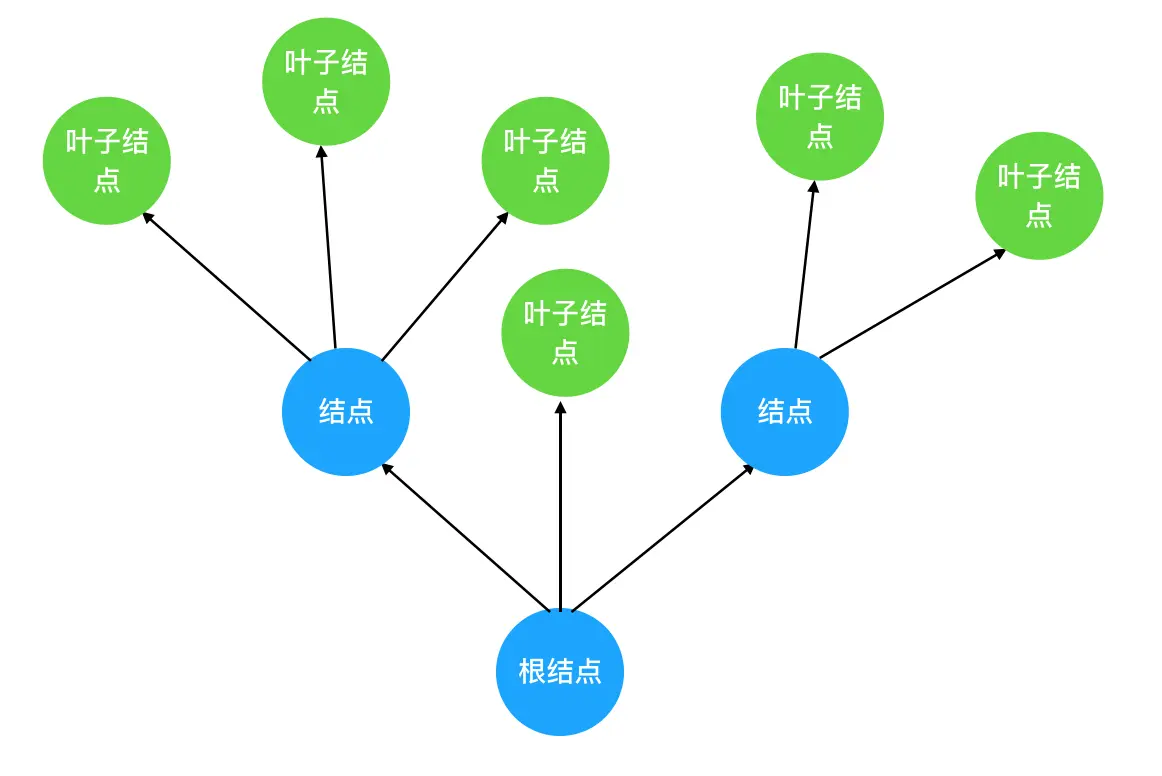
把这棵抽象后的树颠倒一下，就得到了计算机中的树结构：

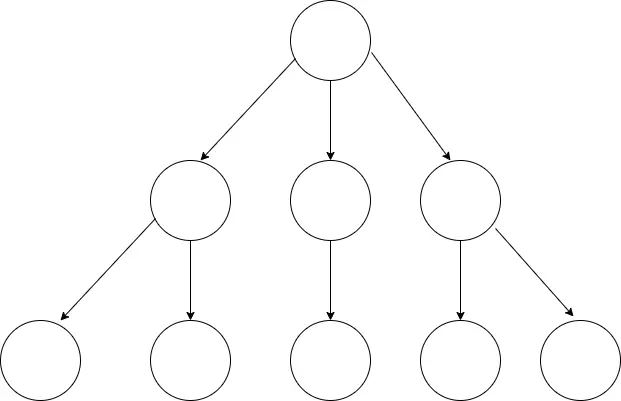
结合这张图，我们来讲解树的关键特性和重点概念。希望大家可以牢记以下几点：

• 树的层次计算规则：根结点所在的那一层记为第一层，其子结点所在的就是第二层，以此类推。
• 结点和树的"高度"计算规则：叶子结点高度记为1，每向上一层高度就加1，逐层向上累加至目标结点时，所得到的的值就是目标结点的高度。树中结点的最大高度，称为"树的高度"。
• "度"的概念：一个结点开叉出去多少个子树，被记为结点的"度"。比如我们上图中，根结点的"度"就是3。
• "叶子结点"：叶子结点就是度为0的结点。在上图中，最后一层的结点的度全部为0，所以这一层的结点都是叶子结点。

理解二叉树结构

二叉树是指满足以下要求的树：

• 它可以没有根结点，作为一棵空树存在
• 如果它不是空树，那么必须由根结点、左子树和右子树组成，且左右子树都是二叉树 。如下图：
  
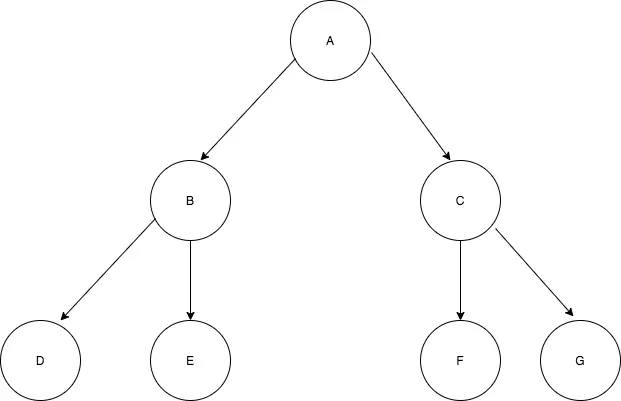
  注意，二叉树不能被简单定义为每个结点的度都是2的树。普通的树并不会区分左子树和右子树，但在二叉树中，左右子树的位置是严格约定、不能交换的。对应到图上来看，也就意味着 B 和 C、D 和 E、F 和 G 是不能互换的。

二叉树的编码实现

在 JS 中，二叉树使用对象来定义。它的结构分为三块：

• 数据域
• 左侧子结点（左子树根结点）的引用
• 右侧子结点（右子树根结点）的引用

在定义二叉树构造函数时，我们需要把左侧子结点和右侧子结点都预置为空：

// 二叉树结点的构造函数
function TreeNode(val) {
    this.val = val;
    this.left = this.right = null;
}

当你需要新建一个二叉树结点时，直接调用构造函数、传入数据域的值就行了：

const node  = new TreeNode(1)

如此便能得到一个值为 1 的二叉树结点，从结构上来说，它长这样：

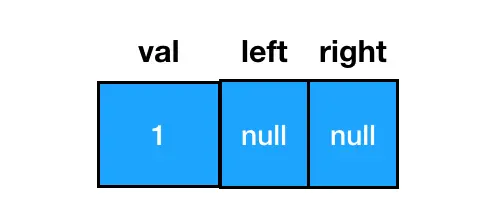
以这个结点为根结点，我们可以通过给 left/right 赋值拓展其子树信息，延展出一棵二叉树。因此从更加细化的角度来看，一棵二叉树的形态实际是这样的：

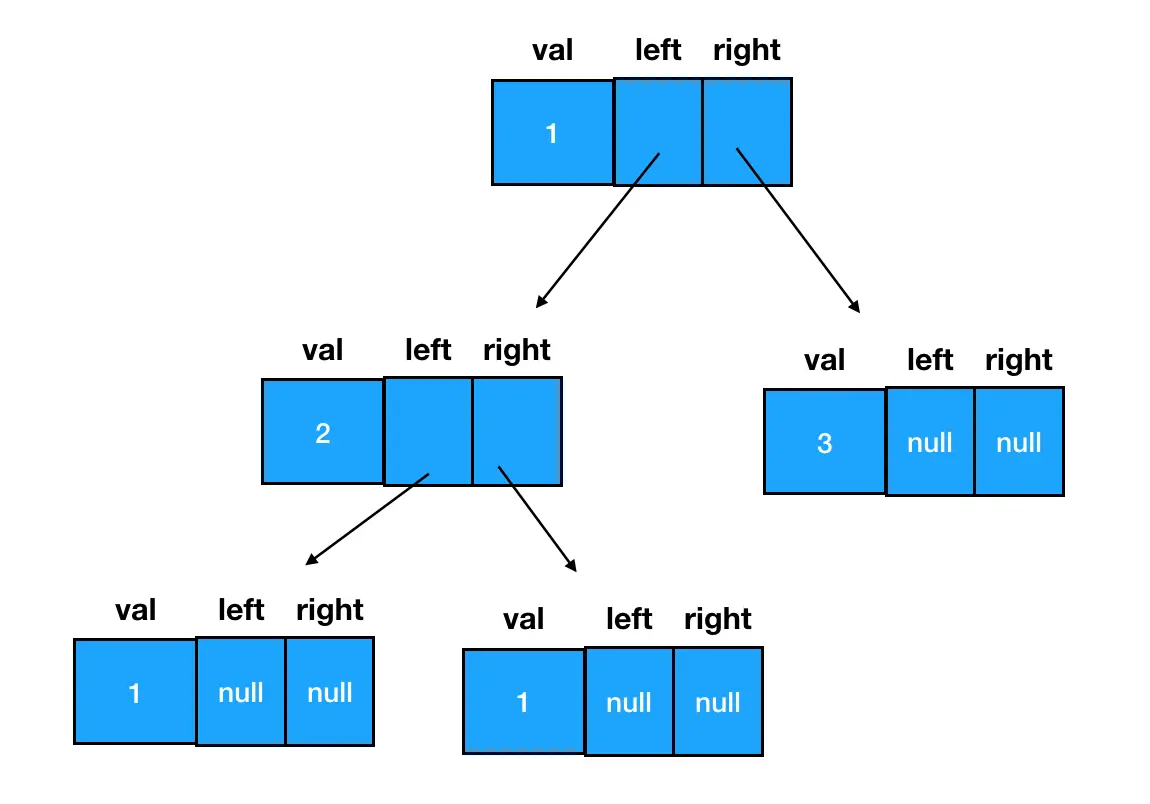
现在各位已经掌握了做二叉树面试题所需要的一系列前置知识。接下来我会带大家一起通过写代码的方式，来搞定二叉树系列里最首当其冲、同时相当热门的考点------二叉树的遍历。

（阅读过程中有任何想法或疑问，或者单纯希望和笔者交个朋友啥的，欢迎大家添加我的微信xyalinode与我交流哈~） <math xmlns="http://www.w3.org/1998/Math/MathML"> 保姆式教学の 温情提示： \color{LightPink}{保姆式教学の}\color{Pink}{温情提示：} </math>保姆式教学の温情提示：

我们之前学过数组的遍历、链表的遍历，这些线性结构的遍历考起来没有什么难度，可以理解为基本技能，一般也不会单独出题。

但是二叉树可不一样了，这一"开叉"，它的遍历难度陡然上了一个台阶。在面试中，二叉树的各种姿势的遍历，是非常容易作为独立命题点来考察的 ，而且这个考察的频率极高极高。

因此对于有志于在算法面试上求稳的同学，本节涉及的编码内容，你千万不要沉溺在"我看懂了"、"我理解了"、"我知道你说的是啥意思了"这种虚无的成就感中------假的，都是假的，只有自己写出来的代码才是真的！

理解只是记忆的前提，只吹理解不记忆，不如回家去种地：）。

这里我对大家的要求就是"在理解的基础上记忆 "。如果你真的暂时理解不了，背也要先给你自己背下来，然后带着对正确思路的记忆，重新去看解析部分里的图文（尤其是图）、反复去理解，这么整下来你不可能学不会。

面试时见到二叉树的遍历，你不能再去想太多------没有那么多时间给你现场推理，这么熟悉的题目你没必要现场推理，你要做的是默写！默写啊！老哥们！！（捶胸顿足）

二叉树的遍历------命题思路解读

以一定的顺序规则，逐个访问二叉树的所有结点，这个过程就是二叉树的遍历。按照顺序规则的不同，遍历方式有以下四种：

• 先序遍历
• 中序遍历
• 后序遍历
• 层次遍历

按照实现方式的不同，遍历方式又可以分为以下两种：

• 递归遍历（先、中、后序遍历）
• 迭代遍历（层次遍历）

层次遍历的考察相对比较孤立，我们会把它放在后续的真题归纳解读环节来讲。这里我们重点要看的是先、中、后序遍历三兄弟------由于同时纠结了二叉树和"递归"两个大热命题点，又不属于"偏难怪"之流，遍历三兄弟一直是前端算法面试官们的心头好，考察热度经久不衰。

递归遍历初相见

编程语言中，函数Func(Type a,......)直接或间接调用函数本身，则该函数称为递归函数。

简单来说，当我们看到一个函数反复调用它自己的时候，递归就发生了。"递归"就意味着"反复"，像咱们之前对二叉树的定义，就可以理解为是一个递归式的定义：

• 它可以没有根结点，作为一棵空树存在
• 如果它不是空树，那么必须由根结点、左子树和右子树组成，且左右子树都是二叉树。

这个定义有着这样的内涵：如果我们想要创建一个二叉树结点作为根结点，那么它左侧的子结点和右侧的子结点也都必须符合二叉树结点的定义，这意味着我们要反复地执行"创建一个由数据域、左右子树组成的结点"这个动作，直到数据被分配完为止。

结合这个定义来看，每一棵二叉树都应该由这三部分组成：

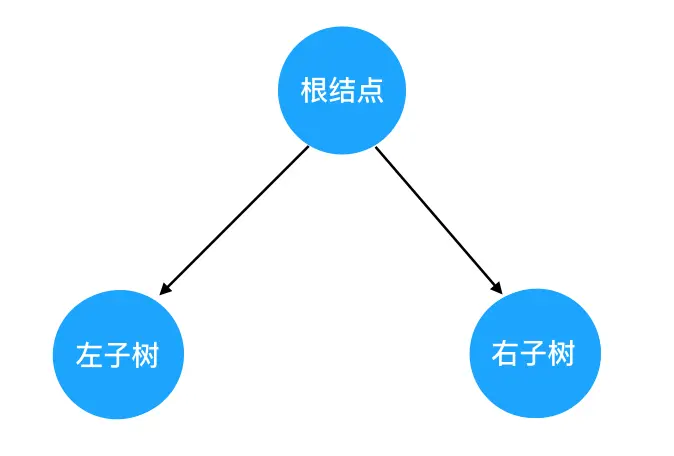对树的遍历，就可以看做是对这三个部分的遍历。这里就引出一个问题：三个部分中，到底先遍历哪个、后遍历哪个呢？我们此处其实可以穷举一下，假如在保证"左子树一定先于右子树遍历"这个前提，那么遍历的可能顺序也不过三种：

• 根结点 -> 左子树 -> 右子树
• 左子树 -> 根结点 -> 右子树
• 左子树 -> 右子树 -> 根结点

上述三个遍历顺序，就分别对应了二叉树的先序遍历、中序遍历和后序遍历规则。

在这三种顺序中，根结点的遍历分别被安排在了首要位置、中间位置和最后位置。

所谓的"先序"、"中序"和"后序"，"先"、"中"、"后"其实就是指根结点的遍历时机。

遍历方法图解与编码实现

先序遍历

先序遍历的"旅行路线"如下图红色数字 所示：

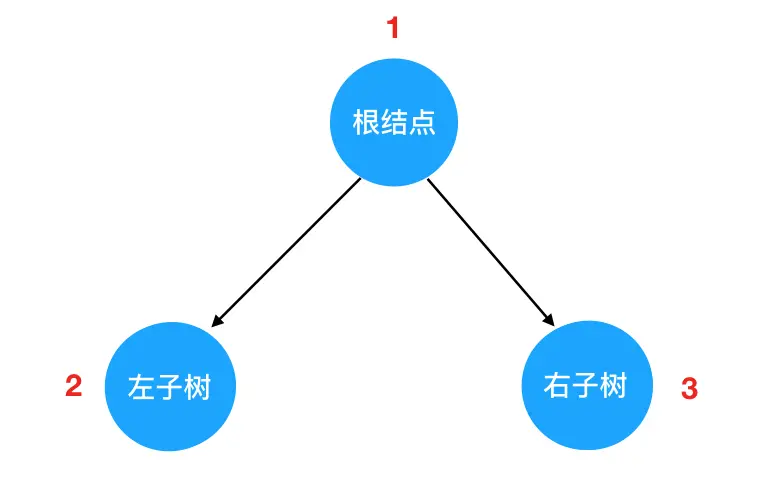
如果说有 N 多个子树，那么我们在每一棵子树内部，都要重复这个"旅行路线"，动画演示如下：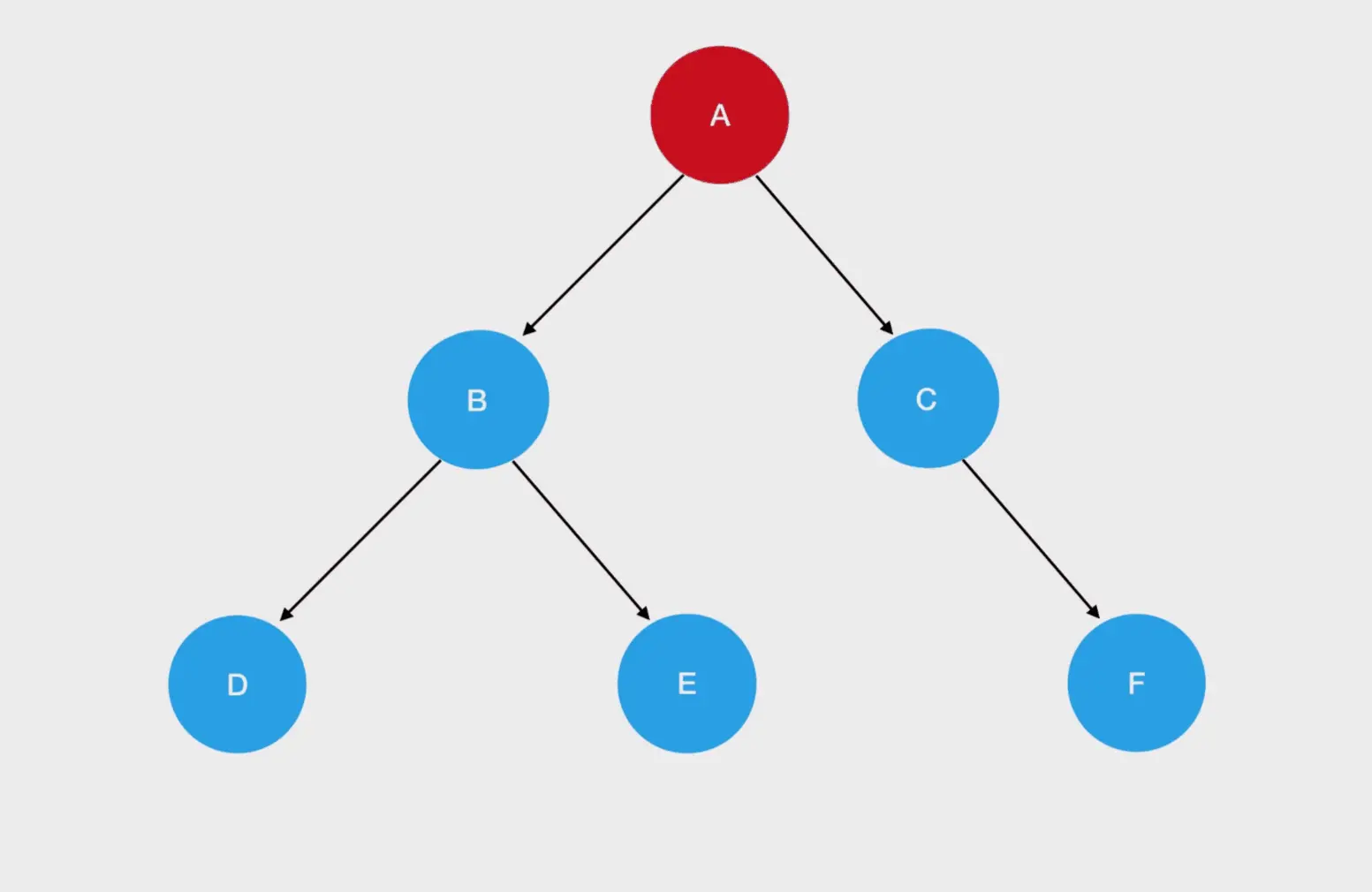

这个"重复"，我们就用递归来实现。

注：上面这个二叉树的结构，大家可以试着用我们前面学过的知识编码实现一把。这里为了方便大家理解，我直接给出来了哈（记得自己回去也要试着手写一遍）：

const root = {
  val: "A",
  left: {
    val: "B",
    left: {
      val: "D"
    },
    right: {
      val: "E"
    }
  },
  right: {
    val: "C",
    right: {
      val: "F"
    }
  }
};

递归函数的编写要点

编写一个递归函数之前，大家首先要明确两样东西：

• 递归式
• 递归边界

递归式，它指的是你每一次重复的内容是什么。在这里，我们要做先序遍历，那么每一次重复的其实就是 根结点 -> 左子树 -> 右子树 这个旅行路线。

递归边界，它指的是你什么时候停下来 。

在遍历的场景下，当我们发现遍历的目标树为空的时候，就意味着旅途已达终点、需要画上句号了。这个"画句号"的方式，在编码实现里对应着一个 return 语句------这就是二叉树遍历的递归边界。

第一个递归遍历函数

上面咱们已经捋清楚思路，接下来话不多说，先序遍历的编码实现：

// 所有遍历函数的入参都是树的根结点对象
function preorder(root) {
    // 递归边界，root 为空
    if(!root) {
        return 
    }
     
    // 输出当前遍历的结点值
    console.log('当前遍历的结点值是：', root.val)  
    // 递归遍历左子树 
    preorder(root.left)  
    // 递归遍历右子树  
    preorder(root.right)
}

不熟悉这种写法？不用怕，我们接下来一行一行把这段代码跑完，你就知道它在干啥了：

图解先序遍历的完整过程

各位现在完全可以再回过头来看一下我们前面示例的这棵二叉树：

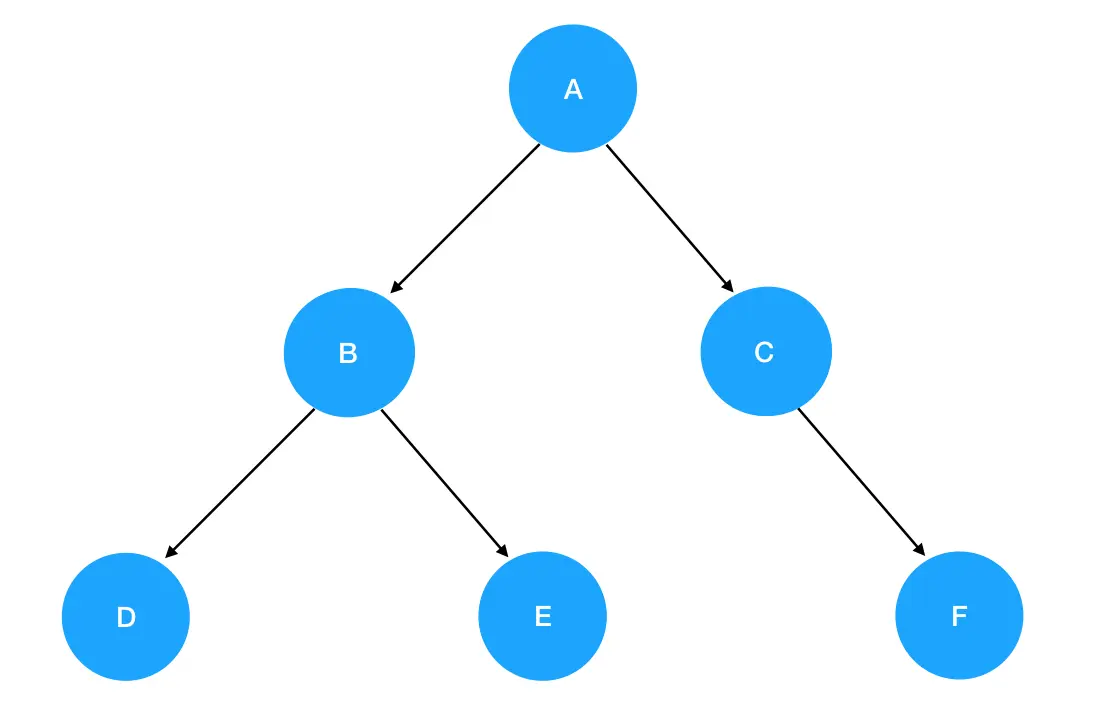
我们直接把它套进 preorder 函数里，一步一步来认清楚先序遍历的每一步做了什么：

1. 调用 preorder(root)，这里 root 就是 A，它非空，所以进入递归式，输出 A 值。接着优先遍历左子树，preorder(root.left) 此时为 preorder(B) ：

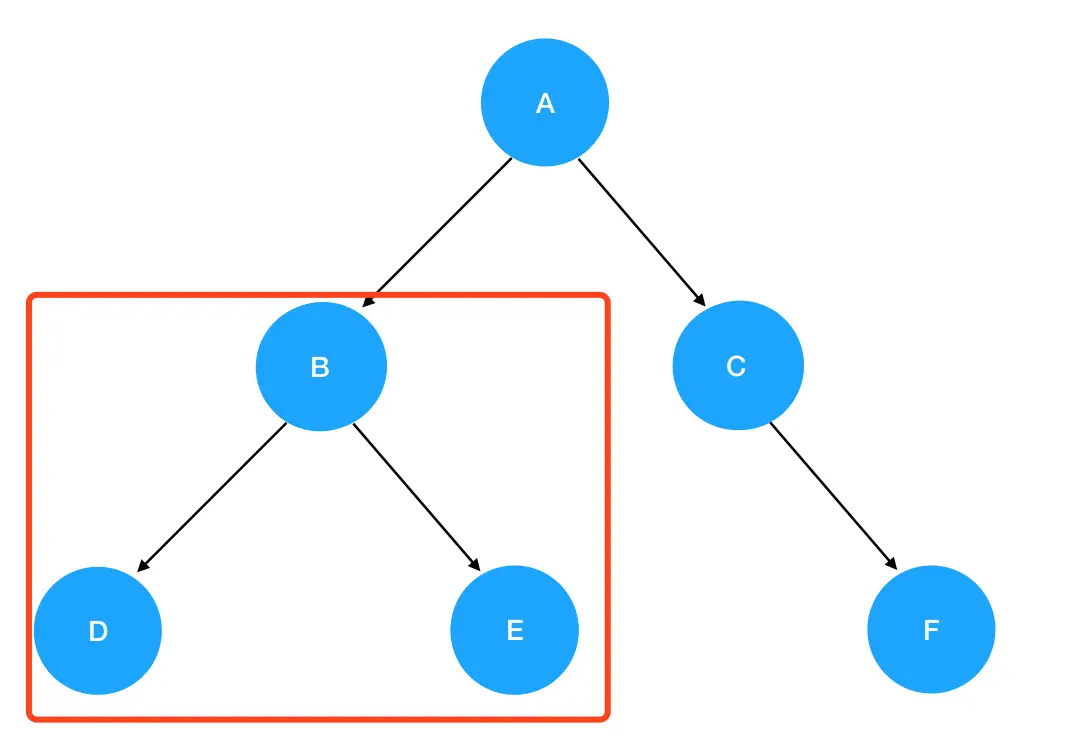2. 进入 preorder(B) 的逻辑： 入参为结点 B，非空，进入递归式，输出 B 值。接着优先遍历 B 的左子树，preorder(root.left) 此时为 preorder(D) ：

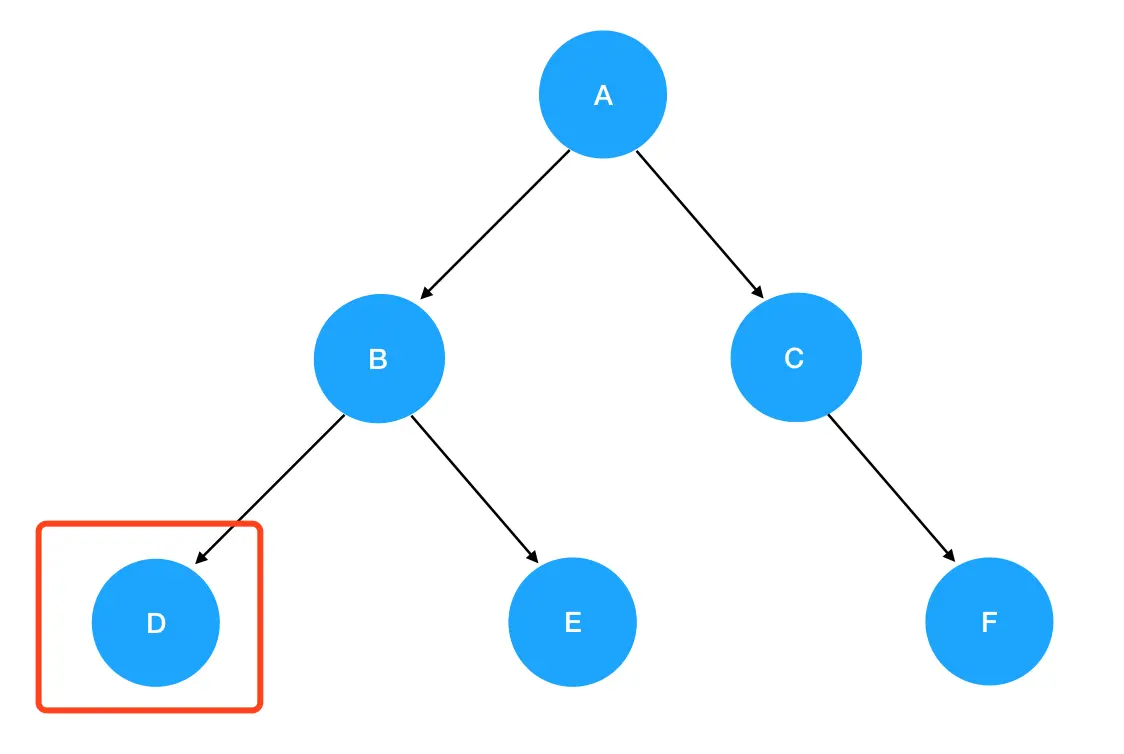
3. 进入 preorder(D) 的逻辑： 入参为结点 D，非空，进入递归式，输出 D 值。接着优先遍历 D 的左子树，preorder(root.left) 此时为 preorder(null)：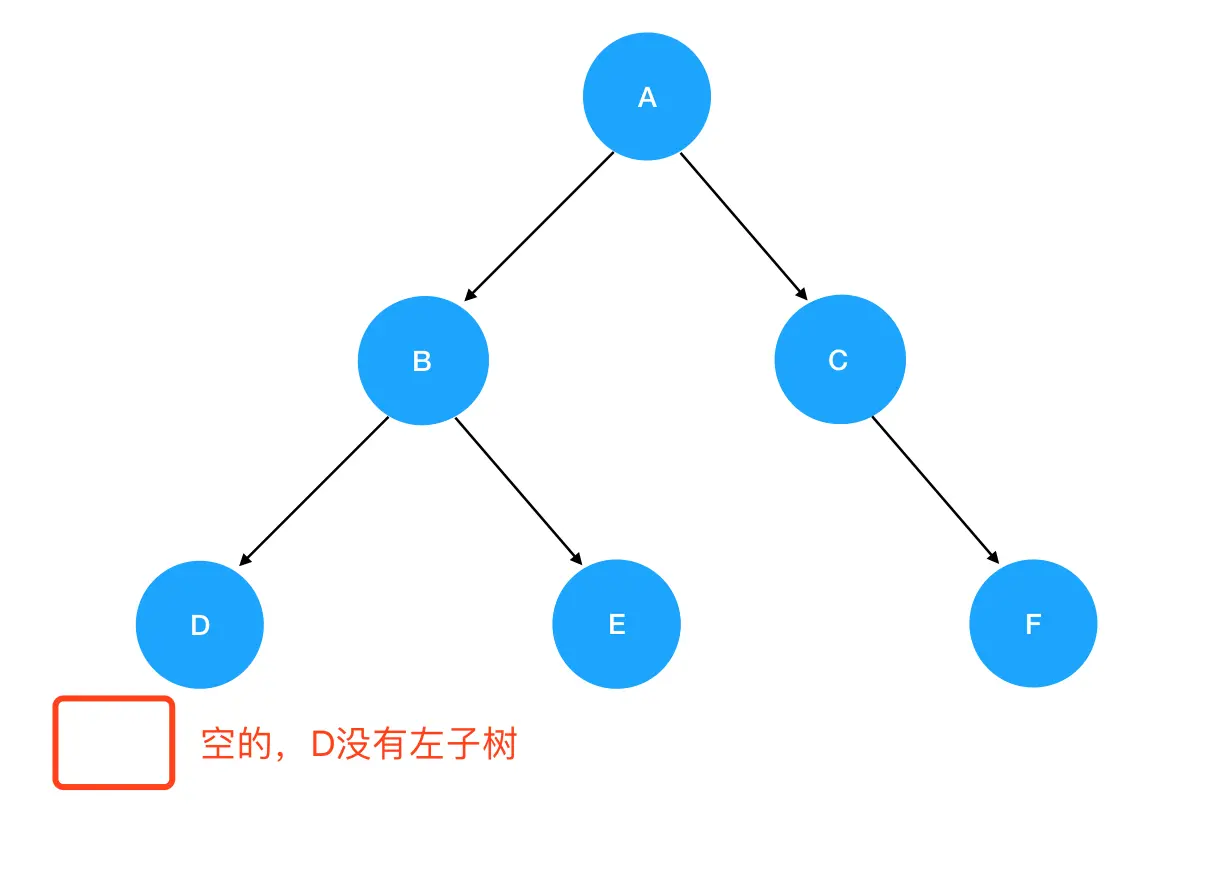

4. 进入preorder(null) ，发现抵达了递归边界，直接 return 掉。紧接着是 preorder(D) 的逻辑往下走，走到了 preorder(root.right) ：

5. 再次进入preorder(null) ，发现抵达了递归边界，直接 return 掉，回到preorder(D) 里。接着 preorder(D) 的逻辑往下走，发现 preorder(D) 已经执行完了。于是返回，回到preorder(B) 里，接着preorder(B) 往下走，进入 preorder(root.right) ，也就是 preorder(E) ：

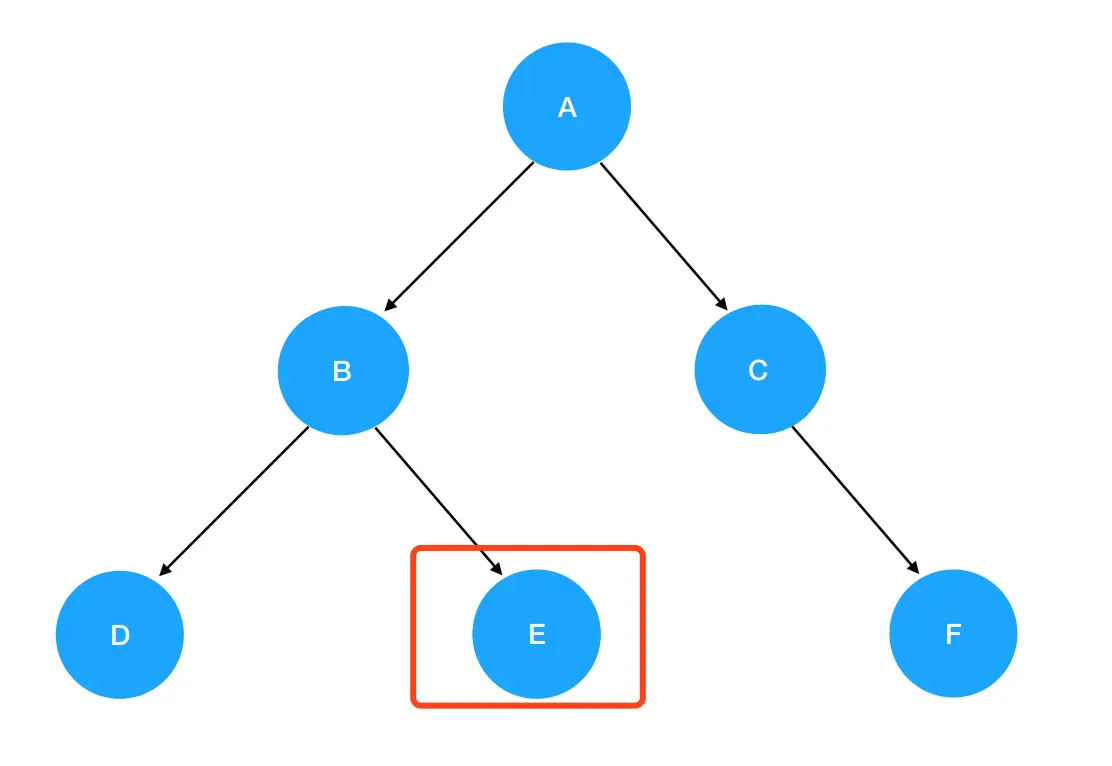
E 不为空，进入递归式，输出 E 值。接着优先遍历 E 的左子树，preorder(root.left) 此时为 preorder(null)，触碰递归边界，直接返回 preorder(E)；继续preorder(E)执行下去，是preorder(root.right) ，这里 E 的 right 同样是 null，故直接返回。如此一来，preorder(E)就执行完了，回到preorder(B)里去；发现preorder(B)也执行完了，于是回到preorder(A)里去，执行preorder(A)中的 preorder(root.right)。

6. root 是A，root.right 就是 C 了，进入preorder(C)的逻辑：

C 不为空，进入递归式，输出 C 值。接着优先遍历 C 的左子树，preorder(root.left) 此时为 preorder(null)，触碰递归边界，直接返回。继续preorder(C)执行下去，是preorder(root.right) ，这里 C 的 right 是 F：

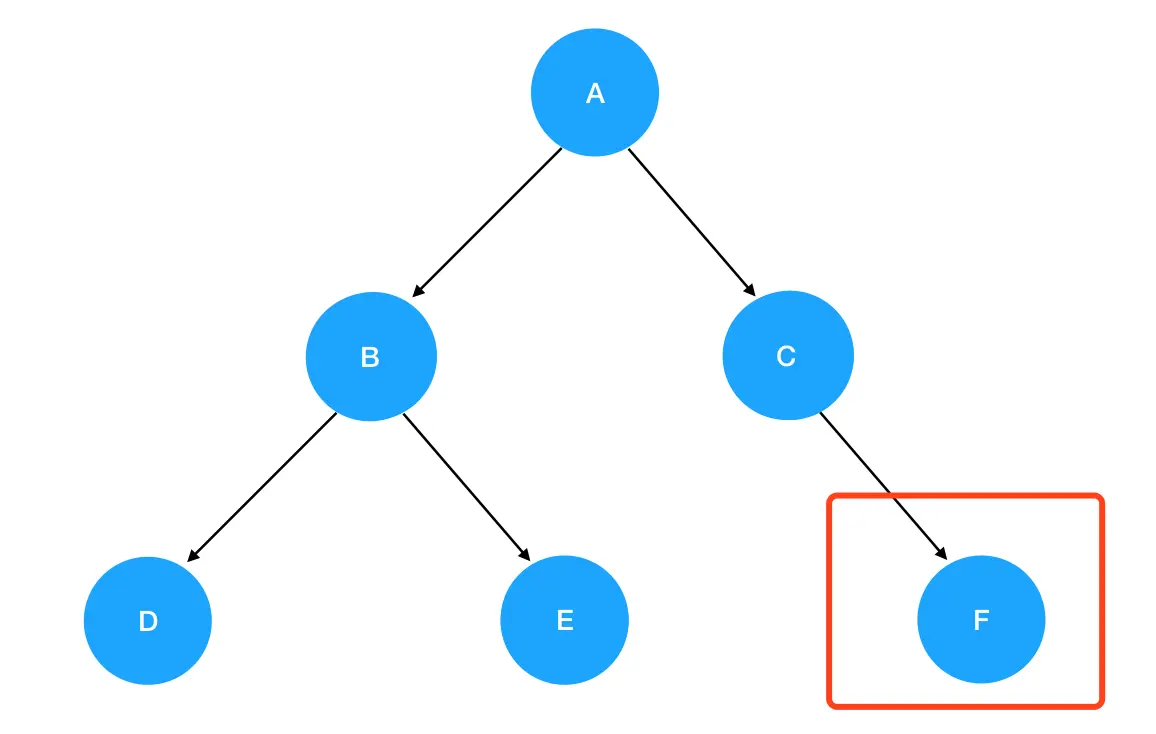7. 进入preorder(F)的逻辑，F 不为空，进入递归式，输出 F 值。接着优先遍历 F 的左子树，preorder(root.left) 此时为 preorder(null)，触碰递归边界，直接返回 preorder(F)；继续preorder(F)执行下去，是preorder(root.right) ，这里 F 的 right 同样是 null，故直接返回preorder(F)。此时preorder(F)已经执行完了，返回preorder(C)；发现preorder(C)也执行完了，就回到 preorder(A)；发现preorder(A)作为递归入口，它的逻辑也已经执行完了，于是我们的递归活动就正式画上了句号。到此为止，6个结点也已全部按照先序遍历顺序输出：

当前遍历的结点值是： A
当前遍历的结点值是： B
当前遍历的结点值是： D
当前遍历的结点值是： E
当前遍历的结点值是： C
当前遍历的结点值是： F

中序遍历

理解了先序遍历的过程，中序遍历就不是什么难题。唯一的区别只是把遍历顺序调换了左子树 -> 根结点 -> 右子树：

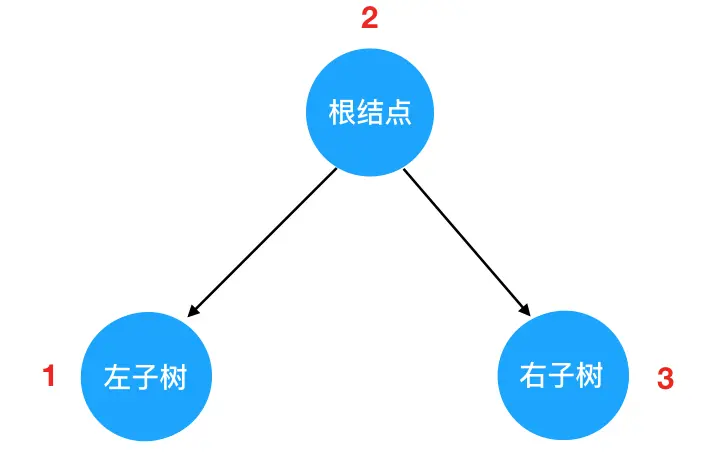若有多个子树，那么我们在每一棵子树内部，都要重复这个"旅行路线"，这个过程用动画表示如下：

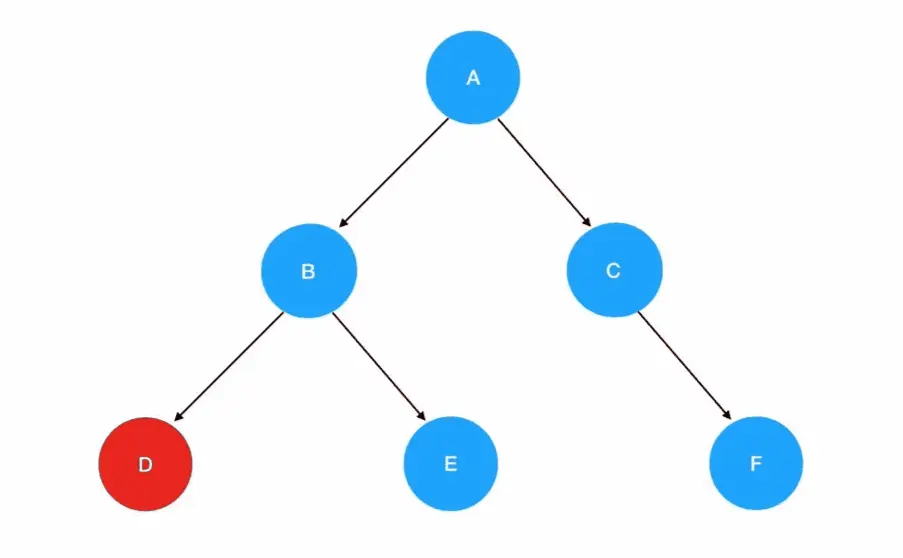
递归边界照旧，唯一发生改变的是递归式里调用递归函数的顺序------左子树的访问会优先于根结点。我们参考先序遍历的分析思路，来写中序遍历的代码：

// 所有遍历函数的入参都是树的根结点对象
function inorder(root) {
    // 递归边界，root 为空
    if(!root) {
        return 
    }
     
    // 递归遍历左子树 
    inorder(root.left)  
    // 输出当前遍历的结点值
    console.log('当前遍历的结点值是：', root.val)  
    // 递归遍历右子树  
    inorder(root.right)
}

按照中序遍历的逻辑，同样的一棵二叉树，结点内容的输出顺序如下：

当前遍历的结点值是： D
当前遍历的结点值是： B
当前遍历的结点值是： E
当前遍历的结点值是： A
当前遍历的结点值是： C
当前遍历的结点值是： F

后序遍历

在后序遍历中，我们先访问左子树，再访问右子树，最后访问根结点：
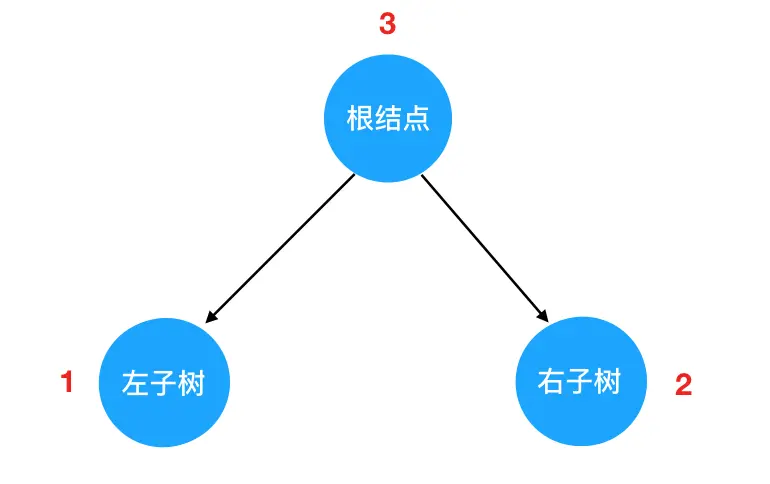若有多个子树，那么我们在每一棵子树内部，都要重复这个"旅行路线"：

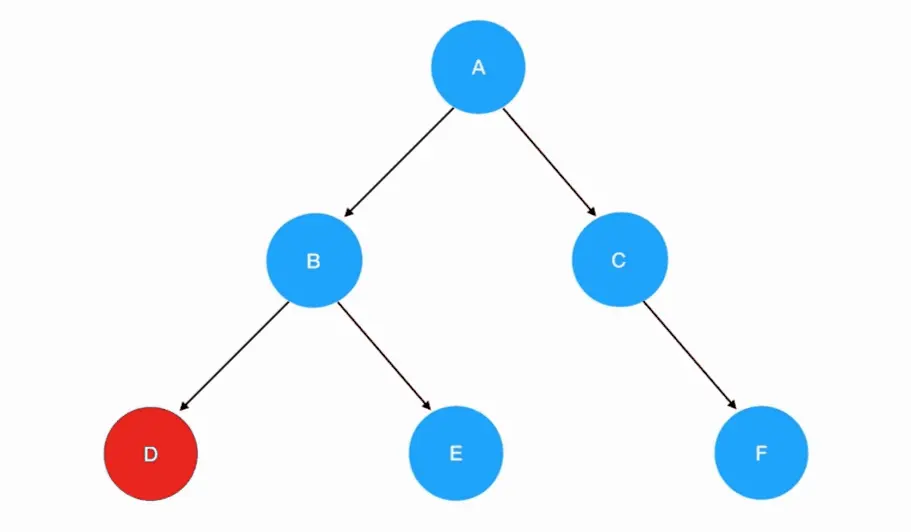在编码实现的时候，递归边界照旧，唯一发生改变的仍然是是递归式里调用递归函数的顺序：

function postorder(root) {
    // 递归边界，root 为空
    if(!root) {
        return 
    }
     
    // 递归遍历左子树 
    postorder(root.left)  
    // 递归遍历右子树  
    postorder(root.right)
    // 输出当前遍历的结点值
    console.log('当前遍历的结点值是：', root.val)  
}

按照后序遍历的逻辑，同样的一棵二叉树，结点内容的输出顺序如下：

当前遍历的结点值是： D
当前遍历的结点值是： E
当前遍历的结点值是： B
当前遍历的结点值是： F
当前遍历的结点值是： C
当前遍历的结点值是： A

结语

对于二叉树的先、中、后序遍历，各位只要掌握了其中一种的思路，就可以举一反三、顺势推导其它三种思路。不过，我个人的建议，仍然是以"默写"的标准来要求自己，面试时不要指望"推导"，而应该有条件反射。这样才可以尽量地提高你做题的效率，为后面真正的难题、综合性题目腾出时间。

关于二叉树遍历类题目的讨论，这里只是一个开始。二叉树的先、中、后包括层次遍历的玩法，还有很多很多，我们在后续的真题归纳解读专题、包括末尾的大规模刷题训练中，会带大家认识更多新奇好玩的东西。

（阅读过程中有任何想法或疑问，或者单纯希望和笔者交个朋友啥的，欢迎大家添加我的微信xyalinode与我交流哈~） 结束了数据结构基本功的学习，接下来在真正开始撸真题之前，大家还需要具备评价算法的能力。

平时我们定义一个人是否"懂行"，一个重要的依据就是看这个人对某一个事物是否具备正确的评价能力。

举个例子，同样是买手机，外行进到手机店，他关注的可能是手机有没有跑马灯、有没有皮套护体、有没有"八心八箭"------这些东西，任何一部手机随便包装一下就都有了，根本没法反映出这台手机的本质问题。但如果是一个相对懂手机的人，他可能就会去关注这台手机的芯片、内存、屏幕材质及分辨率等等，从而对手机的整体性能和质量作出一个合理的判断，这样他买到好手机的概率就更大。

回到做算法题上，也是一样的道理。在面试时，自己给出的算法到底过不过得去，这一点在面试官给出评语之前，自己就应该有所感知。做到这一点，你才会掌握改进算法的主动权。

本节我们要学习的就是评价算法的两个重要依据------时间复杂度和空间复杂度。

很多同学算法入门直接就跪在复杂度理解这一环。时间复杂度、空间复杂度，直接读概念确实太无聊，我们本节从代码入手，大家的理解会更直观一点。

时间复杂度

大家先来看这样一个问题：下面这段代码，一共会执行多少次？

function traverse(arr) {
    var len = arr.length
    for(var i=0;i<len;i++) {
        console.log(arr[i])
    }
}

首先，最没有悬念的是函数里的第一行代码，它只会被执行1次：

var len = arr.length

其次没有悬念的是循环体：

console.log(arr[i])

for循环跑了 n 次，因此这条语句就会被执行 n 次。

循环体上面的几个部分我们拆开来看，首先是 i 的初始化语句：

var i = 0

初始化只有1次，因此它也只会被执行1次。

接着是 i < len 这个判断。这里有个规律大家可以记下：在所有的 for 循环里，判断语句都会比递增语句多执行一次。在这里，判断语句执行的次数就是 n+1。

再往下就是递增语句 i++ 了，它跟随整个循环体，毫无疑问会被执行 n 次。

假如把总的执行次数记为 T(n)，下面咱们就可以来做个简单的加法：

T(n) = 1 + n + 1 + (n+1) + n = 3n + 3

接下来我们看看规模为 n*n 的二维数组的遍历，一共需要执行多少次代码：

function traverse(arr) {
    var outLen = arr.length

    for(var i=0;i<outLen;i++) {
        var inLen = arr[i].length

        for(var j=0;j<inLen;j++) { 
            console.log(arr[i][j])
        }
    }
}

首先仍然是没有悬念的第一行代码，它只会被执行一次：

var outLen = arr.length

接下来我们来看最内层的循环体：

console.log(arr[i][j])

因为咱们是两层循环，所以这货会被执行 n*n = n^2 次。

其它语句的计算思路和咱们第一个🌰区别不大，这里我就不重复讲了，直接给出大家答案：

继续来做个求总执行次数 T(n) 的加法看看：

T(n) = 1 + 1 + (n+1) + n + n + n + n*(n+1) + n*n + n*n = 3n^2 + 5n + 3

代码的执行次数，可以反映出代码的执行时间。但是如果每次我们都逐行去计算 T(n)，事情会变得非常麻烦。算法的时间复杂度，它反映的不是算法的逻辑代码到底被执行了多少次，而是随着输入规模的增大，算法对应的执行总次数的一个变化趋势。要想反映趋势，那就简单多了，直接抓主要矛盾就行。我们可以尝试对 T(n) 做如下处理：

• 若 T(n) 是常数，那么无脑简化为1
• 若 T(n) 是多项式，比如 3n^2 + 5n + 3，我们只保留次数最高那一项，并且将其常数系数无脑改为1。

经过这么一波操作，T(n) 就被简化为了 O(n)：

T(n) = 10  
O(n) = 1

T(n) = 3n^2 + 5n + 3
O(n) = n^2

到这里，我们思路仍然是 计算T(n) -> 推导O(n)。这么讲是为了方便大家理解 O(n) 的简化过程，实际操作中，O(n) 基本可以目测，比如咱们上面的两个遍历函数：

function traverse1(arr) {
    var len = arr.length
    for(var i=0;i<len;i++) {
        console.log(arr[i])
    }
}

function traverse2(arr) {
    var outLen = arr.length

    for(var i=0;i<outLen;i++) {
        var inLen = arr[i].length

        for(var j=0;j<inLen;j++) { 
            console.log(arr[i][j])
        }
    }
}

遍历 N 维数组，需要 N 层循环，我们只需要关心其最内层那个循环体被执行多少次就行了。

我们可以看出，规模为 n 的一维数组遍历时，最内层的循环会执行 n 次，其对应的时间复杂度是 O(n)；规模为 n*n 的二维数组遍历时，最内层的循环会执行 n*n 次，其对应的时间复杂度是 O(n^2)。

以此类推，规模为 n*m 的二维数组最内层循环会执行 n*m 次，其对应的时间复杂度就是 O(n*m)；规模为 n*n*n 的三维数组最内层循环会执行 n^3 次，因此其对应的时间复杂度就表示为 O(n^3)。

常见的时间复杂度表达，除了多项式以外，还有logn。我们一起来看另一个算法：

function fn(arr) {
    var len = arr.length  
    
    for(var i=1;i<len;i=i*2) {
        console.log(arr[i])
    }
}

这个算法读取一个一维数组作为入参，然后对其中的元素进行跳跃式的输出。这个跳跃的规则，就是数组下标从1开始，每次会乘以二。

如何计算这个函数的时间复杂度呢？在有循环的地方，我们关心的永远是最内层的循环体。这个算法中，我们关心的就是 console.log(arr[i]) 到底被执行了几次，换句话说，也就是要知道 i<n（ len === n） 这个条件是在 i 递增多少次后才不成立的。

假设 i 在以 i=i*2的规则递增了 x 次之后，i<n 开始不成立（反过来说也就是 i>=n 成立）。那么此时我们要计算的其实就是这样一个数学方程：

2^x >= n

x解出来，就是要大于等于以 2 为底数的 n 的对数：

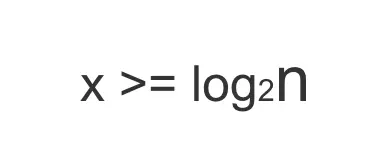
也就是说，只有当 x 小于 log2n 的时候，循环才是成立的、循环体才能执行。注意涉及到对数的时间复杂度，底数和系数都是要被简化掉的。那么这里的 O(n) 就可以表示为：

O(n) = logn

没错，这时的主要矛盾，就变成了一个对数表达式。

关于常见的时间复杂度，我们会在后面讲到具体知识点（尤其是排序算法）时，结合实例来给大家做分析。这里大家首先要认识一下常见时间复杂度有哪些，并且对这些常见时间复杂度之间的大小关系做个把握。

常见的时间复杂度按照从小到大的顺序排列，有以下几种：

空间复杂度

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。和时间复杂度相似，它是内存增长的趋势 。

常见的空间复杂度有 O(1)、O(n) 和 O(n^2)。

理解空间复杂度，我们照样来看一个🌰：

function traverse(arr) {
    var len = arr.length
    for(var i=0;i<len;i++) {
        console.log(arr[i])
    }
}

在 traverse 中，占用空间的有以下变量：

arr    
len   
i    

后面尽管咱们做了很多次循环，但是这些都是时间上的开销。循环体在执行时，并没有开辟新的内存空间。因此，整个 traverse 函数对内存的占用量是恒定的，它对应的空间复杂度就是 O(1)。

下面我们来看另一个🌰，此时我想要初始化一个规模为 n 的数组，并且要求这个数组的每个元素的值与其索引始终是相等关系，我可以这样写：

function init(n) {
    var arr = []
    for(var i=0;i<n;i++) {
        arr[i] = i
    }
    return arr
}

在这个 init 中，涉及到的占用内存的变量有以下几个：

n 
arr
i

注意这里这个 arr，它并不是一个一成不变的数组。arr最终的大小是由输入的 n 的大小决定的，它会随着 n 的增大而增大、呈一个线性关系。因此这个算法的空间复杂度就是 O(n)。

由此我们不难想象，假如需要初始化的是一个规模为 n*n 的数组，那么它的空间复杂度就是 O(n^2) 啦。

小结

结束了本节的学习，相信各位对时间复杂度和空间复杂度都有了一个感性的认知和初步的了解。在后续的学习中，我们会在必要的时候继续为大家提点真题中的时间复杂度和空间复杂度，带领大家在实战中强化对理论概念的认知。

（阅读过程中有任何想法或疑问，或者单纯希望和笔者交个朋友啥的，欢迎大家添加我的微信xyalinode与我交流哈~） 我们现在要开始做题啦！

万里长征第一步，仍然是数组。

单纯针对数组来考察的题目，总体来说，都不算太难------数组题目要想往难了出，基本都要结合排序、二分和动态规划这些相对复杂的算法思想才行。

咱们本节要解决的正是这一类"不算太难"的数组题目------并不是只有难题才拥有成为真题的入场券，一道好题不一定会难，它只要能够反映问题就可以了。

本节所涉及的题目在面试中普遍具有较高的出镜率、同时兼具一定的综合性，对培养大家的通用解题能力大有裨益 。

相信这节你会学得很开心，在轻松中收获自己的第一份算法解题锦囊。

Map 的妙用------两数求和问题

真题描述： 给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，你不能重复利用这个数组中同样的元素。
示例: 给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9 所以返回 [0, 1]

思路分析：

一个"淳朴"的解法

这道题相信很多同学看一眼就很快能得出一个最基本的思路：两层循环来遍历同一个数组；第一层循环遍历的值记为 a，第二层循环时遍历的值记为 b；若 a+b = 目标值，那么 a 和 b 对应的数组下标就是我们想要的答案。

对"淳朴"解法的反思

大家以后做算法题的时候，要有这样的一种本能：当发现自己的代码里有两层循环时，先反思一下，能不能用空间换时间，把它优化成一层循环。

因为两层循环很多情况下都意味着 O(n^2) 的复杂度，这个复杂度非常容易导致你的算法超时。即便没有超时，在明明有一层遍历解法的情况下，你写了两层遍历，面试官对你的印象分会大打折扣。

空间换时间，Map 来帮忙

拿我们这道题来说，其实二层遍历是完全不必要的。

大家记住一个结论：几乎所有的求和问题，都可以转化为求差问题。 这道题就是一个典型的例子，通过把求和问题转化为求差问题，事情会变得更加简单。

我们可以在遍历数组的过程中，增加一个 Map 来记录已经遍历过的数字及其对应的索引值。然后每遍历到一个新数字的时候，都回到 Map 里去查询 targetNum 与该数的差值是否已经在前面的数字中出现过了。若出现过，那么答案已然显现，我们就不必再往下走了。

我们以 nums = [2, 7, 11, 15] 这个数组为例，来模拟一下这个思路：

第一次遍历到 2，此时 Map 为空：

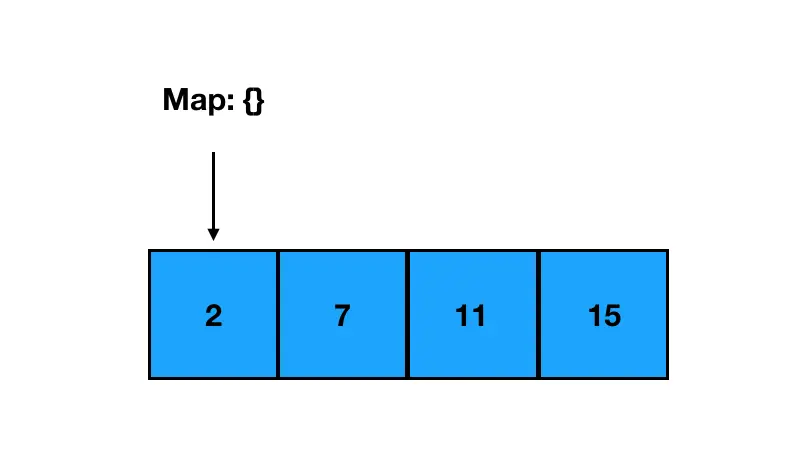
以 2 为 key，索引 0 为 value 作存储，继续往下走；遇到了 7：

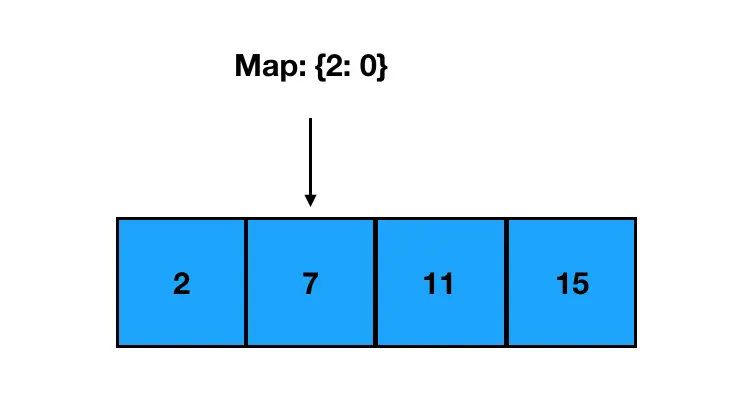
计算 targetNum 和 7 的差值为2，去 Map 中检索 2 这个 key，发现是之前出现过的值：

那么 2 和 7 的索引组合就是这道题的答案啦。

键值对存储我们可以用 ES6 里的 Map 来做，如果图省事，直接用对象字面量来定义也没什么问题。

编码实现

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
const twoSum = function(nums, target) {
    // 这里我用对象来模拟 map 的能力
    const diffs = {}
    // 缓存数组长度
    const len = nums.length
    // 遍历数组
    for(let i=0;i<len;i++) {
        // 判断当前值对应的 target 差值是否存在（是否已遍历过）
        if(diffs[target-nums[i]]!==undefined) {
            // 若有对应差值，那么答案get！
            return [diffs[target - nums[i]], i]
        }
        // 若没有对应差值，则记录当前值
        diffs[nums[i]]=i
    }
};

tips：这道题也可以用 ES6 中的 Map 来做，你试试呢？

强大的双指针法

合并两个有序数组

真题描述：给你两个有序整数数组 nums1 和 nums2，请你将 nums2 合并到 nums1 中，使 nums1 成为一个有序数组。

说明: 初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。 你可以假设 nums1 有足够的空间（空间大小大于或等于 m + n）来保存 nums2 中的元素。
示例: 输入:

nums1 = [1,2,3,0,0,0], m = 3

nums2 = [2,5,6], n = 3

输出: [1,2,2,3,5,6]

思路分析

标准解法

这道题没有太多的弯弯绕绕，标准解法就是双指针法。首先我们定义两个指针，各指向两个数组生效部分的尾部：

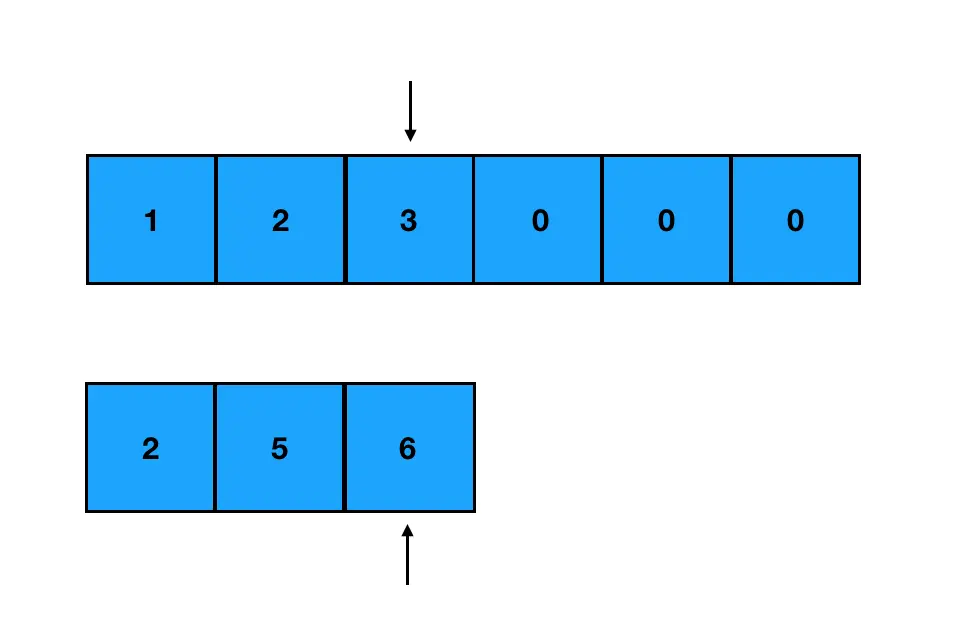
每次只对指针所指的元素进行比较。取其中较大的元素，把它从 nums1 的末尾往前面填补：

这里有一点需要解释一下：

为什么是从后往前填补？因为是要把所有的值合并到 nums1 里，所以说我们这里可以把 nums1 看做是一个"容器"。但是这个容器，它不是空的，而是前面几个坑有内容的。如果我们从前往后填补，就没法直接往对应的坑位赋值了（会产生值覆盖）。

从后往前填补，我们填的都是没有内容的坑，这样会省掉很多麻烦。

由于 nums1 的有效部分和 nums2 并不一定是一样长的。我们还需要考虑其中一个提前到头的这种情况：

1. 如果提前遍历完的是 nums1 的有效部分，剩下的是 nums2。那么这时意味着 nums1 的头部空出来了，直接把 nums2 整个补到 nums1 前面去即可。

2. 如果提前遍历完的是 nums2，剩下的是 nums1。由于容器本身就是 nums1，所以此时不必做任何额外的操作。

编码实现：

/**
 * @param {number[]} nums1
 * @param {number} m
 * @param {number[]} nums2
 * @param {number} n
 * @return {void} Do not return anything, modify nums1 in-place instead.
 */
const merge = function(nums1, m, nums2, n) {
    // 初始化两个指针的指向，初始化 nums1 尾部索引k
    let i = m - 1, j = n - 1, k = m + n - 1
    // 当两个数组都没遍历完时，指针同步移动
    while(i >= 0 && j >= 0) {
        // 取较大的值，从末尾往前填补
        if(nums1[i] >= nums2[j]) {
            nums1[k] = nums1[i] 
            i-- 
            k--
        } else {
            nums1[k] = nums2[j] 
            j-- 
            k--
        }
    }
    
    // nums2 留下的情况，特殊处理一下 
    while(j>=0) {
        nums1[k] = nums2[j]  
        k-- 
        j--
    }
};

找点乐子：

上面我们给出的，是面试官最喜欢看到的一种解法，这种解法适用于各种语言。

但是就 JS 而言，我们还可以"另辟蹊径"，仔细想想，你有什么妙招？

三数求和问题

双指针法能处理的问题多到你想不到。不信来瞅瞅两数求和它儿子------三数求和问题！

俗话说，青出于蓝而胜于蓝，三数求和虽然和两数求和只差了一个字，但是思路却完全不同。

真题描述：给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。
示例： 给定数组 nums = [-1, 0, 1, 2, -1, -4]， 满足要求的三元组集合为： [ [-1, 0, 1], [-1, -1, 2] ]

思路分析

三数之和延续两数之和的思路，我们可以把求和问题变成求差问题------固定其中一个数，在剩下的数中寻找是否有两个数和这个固定数相加是等于0的。

虽然乍一看似乎还是需要三层循环才能解决的样子，不过现在我们有了双指针法，定位效率将会被大大提升，从此告别过度循环~

（这里大家相信已经能察觉出来双指针法的使用场景了，一方面，它可以做到空间换时间；另一方面，它也可以帮我们降低问题的复杂度。）

双指针法用在涉及求和、比大小类的数组题目里时，大前提往往是：该数组必须有序。否则双指针根本无法帮助我们缩小定位的范围，压根没有意义。因此这道题的第一步是将数组排序：

 nums = nums.sort((a,b)=>{
    return a-b
})

然后，对数组进行遍历，每次遍历到哪个数字，就固定哪个数字。然后把左指针指向该数字后面一个坑里的数字，把右指针指向数组末尾，让左右指针从起点开始，向中间前进：

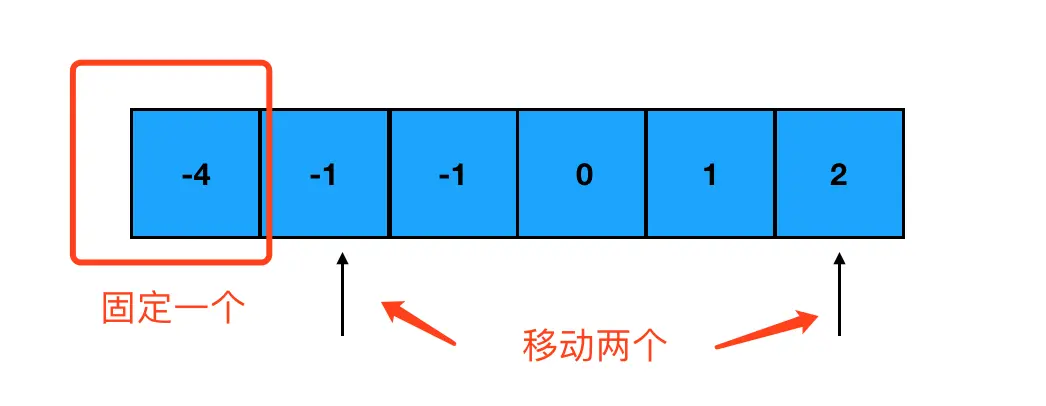每次指针移动一次位置，就计算一下两个指针指向数字之和加上固定的那个数之后，是否等于0。如果是，那么我们就得到了一个目标组合；否则，分两种情况来看：

• 相加之和大于0，说明右侧的数偏大了，右指针左移

• 相加之和小于0，说明左侧的数偏小了，左指针右移

tips：这个数组在题目中要求了"不重复的三元组"，因此我们还需要做一个重复元素的跳过处理。这一点在编码实现环节大家会注意到。

编码实现

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
const threeSum = function(nums) {
    // 用于存放结果数组
    let res = [] 
    // 给 nums 排序
    nums = nums.sort((a,b)=>{
        return a-b
    })
    // 缓存数组长度
    const len = nums.length
    // 注意我们遍历到倒数第三个数就足够了，因为左右指针会遍历后面两个数
    for(let i=0;i<len-2;i++) {
        // 左指针 j
        let j=i+1 
        // 右指针k
        let k=len-1   
        // 如果遇到重复的数字，则跳过
        if(i>0&&nums[i]===nums[i-1]) {
            continue
        }
        while(j<k) {
            // 三数之和小于0，左指针前进
            if(nums[i]+nums[j]+nums[k]<0){
                j++
               // 处理左指针元素重复的情况
               while(j<k&&nums[j]===nums[j-1]) {
                    j++
                }
            } else if(nums[i]+nums[j]+nums[k]>0){
                // 三数之和大于0，右指针后退
                k--
               
               // 处理右指针元素重复的情况
               while(j<k&&nums[k]===nums[k+1]) {
                    k--
                }
            } else {
                // 得到目标数字组合，推入结果数组
                res.push([nums[i],nums[j],nums[k]])
                
                // 左右指针一起前进
                j++  
                k--
               
                // 若左指针元素重复，跳过
                while(j<k&&nums[j]===nums[j-1]) {
                    j++
                }  
               
               // 若右指针元素重复，跳过
               while(j<k&&nums[k]===nums[k+1]) {
                    k--
                }
            }
        }
    }
    
    // 返回结果数组
    return res
};

双指针法中的"对撞指针"法

在上面这道题中，左右指针一起从两边往中间位置相互迫近，这样的特殊双指针形态，被称为"对撞指针"。

什么时候你需要联想到对撞指针？

这里我给大家两个关键字------"有序"和"数组"。

没错，见到这两个关键字，立刻把双指针法调度进你的大脑内存。普通双指针走不通，立刻想对撞指针！

即便数组题目中并没有直接给出"有序"这个关键条件，我们在发觉普通思路走不下去的时候，也应该及时地尝试手动对其进行排序试试看有没有新的切入点------没有条件，创造条件也要上。

对撞指针可以帮助我们缩小问题的范围，这一点在"三数求和"问题中体现得淋漓尽致：因为数组有序，所以我们可以用两个指针"画地为牢"圈出一个范围，这个范围以外的值不是太大就是太小、直接被排除在我们的判断逻辑之外，这样我们就可以把时间花在真正有意义的计算和对比上。如此一来，不仅节省了计算的时间，更降低了问题本身的复杂度，我们做题的速度也会大大加快。

（阅读过程中有任何想法或疑问，或者单纯希望和笔者交个朋友啥的，欢迎大家添加我的微信xyalinode与我交流哈~） 字符串在算法面试中，单独考察的机会并不多，同样倾向于和一些经典算法（后面会讲的）结合来体现区分度。步子不能跨太大，不然容易扯着x。本节我们照样是先解决只需要数据结构知识做基础就可以解决的字符串问题。

在讲题之前，我首先要给大家点拨两个字符串相关的"基本算法技能"。这两个技能偶尔也会单独命题，但整体来看在综合性题目中的考察频率较高，需要大家着重熟悉、反复练习和记忆，确保真正做题时万无一失。

基本算法技能

反转字符串

在 JS 中，反转字符串我们直接调相关 API 即可，相信不少同学都能手到擒来：

// 定义被反转的字符串 
const str = 'juejin'  
// 定义反转后的字符串
const res = str.split('').reverse().join('')

console.log(res) // nijeuj

（这段代码需要你非常熟悉，一些公司一面为了试水，有时会单独考这个操作）。

判断一个字符串是否是回文字符串

回文字符串，就是正着读和倒着读都一🐱一样的字符串，比如这样的：

'yessey'

结合这个定义，我们不难写出一个判定回文字符串的方法：

function isPalindrome(str) {
    // 先反转字符串
    const reversedStr = str.split('').reverse().join('')
    // 判断反转前后是否相等
    return reversedStr === str
}

同时，回文字符串还有另一个特性：如果从中间位置"劈开"，那么两边的两个子串在内容上是完全对称的。因此我们也可以结合对称性来做判断：

function isPalindrome(str) {
    // 缓存字符串的长度
    const len = str.length
    // 遍历前半部分，判断和后半部分是否对称
    for(let i=0;i<len/2;i++) {
        if(str[i]!==str[len-i-1]) {
            return false
        }
    }
    return true
}

（谨记这个对称的特性，非常容易用到）

高频真题解读

回文字符串的衍生问题

真题描述：给定一个非空字符串 s，最多删除一个字符。判断是否能成为回文字符串。
示例 1: 输入: "aba"

输出: True

示例 2:

输入: "abca"

输出: True

解释: 你可以删除c字符。

注意: 字符串只包含从 a-z 的小写字母。字符串的最大长度是50000。

思路分析

这道题很多同学第一眼看过去，可能本能地会想到这样一种解法：若字符串本身不回文，则直接遍历整个字符串。遍历到哪个字符就删除哪个字符、同时对删除该字符后的字符串进行是否回文的判断，看看存不存在删掉某个字符后、字符串能够满足回文的这种情况。

这个思路真的实现起来的话，在判题系统眼里其实也是没啥毛病的。但是在面试官看来，就有点问题了------这不是一个高效的解法。

如何判断自己解决回文类问题的解法是否"高效"？其中一个很重要的标准，就是看你对回文字符串的对称特性利用得是否彻底。

字符串题干中若有"回文"关键字，那么做题时脑海中一定要冒出两个关键字------对称性 和 双指针。这两个工具一起上，足以解决大部分的回文字符串衍生问题。

回到这道题上来，我们首先是初始化两个指针，一个指向字符串头部，另一个指向尾部：

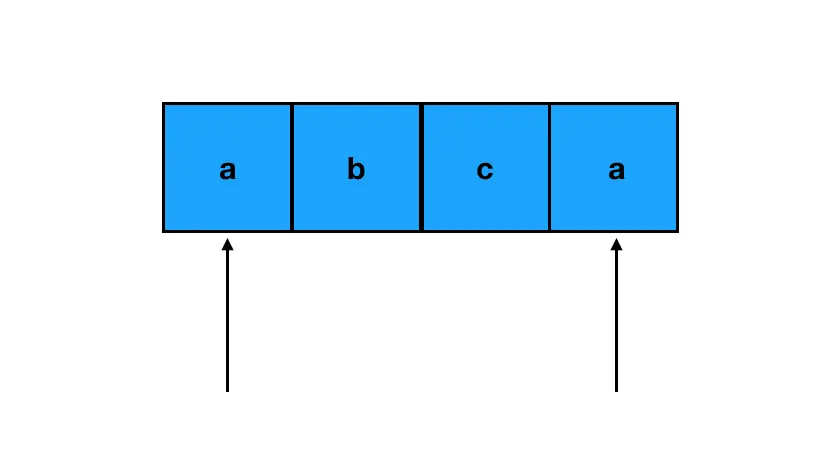
如果两个指针所指的字符恰好相等，那么这两个字符就符合了回文字符串对对称性的要求，跳过它们往下走即可。如果两个指针所指的字符串不等，比如这样：

那么就意味着不对称发生了，意味着这是一个可以"删掉试试看"的操作点。我们可以分别对左指针字符和右指针字符尝试进行"跳过"，看看区间在 [left+1, right] 或 [left, right-1] 的字符串是否回文。如果是的话，那么就意味着如果删掉被"跳过"那个字符，整个字符串都将回文：

比如说这里我们跳过了 b，[left+1, right] 的区间就是 [2, 2]，它对应 c 这个字符，单个字符一定回文。这样一来，删掉 b 之后，左右指针所指的内部区间是回文的，外部区间也是回文的，可以认为整个字符串就是一个回文字符串了。

编码实现

const validPalindrome = function(s) {
    // 缓存字符串的长度
    const len = s.length

    // i、j分别为左右指针
    let i=0, j=len-1
    
    // 当左右指针均满足对称时，一起向中间前进
    while(i<j&&s[i]===s[j]) {
        i++ 
        j--
    }
    
    // 尝试判断跳过左指针元素后字符串是否回文
    if(isPalindrome(i+1,j)) {
      return true
    }
    // 尝试判断跳过右指针元素后字符串是否回文
    if(isPalindrome(i,j-1)) {
        return true
    }
    
    // 工具方法，用于判断字符串是否回文
    function isPalindrome(st, ed) {
        while(st<ed) {
            if(s[st] !== s[ed]) {
                return false
            }
            st++
            ed--
        } 
        return true
    }
    
    // 默认返回 false
    return false 
};

字符串匹配问题------正则表达式初相见

接下来我们来看一道综合性比较强的字符串大题：

真题描述： 设计一个支持以下两种操作的数据结构：

void addWord(word)

bool search(word)

search(word) 可以搜索文字或正则表达式字符串，字符串只包含字母 . 或 a-z 。

. 可以表示任何一个字母。
示例: addWord("bad")

addWord("dad")

addWord("mad")

search("pad") -> false

search("bad") -> true

search(".ad") -> true

search("b..") -> true

说明:

你可以假设所有单词都是由小写字母 a-z 组成的。

思路分析

这道题要求字符串既可以被添加、又可以被搜索，这就意味着字符串在添加时一定要被存在某处。键值对存储，我们用 Map（或对象字面量来模拟 Map）。

注意，这里为了降低查找时的复杂度，我们可以考虑以字符串的长度为 key，相同长度的字符串存在一个数组中，这样可以提高我们后续定位的效率。

难点在于 search 这个 API，它既可以搜索文字，又可以搜索正则表达式。因此我们在搜索前需要额外判断一下，传入的到底是普通字符串，还是正则表达式。若是普通字符串，则直接去 Map 中查找是否有这个 key；若是正则表达式，则创建一个正则表达式对象，判断 Map 中相同长度的字符串里，是否存在一个能够与这个正则相匹配。

这里需要大家复习一下正则表达式的创建，以及用于测试某个字符串是否与之匹配的方法：

/**
 * 构造函数
 */
const WordDictionary = function () {
  // 初始化一个对象字面量，承担 Map 的角色
  this.words = {}
};

/**
  添加字符串的方法
 */
WordDictionary.prototype.addWord = function (word) {
  // 若该字符串对应长度的数组已经存在，则只做添加
  if (this.words[word.length]) {
    this.words[word.length].push(word)
  } else {
    // 若该字符串对应长度的数组还不存在，则先创建
    this.words[word.length] = [word]
  }

};

/**
  搜索方法
 */
WordDictionary.prototype.search = function (word) {
  // 若该字符串长度在 Map 中对应的数组根本不存在，则可判断该字符串不存在
  if (!this.words[word.length]) {
    return false
  }
  // 缓存目标字符串的长度
  const len = word.length
  // 如果字符串中不包含'.'，那么一定是普通字符串
  if (!word.includes('.')) {
    // 定位到和目标字符串长度一致的字符串数组，在其中查找是否存在该字符串
    return this.words[len].includes(word)

  }

  // 否则是正则表达式，要先创建正则表达式对象
  const reg = new RegExp(word)

  // 只要数组中有一个匹配正则表达式的字符串，就返回true
  return this.words[len].some((item) => {
    return reg.test(item)
  })
};

正则表达式更进一步------字符串与数字之间的转换问题

真题描述：请你来实现一个 atoi 函数，使其能将字符串转换成整数。

首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。

当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号；假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成整数。

该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响。

注意：假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换。

在任何情况下，若函数不能进行有效的转换时，请返回 0。
说明： 假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−2^31, 2^31 − 1]。如果数值超过这个范围，请返回 INT_MAX (2^31 − 1) 或 INT_MIN (−2^31) 。
示例 1:

输入: "42"

输出: 42
示例 2:

输入: " -42"

输出: -42

解释: 第一个非空白字符为 '-', 它是一个负号。

我们尽可能将负号与后面所有连续出现的数字组合起来，最后得到 -42 。
示例 3: 输入: "4193 with words"

输出: 4193

解释: 转换截止于数字 '3' ，因为它的下一个字符不为数字。
示例 4: 输入: "words and 987"

输出: 0

解释: 第一个非空字符是 'w', 但它不是数字或正、负号。 因此无法执行有效的转换。
示例 5:

输入: "-91283472332"

输出: -2147483648

解释: 数字 "-91283472332" 超过 32 位有符号整数范围。因此返回 INT_MIN (−2^31) 。

思路解读

这道题乍一看比较唬人，毕竟题干这么长，首先会刷掉一波没耐心读完的火大老哥。我在实际的面试情景下，见过题没读完就掀桌走人的.....嗨，这里特别提醒大家，千万别冲动：小孩子才害怕读题，成年人都偷着乐------你得知道，一般来说，题干越长，题目越好做。

为啥这样说？大家想想，我们做题靠的是什么？自身的知识储备+题目提供的信息。题干长意味着什么？意味着它提供的信息相对丰富、细节描述相对到位，甚至很有可能，这个题的答案都藏在题里了！

就拿这道题开刀，我把其中比较关键的句子摘出来给大家翻译翻译：

1. 该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止------暗示你拿到字符串先去空格；

2. 当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号------暗示你识别开头的"+"字符和"-"字符；

3. 该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响------暗示你见到非整数字符就刹车；

4. 说明： 假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−2^31, 2^31 − 1]。如果数值超过这个范围，请返回 INT_MAX (2^31 − 1) 或 INT_MIN (−2^31) ------暗示......这都不是暗示了，这是明示啊！直接告诉你先把这俩边界值算出来，摆在那做卡口就完了。

Step1：计算卡口

所以说不管这道题你用啥方法做，这个卡口计算肯定是没跑了。计算某个数的 n 次方，我们要用到 Math.pow 这个方法：

// 计算最大值
const max = Math.pow(2,31) - 1
// 计算最小值
const min = -max - 1

Step2：解析字符串

这道题其实有很多种解法，不同解法之间的区别就在于解析字符串的方式不同。

最直接的解法，是对字符串进行遍历，在遍历的过程中，按照上文我给大家提取的 1、2、3 这三点暗示，逐个地去对每个遍历对象进行判断，从而提取出符合题目要求的数字字符串，再把它转换成数字。

这样做理论上来说没毛病，也不会有超时问题。不过这里我更推荐大家用正则来做，原因很简单：我们看题目里有这么密集的字符串约束条件，作为前端，本能地是能想到用正则来做的；同时，正则表达式本身就是前端面试中的一个基础知识点，如果一道题能够同时考察字符串操作和正则表达式，其实也正中了面试官的下怀。

现在我们决定了用正则来做这道题，能不能做对它，就要看咱们正则表达式能不能写对了。

对于正则表达式，大多数的团队不会有特别强硬的要求，不会期望你一定要多么多么精通、能不靠 Google 徒手写多么复杂的表达式出来啥的------这样搞其实也没有意义。但是必要的基础你是要有的，这道题目涉及到的正则其实就在这个"必要"的范围里，我们一起来分析一下，首先是看回这三个约束条件，我重新给大家翻译一下：

1. 该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止------允许字符串头部出现空格，但是你在处理的时候要想办法把它摘出去，不要让它干扰你的计算

2. 当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号------允许字符串的第一个有效字符为"+"或者"---"，不要摘它出去，它对你的计算是有意义的

3. 该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响------匹配的时候，连续整数之外的部分都应该被摘除

通过以上分析，我们可以形成以下思路：

首先，摘除空格：有两个方法，一个是直接使用 string 的 trim 方法，它是 JavaScript 的一个原生方法，可以去除字符串的头尾空格:

let str = '      +10086'
str.trim() // '+10086'

另一个方法是在匹配的时候，匹配空格（正则匹配符为 \s*，意味着匹配 0 个或多个空格），但是不把它放在捕获组里------这种方法会更加通用，正则表达式匹配过程中，所有的"摘除"动作都可以通过将匹配到的结果排除在捕获组之外来实现，

什么是捕获组？其实就是正则表达式中被小括号括住的部分。在这道题里，我们需要从字符串中提取的其实只有"+/-"符号以及其后面的数字而已，同时这个字符串需要满足 可能存在的空格+正负号+数字字符串+其它字符内容 这样的格式才算合法，那我们就可以通过这样写正则表达式，实现"匹配"和"提取"的双重目的：

/\s*([-\+]?[0-9]*).*/

针对正则基础比较薄弱的同学，我来解释一下上面这个正则表达式：

• 首先，\s 这个符号，意味着空字符，它可以用来匹配回车、空格、换行等空白区域，这里，它用来被匹配空格。*这个符号，跟在其它符号后面，意味着"前面这个符号可以出现0次或多次。\s*，这里的意思就是空格出现0次或多次，都可被匹配到。
• 接着 () 出现了。() 圈住的内容，就是我们要捕获起来额外存储的东西。
• []中的匹配符之间是"或"的关系，也就是说只要能匹配上其中一个就行了。这里[]中包括了-和\+，-不必说匹配的是对应字符，这个\+之所以加了一个斜杠符，是因为+本身是一个有特殊作用的正则匹配符，这里我们要让它回归+字符的本义，所以要用一个\来完成转义。
• [0-9]*结合咱们前面铺陈的知识，这个就不难理解了，它的意思是 0-9 之间的整数，能匹配到0个或多个就算匹配成功。
• 最后的 .这个是任意字符的意思，.*用于字符串尾部匹配非数字的任意字符。我们看到.*是被排除捕获组之外的，所以说这个东西其实也不会被额外存储，它被"摘除"了。

Step3：获取捕获结果

JS 的正则相关方法中， test()方法返回的是一个布尔值，单纯判断"是否匹配"。要想获取匹配的结果，我们需要调度match()方法：

const reg = /\s*([-\+]?[0-9]*).*/
const groups = str.match(reg)

match() 方法是一个在字符串中执行查找匹配的String方法，它返回一个数组，在未匹配到时会返回 null。

如果我们的正则表达式尾部有 g 标志，match()会返回与完整正则表达式匹配的所有结果，但不会返回捕获组。

这里我们没有使用g标志，match()就会返回第一个完整匹配（作为数组的第0项）及其相关的捕获组（作为数组的第1及第1+项）。

这里我们只定义了一个捕获组，因此可以从 groups[1] 里拿到我们捕获的结果。

Step4：判断卡口 最后一步，就是把捕获的结果转换成数字，看看是否超出了题目要求的范围。这一步比较简单，无需多言。

编码实现

分析了这么多，我们终于可以写代码啦：

// 入参是一个字符串
const myAtoi = function(str) {
    // 编写正则表达式
    const reg = /\s*([-\+]?[0-9]*).*/
    // 得到捕获组
    const groups = str.match(reg)
    // 计算最大值
    const max = Math.pow(2,31) - 1
    // 计算最小值
    const min = -max - 1
    // targetNum 用于存储转化出来的数字
    let targetNum = 0
    // 如果匹配成功
    if(groups) {
        // 尝试转化捕获到的结构
        targetNum = +groups[1]
        // 注意，即便成功，也可能出现非数字的情况，比如单一个'+'
        if(isNaN(targetNum)) {
            // 不能进行有效的转换时，请返回 0
            targetNum = 0
        }
    }
    // 卡口判断
    if(targetNum > max) {
        return max
    } else if( targetNum < min) {
        return min
    }
    // 返回转换结果
    return targetNum
};

冲！