预测算法一:灰色预测模型 灰色预测是对含有已知信息又含有不确定信息的系统进行预测,就是对一定范围内变化的、与时间有关的灰色过程进行预测; 注:1、提供灰色预测相关论文已经学习资料,提供数学建模指导 2、Matlab代码
在数据科学和预测分析的世界里,灰色预测模型(Grey Prediction Model)是一种独特而强大的工具,尤其适用于那些数据不完全或信息不明确的系统。今天,我们就来深入探讨一下这个模型,并通过一些实际的Matlab代码来加深理解。
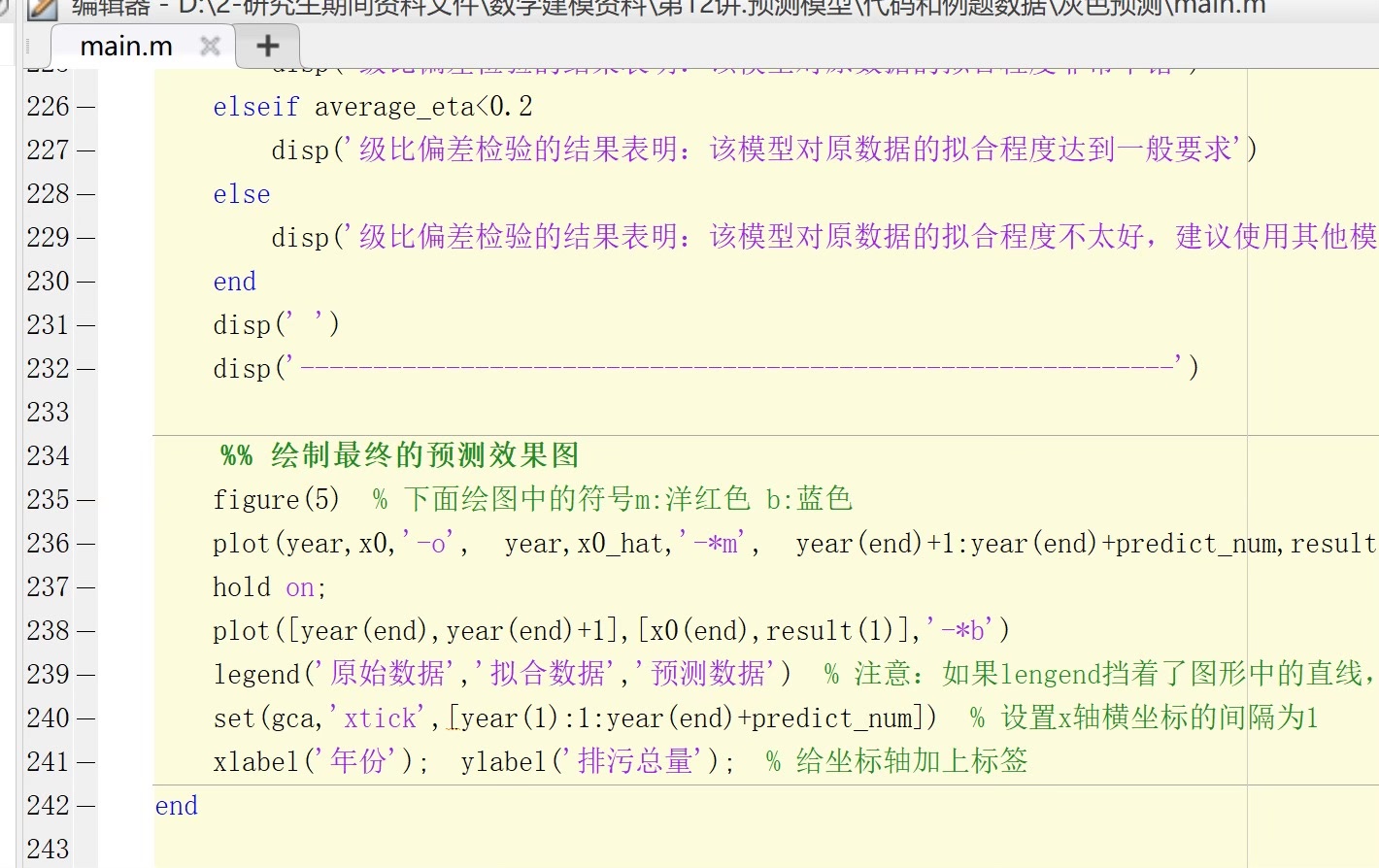
首先,灰色预测模型的核心思想是基于"灰色系统理论",这种理论认为,尽管某些系统信息不完全,我们仍然可以通过已知的部分信息来预测未来的趋势。这听起来有点像在黑暗中摸索,但别担心,数学和代码会给我们指明方向。
让我们从一个简单的例子开始。假设我们有一组时间序列数据,表示某产品的月销售额。我们的目标是预测下个月的销售额。首先,我们需要对数据进行一些预处理,比如累加生成序列(AGO),这是灰色预测中的一个关键步骤。
matlab
% 原始数据
original_data = [120, 140, 160, 180, 200];
% 累加生成序列
ago_data = cumsum(original_data);在这个代码片段中,cumsum函数用于计算数据的累加和。累加生成序列是灰色预测模型的基础,它帮助我们减少数据的随机性,使得预测更加稳定。
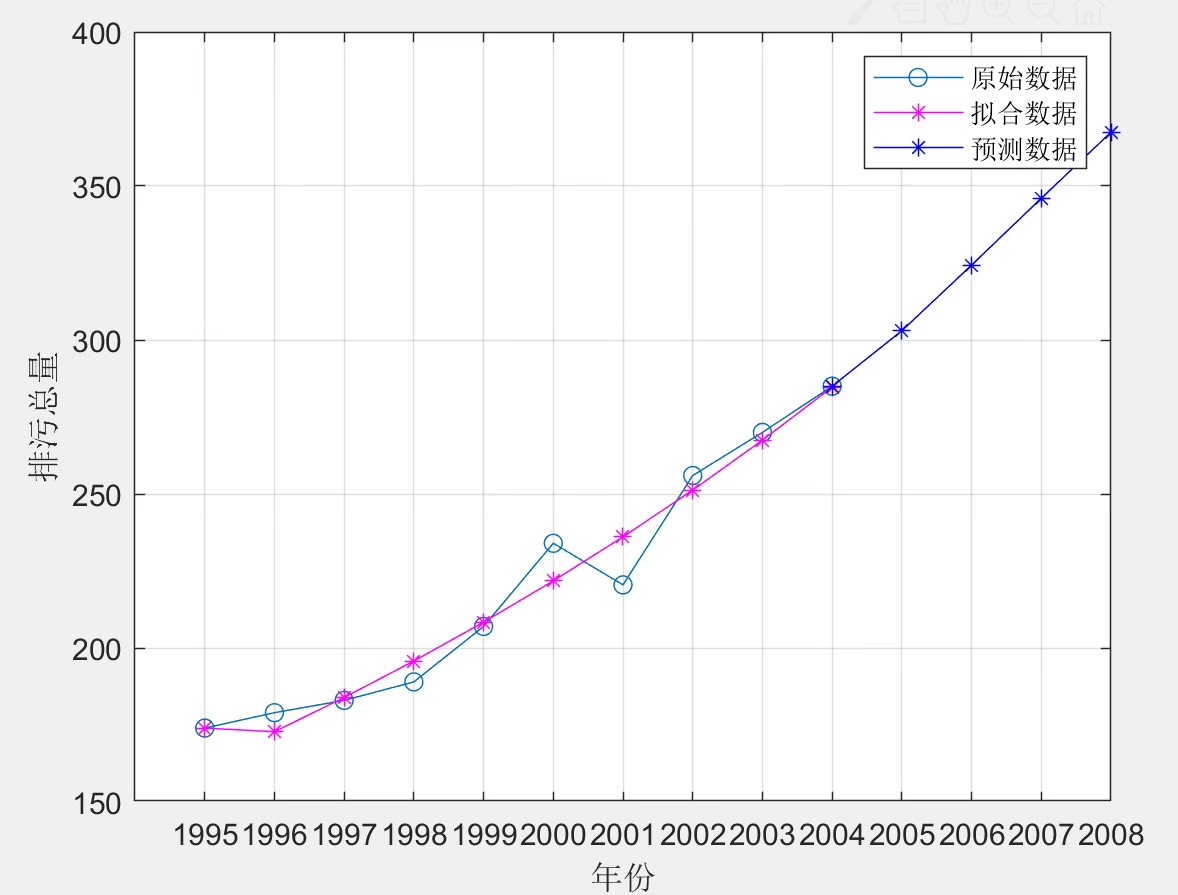
接下来,我们需要建立灰色微分方程,这是模型的核心部分。灰色微分方程通常表示为:
\[ \frac{dx^{(1)}}{dt} + ax^{(1)} = b \]
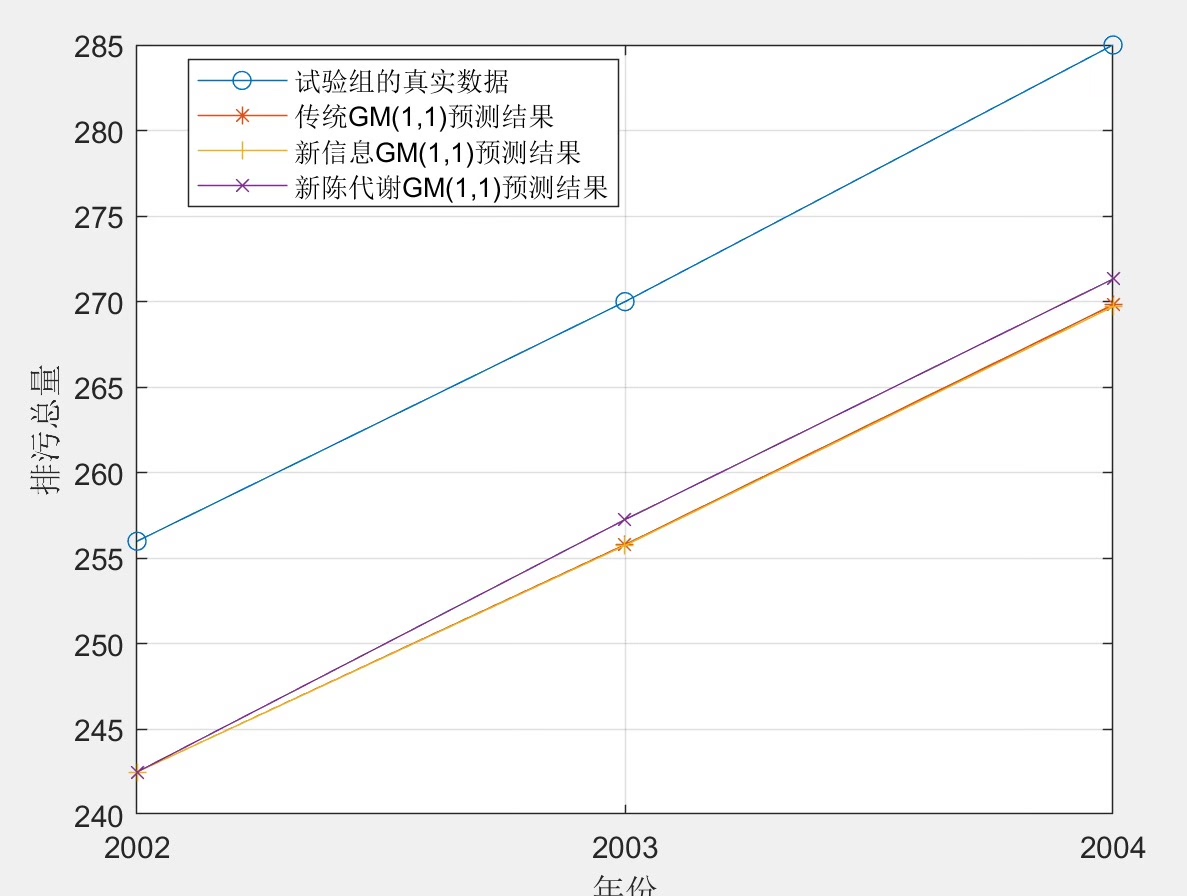
其中,\( x^{(1)} \) 是累加生成序列,\( a \) 和 \( b \) 是待估计的参数。在Matlab中,我们可以使用最小二乘法来估计这些参数。
matlab
% 构造矩阵B和Y
B = [-ago_data(1:end-1)', ones(length(ago_data)-1, 1)];
Y = original_data(2:end)';
% 估计参数a和b
params = B \ Y;
a = params(1);
b = params(2);在这个代码中,我们构造了矩阵B和Y,然后使用最小二乘法来估计参数a和b。这些参数将用于后续的预测。
有了参数,我们就可以进行预测了。灰色预测模型的预测公式为:
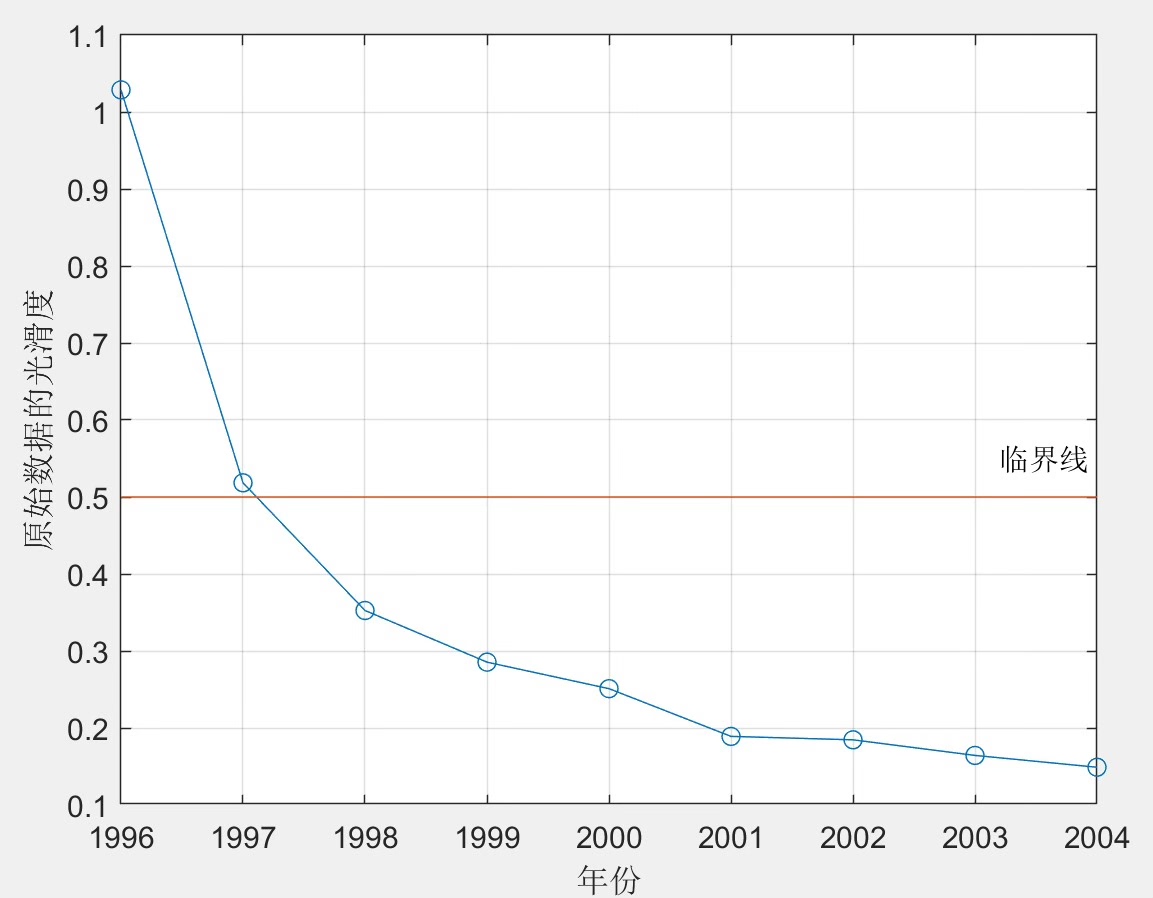
\[ \hat{x}^{(1)}(k+1) = \left( x^{(1)}(1) - \frac{b}{a} \right) e^{-a k} + \frac{b}{a} \]
在Matlab中,我们可以实现这个公式来进行预测:
matlab
% 预测值
k = length(original_data);
predicted_value = (ago_data(1) - b/a) * exp(-a * k) + b/a;
% 还原到原始数据
predicted_original_value = predicted_value - ago_data(end-1);最后,我们得到了预测的下个月销售额。当然,这只是一个简单的例子,实际应用中可能需要更复杂的处理和更多的数据。
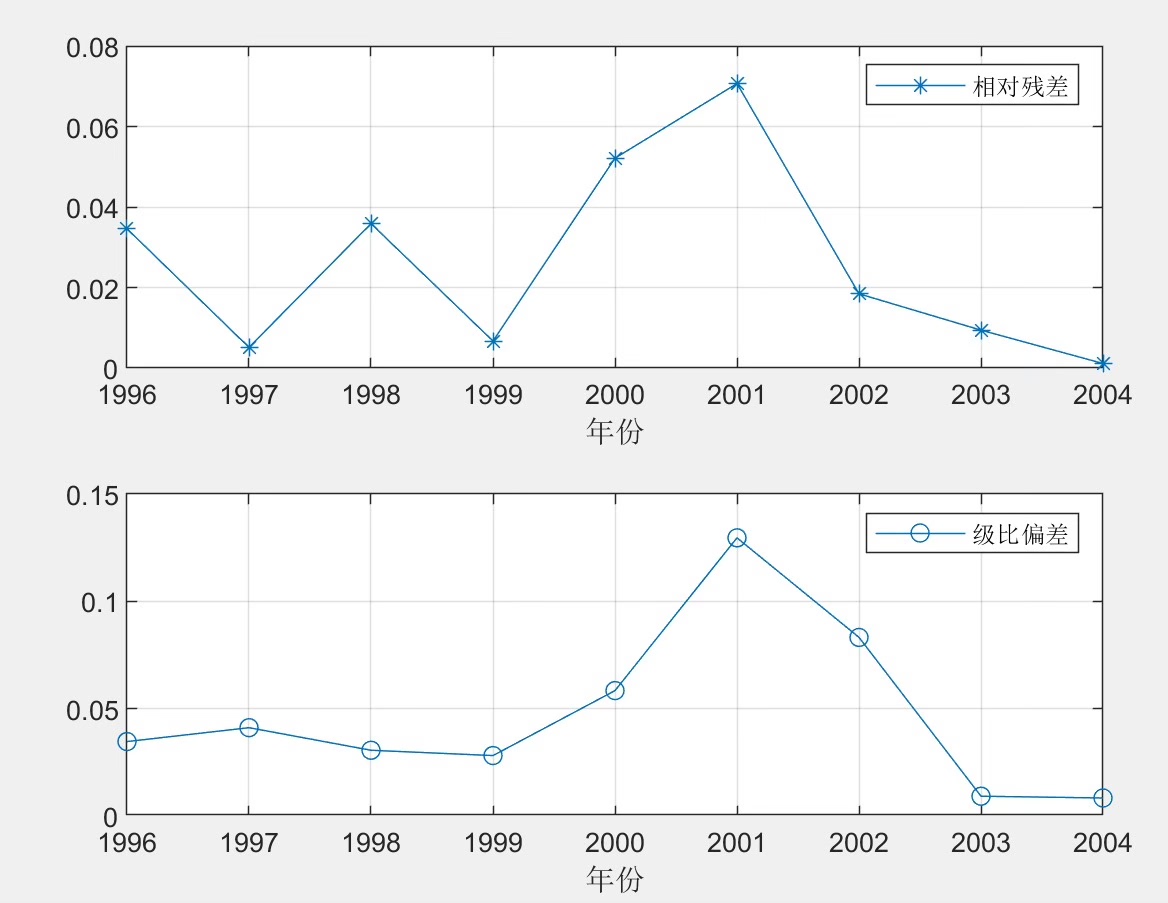
灰色预测模型的一个优点是它不需要大量的历史数据,即使只有几个数据点,也能进行有效的预测。这使得它在许多实际应用中非常有用,特别是在数据稀缺或不确定的情况下。
总的来说,灰色预测模型是一种灵活且强大的预测工具,通过Matlab的实现,我们可以轻松地将其应用于各种实际问题。希望这篇文章和代码示例能帮助你更好地理解和使用灰色预测模型。如果你有任何问题或需要进一步的帮助,随时可以查阅相关论文或寻求数学建模的指导。