基于Stacking集成学习算法的数据回归预测（基学习器PLS和SVM，元学习器RF），MATLAB代码

基于Stacking集成学习算法的数据回归预测（基学习器PLS和SVM，元学习器RF），MATLAB代码

---

一、研究背景

该研究属于机器学习集成学习领域，针对单一回归模型可能存在的预测偏差或过拟合问题，采用Stacking集成方法，结合不同基学习器的优势，提升回归预测的稳定性。适用于需要预测的复杂数据场景。

---

二、主要功能

1. 使用Stacking集成学习框架进行数据回归预测。
2. 基学习器包括：
   • 偏最小二乘回归（PLS）
   • 支持向量机回归（SVR），带网格搜索调参
3. 元学习器采用随机森林回归（RF）。
4. 包含完整的数据预处理、模型训练、性能评估与可视化流程。

---

三、算法步骤

1. 数据准备：读取数据、归一化、划分训练集与测试集（7:3）。
2. 基学习器训练 ：
   • PLS：通过交叉验证选择最佳成分数。
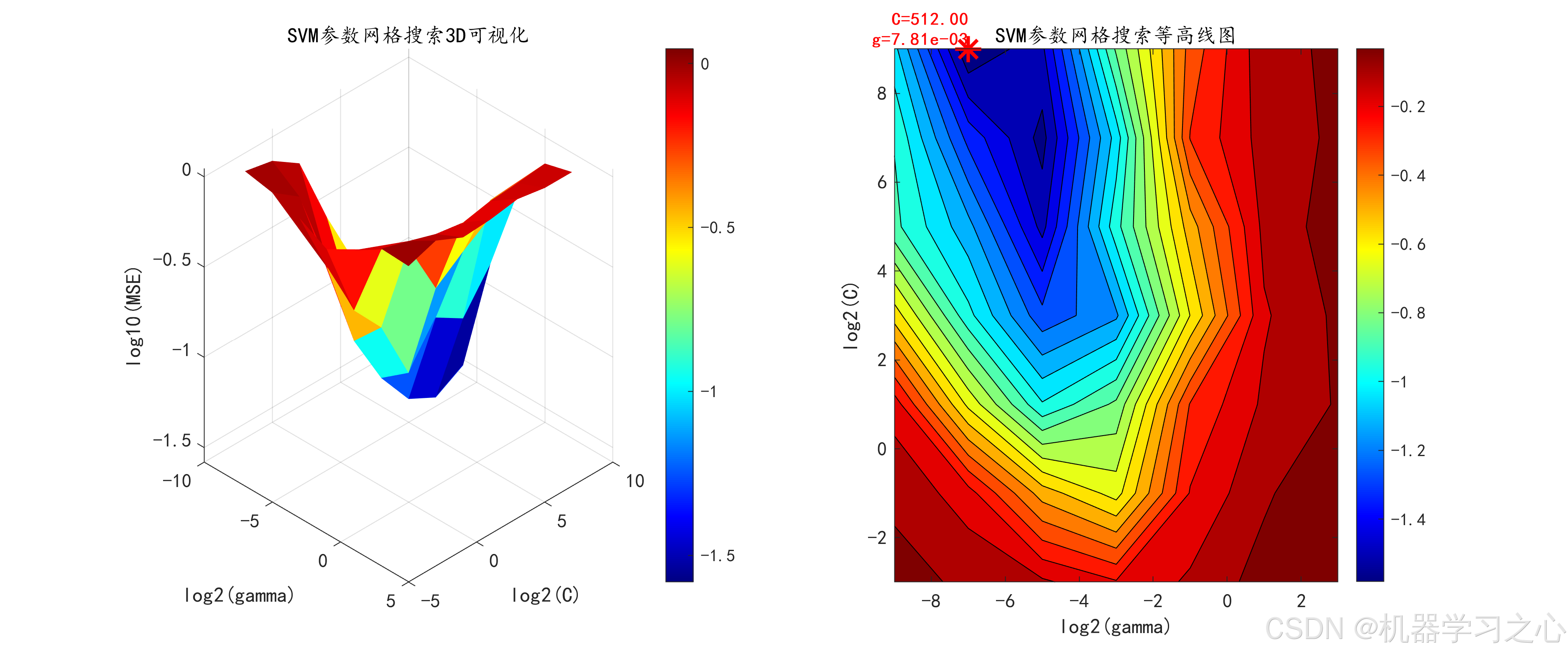
   • SVM：网格搜索优化C和gamma参数，并绘制3D可视化图。
3. 元特征构建：使用基学习器的预测结果作为新特征。
4. 元学习器训练：使用随机森林对元特征进行回归。
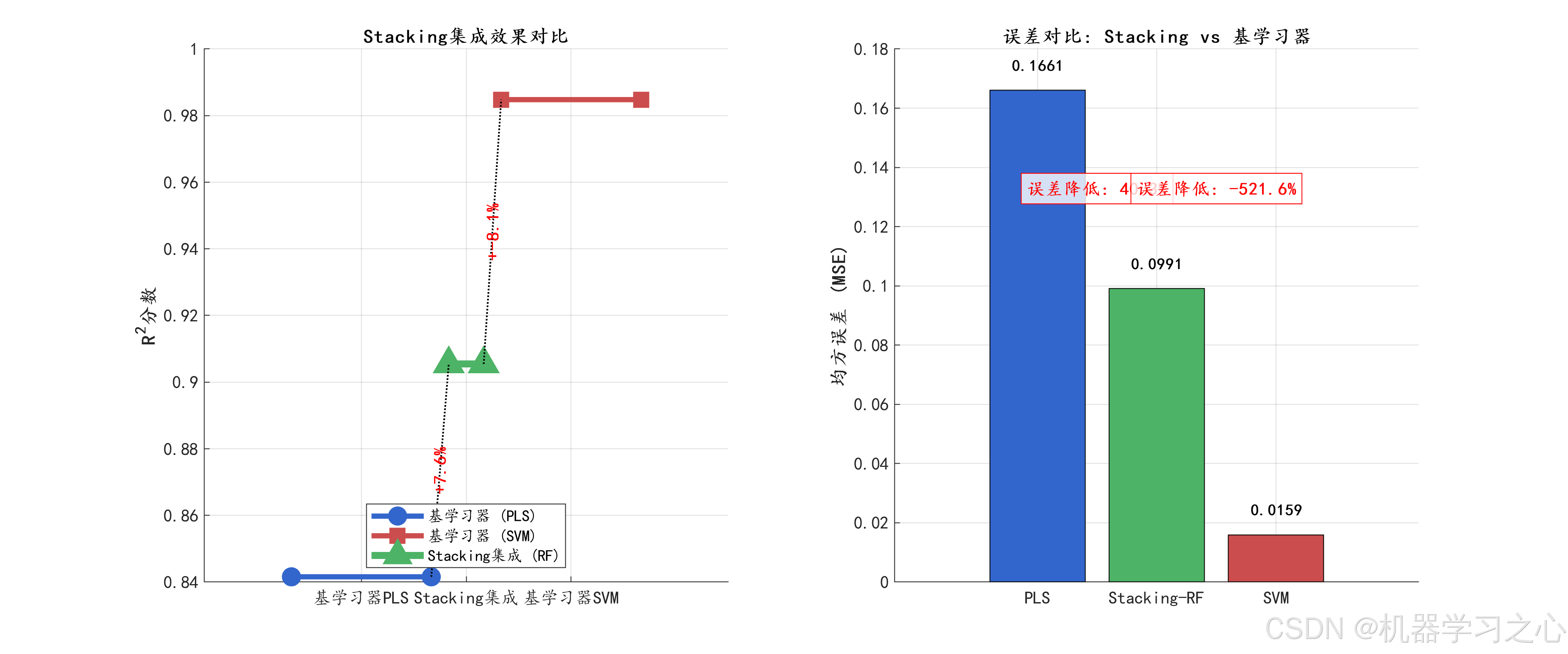
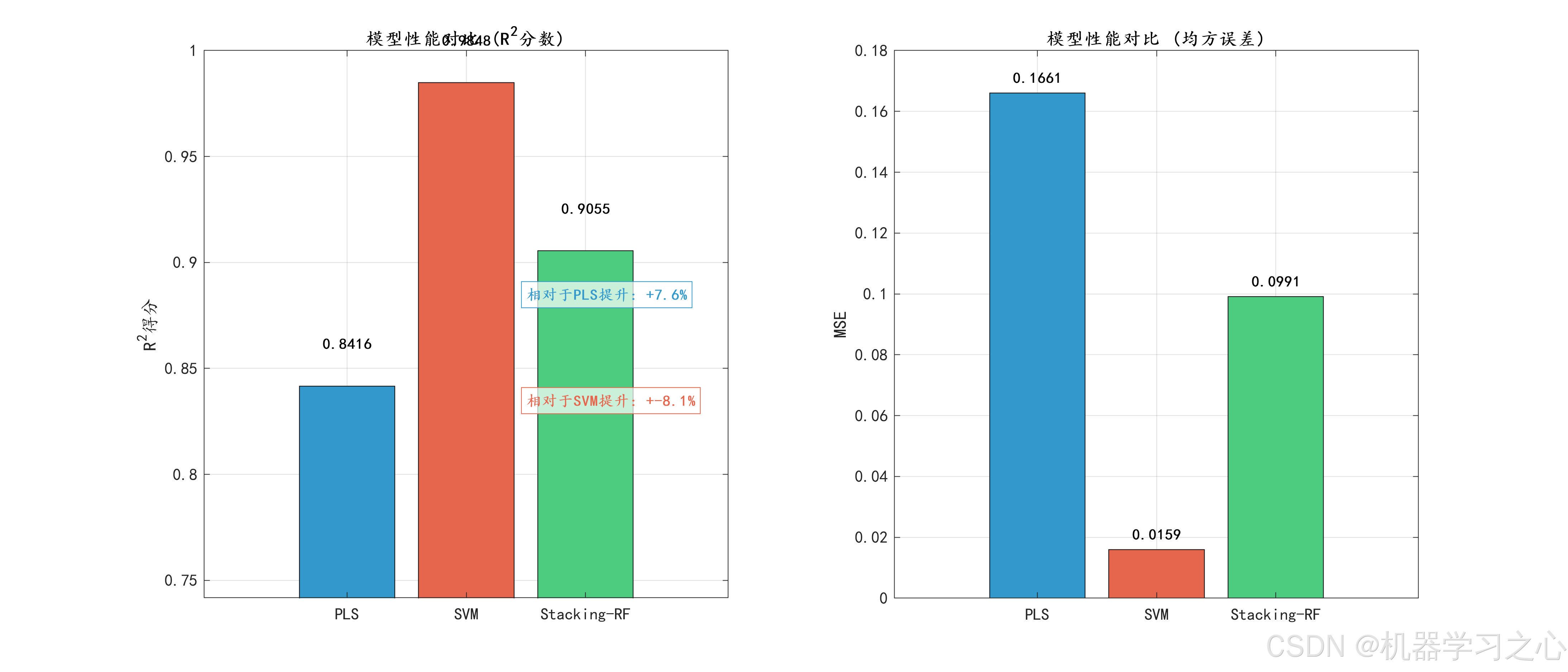
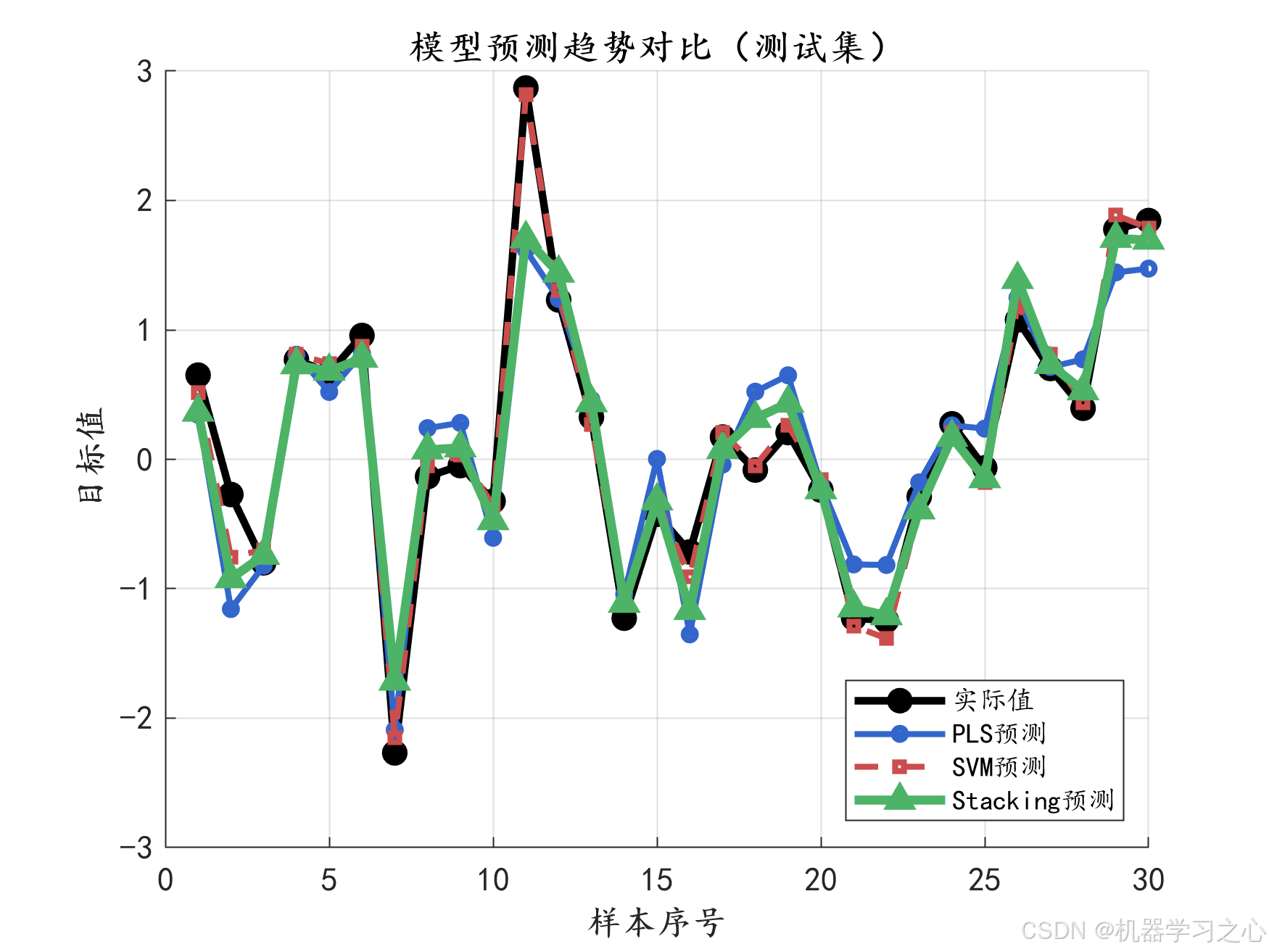
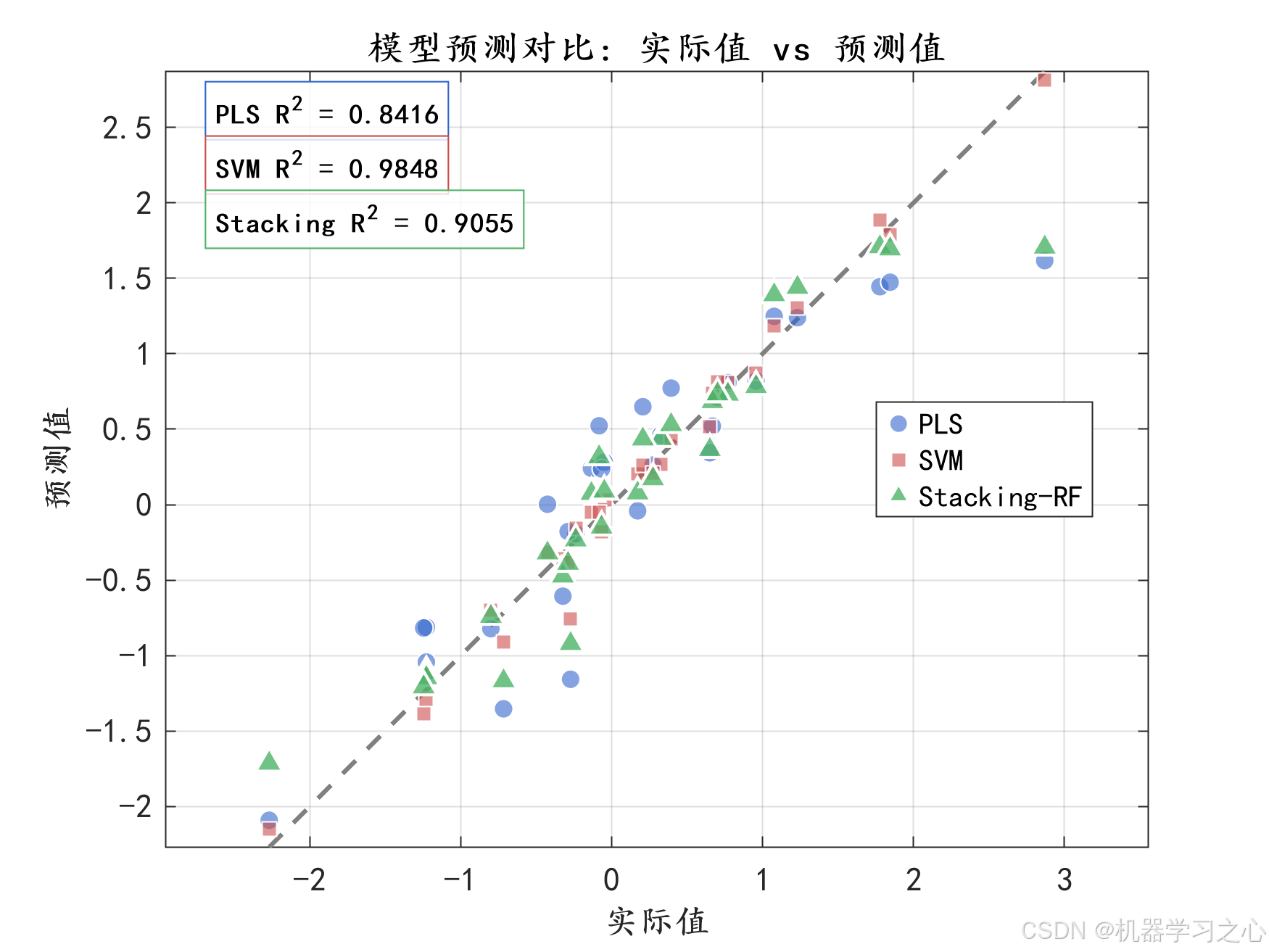
5. 模型评估：对比PLS、SVM和Stacking-RF在训练集和测试集上的性能。
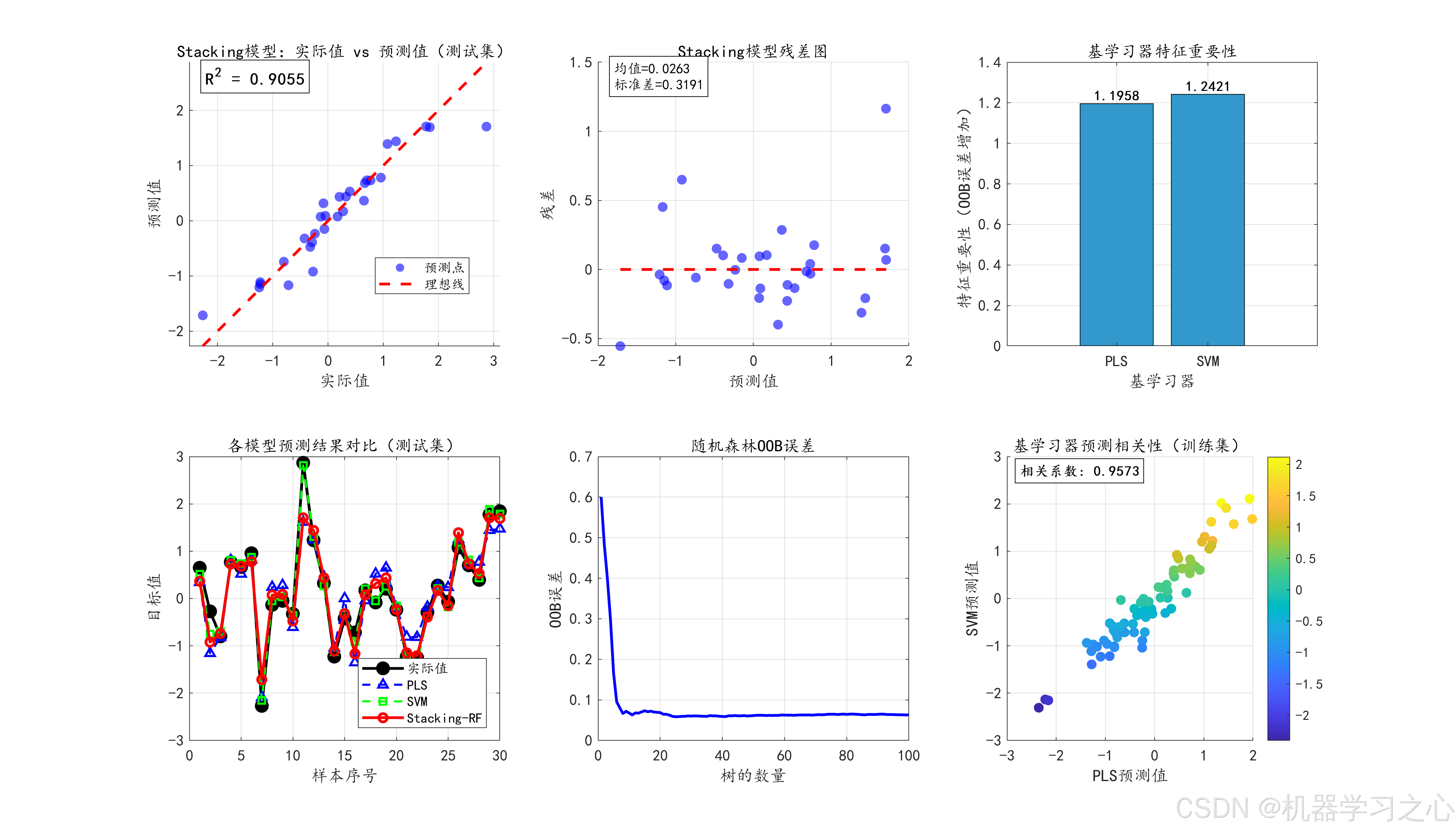
6. 可视化分析：包括预测图、残差图、特征重要性、OOB误差、模型对比等。

---

四、技术路线

原始数据 → 归一化 → 划分数据集 → 训练PLS → 训练SVM（调参） → 构建元特征 → 训练随机森林 → 预测与评估 → 可视化输出

---

五、公式原理

• PLS：通过提取自变量与因变量的潜在变量，最大化协方差进行回归。
• SVM（RBF核）：通过核函数将数据映射到高维空间，寻找最优回归超平面。
• 随机森林：通过构建多棵决策树并集成其预测结果，减少过拟合。
• Stacking ：
  y^stack=fmeta(h1(X),h2(X)) \hat{y}{stack} = f{meta}(h_1(X), h_2(X)) y^stack=fmeta(h1(X),h2(X))
  其中 h1,h2h_1, h_2h1,h2 为基学习器，fmetaf_{meta}fmeta 为元学习器。

---

六、参数设定

模型	参数	设定值/范围
PLS	最大成分数	20（动态选择最佳）
SVM	C参数范围	(2^{-3} \sim 2^9)
SVM	gamma参数范围	(2^{-9} \sim 2^3)
RF	树的数量	100
RF	最小叶子节点数	5

---

七、运行环境

• 平台：MATLAB
• 依赖工具箱：Statistics and Machine Learning Toolbox
• 数据格式：Excel文件，最后一列为目标变量
• 内存要求：建议8GB以上，尤其处理大规模网格搜索时

---

八、应用场景

• 复杂数据的回归预测问题，如：
  • 金融数据预测
  • 工业过程建模
  • 生物医学数据分析
  • 环境监测与预测
  • 销售与需求预测
• 适用于中小规模数据集，支持特征数量适中、样本量在几千以内的回归任务。

完整代码私信回复基于Stacking集成学习算法的数据回归预测（基学习器PLS和SVM，元学习器RF），MATLAB代码