分级存储体系

1.分级存储体系

你总结得非常到位，也抓住了分级存储体系的核心思想。

您提到的 "容量、成本和速度之间的矛盾" 是计算机存储系统设计的根本性难题，而 分级存储体系 就是解决这个"不可能三角"的经典方案。

让我对您的总结进行一些扩展和补充，使其更完整：

1.1 核心矛盾（不可能三角）

不可能三角：指的是在三个理想的目标或属性中，最多只能同时实现其中两个，而无法三者兼得。它描述了一种根本性的权衡关系，强调资源、约束或物理定律的限制。其经典表达形式是一个三角形，每个顶点代表一个理想属性，但你必须至少放弃其中一个。

大容量
高速度（低延迟，高带宽）
低成本（每比特存储的价格低廉）

为什么"容量大"和"速度快"天生矛盾？

这主要受制于三个层面的根本约束：

物理定律层面：信号传播与寻址

速度要求物理接近：信号在介质中传播需要时间（光速是极限）。为了快，存储单元必须离CPU（计算核心）物理距离近，并且结构简单，这样才能在纳秒级响应。这就严重限制了能集成在近处的单元数量，导致容量做不大。

容量要求复杂结构：大容量意味着海量的存储单元。管理和访问这么多单元，需要复杂的地址译码电路和内部结构。每增加一层寻址和选择逻辑，就会引入额外的延迟。一个简单的比喻：从10个抽屉里找东西（小容量高速缓存），比从一万个抽屉的仓库里找东西（大容量内存）快得多，因为前者几乎一眼就能看到。

半导体技术层面：工艺与功耗

高速需要昂贵的工艺：像CPU缓存（SRAM）用的晶体管是6管结构，速度快但结构复杂、占面积大、功耗高。在同样大小的芯片上，你只能放很少的这种"高速单元"。

大容量需要高密度：像主存（DRAM）用的晶体管是1管1电容结构，非常紧凑，但速度慢且需要定期刷新。像硬盘（HDD）则完全抛弃了电路寻址，改用机械磁头，单位成本极低，但速度慢了百万倍。

功耗墙与散热：即使技术上能把海量的高速单元做在一起，其产生的巨大功耗和热量也无法散去。芯片会立刻烧毁。速度越快，单位操作耗能越大。大容量高速存储的功耗是灾难性的。

经济学层面：成本

高速介质成本高昂：前面提到的SRAM，其单位比特（bit）的成本是DRAM的数十倍，是SSD的数千倍，是HDD的数万倍。如果用SRAM来做1TB的"内存"，其价格将是天文数字，没有任何市场能承受。

市场定位与平衡：厂商会根据"速度-容量-成本"三角来设计不同产品线，满足不同需求，而不是去制造一个在三个方面都达到极致的"怪物"。

所以，在单一存储介质中，这三者无法同时达到最优：

SRAM（用作Cache）：极快，但容量小、成本极高。
DRAM（主存）：速度较快，容量较大，成本适中，但断电数据丢失。
硬盘/SSD（辅存）：容量极大，成本极低（每比特），但速度很慢（相比内存）。

简单类比：

想象一个图书馆。

高速缓存（SRAM）就像你手边的桌面：面积很小（容量小），只能放几本最常看的书，但拿起来（访问）极快。维护这个桌面（成本）很贵，因为你占用了宝贵的办公空间。
主存（DRAM）像你办公室的书架：比桌面大得多（容量较大），找书也较快，但需要你站起来走过去。
辅存（硬盘）像城市里的巨型图书馆：容量巨大，找一本书需要查目录、走路、甚至申请调阅，速度非常慢，但每本书的存储成本极低。

还有一个经济例子，由经济学家罗伯特·蒙代尔提出，描述了货币政策的三个目标：

三个顶点是：
- 资本自由流动：允许资金自由进出本国市场。
- 固定汇率：保持本国货币与某一锚定货币（如美元）的汇率稳定。
- 独立的货币政策：中央银行能自主调节利率等工具来应对国内经济问题（如通胀或失业）。
三角关系：
- 选择资本自由流动 + 固定汇率：你必须放弃货币政策独立性。因为为了维持汇率稳定，当国际资本流入或流出时，你必须被动地调整货币供应量，使利率与国际市场趋同。（案例：香港联系汇率制）
- 选择固定汇率 + 独立的货币政策：你必须实行资本管制，限制资金自由流动。否则，国内外利差会导致套利资本剧烈冲击你的固定汇率。（案例：过去中国一定程度上的选择）
- 选择独立的货币政策 + 资本自由流动：你必须让汇率自由浮动，让汇率市场成为调节资本流动的缓冲器。（案例：美国、英国、日本）

结论：计算机如何"破解"不可能三角？

计算机系统并没有在物理上真正"破解"这个三角，而是用了一个巧妙的系统工程方法：分级存储体系。

这个方法的智慧在于：

承认矛盾：承认单一介质无法同时满足三者。
分层妥协：用不同特性的介质组成一个层次结构（金字塔）。
利用局部性原理：通过智能的数据调度（缓存、虚拟内存），让CPU在95%以上的时间都只与塔尖那容量极小但速度极快、成本极高的部分（寄存器、缓存）打交道。
实现宏观最优：从整个系统宏观视角看，它呈现给用户的体验是：

速度：接近最快的那一层（Cache）。
容量：接近最底层（硬盘/云存储）。
成本：接近一个由绝大部分廉价介质构成的系统的平均成本。

1.2. 您提到的两级存储体系（核心实践）

这恰恰是分级思想的具体体现，但目标略有不同：

A. Cache-主存层次

目的：解决CPU与主存之间的速度差距（Speed Gap）。
实现方式 ：由硬件自动管理，对程序员完全透明。
关键技术：缓存行、映射策略、替换算法（如LRU）。
效果：让CPU在绝大多数时间都能以接近Cache的速度访问到所需的数据，从而提升整体运算速度。

B. 主存-辅存层次（虚拟存储体系）

目的：解决主存容量不足的问题，为程序员提供一个比实际物理内存大得多的、统一的地址空间。
实现方式 ：由操作系统（硬件辅助） 管理，对应用程序透明。
关键技术：分页、分段、页面置换算法（如Clock算法）、缺页中断。
效果：程序可以像拥有超大内存一样编写和运行，无需担心物理内存的实际大小。将不常用的数据暂存到低速但大容量的辅存中。

1.3. 更宏观的分级视图

实际上，现代计算机的存储层次是一个更多级的金字塔结构，从上到下，速度递减、容量递增、成本递减：

复制代码

                     速度最快
                        ↑
    CPU寄存器    → 容量极小，成本极高
         ↓
    高速缓存（L1, L2, L3） → 您提到的 Cache-主存 级
         ↓
       主  存（DRAM）   → 核心工作区
         ↓
     固态硬盘（SSD）    → 现代辅存/外存
         ↓
  机械硬盘/网络存储/磁带 → 容量巨大，成本极低
                        ↓
                     速度最慢

1.4. 核心设计原理

整个分级体系高效运转依赖于两个关键的局部性原理：

时间局部性：某个数据被访问后，很可能在近期再次被访问。（例如：循环变量）
空间局部性：某个存储单元被访问后，其附近的存储单元也很可能在近期被访问。（例如：顺序执行的指令、数组遍历）

正是基于这些原理，系统才能大胆地将"近期可能用到的数据"从低速层级提前调入高速层级，使得CPU在绝大多数时间访问的数据都在高速存储中，从而在宏观上 实现了接近最快层级的速度、接近最大层级的容量、接近最底层级的平均成本这一近乎完美的目标。

总结来说，您的理解完全正确： 计算机通过Cache-主存解决速度矛盾 ，通过主存-辅存（虚拟内存）解决容量矛盾，二者结合巧妙地用合理的成本调和了速度与容量之间的根本冲突。这就是分级存储体系的精髓所在。

好的，详细解释局部性原理。这是计算机体系结构中最核心、最重要的原理之一，是整个分级存储体系（Cache、虚拟内存）乃至程序性能优化的理论基础。

局部性原理 指出：程序在执行时，对内存的访问并非完全随机的，而是倾向于成簇或可预测的。这种"非均匀"的访问模式，使得系统可以聪明地预测未来需要什么数据，并提前做好准备。

它主要分为两个方面：

1.4.1 时间局部性

定义：如果一个数据项（或内存位置）被访问，那么它在不久的将来很可能再次被访问。
通俗比喻：就像你最近几天正在读的一本书，你很可能会在明天继续读它，而不是去读一本十年前碰过的书。
程序中的典型体现 ：
1. 循环变量 ：for (int i=0; i<10000; i++) 中的 i 会被反复读写。
2. 函数调用：一个被频繁调用的函数，其指令代码会被反复执行。
3. 计数器、累加器：在统计或计算过程中反复使用的变量。
对硬件/系统的影响 ：正是基于时间局部性，Cache（缓存） 才会存在。当CPU从主存读取一个数据时，系统会把它保留在更快的Cache里，期待它很快被再次用到。如果预测正确，下次访问就直接从Cache命中，速度极快。

1.4.2 空间局部性

定义：如果一个数据项被访问，那么其地址附近的数据项（相邻或相近的内存位置）也很有可能在不久的将来被访问。
通俗比喻：就像你在查字典，当你找到单词"Apple"时，你很可能会顺便看看附近的"Application"或"Appliance"，而不是立刻跳到字典最后的"Zoo"。
程序中的典型体现 ：
1. 顺序执行：程序的指令在内存中通常是连续存放的。执行完一条指令，下一条指令的地址就是当前地址+1（或加一个固定长度）。
2. 数组遍历 ：访问数组 arr[0] 后，接下来很可能是 arr[1], arr[2]... 它们在内存中是连续存储的。
3. 结构体/对象访问：访问一个对象的某个字段后，很可能接着访问同一对象内的另一个字段，这些字段在内存中也是相邻的。
对硬件/系统的影响 ：基于空间局部性，系统在从低速存储读取数据时，不会只读请求的那个字节，而是会一次性读取一个连续的块（称为缓存行 或页面）。例如，CPU要读arr[0]时，Cache会一次性把包含arr[0]到arr[15]的整个缓存行（比如64字节）从主存加载进来。这样，当接下来访问arr[1]时，数据已经在Cache里了。

一个综合示例：遍历二维数组

这是理解两种局部性最经典的例子。假设有一个按行存储的数组 int a[100][100]。

写法A（行优先遍历）：

c 复制代码

for (i = 0; i < 100; i++) {
    for (j = 0; j < 100; j++) {
        sum += a[i][j]; // 先a[0][0], 然后a[0][1], a[0][2]...
    }
}

空间局部性极好 ：每次访问的元素在内存中都是连续的（a[i][j] 和 a[i][j+1] 地址相邻）。当a[i][j]被加载到Cache时，同一缓存行后续的多个元素也被加载，后续访问直接命中Cache。
时间局部性 ：循环变量 i, j, sum 被反复访问，也具备时间局部性。
性能：高。Cache利用率高，缺页中断少。

写法B（列优先遍历）：

c 复制代码

for (j = 0; j < 100; j++) {
    for (i = 0; i < 100; i++) {
        sum += a[i][j]; // 先a[0][0], 然后a[1][0], a[2][0]...
    }
}

空间局部性极差 ：相邻两次访问的元素在内存中相隔很远（a[i][j] 和 a[i+1][j] 相隔 100 * sizeof(int) 个字节）。每次访问几乎都不在同一缓存行，导致每次加载Cache只用了其中一个数据，Cache频繁失效，需要不断从主存读取新行。
性能：非常低。可能比写法A慢一个数量级以上。

这个例子生动地说明了，理解并利用局部性原理，是编写高性能程序的关键。

局部性原理在系统各级存储中的应用

CPU缓存（Cache）：
- 缓存行 （通常64字节）的设定，就是基于空间局部性。
- 缓存替换算法（如LRU）的有效性，依赖于时间局部性（最近用的，很可能再用）。
虚拟内存（主存-辅存）：
- 内存页 （通常4KB）的设定，是基于空间局部性（程序的一个代码段或数据段通常会集中在一段连续的地址空间）。
- 页面置换算法（如Clock）的有效性，依赖于时间局部性（最近活跃的页，很可能继续保持活跃）。
磁盘缓存/预读：
- 操作系统或磁盘控制器会预读文件连续的扇区到内存缓存，也是基于空间局部性（顺序读文件）。

局部性原理不是一个物理定律，而是一个被广泛观测到的、强有力的经验规律。

它是"预测"和"投机"的基础：让计算机系统能大胆地提前获取数据，用空间（额外的缓存）换时间。
它是分级存储体系成立的基石：如果没有局部性，Cache和虚拟内存的预取策略将完全失效，分级存储带来的性能提升会微乎其微。
它是程序员必须掌握的思想：从数据结构的布局（例如，使用数组 vs 链表），到算法的设计（例如，循环分块优化），再到系统架构，深刻理解局部性原理是进行高效优化的前提。

简而言之，局部性原理解释了为什么"缓存"这种技术是有效的，并指导着我们如何设计计算机的各个层次以及如何编写高效的代码。

1.4.3 系统是怎么实现局部性原理

系统是怎么知道哪些数据是最近访问，哪些数据是紧邻要访问的，然后将他们保留在更快的Cache，这正是计算机系统设计的精妙所在。系统本身并不能预知未来 ，它不知道你"将要"访问什么。但它基于局部性原理 和一套精巧的硬件机制，来预测并提前准备最可能被访问的数据。

这个过程主要由CPU内的内存管理单元和缓存控制器硬件 自动完成，对软件完全透明。其核心逻辑可以概括为：基于过去的访问模式，推断未来的访问需求。

下面我详细解释系统是如何做到这一点的：

核心机制：缓存行与地址映射

系统管理数据的基本单位不是单个字节，而是一个块，称为 "缓存行"（Cache Line，通常为64字节）。

当CPU需要读取某个地址的数据时，会发生以下步骤：

地址解析：CPU把目标内存地址发给缓存控制器。
检查缓存：控制器根据一套映射规则（直接映射、组相联、全相联），快速判断这个地址对应的数据块（缓存行）是否已经在Cache中。
命中或缺失 ：
- 缓存命中：数据已在Cache中，直接返回给CPU，极快完成。
- 缓存缺失：数据不在Cache中，触发"Cache Miss"。

最关键的第4步：处理缓存缺失

当发生缓存缺失时，系统不会只读取CPU请求的那个字（如4字节），而是会：

从更慢的主存中，一次性把包含目标地址的整个缓存行（64字节）全部加载到Cache中。
然后才将CPU需要的那部分数据返回。

为什么这么做？

这就是对空间局部性的笃定和利用。系统假设：既然你访问了地址A，那么你很可能马上会访问A+1, A+2...（比如遍历数组）。通过一次性加载一个块，如果预测正确，后续访问就直接命中Cache，收益巨大。即使预测错误，也只是多加载了一些无用数据，代价相对较小。

系统如何判断"哪些数据最近访问"并保留它们？

这依赖于缓存替换算法。当Cache已满，需要为新数据腾出空间时，必须决定"踢掉"哪一行旧数据。算法的目标就是踢掉"最不可能再用"的数据。常见的硬件实现算法有：

LRU（最近最少使用）：
- 原理：认为**最近被访问过的数据，短期内再次访问的可能性大**。因此优先淘汰最久没有被访问过(最少被使用的)的行。
- 硬件实现 ：为缓存中的每一行维护一个"年龄"计数器。每次某行被访问，其年龄置为最年轻（如0），其他行的年龄增加。需要淘汰时，选择年龄最大（计数器值最高）的那一行。由于精确LRU硬件开销大，实际中多用近似LRU（如分治策略）。
随机替换：
- 简单地随机选择一行进行淘汰。实现简单，硬件成本极低，在Cache很大时，性能有时意外地接近LRU。
FIFO（先进先出）：
- 像队列一样，淘汰最早进入Cache的行。它不考虑访问频率，不如LRU符合局部性原理。

现代CPU的Cache（尤其是LLC，末级缓存）通常使用高度优化的近似LRU或类LRU算法。 这些硬件电路持续、自动地跟踪每一行的访问历史，并做出替换决策。

更高级的预测：预取器

以上是"被动"响应CPU的请求。现代CPU还有更积极的"主动"预测部件------硬件预取器。

预取器像一个智能观察员，在后台分析CPU发出的内存访问流模式 。当它识别出某种规律时，会在CPU尚未发出请求前，就提前将数据从主存加载到Cache。

预取器识别的典型模式：

顺序流预取：发现CPU在连续访问地址A, A+64, A+128...（例如遍历数组）。预取器会预测接下来要访问A+192，并提前加载。
跨步流预取：发现CPU在以固定步长访问地址，如A, A+256, A+512...（例如访问结构体数组中的某个字段）。预取器会学习这个步长并提前获取后续数据。

预取器的关键特点：

纯粹基于硬件模式识别，软件无感知。
预测可能错误 。如果预取错误，只会造成一些不必要的内存带宽占用和可能的有用数据被换出，但不会导致程序出错，因为CPU只从正式请求的地址读取数据。预取数据只是"候选"。

软件可以施加的影响

虽然缓存管理是硬件自动的，但程序员可以通过优化数据结构和访问模式来大幅提高缓存的效率，这被称为 "缓存友好性编程"：

紧凑的数据结构：使用数组而非链表（更好的空间局部性）。
顺序访问：像之前例子提到的，按行遍历多维数组。
缓存分块：在处理极大数组时，将数据分成能装入L1/L2 Cache的小块进行处理，确保一块数据在被"踢出"前被反复用尽。
对齐：让数据结构的起始地址与缓存行对齐，避免一个数据结构横跨两行，造成两次读取。

总结

系统"知道"哪些数据重要，是通过一套硬件自动执行的、基于经验的、概率性的预测机制：

基础规则（强制性） ：任何被CPU访问的数据，其所在的整个缓存行都会被加载并保留在Cache中一段时间。
保留策略（基于历史） ：使用LRU等替换算法，倾向于保留最近被访问过的行。
主动预测（基于模式） ：硬件预取器分析访问模式，提前加载预测即将被访问的数据。

这一切的核心思想是：虽然无法确知未来，但"最近被访问的"和"地址相邻的"数据，在统计学上具有更高的再次访问概率。 计算机系统通过硬件固化的策略，赌这个概率事件经常发生。而事实证明，在结构良好的程序中，这个赌注的胜率非常高，从而使得分级存储体系取得了巨大的成功。

简而言之，Cache就像一个聪明的图书管理员：它不一定知道您明天具体要借哪本书，但它会把您今天借的书、以及书架上相邻的书放在最显眼、最容易拿到的地方，因为根据经验，这样做最能满足大多数读者的需求。

1.5 高速缓存Cache

高速缓存Cache用来存储当前最活跃的程序和数据，直接与CPU交互，位于CPU

和主存之间，容量小，速度为内存的5-10倍，由半导体材料构成。其内容是主存

内存的副本拷贝，对于程序员来说是透明的。

Cache由控制部分和存储器组成:

存储器存储数据
控制部分判断CPU要访问的数据是否在Cache中，在则命中，不在则依据一定的算法从主存中替换。
地址映射:在CPU工作时，送出的是主存单元的地址，而应从Cache存储器中读/写信息。这就需要将主存地址转换为Cache存储器地址，这种地址的转换称为地址映像，由硬件自动完成映射。

无论哪种映射方式，主存地址通常被划分为三部分（或两部分）：

映射方式	地址字段划分
直接映射	Tag（标记） + Index（行号/组号） + Offset（块内偏移）
组相联	Tag + Set Index（组号） + Offset
全相联	Tag + Offset（无Index字段）

1. 块内偏移Offset

含义：在块内查找数据的字节地址
公式：偏移位数 = log₂(块大小)
例如：块大小=32B → 偏移位=log₂32=5位，可寻址0~31字节

2. 标记位Tag

作用：与索引一起唯一标识一个主存块
组成：主存地址中除索引和偏移外的剩余高位部分
公式：
- 直接映射：标记位数 = 主存地址位数 - (索引位数 + 偏移位数)
- 全相联：标记位数 = 主存地址位数 - 偏移位数
- 组相联：标记位数 = 主存地址位数 - (组索引位数 + 偏移位数)

3. 索引位Index

作用：选择Cache中的块或组
公式：
- 直接映射：索引位数 = log₂(Cache总块数)
- 组相联：组索引位数 = log₂(组数)

设主存容量为1MB，Cache容量为16KB，块大小为32B，采用直接映射方式。

计算主存地址位数。

计算Cache总块数。

画出地址结构，标出标记、索引、偏移的位数。

解题步骤：

主存地址位数：
- 1MB = 2²⁰字节
- 地址位数 = log₂(1M) = 20位
Cache总块数：
- Cache容量16KB，块大小32B
- 块数 = 16KB / 32B = (16×1024) / 32 = 512块

地址结构：

偏移位：块大小32B → log₂32 = 5位
索引位：Cache有512块 → log₂512 = 9位
标记位：20 - 9 - 5 = 6位

地址结构图：

复制代码

┌──────────┬──────────┬───────┐
│  标记(6)  │ 索引(9)  │偏移(5)│
└──────────┴──────────┴───────┘

地址映射分为下列三种方法:

在讲解映射前，先明确 3 个关键地址结构（以 32 位主存地址为例，结构可拆分）：

Cache 中的一行，等同于主存中的一块。
主存中一块的大小有多大，Cache中的一行就有多大
主存地址：通常分为主存块标记 + 组号（或 Cache 块号） + 块内偏移
Cache 地址：通常分为 Cache 块号 + 块内偏移
块内偏移：主存块和 Cache 块的大小相同（如 64B），块内偏移用于定位块内具体字节，位数 = log⁡2(块大小)\log_2(\text{块大小})log2(块大小)。三种映射方式的块内偏移部分完全相同，差异集中在主存块到 Cache 块的映射规则。假设：主存块大小 = Cache 块大小 = 2b2^b2b B → 块内偏移占 bbb 位。
块的定义Cache 和主存会被划分成大小相等的固定区域，这个区域就叫块（比如 64B、128B 一块）。一个块包含多个字节（如 64B 块 = 64 个字节），这些字节在块内有连续的相对地址（0~63）块大小B=2bB = 2^bB=2b（字节）→ Offset = b 位
Cache总行数（Lines）：若Cache容量为 CCC 字节，块大小为 BBB 字节，则行数 =C/B= C / B=C/B。
主存组数：若Cache容量为 CCC 字节，块大小为 BBB 字节，则行数 =C/B= C / B=C/B。
Index位数 （直接/组相联）：
- 直接映射：Index位数 = log⁡2(Cache行数)\log_2(\text{Cache行数})log2(Cache行数)
- 组相联：若为 kkk 路组相联，则组数 = Cache行数 / k，Index位数 = log⁡2(组数)\log_2(\text{组数})log2(组数)
Tag位数 = 主存地址总位数 - Index位数 - Offset位数

块内寻址机制:

定位块内具体字节，是指在 Cache 和主存的块结构中，通过块内偏移地址找到该块里某一个具体字节数据的过程

复制代码

步骤1：整个地址分解
┌──────────────┬──────────────┬──────────────┐
│     标记      │     索引      │    块内偏移    │
└──────────────┴──────────────┴──────────────┘

步骤2：用"索引"找到Cache中的哪个块

步骤3：用"块内偏移"在块内定位具体字节
例如：偏移=5 → 取该块的第6个字节（从0开始）

主存地址为0x1234，Cache块大小32B，采用直接映射。

问：该地址在Cache块内的偏移量是多少？

计算：

块大小32B → 偏移位 = log₂32 = 5位
地址0x1234 = 二进制0001 0010 0011 0100
取最低5位：10100 = 十进制20

答案：该地址在块内的第20字节处（从0开始计数）。

某32位地址的计算机，Cache容量为64KB，块大小为16B，采用4路组相联 映射。

问：标记字段占多少位？

解题步骤：

已知条件：
- 主存地址位数 = 32位
- Cache容量 = 64KB
- 块大小 = 16B
- 路数 N = 4
计算：
- 偏移位 W = log₂16 = 4位
- Cache总块数 = 64KB / 16B = 4096块
- 组数 S = 总块数 / N = 4096 / 4 = 1024组
- 组索引位 = log₂1024 = 10位
- 标记位 = 32 - 10 - 4 = 18位

答案：标记字段占18位。

1.5.1 直接映射方式

主存的每个块只能映射到Cache中唯一固定的位置。

映射规则 ：Cache块号 = 主存块号 % Cache总块数
地址结构 ：标记位 | Cache索引 | 块内偏移
优点：硬件简单、查找速度快（只需比较一个标记）
缺点：冲突率高（容易反复替换）

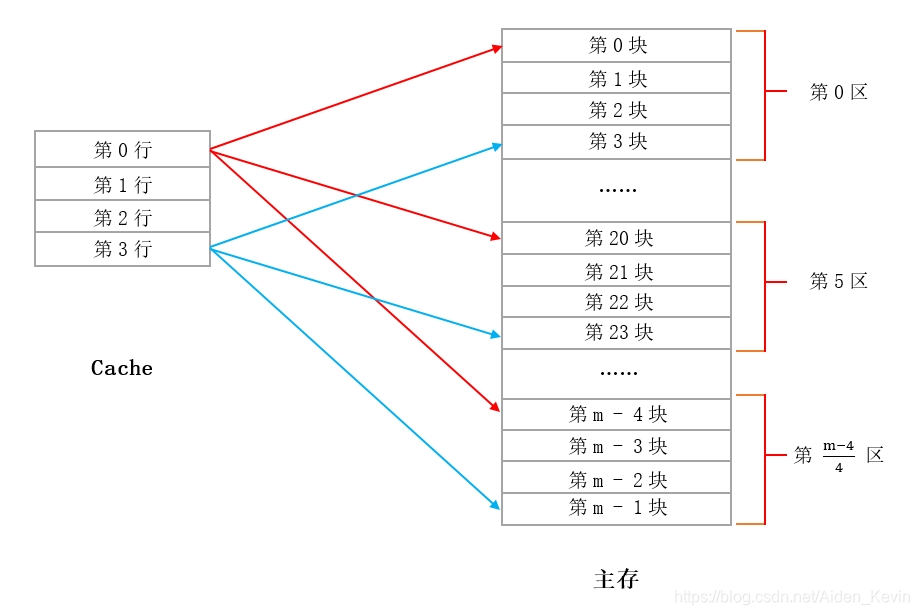
在直接映射中，我们将主存中分成了 m 块，每若干块组成了一个区（组），其中一个区中的块数取决于Cache中的行数。 Cache 中有多少行，我们的一个区就由多少块组成。（这里为了方便以 Cache 中只有 4 行举例，因为 Cache 只有 4 行，所以我们一个区也由 4 块组成 ) 如图所示，在直接映射中，每个区的第 0 块只能映射到Cache中的第 0 行，每个区的第 3 块只能映射到Cache中的第 3 行，也就是说主存中每个区的第 i 块会映射到Cache中的第 i 行，Cache 与主存之间是一对多的关系，这就是直接映射方式。

在 Cache 映射中：主存按块（Block）划分；Cache 按行（Line）划分（每行存一个主存块）；"组（Set）"这个概念主要用于组相联映射，直接映射中没有"主存分组"的说法。但在直接映射中，主存块号会通过取模运算映射到 Cache 的某一行。

在直接映射中，我们可以将主存的所有块按 Cache 行数进行"逻辑分区"（也叫"模类"或"同余类"），每个区内的所有主存块都映射到同一个 Cache 行。但这不是"主存物理分组"，而是根据映射规则自然形成的等价类

区数 = Cache 行数

📌 举个例子

主存块数 = 1000 块（编号 0 ~ 999）
Cache 行数 = 8 行

把主存块划分为 ( N ) 个逻辑区（或称"模类"）：

区 0：块号 0, N, 2N, 3N, ...
区 1：块号 1, N+1, 2N+1, 3N+1, ...
...
区 ( N-1 )：块号 ( N-1, 2N-1, 3N-1, \dots )

则主存可逻辑划分为 8 个区：

Cache 行	对应的主存块号（模 8 同余）
0	0, 8, 16, 24, ..., 992
1	1, 9, 17, 25, ..., 993
...	...
7	7, 15, 23, ..., 999

每个区大约有 ( 1000 / 8 = 125 ) 个块。

💡 类比理解

想象有 8 个邮箱（Cache 行），你要投递 1001 封信（主存块），规则是：

信编号 0 → 投 0 号邮箱
信编号 1 → 投 1 号邮箱
...
信编号 8 → 投 0 号邮箱（因为 8 mod 8 = 0）

问：有多少个邮箱被使用？

→ 答：8 个（即使只有 1 封信，也只用 1 个邮箱；但邮箱总数还是 8）

邮箱数量由系统决定（Cache 行数），不随信的数量改变！

Cache 行数（邮箱数）是固定的，但每个行可以被多个主存块"轮流使用"------它们不能同时存在，而是互相替换（冲突）。

所以：

1001 个主存块 ≠ 同时放进 Cache
Cache 只有 8 行 → 最多同时存 8 个块
其余 993 个块如果要进 Cache，必须替换掉已有的块

举例：

信 0 → 放格子 0
信 8 → 也要放格子 0 → 把信 0 踢出去，放信 8
信 16 → 还是格子 0 → 踢走信 8，放信 16
......

✅ 所以：虽然有 126 封信都想进格子 0，但同一时刻只有 1 封在里面！

信 0 → 放格子 0
信 8 → 也要放格子 0 → 把信 0 踢出去，放信 8
信 16 → 还是格子 0 → 踢走信 8，放信 16
......

✅ 所以：虽然有 126 封信都想进格子 0，但同一时刻只有 1 封在里面！

🔢 如果主存有：1001 块，Cache 8 行

主存块号：0 到 1000（共 1001 块）
Cache 行数：8（行 0 ~ 行 7）

每行"对应"的主存块数量（逻辑上）：

行 0：块 0, 8, 16, ..., 1000 → 共 126 块（因为 1000 ÷ 8 = 125 余 0，所以包含 0 和 1000）
行 1：块 1, 9, ..., 993 → 共 125 块
...
行 7：块 7, 15, ..., 999 → 共 125 块

✅ 所以：

"126" 是指有多少个主存块想映射到行 0
但 Cache 行 0 只能存其中一个（通常是最近访问的那个）
其他 125 个块如果要被访问，就必须把当前块替换出去

这就是 直接映射的冲突问题：多个主存块竞争同一个 Cache 行。

案例真题

主存容量为 4MB，块大小为 64B，Cache 采用直接映射，Cache 容量为 32KB。

问：主存共分为多少块？Cache 有多少行？主存块号 1000 映射到哪一行？

解：

主存块数 = ( \frac{4 \text{MB}}{64 \text{B}} = \frac{4 \times 2^{20}}{26} = 2^{22 - 6} = 2^{16} = 65536 ) 块
Cache 行数 = ( \frac{32 \text{KB}}{64 \text{B}} = \frac{2^{15}}{26} = 2^9 = 512 ) 行
主存块号 1000 → 映射到 Cache 行号 = ( 1000 \bmod 512 = 1000 - 512 \times 1 = 488 )

1.5.2 组相连映射方式

Cache分成若干组，每组有多个块（N路）。主存块映射到特定组 ，但可放在组内任意位置。

映射规则 ：组号 = 主存块号 % 组数
主存块号 ：主存地址/块大小
地址结构 ：标记位 | 组索引 | 块内偏移
优点：折中方案，最常用
N路组相联：每组有N块。组当N=1时退化为直接映射；当N=Cache总块数时退化为全相联。 "组（Set）"是 Cache 的结构，不是主存的！在组相联映射中，Cache 被划分为若干组（Set）；每组包含 N 行。组数=Cache总块数/N

假设有个主存块4GB,有 1600 多万个块，但它们都通过 mod 16 映射到这 16 个组中。

🧠 类比理解

想象：

你有一个书架（Cache），共 64 个格子；
你把书架分成 16 个大区（组），每个大区有 4 个小格子（4 路）；
全国图书馆有上亿本书（主存块）；
规定：每本书的编号 mod 16 决定它应该放在哪个大区；
但每个大区只能放 4 本书，满了就要替换。

→ 书架的"大区数"（16）是你自己设计的，和全国有多少本书无关！

✅ 正确公式总结

项目	公式	说明
Cache 组数	( \dfrac{\text{Cache 总块数}}{\text{路数 } N} )	✅ 仅由 Cache 决定
主存块数	( \dfrac{\text{主存容量}}{\text{块大小}} )	与组数无关
主存块映射到哪一组	( \text{主存块号} \bmod \text{Cache 组数} )	模的是 Cache 的组数

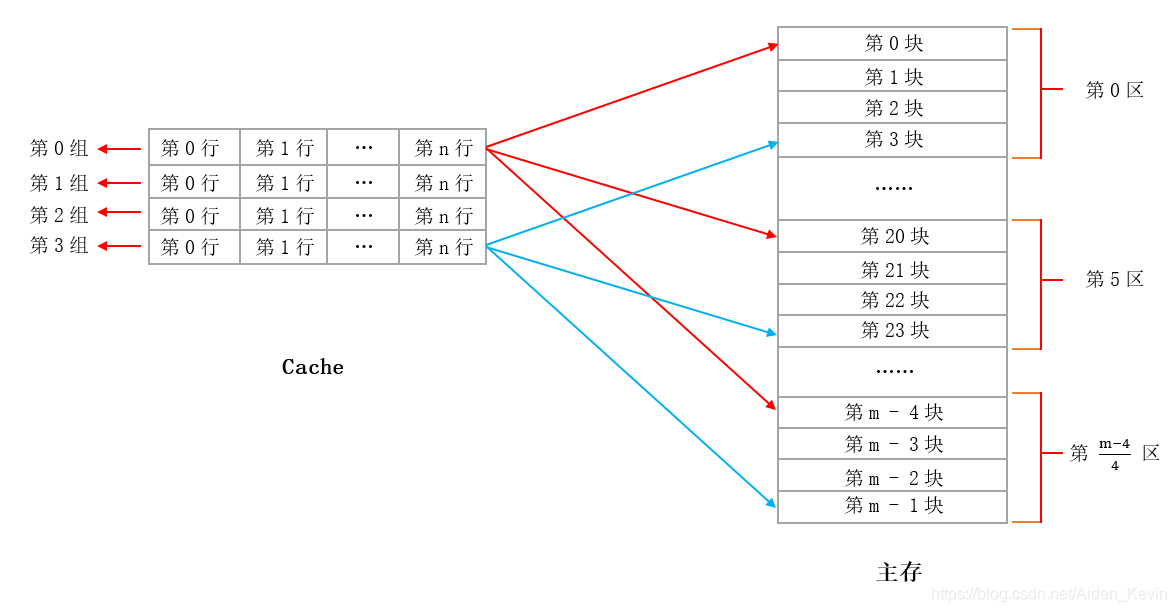
组相联映射基本和直接映射一样，也是将主存划分成了很多个区，唯一的不同就是 Cache 中若干个连续的行组成了一组，如上图所示。其中每个区中的第 i 块对应Cache中的第 i 组( 在直接映射中是每个区中的第 i 块对应Cache中的第 i 行，这点注意 )，在组相联映射中，我们可以将主存中每个区的一块随意存放在 Cache 中某一组的任意一行中。

某计算机的Cache共有16块，采用2路组相联映射方式，每个主存块大小为32字节，按字节编址。主存129号单元所在主存块应装入到Cache的哪一组？

解题：

分析参数：
- 总块数16，2路组相联 → 组数 = 16/2 = 8组
- 块大小32B → 偏移位5位
主存块号计算：
- 主存地址129
- 每块32字节 → 主存块号 = ⌊129/32⌋ = 4（第4块）
- 块内偏移 = 129 % 32 = 1
映射到Cache：
- 组号 = 主存块号 % 组数 = 4 % 8 = 4

答案：应装入Cache的第4组。

某32位地址的计算机，Cache容量为64KB，块大小为16B，采用4路组相联 映射。

问：标记字段占多少位？

解题步骤：

已知条件：
- 主存地址位数 = 32位
- Cache容量 = 64KB
- 块大小 = 16B
- 路数 N = 4
计算：
- 偏移位 W = log₂16 = 4位
- Cache总块数 = 64KB / 16B = 4096块
- 组数 S = 总块数 / N = 4096 / 4 = 1024组（N=4即每组有4块）
- 组索引位 = log₂1024 = 10位
- 标记位 = 32 - 10 - 4 = 18位

答案：标记字段占18位。

1.5.3 全相连映射方式

主存的每个块可以映射到Cache中任意位置。

地址结构 ：标记位 | 块内偏移（无索引字段）
优点：冲突率最低，空间利用率最高
缺点：查找速度慢（需比较所有标记），硬件成本高

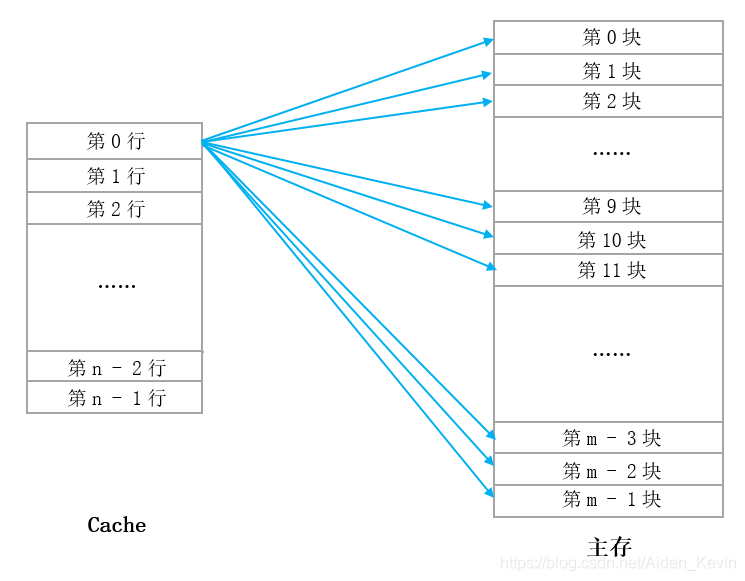
在全相联映射中，我们将主存分成了 m 块，将 Cache 分成了 n 行，Cache中的一行可以存放主存中的任意一块，如图 (1)。而反过来呢，主存中的一块可以存放在 Cache 中的任意一行，如图 (2) 。Cache 和主存之间是多对多的关系，也就是说 Cache 中的任意一行可以存放主存中的任意一块，这就是全相联映射方式。

假设：Cache 总块数 = 4，主存块号 = 5。

主存块 5 可映射到 Cache 块 0、1、2、3 中的任意一个；
若 Cache 块 1 空闲 → 放入 Cache 块 1；
若后续访问主存块 5 → 对比所有 Cache 块的标记，找到 Cache 块 1 匹配 → 命中。

某32位计算机，Cache容量为64KB，采用全相联映射，块大小为32B。

计算Cache总块数。

画出地址结构，标明各字段位数。

每个Cache行需要多少位存储标记？

解题步骤：

Cache总块数：
- Cache容量64KB = 65536字节
- 块大小32B
- 总块数 = 65536 / 32 = 2048块

地址结构：

32位地址
偏移位 = log₂32 = 5位
全相联没有索引字段
标记位 = 32 - 5 = 27位

地址结构图：

复制代码

┌──────────────────────────────┬───────┐
│          标记(27位)           │偏移(5)│
└──────────────────────────────┴───────┘

1.6 替换算法

替换算法的目标就是使Cache 获得尽可能高的命中率。常用算法有如下几种

(1)随机替换算法。就是用随机数发生器产生一个要替换的块号，将该块替换出去

(2)先进先出算法。就是将最先进入Cache 的信息块替换出去。

(3)近期最少使用算法。这种方法是将近期最少使用的Cache 中的信息块替换出去

(4)优化替换算法。这种方法必须先执行一次程序，统计Cache 的替换情况

有了这样的先验信息，在第二次执行该程序时便可以用最有效的方式来替换。

1.7 命中率及平均时间

Cache有一个命中率的概念，即当CPU所访问的数据在Cache中时，命中，直接从

Cache中读取数据，设读取一次Cache时间为1ns，若CPU访问的数据不在Cache中

则需要从内存中读取，设读取一次内存的时间为1000ns，若在CPU多次读取数据

过程中，有90%命中Cache，则CPU读取一次的平均时间为(90%*1 + 10%*1000)ns

1.8 存储系统中的单位

1B(字节)=8bit
KB = 1024B= xxx(B)/1024(2^10)=y(KB)
MB = 1024KB
G = 1024MB