文章目录
一、插入排序法简介
插入排序(Insertion Sort)是一种简单的排序算法,它通过将一个元素插入到已排序部分的合适位置来逐步完成排序。它的工作方式类似于整理扑克牌,当你拿到新的一张牌时,会将它插入到已经排序好的牌堆中。
插入排序的基本思想:
- 从第二个元素开始:假设第一个元素已经是一个已排序的子序列。
- 逐步插入每个新元素:从左到右遍历数组,取出当前元素,并将它与已排序部分的元素进行比较。
- 插入到正确位置:将当前元素插入到已排序部分合适的位置,保持已排序部分的顺序。
- 重复此过程,直到所有元素都排好顺序。
二、插入排序法演示排序过程
假设我们有一个数组 arr = [64, 25, 12, 22, 11],我们将通过几轮排序过程来展示插入排序的工作原理。
初始数组:
cpp
[64, 25, 12, 22, 11]第一次遍历:
选择第二个元素 25,与第一个元素 64 比较,发现 25 < 64,所以将 64 移动一位,25 插入到第一个位置:
cpp
[25, 64, 12, 22, 11]第二次遍历:
选择第三个元素 12,与已排序部分 [25, 64] 进行比较:
- 12 < 64,将 64 向右移。
- 12 < 25,将 25 向右移,12 插入到第一个位置
cpp
[12, 25, 64, 22, 11]第三次遍历:
选择第四个元素 22,与已排序部分 [12, 25, 64] 进行比较:
- 22 < 64,将 64 向右移。
- 22 < 25,将 25 向右移,22 插入到第二个位置
cpp
[12, 22, 25, 64, 11]第四次遍历:
选择最后一个元素 11,与已排序部分 [12, 22, 25, 64] 进行比较:
- 11 < 64,将 64 向右移。
- 11 < 25,将 25 向右移。
- 11 < 22,将 22 向右移。
- 11 < 12,将 12 向右移,11 插入到第一个位置
cpp
[11, 12, 22, 25, 64]最终排序结果:
cpp
[11, 12, 22, 25, 64]三、插入排序的时间复杂度分析
1.最坏情况时间复杂度:O(n²)
最坏情况发生在输入数组是逆序排列的情况下。每一轮都需要将当前元素与已排序部分的所有元素比较并移动,因此每次都需要做最多的 n-i 次比较和移动。所以总的比较次数为:
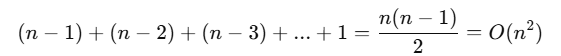
2.最好情况时间复杂度:O(n)
最好情况发生在输入数组已经是有序的情况下。此时每个元素都不需要移动,只需要进行一次比较。因此,最好情况的时间复杂度是 O(n)。
3.平均情况时间复杂度:O(n²)
平均情况下,插入排序的比较次数和交换次数都接近最坏情况,因此时间复杂度仍然是 O(n²)。
4.空间复杂度:O(1)
插入排序是原地排序算法,不需要额外的存储空间来存放临时数据,因此其空间复杂度为 O(1)。
插入排序特别适用于以下几种情况:
- 小规模数据集:当数据量较小时,插入排序因其简单和稳定性,往往能提供较好的性能。
- 部分有序数据:当数组已经有一定的顺序时,插入排序非常高效。例如,当数据已经部分排序,插入排序会非常迅速。
- 在线算法:插入排序是一个在线算法,可以逐步处理输入数据,不需要等待所有数据准备好。这在某些实时计算或逐步处理的应用中非常有用。
四、插入排序的代码实现
cpp
#include <iostream>
using namespace std;
void insertionSort(int arr[], int n) {
for (int i = 1; i < n; i++) {
int key = arr[i]; // 当前待插入的元素
int j = i - 1;
// 将大于 key 的元素移到右边
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
// 插入 key
arr[j + 1] = key;
}
}
int main() {
int arr[] = {64, 25, 12, 22, 11};
int n = sizeof(arr) / sizeof(arr[0]);
insertionSort(arr, n);
cout << "Sorted array: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}