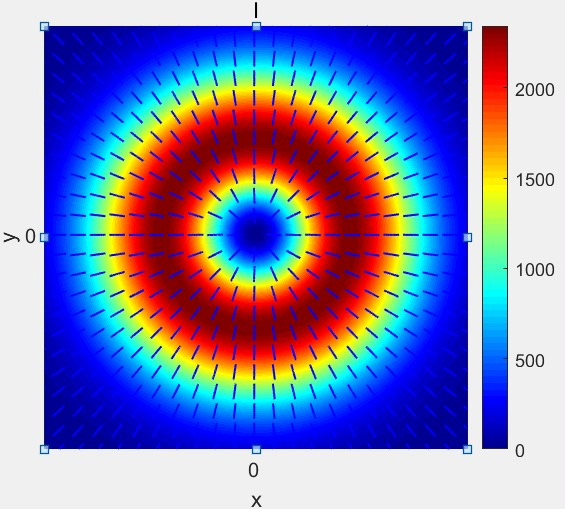
Matlab模拟矢量光束之径向偏振光束

打开Matlab准备画个径向偏振光束玩玩。这玩意儿的特点是电场矢量沿半径方向分布，就像无数箭头从圆心向外发射。先别急着敲代码，咱得把极坐标系转成直角坐标------Matlab画图还是直角坐标系顺手。

先整点基础参数：

matlab 复制代码

N = 512;   % 网格尺寸
lambda = 632e-9; % 波长
k = 2*pi/lambda;  % 波数
w0 = 1e-3; % 束腰半径
[x,y] = meshgrid(linspace(-2e-3,2e-3,N)); % 生成2mm见方的网格

这里故意把坐标范围设成±2mm是为了防止边缘截断，后面算相位分布时才不会出幺蛾子。接着把直角坐标转极坐标：

matlab 复制代码

[theta, rho] = cart2pol(x,y); % 关键转换函数

重点来了！径向偏振的横向电场分量得这么算：

matlab 复制代码

Ex = rho.*cos(theta).*exp(-(rho.^2)/(w0^2));
Ey = rho.*sin(theta).*exp(-(rho.^2)/(w0^2));

注意看cos(theta)和sin(theta)这对组合，这就是把径向矢量分解成x、y分量的精髓。exp项是高斯包络，rho乘在前面让中心场强归零------典型的径向偏振特征。

想看效果？用quiver画矢量图：

matlab 复制代码

sample_step = 20; % 抽样步长避免箭头太密
quiver(x(1:sample_step:end,1:sample_step:end),...
       y(1:sample_step:end,1:sample_step:end),...
       Ex(1:sample_step:end,1:sample_step:end),...
       Ey(1:sample_step:end,1:sample_step:end));
axis square; colormap jet;

但这么直接画可能发现箭头大小不一致，得做个归一化处理：

matlab 复制代码

E_norm = sqrt(Ex.^2 + Ey.^2);
Ex_norm = Ex./E_norm;
Ey_norm = Ey./E_norm;

替换掉原来的Ex/Ey再画矢量图，这下箭头长度就统一了，方向分布更清晰。

进阶玩法可以加相位涡旋：

matlab 复制代码

l = 1; % 拓扑荷数
phase = exp(1i*l*theta);
Ex = Ex .* phase;
Ey = Ey .* phase;

这样处理后的光束携带轨道角动量，用imagesc(angle(Ex))能看到漂亮的螺旋相位分布。不过要注意实部虚部得分开处理，做传播仿真时得用复数场。

最后提醒下，内存不够的把N调小点，512*512的矩阵在低配电脑上可能会卡。遇到箭头方向混乱的，检查下theta的计算是否正确------有时候cart2pol返回的角度范围在(-π, π]，而用atan2可能会更直观些。