使用AI辅助开发SDR-多相滤波DDC/DUC工具核心原理详解

在软件无线电(SDR)开发中，数字下变频(DDC)和数字上变频(DUC)是两个核心功能模块。它们负责在不同采样率的信号之间进行转换，同时完成频率搬移。本文将从工程实现角度，详解多相滤波技术在DDC/DUC中的应用，以及为什么它比传统方法更高效。该工具的创作过程是和AI共同完成的，核心的滤波器索引部分进行了关键的人为修整。

下图是使用本文介绍的算法，实现3个不同速率的波形调整到1个大采样率下并合路输出的仿真例子。其代码参考 taskBus 里 modules/transforms/reampler_ddcduc。

其发行版可以在这里找到： https://gitcode.com/colorEagleStdio/taskbus/releases

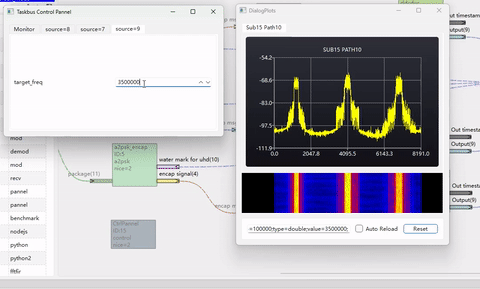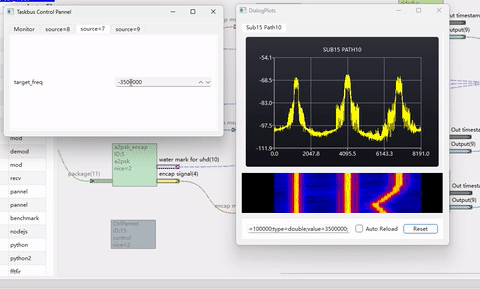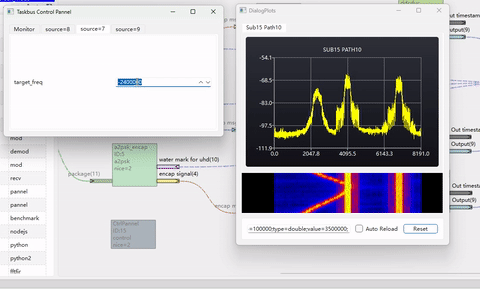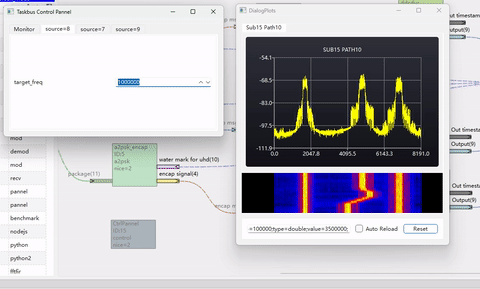
由于AI问答思考过程非常冗长，这里从略。此外，驱动AI进行编程，产生多项滤波器需要具备比较强的通信理论知识，并对其设计思路进行控制，否则容易原地打转，甚至聋子治哑越治越哑！

注意：3路duc超过了4核心CPU的处理能力，只能用小速率进行测试。真的要驱动B210在5MHz甚至10MHz下发射，还需要多核心服务器/工作站的支持，如配备AMD Ryzen 9 9950X的DDR5 Linux 6.12 RT内核旗舰工作站。

1 从传统滤波到多相滤波：为什么需要改进？

假设我们有一个采样率为1MHz的信号，想要将其转换为250kHz，这需要进行4倍抽取(即每4个点保留1个)。传统做法是：

1. 先对信号进行低通滤波，防止抽取时产生混叠
2. 然后每隔3个点取1个点

看起来很简单，但实际操作中会有大量冗余计算。例如，假设滤波器长度为16，每个输入点都需要与16个系数相乘再相加，但最终我们只保留1/4的结果。这意味着有3/4的计算是白费的！

多相滤波技术正是为了解决这个问题而诞生的，它能巧妙地避开这些无用计算，大幅提高效率。

2. 多相滤波的本质：数学原理通俗解释

多相滤波的核心思想可以用一句话概括：将滤波器拆解后与抽取/插值操作交换顺序，减少冗余计算。

让我们用一个简单例子说明。假设我们要实现3倍插值后再2倍抽取(总体是3/2倍的采样率转换)：

传统方法流程：输入 → 插值(补零) → 低通滤波 → 抽取 → 输出

多相滤波则是：输入 → 计算周期 → 周期内各个样点分别处理 → 输出

2.1 滤波器"分身术"的本质

书上说，"多相滤波会将一个完整的FIR滤波器拆分成多个"子滤波器"(称为相)。如果我们的插值因子是L，抽取因子是M，就会得到L个并行的子滤波器。"

但是，我不喜欢这个说法。太数学了，容易误导人硬是往sin cos的"相位"的"相"上去想。实际上，完全可以更符合程序猿的思维：

假设滤波器的长度是N，对原始信号的每个样点之间，插入L-1个零，得到周期为L的上插序列S。而后，以周期M进行抽取，产生结果序列。在对S以周期M进行抽取时，卷积计算窗口覆盖范围内的非零的元素的位置搭配是有限的、可提前计算的。举例：

以L=2, M=3为例，序列 ABCDEFGHI首先变成:

A 0 B 0 C 0 D 0 E 0 F 0 G 0 H 0 I 0 J 0.

而后，以M=3为周期抽取，位置如下：

A 0 B 0 C 0 D 0 E 0 F 0 G 0 H 0 I 0 J 0.

1     1     1     1     1     1     1

假设滤波器的长度为5，则每次计算时，参与计算的非0元素：

Z 0 A 0 B 0 C 0 D 0 E 0 F 0 G 0 H 0 I 0 J 0.
    |
a b c b a = aZ + cA + aB
    
    A 0 B 0 C 0 D 0 E 0 F 0 G 0 H 0 I 0 J 0.
          |
      a b c b a = bB + bC

    A 0 B 0 C 0 D 0 E 0 F 0 G 0 H 0 I 0 J 0.
                |
            a b c b a = aC + cD + aE

    A 0 B 0 C 0 D 0 E 0 F 0 G 0 H 0 I 0 J 0.
                      |
                  a b c b a = bE + BF
     ......  

可以看到，参与计算的滤波器元素、原始序列的搭配图案周期重复出现，每次有最多 M=3 个非零计算，全部的情况以M * L = 6 反复出现。因此，我们只要记住L种不同的组合方式要取的非0滤波器系数、参与计算的原始数据相对窗口的位置，就能直接进行查表计算。在代码中，这体现在GeneralPolyphaseFIR类的实现中：

// 拆分多相系数：将完整FIR系数分配到L*M为周期的时钟里
std::vector<std::vector<int>> m_mul_clks;    // 存储每个相的时钟索引
std::vector<std::vector<double>> m_mul_flts; // 存储每个相的滤波器系数

这些子滤波器就像滤波器的"分身"，各自处理一部分计算，最后再将结果组合起来。而这些非0位置的确定，是通过仿真直接暴力确定的，比自己推规律靠谱、直接：

	   std::map<int,int> simu_clks;
		const int filter_len = fir_coeffs.size();
		//产生插0后的序列时钟索引。这个时钟clk是L倍插0后的时钟
		for (int clk = -filter_len - M - L; clk <= M * L + filter_len;++clk )
		{
			if (clk % L ==0)
    			//记录的非0时钟是原始数据的时钟（插0前）
				simu_clks[clk] = clk / L;
			else
			   //0位置用max int表示，不和可能为0、正数（滤波器右侧）、负数（滤波器左侧）的 clk/L冲突
				simu_clks[clk] = 0x7fffffff;
		}
		int half_fir = fir_coeffs.size()/2;
		int sz_fir = fir_coeffs.size();
		
		//计算 clk位于 0-M*L内，哪些元素参与运算
		int need_max = 0;
		for (int clk = -filter_len - M - L; clk <= M * L + filter_len;++clk )
		{
			if (clk<0) continue;
			if (clk>=M*L)	break;
			if (clk % M)		continue;
			const int produce = clk / M;
			std::vector<int> v_clks;
			std::vector<double> v_flts;
			for (int psclk = -half_fir;psclk <= half_fir; ++psclk)
			{
				int cal_clk = clk + psclk;
				int fir_pos = psclk + half_fir;
				if (simu_clks[cal_clk]==0x7fffffff || fir_pos >=sz_fir)
					continue;
				v_clks.push_back(simu_clks[cal_clk]);
				v_flts.push_back(fir_coeffs[fir_pos]);
			}
			m_mul_clks.push_back(v_clks);
			m_mul_flts.push_back(v_flts);
			if (need_max < v_clks.size())
				need_max = v_clks.size();
		}
		m_need_max = need_max / 2 + 2;
		m_ringBuf.resize(next_power_of_two( m_need_max + M * L));
		ringBufSz = m_ringBuf.size();
		mask = ringBufSz - 1;
		m_bufptr = m_ringBuf.data();

2.2 多相滤波为什么更快？关键在"0元素排除"

从上文看到，多相滤波比传统卷积快的核心原因是它能预先知道哪些计算是无效的(乘以0)，从而彻底跳过这些计算。

当我们进行L倍插值时，实际上是在每两个原始样本之间插入L-1个0。传统卷积会认真地将滤波器系数与这些0相乘，这完全是浪费时间。

多相滤波通过数学变换，将滤波器拆解后，这些0元素会被自动排除在计算之外。上面这段代码的作用是：

1. 遍历所有可能的时钟位置
2. 只保留那些最终会产生输出的时刻
3. 对每个有效时刻，只记录需要参与计算的输入位置和对应系数

通过这种预计算，在实际处理时，我们只需要进行必要的乘法运算，完全跳过了与0相乘的步骤。这就是多相滤波效率高的根本原因！

3. 工程实现的关键技术

3.1 环形缓存：高效的数据存取方式

在信号处理中，我们需要经常访问历史数据(因为滤波器计算需要多个输入样本)。如果每次都重新分配内存或移动数据，效率会很低。环形缓存(也叫循环缓冲区)就是解决这个问题的最佳方案。

std::vector<T> m_ringBuf;  // 环形缓存
size_t ringBufSz = 0;
size_t mask = 0;
T* m_bufptr = 0;

// 初始化环形缓存
m_ringBuf.resize(next_power_of_two(m_need_max + M * L));
ringBufSz = m_ringBuf.size();
mask = ringBufSz - 1;  // 用于快速取模运算
m_bufptr = m_ringBuf.data();

环形缓存的精妙之处在于：

• 使用2的幂作为大小，通过& mask操作实现快速取模
• 不需要移动数据，只需更新读写指针
• 自动覆盖过期数据，无需手动管理内存

当需要访问位置pos的数据时，只需计算pos & mask，就能得到在环形缓存中的实际索引，既快速又方便。

3.2 提前准备索引：避免实时计算开销

多相滤波的另一个效率提升点是提前计算好所有需要访问的索引，而不是在实时处理时临时计算。

在GeneralPolyphaseFIR类中，m_mul_clks存储了每个相位计算时需要访问的历史数据索引：

/**
		 * 核心处理函数：输入样本，输出若干个重采样后的样本
		 * @param in 输入样本（输入采样率）
		 * @param out 输出样本列表（输出采样率）
		 * @return 输出样本个数
		 */
	inline size_t resample(const T& in, std::vector<T>& out) {

		m_bufptr[m_clk_push & mask /*% ringBufSz*/] = in;
		++m_clk_push;

		const size_t sz_out = out.size();
		size_t produced = 0;

		while (m_clk_pop + M + m_need_max < m_clk_push )
		{
			for (int i=0;i<L;++i)
			{
				int * mul_clks = m_mul_clks[i].data();
				double * mul_flts = m_mul_flts[i].data();
				int pts =  m_mul_clks[i].size();
				T sum {0,0};
				for (int j=0;j<pts;++j)
				{
					size_t pos = size_t(m_clk_pop + mul_clks[j]) & mask;//% ringBufSz;
					sum.I += m_bufptr[pos].I * mul_flts[j];
					sum.Q += m_bufptr[pos].Q * mul_flts[j];
				}
				if (produced < sz_out)
					out[produced] = sum;
				else
					out.push_back(sum);
				++produced;
			}
			m_clk_pop += M;
		}
		return produced;
	}

这种预计算策略有两个好处：

1. 避免了实时处理时的复杂计算，降低了CPU负担
2. 可以在初始化时验证索引的有效性，提高了代码的健壮性

3.3 维护无限长的时钟节拍

在信号处理中，我们需要处理连续不断的数据流，就像有一个永远不会停止的时钟在计数。代码中使用了两个64位无符号整数来模拟这个无限时钟：

size_t m_clk_push {0};  // 记录输入数据的时钟
size_t m_clk_pop {0};   // 记录输出数据的时钟

• m_clk_push：每输入一个样本，就加1
• m_clk_pop：每输出一组样本，就增加M(抽取因子)

这种设计的巧妙之处在于：

1. 使用无符号整数的自然溢出特性模拟无限计数
2. 不需要处理复杂的_wrap逻辑，简化了代码
3. 通过比较两个时钟的差值，判断是否有足够的数据可以处理

// 检查是否有足够的数据可以处理
while (m_clk_pop + M + m_need_max < m_clk_push) {
    // 处理并生成输出数据
    // ...
    m_clk_pop += M;  // 移动输出时钟
}

3.4 AI设计适合极端高采样率的窄低通

对于L,M互质、L很大的情况，滤波器的阶数会很高，且需要采用凯泽窗，贝塞尔插值。

该滤波器由AI实现，几乎没有修改。唯一的修改是提高了奈奎斯特带宽为IQ路的1倍，而非2倍。

// FIR低通滤波器系数生成函数（优化版：适配L>60，凯泽窗+动态过渡带宽）
inline std::vector<double> generate_fir_lp_coeffs(
	double Fs_in,        // 输入采样率（Hz）
	size_t L,            // 插值因子（FIR工作采样率 = Fs_in * L）
	double Fc,           // 通带截止频率（Hz）
	double Rp = 0.1,     // 通带波纹（dB）
	double Rs = 80.0,    // 阻带衰减（dB）
	size_t MAX_FIR_ORDER = 8192  // FIR最大阶数（可调整）
	) {
	// 1. 核心参数计算
	const double Fs_fir = Fs_in * L;
	const double Fnyquist = Fs_fir /*/ 2.0*/;
	double Fc_norm = Fc / Fnyquist;
	// 限制归一化截止频率≤0.45（避免靠近Nyquist频率，减少混叠）
	Fc_norm = std::min(Fc_norm, 0.45);

	// 2. 动态过渡带宽（避免L>60时阶数爆炸）
	const double min_transition_band = Fs_in * 0.002;  // 最小过渡带宽（输入采样率的0.2%）
	const double transition_band = std::max(Fc * 0.05, min_transition_band);
	const double BW_norm = transition_band / Fnyquist;

	// 3. 阶数估算（凯泽窗公式，比布莱克曼窗更精准）
	size_t N = 0;
	if (Rs >= 21.0) {
		// 凯泽窗阶数公式：N ≈ (Rs - 8.7) / (2.285 * π * BW_norm)
		N = static_cast<size_t>(std::round((Rs - 8.7) / (2.285 * M_PI * BW_norm)));
	} else {
		N = static_cast<size_t>(std::round(1.3 / BW_norm));  // 低衰减时退化为汉宁窗公式
	}

	// 阶数优化：对齐L的整数倍+保证奇数+不超过上限
	N = std::min(N, MAX_FIR_ORDER);
	// 对齐L的整数倍（避免多相拆分补零）
	if (N % L != 0) {
		N = ((N / L) + 1) * L;
	}
	// 保证奇数（线性相位）
	if (N % 2 == 0) {
		N += 1;
		if (N > MAX_FIR_ORDER) {
			N = ((MAX_FIR_ORDER - 1) / L) * L + 1;
		}
	}
	const size_t half_N = N / 2;

	// 4. 生成理想低通系数（sinc函数，优化数值精度）
	std::vector<double> coeffs(N, 0.0);
	for (size_t n = 0; n < N; ++n) {
		const int32_t k = static_cast<int32_t>(n) - static_cast<int32_t>(half_N);
		if (k == 0) {
			coeffs[n] = 2.0 * Fc_norm;  // 简化：sinc(0)=1，h(0)=2Fc_norm
		} else {
			const double arg = 2.0 * M_PI * Fc_norm * k;
			// 优化sinc计算：避免k过大时的数值振荡（用std::sin的高精度实现）
			coeffs[n] = (2.0 * Fc_norm) * (std::sin(arg) / arg);
		}
	}

	// 5. 应用凯泽窗（适配窄过渡带宽+高衰减）
	double beta = 0.0;
	if (Rs >= 50.0) {
		beta = 0.1102 * (Rs - 8.7);
	} else if (Rs >= 21.0) {
		beta = 0.5842 * std::pow(Rs - 21.0, 0.4) + 0.07886 * (Rs - 21.0);
	}
	const double bessel_0 = std::cyl_bessel_i(0, beta);  // 预计算贝塞尔函数值，避免重复计算
	for (size_t n = 0; n < N; ++n) {
		const int32_t k = static_cast<int32_t>(n) - static_cast<int32_t>(half_N);
		const double x = static_cast<double>(k) / half_N;
		const double window = std::cyl_bessel_i(0, beta * std::sqrt(1.0 - x * x)) / bessel_0;
		coeffs[n] *= window;
	}

	// 6. 归一化（优化数值稳定性：用Kahan求和法减少累积误差）
	double sum_coeff = 0.0;
	double correction = 0.0;  // Kahan求和：补偿浮点数加法误差
	for (double c : coeffs) {
		const double y = c - correction;
		const double t = sum_coeff + y;
		correction = (t - sum_coeff) - y;
		sum_coeff = t;
	}
	if (std::abs(sum_coeff) > 1e-12) {  // 避免除以极小值（数值稳定性）
		for (double& c : coeffs) {
			c *= L;
			c /= sum_coeff;
		}
	}

	return coeffs;
}

4. 完整工作流程：从参数到输出

让我们把这些技术点串联起来，看看一个完整的重采样过程是如何工作的：

1. 初始化阶段：

   • 根据输入输出采样率计算L(插值因子)和M(抽取因子)
   • 生成低通滤波器系数
   • 将滤波器拆分为L个相，预计算每个相的索引和系数
   • 初始化环形缓存

2. 处理阶段：

   • 接收输入样本，存入环形缓存，更新m_clk_push
   • 检查是否有足够的数据可以处理
   • 对每个需要输出的时刻，使用对应相的预计算索引和系数进行计算
   • 输出结果，更新m_clk_pop

3. 频率转换：

   • 使用NCO(数控振荡器)生成需要的载波
   • 与重采样后的信号进行混频，实现频率搬移

5. 实际应用：命令行参数与运行

在实际使用这个工具时，我们可以通过命令行参数来配置各种参数：

resample_ddcduc --function=resample_ddcduc --old_spr=2000000 --new_spr=192000 --target_freq=0 --band_width=192000 --type=1 --sptype=0

其中：

• --old_spr：输入信号采样率
• --new_spr：输出信号采样率
• --target_freq：目标频率
• --band_width：信号带宽
• --type：信号类型(实信号/复信号)
• --sptype：采样点格式

程序会根据这些参数自动计算L和M，生成合适的滤波器，并完成重采样和频率转换工作。

5.1 应用效果

多相滤波技术通过巧妙的数学变换，将传统滤波中大量冗余的计算剔除，显著提高了SDR中DDC/DUC的处理效率。其核心思想包括：

1. 将滤波器拆解为多个子滤波器，并行处理
2. 预计算有效索引，彻底排除与0相乘的无效操作
3. 使用环形缓存高效管理历史数据
4. 用两个时钟计数器跟踪输入输出进度，模拟无限长数据流

这些技术不仅让信号处理更高效，也展示了如何将数学理论转化为实际的工程实现。对于初学者来说，理解这些原理不仅能帮助使用现有的工具，更能为今后设计更复杂的信号处理系统打下基础。

通过AI辅助开发，我们可以更快速地实现这些复杂算法，并通过自动生成的代码框架，专注于核心逻辑的优化和验证，大大提高了开发效率。

5.2 在 taskBus SDR中应用

在 taskBus里，可以进行仿真，查看duc/ddc的效果。

下面这个例子里，产生了3路不同速率的调相波形，并上采样到同一个采样率下，进行合路。通过调整移频因子，可以实时改变某个载波的位置。

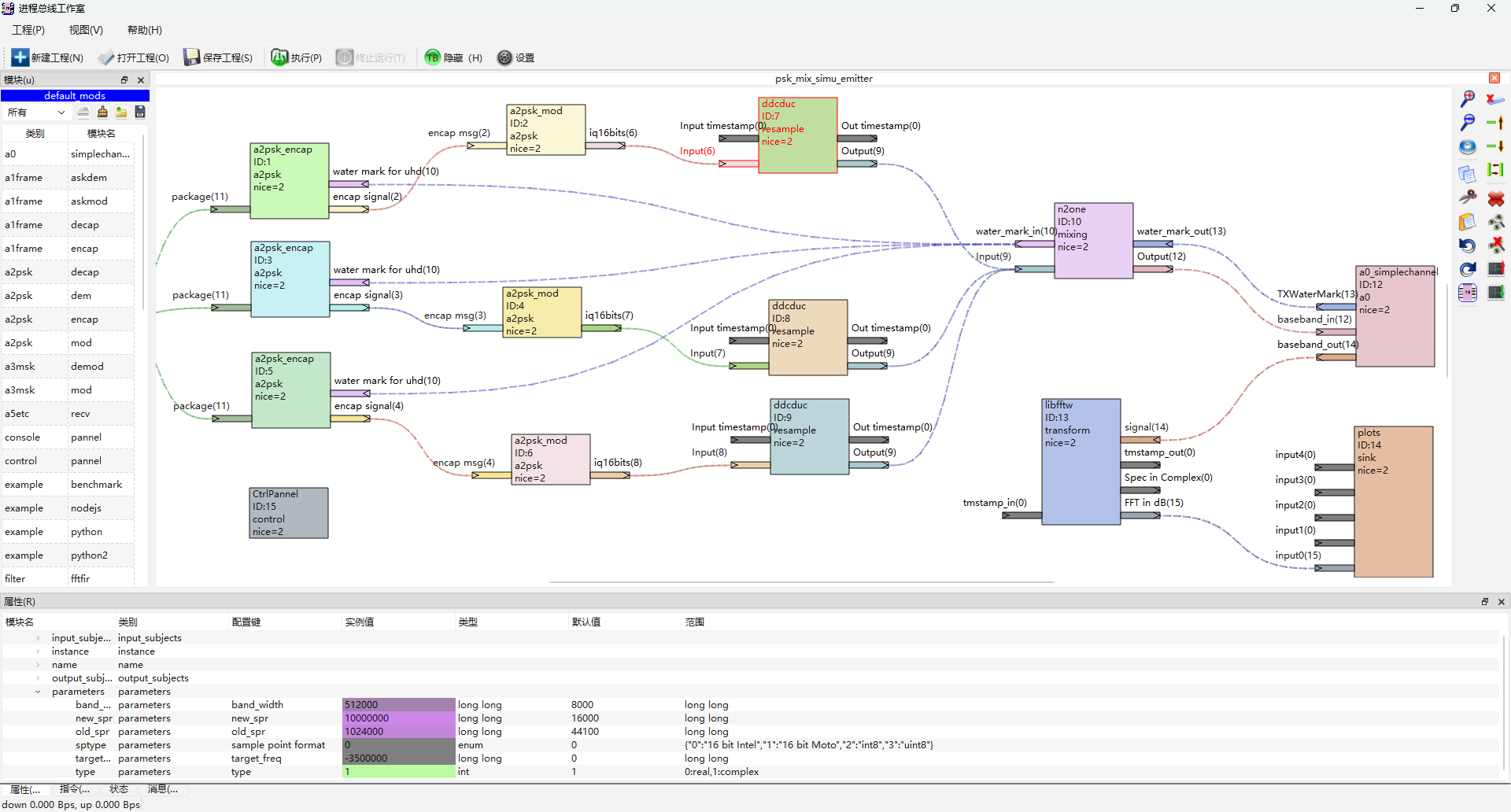
6. 水位控制-工程实现额外的复杂性

6.1 n2one合路模块的双向水位控制原理

（1）水位控制的核心作用

在n2one多路信号合路过程中，双向水位控制是保障数据处理流畅性、避免缓冲区溢出或数据饥饿的关键机制。其核心目标是通过动态监测和调节数据输入输出节奏，实现多路信号的高效融合，同时确保上下游模块间的数据流转平衡。

(2) 双向水位控制的构成

n2one模块的双向水位控制包含两个关键方向：

1. 输入水位控制（water_mark_in）：模块向源头反馈自身处理能力，避免上游数据输入过快导致缓冲区溢出
2. 输出水位控制（water_mark_out）：接收下游模块的水位反馈，调节自身输出节奏，避免下游处理不及

6.2、输入水位控制机制

1. 数据监测：

   • 模块实时跟踪各输入通道（path_id）的数据位置（path_pos）
   • 计算每个通道当前数据量与输出位置的差值（w = p->second - out_clk）

2. 反馈机制：

   • 通过water_mark_in主题周期性向上游推送各通道的水位信息
   • 推送频率为每10000次循环一次，数据格式为64位无符号整数
   • 上游模块根据反馈的水位值调节数据发送速率

3. 实现代码片段：

if (iwater_mark_in) {
    static long long clkkk = 0;
    ++clkkk;
    for(auto p = path_pos.begin();p!=path_pos.end();++p) {
        unsigned long long w = p->second - out_clk ;
        TASKBUS::push_subject(
            iwater_mark_in,
            (unsigned int)p->first,
            sizeof(qint64),
            (unsigned char*)&w
        );
    }
}

6.3 输出水位控制机制

1. 数据接收：

   • 通过water_mark_out主题接收下游模块的水位信息
   • 仅处理属于当前实例（header.path_id == instance）的水位数据

2. 调节逻辑：

   • 当设置了最小水位阈值（minmark > 0）时，若下游水位（g_watermark）超过阈值，则暂停输出
   • 直到下游水位低于阈值时，才继续处理和输出数据

3. 实现代码片段：

// 水位控制
if (minmark > 0 && iwater_mark_out > 0) {
    if (g_watermark > minmark)
        continue;
}

6.4 双向协同工作流程

1. 模块初始化时，通过命令行参数获取water_mark_in和water_mark_out的主题ID

2. 运行过程中：

   • 持续接收多路输入数据并存储到环形缓冲区
   • 定期向上游反馈各通道的输入水位
   • 接收下游的输出水位反馈并据此调节输出节奏
   • 当所有输入通道都有足够数据时，计算混合结果并输出

3. 关键平衡点：

   • 输入水位反馈防止上游数据积压
   • 输出水位控制防止下游处理过载
   • 环形缓冲区作为中间缓冲，缓解上下游速度差异

这种双向水位控制机制使n2one模块能够自适应上下游的数据处理能力，在多路信号合路场景中实现高效、稳定的数据流转。