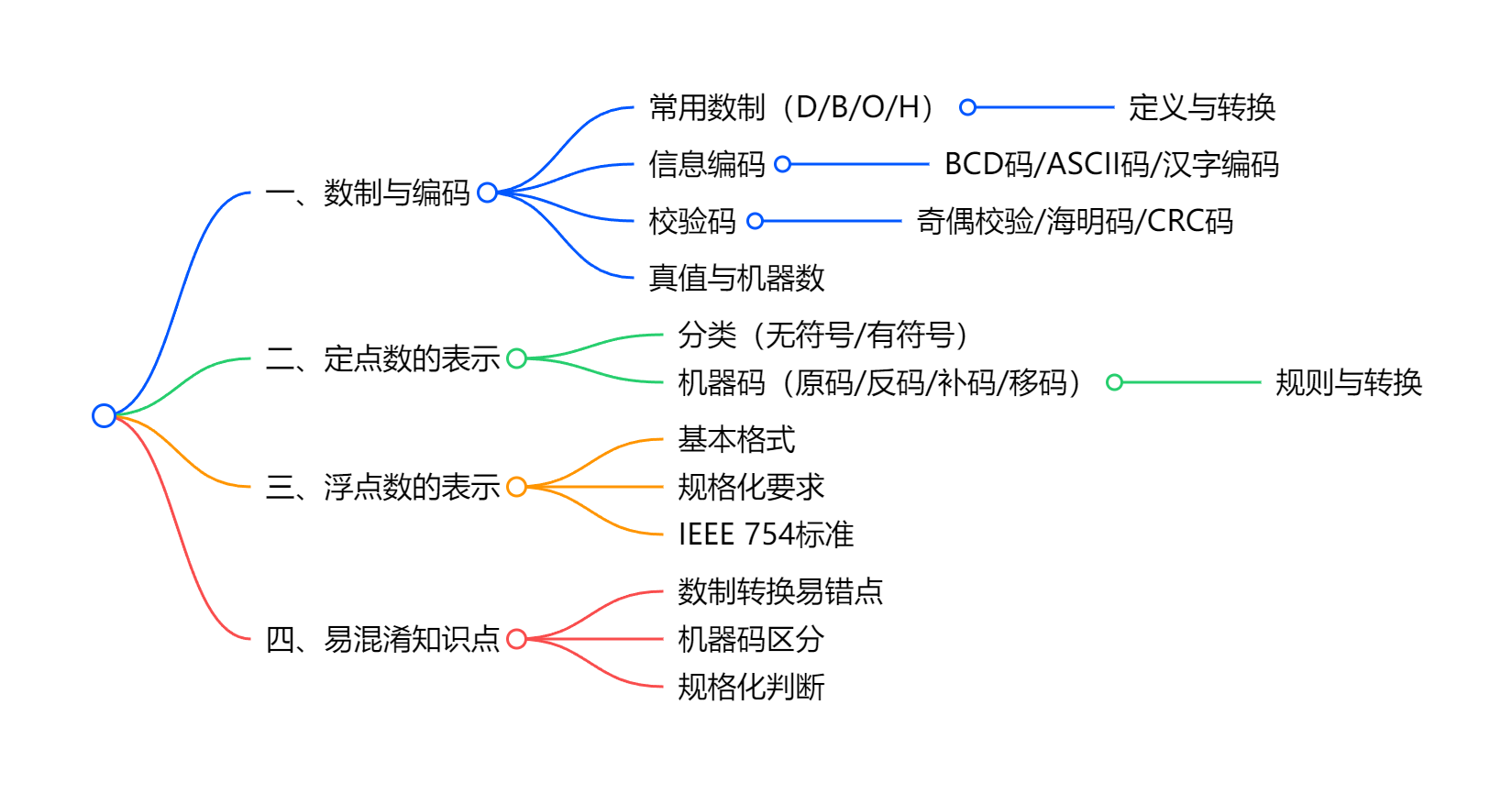
本章核心围绕计算机中数据的编码规则与表示方法展开,重点掌握数制转换、机器码表示、定点 / 浮点数格式及校验码应用,以下是结构化重点提炼及思维导图框架:
一、数制与编码(核心应用层)
1. 常用进位计数制
- 四大数制:十进制(D)、二进制(B)、八进制(O)、十六进制(H)
- 核心概念:基数(符号个数)、权(位值系数)
- 转换规则:
- 非十进制→十进制:按权展开求和
- 十进制→二进制:整数 "除 2 取余",小数 "乘 2 取整"
- 二 / 八 / 十六进制互转:3 位二进制 = 1 位八进制,4 位二进制 = 1 位十六进制
2. 信息编码
- BCD 码:8421 码(0-9 对应 4 位二进制 0000-1001)
- 字符编码:ASCII 码(1 字节,0-127 对应常用字符)
- 汉字编码:国标码(GB2312)、机内码(国标码最高位置 1)、输入码(拼音 / 五笔)、字模码(点阵表示)
3. 校验码(检错 / 纠错)
- 奇偶校验码:增 1 位校验位,使 1 的个数为奇 / 偶数
- 海明码:数据位 + 校验位(2ⁿ位置),可纠错 1 位
- CRC 码:模 2 运算生成余数作为校验码,检错能力强
4. 真值与机器数
- 真值:实际数值(如 + 123、-0.45)
- 机器数:符号数字化(0 正 1 负),含原码、反码、补码、移码
二、定点数的表示(熟练应用层)
1. 分类与格式
- 无符号数:全位表示数值,范围 0~2ⁿ-1
- 有符号数:
- 定点小数:小数点在符号位与数值位之间
- 定点整数:小数点在数值位最低位右侧
2. 机器码表示(字长 8 位为例)
| 码制 | 正数规则 | 负数规则 | 关键特点 |
|---|---|---|---|
| 原码 | 符号位 0 + 数值位 | 符号位 1 + 数值位绝对值 | 正负 0 不唯一 |
| 反码 | 符号位 0 + 数值位 | 符号位 1 + 数值位按位取反 | 正负 0 不唯一 |
| 补码 | 符号位 0 + 数值位 | 反码 + 1 | 唯一 0,加减统一为加法 |
| 移码 | 2ⁿ⁻¹+ 真值(n 为字长) | 2ⁿ⁻¹+ 真值 | 符号位与补码相反,用于阶码 |
3. 转换关系
- 补码→原码:正数不变,负数 "补码再求补"
- 原码→补码:负数 "按位取反 + 1"
- 移码与补码:符号位相反,数值位相同
三、浮点数的表示(简单应用层)
1. 基本格式
- 表达式:N = M×Rᴱ(M = 尾数,E = 阶码,R = 基数)
- 存储结构:阶符(Es)+ 阶码(E)+ 数符(Ms)+ 尾数(M)
2. 规格化要求
- 尾数满足 | 0.5|≤|M|<1(二进制),即尾数最高位为 1
- 规格化操作:左移尾数→阶码递减,右移尾数→阶码递增
3. IEEE 754 标准
- 单精度(32 位):符号位 1 位 + 阶码 8 位(偏置 127)+ 尾数 23 位(隐含整数 1)
- 双精度(64 位):符号位 1 位 + 阶码 11 位(偏置 1023)+ 尾数 52 位
- 真值公式:N = (-1)ˢ×(1.M)×2^(E - 偏置值)
四、常见问题与易混淆点
- 无符号数 vs 有符号数:无符号数无符号位,范围更大
- 定点数 vs 浮点数:定点数精度固定,浮点数范围更广
- 规格化判断:原码看尾数最高位是否为 1,补码看符号位与尾数最高位是否相反