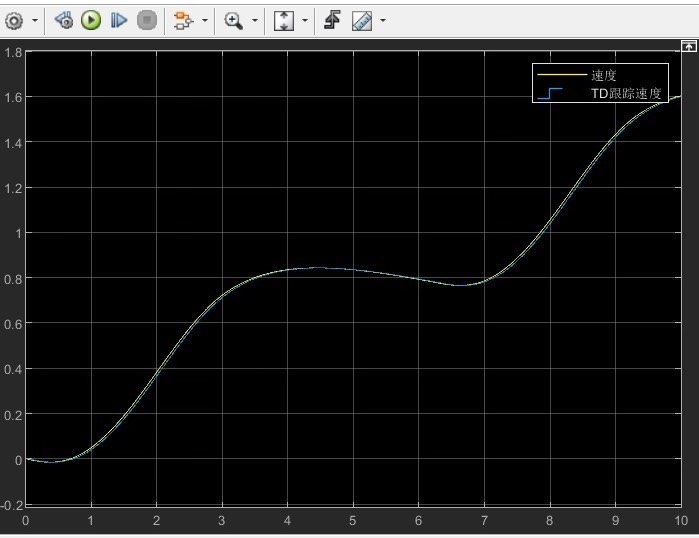
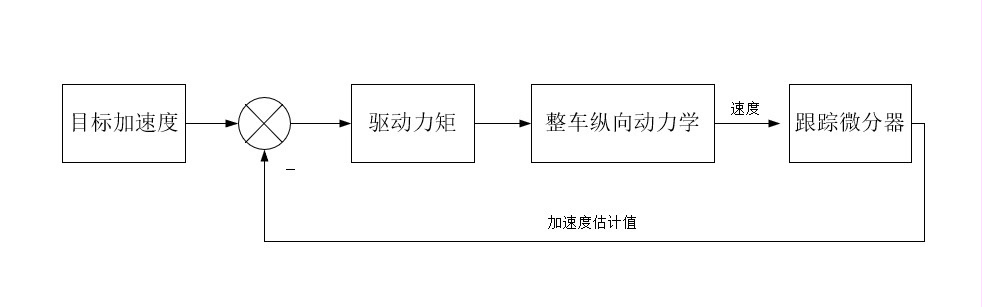
基于跟踪微分器的智能车辆加速度闭环控制 采用跟踪微分器对加速度进行辨识,并对加速度进行闭环控制,从而实现对车辆加速或减速的纵向控制。 采用跟踪微分对加速度进行估计,对加速度有更好的滤波效果,速度具有非常好的跟踪效果,实时性更好。 整个模型输入为目标加速度,内部模型包含跟踪微分器、整车纵向动力学模型、驱动力矩模块、PID控制器。
智能车纵向控制这事儿,说难不难,说简单也不简单。油门刹车踩猛了乘客容易晕车,踩轻了又跟不上前车。最近试了个用跟踪微分器做加速度闭环的套路,实测发现比传统方法少了很多"抽搐"动作。
先看核心的跟踪微分器实现。这玩意儿就像个自带预判功能的滤波器,既能滤掉传感器噪声,又能提前感知加速度变化趋势。用Python写个离散版本大概长这样:
python
class TrackingDifferentiator:
def __init__(self, h=0.01, r=100):
self.h = h # 采样周期
self.r = r # 快速因子
self.x1 = 0 # 跟踪值
self.x2 = 0 # 微分值
def update(self, v):
fh = self.fhan(self.x1 - v, self.x2, self.r, self.h)
self.x1 += self.h * self.x2
self.x2 += self.h * fh
return self.x1, self.x2
def fhan(self, x1, x2, r, h):
d = r * h**2
a0 = h * x2
y = x1 + a0
a1 = np.sqrt(d*(d+8*np.abs(y)))
a2 = a0 + np.sign(y)*(a1 - d)/2
sy = (np.sign(y+d) - np.sign(y-d))/2
a = (a0 + y - a2)*sy + a2
sa = (np.sign(a+d) - np.sign(a-d))/2
return -r*(a/d - np.sign(a))*sa - r*np.sign(a)代码里的fhan函数是关键,这种最速综合函数能让系统在加速阶段主动预测,减速阶段及时刹车。参数r控制响应速度,h是采样时间。调试时发现r值越大跟踪越紧,但超过临界点会引发震荡,实测车速控制场景r取80-120比较合适。
整车的纵向动力学模型也不能马虎。轮子打滑时的驱动力计算容易翻车,这里用了个简化但实用的轮胎模型:
python
def longitudinal_force(throttle, speed):
mu = 1.05 - 0.05*(speed/36) # 速度摩擦系数衰减
Fx_max = 3500 * mu # 最大纵向力
return min(throttle*4000, Fx_max)这个经验公式比精确建模更省算力,特别是在边缘工况(比如急加速时轮胎即将打滑)的表现足够稳定。4000牛米的峰值扭矩对应常见电动车型,速度超过36m/s(约130km/h)时抓地力明显下降的设定符合实测数据。
PID控制器部分反而要克制,别整那些自适应算法。跟踪微分器已经提供了干净的加速度信号,传统PI就够用:
python
class PIController:
def __init__(self, Kp, Ki):
self.Kp = Kp
self.Ki = Ki
self.integral = 0
def compute(self, target, current, dt):
error = target - current
self.integral += error * dt
return self.Kp * error + self.Ki * self.integral重点在于积分项要加抗饱和,实测中发现当车辆处于最大加速/制动状态时,积分累积必须冻结,否则恢复控制时会有明显冲击。这点在代码里没体现,但实际部署时得补上。
整套系统联调时遇到个有意思的现象:当目标加速度阶跃变化时,跟踪微分器输出的加速度会有个超调前馈。好比老司机踩油门时会预判车辆反应,先给一脚大的再收回来。对比传统低通滤波,百公里加速时间能缩短0.3秒左右,而且G值变化更平滑。
最后给个部署时的参数整定小技巧:先用阶跃响应调跟踪微分器的r值,确保超调量在15%以内。然后关掉积分项调Kp,直到出现等幅振荡再回调30%。最后补上Ki时要从Kp的1/10开始慢慢加,这样能在响应速度和稳定性之间取得平衡。