【算法】二分图理论知识和判断方法

二分图详解
- [Part 1.1 二分图的理论知识](#Part 1.1 二分图的理论知识)
  - [Part 1.1.1 什么是二分图](#Part 1.1.1 什么是二分图)
  - [Part 1.1.2 二分图的例子](#Part 1.1.2 二分图的例子)
- [Part 1.2 二分图的判定](#Part 1.2 二分图的判定)
  - [Part 1.2.1 染色算法时空复杂度](#Part 1.2.1 染色算法时空复杂度)
  - [Part 1.2.2 算法理论](#Part 1.2.2 算法理论)
  - [Part 1.2.3 代码实现](#Part 1.2.3 代码实现)
Update

二分图详解

二分图在算法竞赛中是一个非常常见的东西, 学会这个东西在解决一些常见的问题是会非常有用的。

Part 1.1 二分图的理论知识

下面将介绍二分图的理论知识，如果不喜欢可以跳出。

Part 1.1.1 什么是二分图

二分图的定义: \text{二分图的定义:} 二分图的定义:

这个图可以被分成两个部分 \text{这个图可以被分成两个部分} 这个图可以被分成两个部分
每一条边的两个端点在不同的部分 \text{每一条边的两个端点在不同的部分} 每一条边的两个端点在不同的部分

Part 1.1.2 二分图的例子

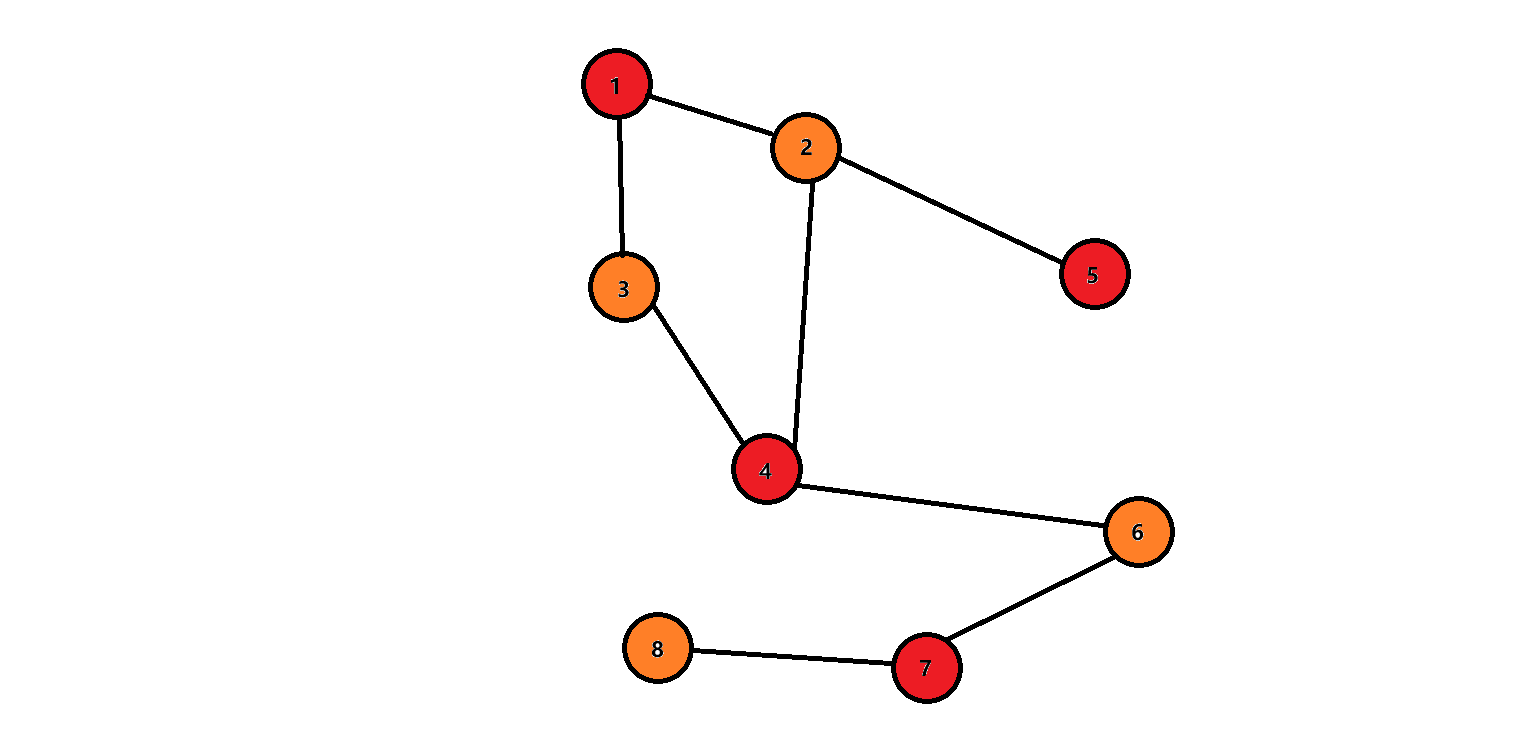
上面的图就是一个二分图，它满足:

红色的点为 1 1 1 个集合，橙色的点为 1 1 1 个集合。
而且每一条边连接的两个位置的点都是处于不同的集合

再看下面的一张图

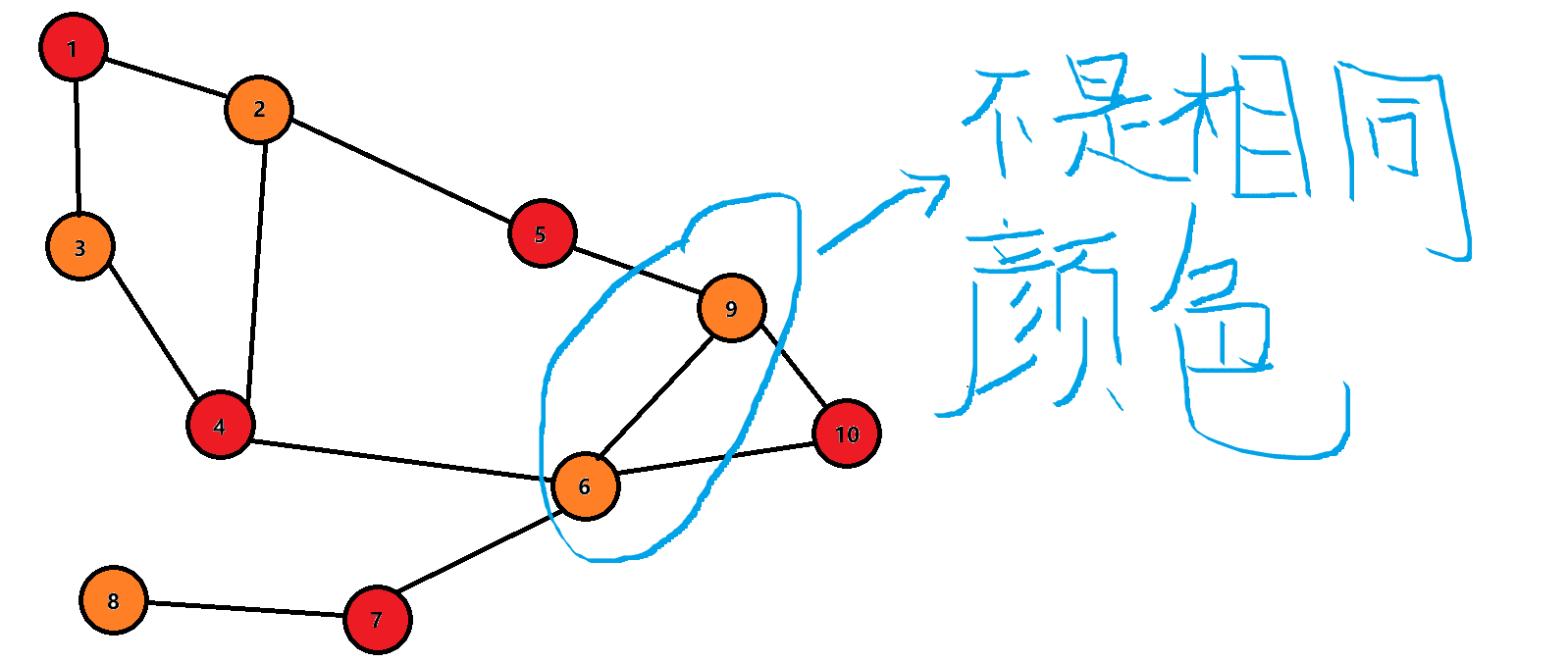
图上标注的很清楚，节点 9 9 9 和节点 6 6 6 的颜色是相同的，所以不满足二分图的条件

Part 1.2 \text{Part 1.2} Part 1.2 二分图的判定

这个东西是一个重点，也叫二分图染色(Bipartite Graph Coloring) \text{二分图染色(Bipartite Graph Coloring)} 二分图染色(Bipartite Graph Coloring)

Part 1.2.1 染色算法时空复杂度

其中 N N N 表示点数, M M M 表示边数

使用邻接矩阵存图，时间复杂度和空间复杂度均为 O ( N 2 ) O(N^2) O(N2). (一般用于稠密图, 因为此时 M = N 2 M = N^2 M=N2)
使用 vector \text{vector} vector 或邻接表存图，时间复杂度和空间复杂度均为 O ( N + M ) O(N + M) O(N+M).
在稀疏图上面， M M M 和 N N N 同阶.
在稠密图上， M M M 和 N 2 N^2 N2 同阶

但是一般采用邻接表存图.

Part 1.2.2 算法理论

很简单，对每个点进行 dfs, 给每个出边染上相反的颜色即可，如果出现矛盾，就不是二分图。

下面是动图，用于理解。

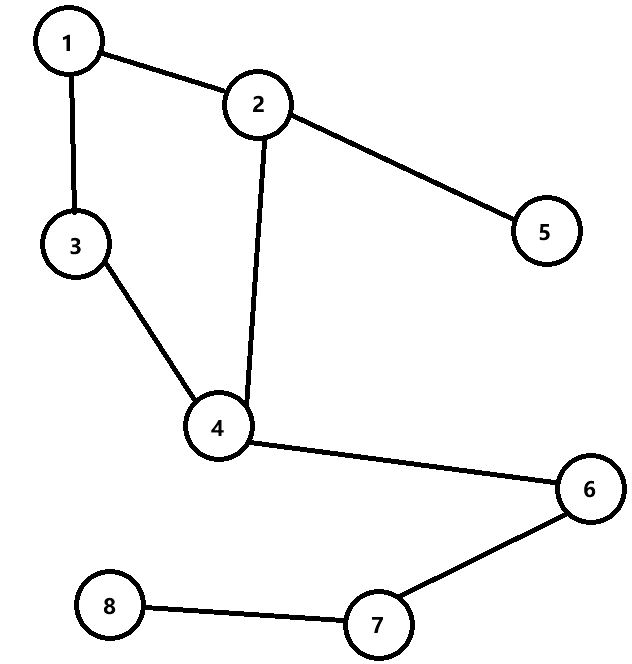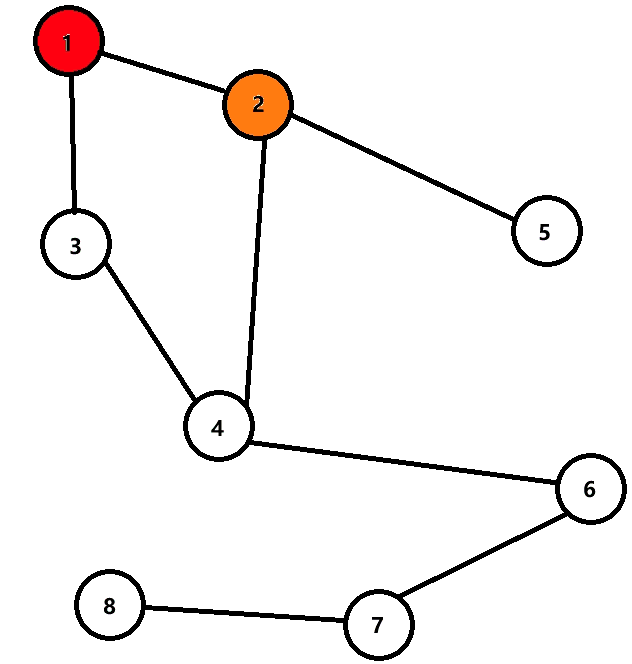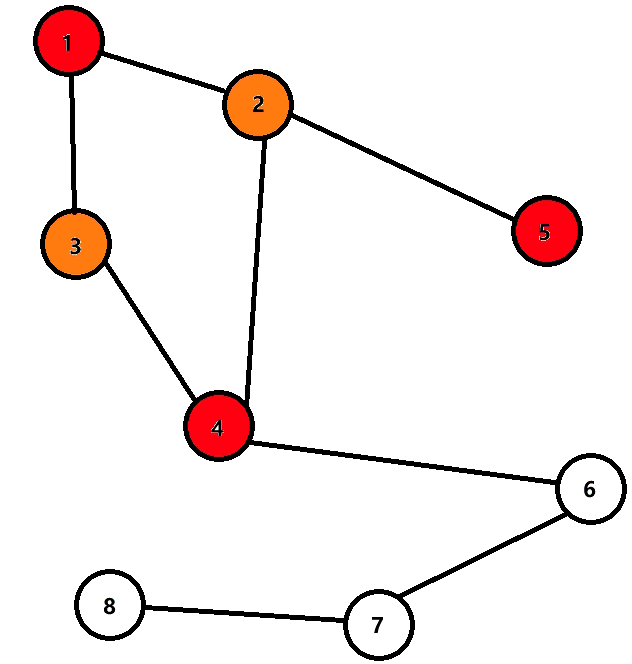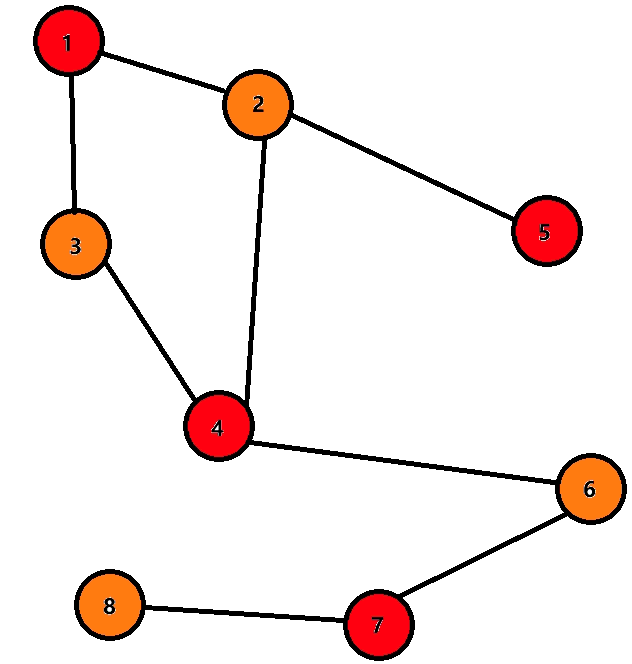
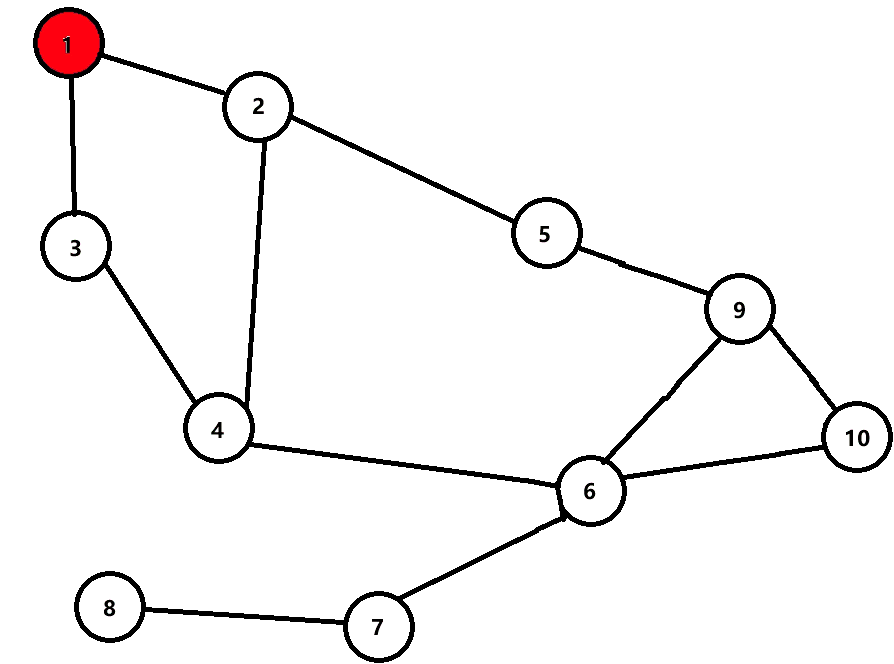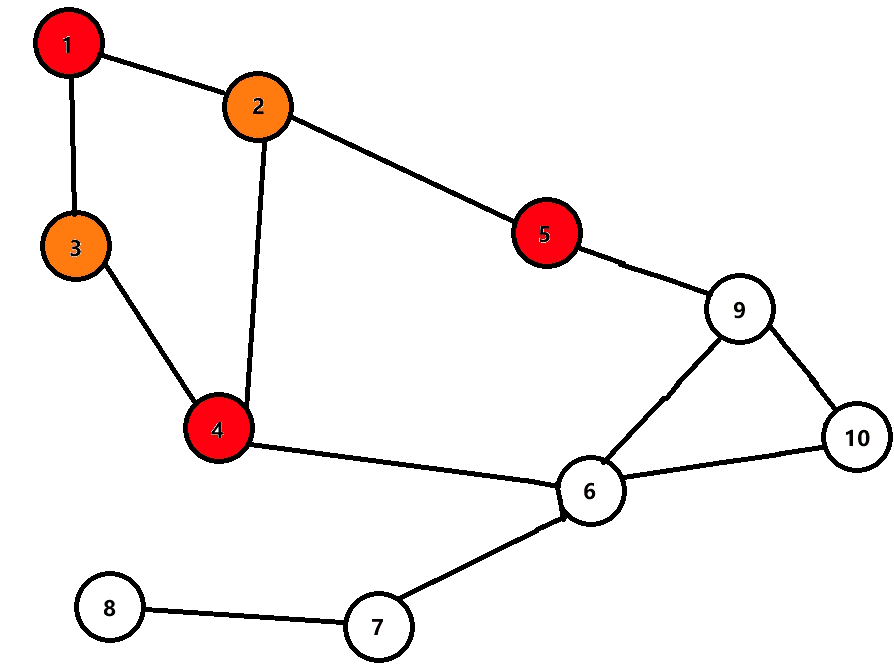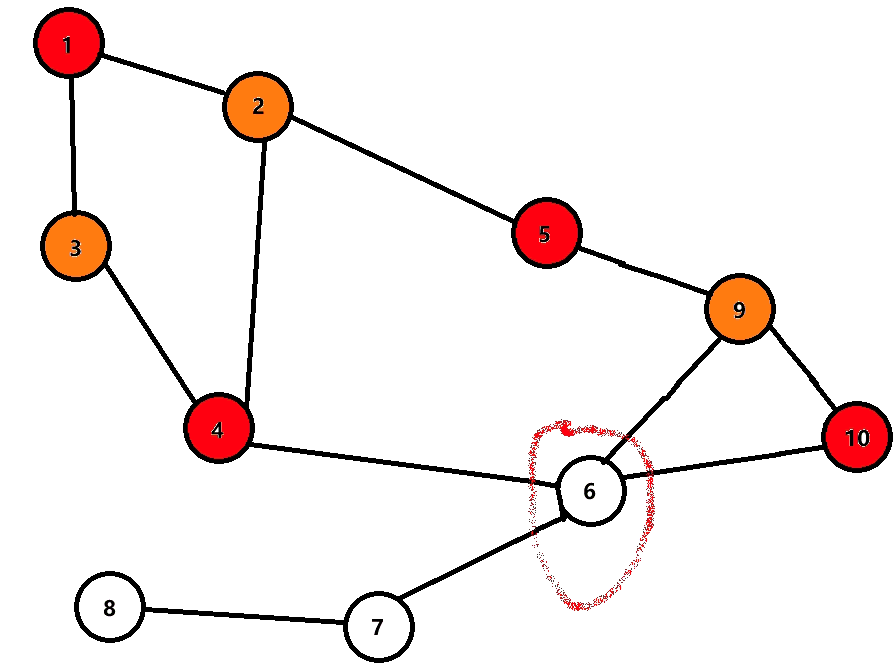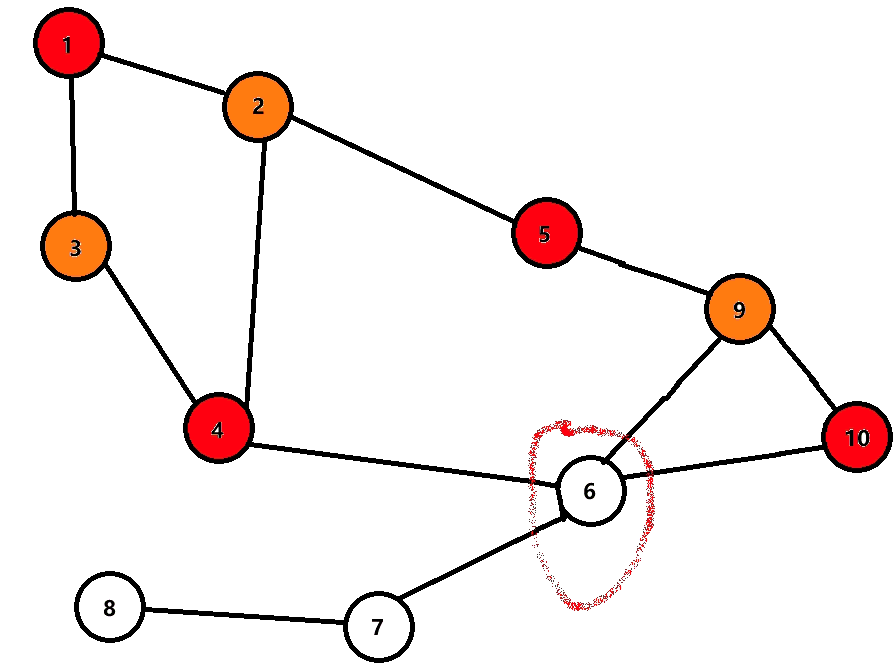
发现染色部分进行到 6 6 6 时出现矛盾，所以不是二分图。

Part 1.2.3 代码实现

cpp 复制代码

#include <bits/stdc++.h>

using namespace std;

const int MAXN = 10005;

vector<int> G[MAXN];

int color[MAXN];

bool DFS(int u, int col) {
    color[u] = col;
    for (int v : G[u]) {
        if (color[v] == -1) {
            if (!DFS(v, !col)) return false;
        }
        if (color[v] == col) return false;
    }
    return true;
}

int main() {
    int N, M;
    // 假设输入 N M 和边，这里省略输入部分
    memset(color, -1, sizeof(color));
    bool isBipartite = true;
    for (int i = 1; i <= N; i++) {
        if (color[i] == -1) {
            if (!DFS(i, 0)) {
                isBipartite = false;
                break;
            }
        }
    }
    if (isBipartite) {
        printf("Yes");
    } else {
        printf("No");
    }
    return 0;
}

如果出现问题，可以在评论区好好讨论

Update \text{Update} Update

创建时间 2025.12.24'

【算法】 二分图理论知识和判断方法

目录