逻辑回归实战进阶：交叉验证与采样技术破解数据痛点（二）

在机器学习二分类任务中，数据不平衡是最常见的实战痛点之一 ------ 比如信用卡欺诈检测中欺诈样本仅占 0.17%、金融风控中违约用户不足 5%、医疗诊断中阳性病例占比极低。逻辑回归作为经典的线性分类算法，对数据分布尤为敏感，若直接用不平衡数据训练，模型会天然偏向多数类（正常样本），导致少数类（核心关注样本）的识别率极低，看似高准确率的模型，实际落地毫无价值。

而过采样（Over-Sampling）和下采样（Under-Sampling），正是解决数据不平衡的两大核心手段：过采样通过增加少数类样本数量 实现数据平衡，下采样通过减少多数类样本数量实现数据平衡。本文将从原理出发，拆解两种采样方法的核心逻辑、优缺点及实战要点，结合可直接运行的代码框架（适配你自带的实战例子），讲清逻辑回归中如何正确使用过采样和下采样，让模型精准捕捉少数类特征。

一、先明确：什么是数据不平衡？为何会影响逻辑回归？

1. 数据不平衡的定义

简单来说，数据不平衡指二分类任务中，正负类样本数量比例悬殊，行业内通常认为比例超过 1:10即为显著不平衡，极端场景下比例甚至会达到 1:1000（如信用卡信誉检测）。

我们以经典的信用卡信誉检测数据集（creditcard.csv） 为例：总样本 284807 条，正常交易（负类，Class=0）284315 条，欺诈交易（正类，Class=1）仅 492 条，正负类比例约 578:1，属于极度不平衡数据------ 这也是本次实战的核心测试数据。

2. 数据不平衡对逻辑回归的致命影响

在不平衡数据中，即使模型无脑预测所有样本为多数类，也能得到极高的准确率（比如信用卡欺诈检测中，直接预测所有交易为正常，准确率可达 99.828%），此时模型会完全忽略少数类的特征规律，导致少数类的召回率、F1 值趋近于 0。

更关键的是，逻辑回归是线性模型，特征权重的学习依赖于样本的分布特征，不平衡的数据会让模型学到的权重偏向多数类，最终得到的分类超平面严重失衡，无法有效区分少数类样本。

二、核心解法一：下采样（Under-Sampling）------ 对多数类做 "减法"

下采样是解决数据不平衡的极简思路，核心是通过减少多数类样本数量，让正负类样本数量趋于平衡，让模型能平等学习两类样本的特征。因其操作简单、训练速度快，成为很多新手处理不平衡数据的首选。

1. 下采样的核心原理

下采样的逻辑非常直观，核心三步：

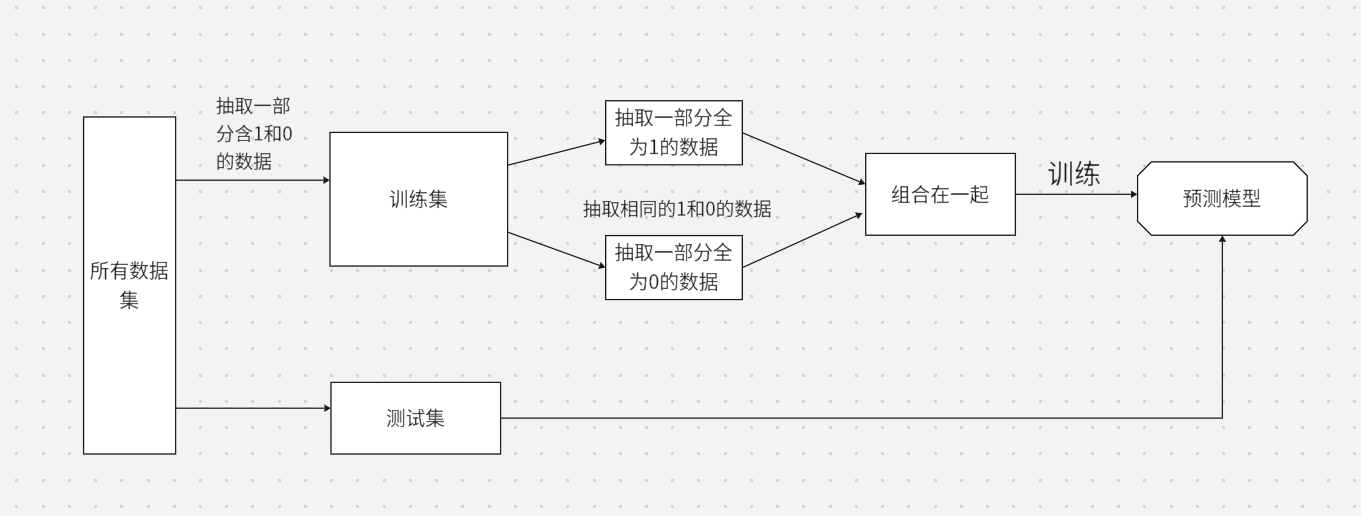
1. 从多数类（负类） 样本中，随机抽取与少数类样本数量相等或接近的样本；
2. 将抽取的多数类样本，与全部少数类（正类） 样本合并，构建新的平衡训练集；
3. 用平衡训练集训练逻辑回归模型。

举个例子：信用卡信誉检测中，少数类（失信）有 492 条，从多数类（正常）的 284315 条中随机抽取 492 条，合并后得到 984 条平衡样本，正负类比例 1:1，用这部分数据训练逻辑回归。

2. 下采样的优缺点（实战必看）

实例（信用卡信誉检测 ）：

import pandas as pd
import numpy as np
data = pd.read_csv('creditcard.csv')
from sklearn.preprocessing import StandardScaler   # z标准换的数
scaler = StandardScaler()  # 实例化标准化对象scaLer
data['Amount'] = scaler.fit_transform(data[['Amount']])  # 将计算后的标准差存入data中
data = data.drop(['Time'], axis=1)  # 删除Time列的内容，axis为1表示列

from sklearn.model_selection import train_test_split  # 专门用来对数据集进行切分的函数
X_whole = data.drop('Class', axis=1)  # 删除cLass列，其余数据作为特征集
y_whole = data.Class  # class列作为标签Label标注)
x_train_w, x_test_w, y_train_w, y_test_w =\
  train_test_split(X_whole, y_whole, test_size=0.2, random_state=0)  # 数据集进行切分

# 组合训练集的标签和特征
x_train_w['Class'] = y_train_w
data_train = x_train_w

'''下采样解决样本不均衡的问题'''
position_eg = data_train[data_train['Class'] == 0]  # 获取到所有标签为0的数据
negative_eg = data_train[data_train['Class'] == 1]  # 获取到所有标签为1的数据
position_eg = position_eg.sample(len(negative_eg))  # sample表示随机从参数里面选择数据
data_c = pd.concat([position_eg, negative_eg])  # 将两个数据组合在一起

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score
'''训练集试用下采样数据，测试使用原始数据进行预测'''
X = data_c.drop('Class', axis=1)  # 对data_c数据进行划分
y = data_c.Class
# 交叉验证
scores = []
c_param_range = [0.01, 0.1, 1, 10, 100]
for i in c_param_range:
    lr = LogisticRegression(C=i, penalty='l2', solver='lbfgs', max_iter=1000)
    score = cross_val_score(lr, x_train_w, y_train_w, cv=5, scoring='recall')
    score_mean = sum(score)/len(score)
    scores.append(score_mean)
    print(score_mean)

best_c = c_param_range[np.argmax(scores)]  # 寻找到scores中最大值得对应的C参数


'''建立最优模型'''
lr = LogisticRegression(C=best_c, penalty='l2', max_iter=1000)
lr.fit(X, y)
from sklearn import metrics

'''小训练集数据进行自测'''
train_predicted = lr.predict(X)
print(metrics.classification_report(y, train_predicted))

'''测试集数据进行测试'''
test_predicted = lr.predict(x_test_w)
print(metrics.classification_report(y_test_w, test_predicted, digits=6))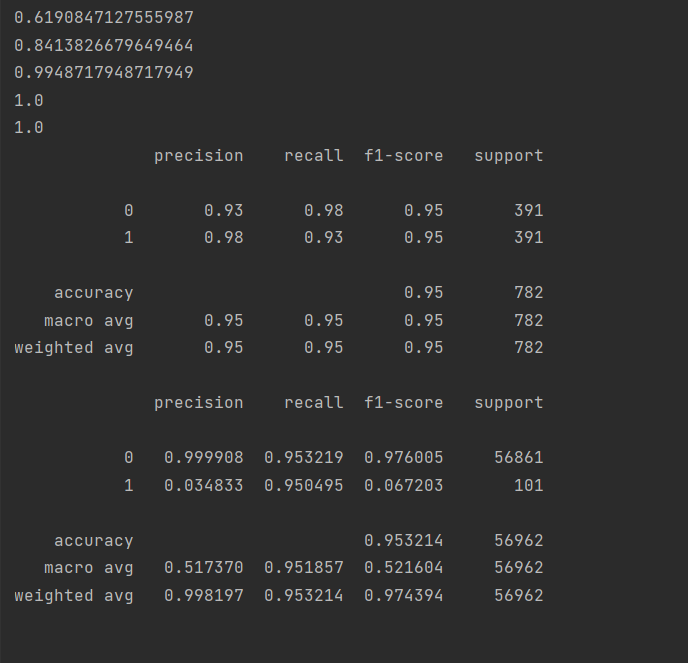

优点

• 操作简单：无需复杂的算法实现，仅需随机抽样即可，代码易上手；
• 训练效率高：减少了样本数量，逻辑回归的训练速度大幅提升，适合大数据集快速验证；
• 无数据冗余：仅使用原始样本，不会引入合成数据，避免合成样本带来的特征偏差。

缺点（核心痛点）

• 丢失大量有效信息：随机抽取会舍弃绝大多数多数类样本，可能丢失多数类的重要特征规律，导致模型对多数类的预测能力下降；
• 过拟合风险：若抽取的多数类样本无法代表整体多数类的分布，或包含较多噪声，模型会过拟合于抽样后的小样本，泛化能力变差；
• 效果上限低：仅适用于多数类样本特征重复度高、噪声多的场景，对多数类特征分布复杂的场景，效果远不如过采样。

三、核心解法二：过采样（Over-Sampling）------ 对少数类做 "加法"

与下采样的 "减法" 思路相反，过采样是通过增加少数类样本数量 实现数据平衡，也是逻辑回归处理不平衡数据的主流选择。因其不会丢失任何原始样本信息，能最大程度保留数据的特征规律，适配绝大多数不平衡数据场景。

1. 过采样的两种核心方法

过采样主要分为简单随机过采样 和SMOTE 合成过采样，其中 SMOTE 是实战中的首选，彻底解决了简单过采样的过拟合问题。

（1）简单随机过采样

核心原理

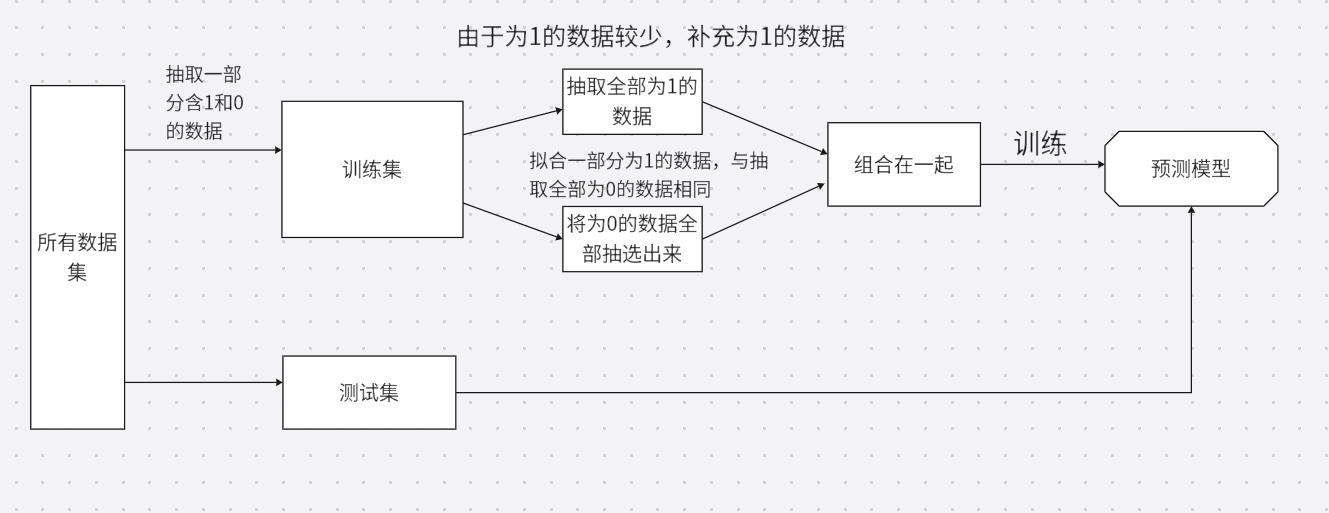
从少数类样本中随机重复抽取样本，直到少数类样本数量与多数类样本数量接近。比如信用卡信誉检测中，从 492 条正常样本中随机重复抽取 283823 条，最终少数类样本达到 284315 条，与多数类比例 1:1。

优缺点

• 优点：操作比下采样更简单，一行代码即可实现；
• 缺点：严重的过拟合风险------ 重复抽取会导致少数类特征高度冗余，模型会过度学习这些重复样本，在测试集上的泛化能力极差。

（2）SMOTE 合成过采样

SMOTE（Synthetic Minority Oversampling Technique）即合成少数类过采样技术 ，是目前工业界处理不平衡数据的主流算法，核心是生成新的、有代表性的少数类合成样本，而非简单重复。、

但是需要安装imbalanced-learn库才能使用

在命令提示符输入：

pip install imbalanced-learn -i https://pypi.tuna.tsinghua.edu.cn/simple

1. 对每个少数类样本，在特征空间中找到其k 个最近邻的少数类样本（k 通常取 5，可自定义）；
2. 随机选择其中 1 个邻域样本，在原样本和邻域样本的特征向量之间构建连线；
3. 在连线上随机生成新的样本（新样本特征值 = 原样本特征值 + 随机系数 ×(邻域样本特征值 - 原样本特征值)，随机系数∈[0,1]）；
4. 重复上述过程，直到少数类样本数量达到目标，与多数类实现平衡。

实例（信用卡信誉检测 ）：

import time

import pandas as pd
import numpy as np
data = pd.read_csv('creditcard.csv')
from sklearn.preprocessing import StandardScaler   # z标准换的数
scaler = StandardScaler()  # 实例化标准化对象scaLer
data['Amount'] = scaler.fit_transform(data[['Amount']])  # 将计算后的标准差存入data中
data = data.drop(['Time'], axis=1)  # 删除Time列的内容，axis为1表示列

from sklearn.model_selection import train_test_split  # 专门用来对数据集进行切分的函数
X_whole = data.drop('Class', axis=1)  # 删除cLass列，其余数据作为特征集
y_whole = data.Class  # class列作为标签Label标注)
x_train_w, x_test_w, y_train_w, y_test_w =\
  train_test_split(X_whole, y_whole, test_size=0.2, random_state=0)  # 数据集进行切分

'''进行过采样操作'''
from imblearn.over_sampling import SMOTE
oversampler = SMOTE(random_state=0)  # 保证数据拟合效果，随机种子
os_x_train, os_y_train = oversampler.fit_resample(x_train_w, y_train_w)  # 人工拟合数据

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score
# 交叉验证
scores = []
c_param_range = [0.01, 0.1, 1, 10, 100]
z = 1
for i in c_param_range:
    start_time = time.time()
    lr = LogisticRegression(C=i, penalty='l2', solver='lbfgs', max_iter=1000)
    score = cross_val_score(lr, x_train_w, y_train_w, cv=5, scoring='recall')
    score_mean = sum(score)/len(score)
    scores.append(score_mean)
    end_time = time.time()
    print("recall:{}".format(score_mean))
    z += 1

best_c = c_param_range[np.argmax(scores)]# 寻找到scores中最大值得对应的C参数

print("最优惩罚因子:{}".format(best_c))
lr = LogisticRegression(C=best_c, penalty='l2', solver='lbfgs', max_iter=1000)
lr.fit(os_x_train, os_y_train)

from sklearn import metrics
train_predicted = lr.predict(os_x_train)
print(metrics.classification_report(os_y_train, train_predicted))

test_predicted = lr.predict(x_test_w)
print(metrics.classification_report(y_test_w, test_predicted, digits=6))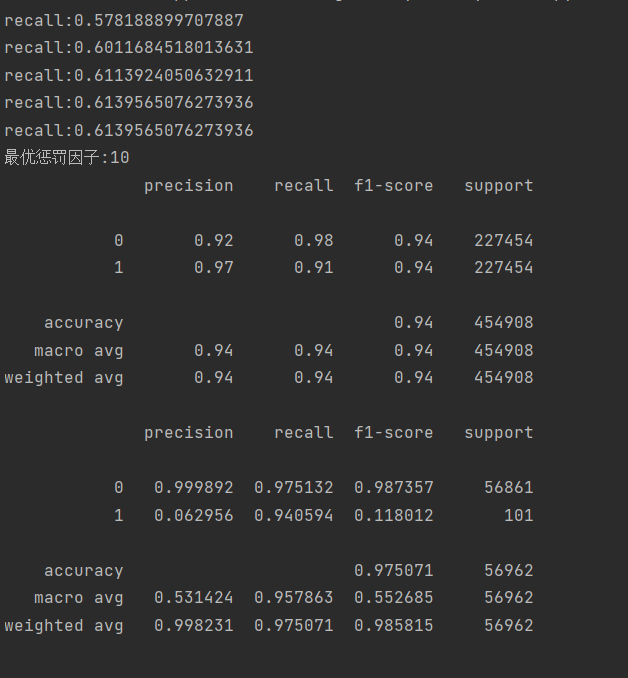

优缺点

• 优点：生成的是全新的样本，无特征冗余，有效避免过拟合；不丢失任何原始数据信息，能最大程度保留特征规律；适配绝大多数不平衡数据场景，效果稳定；
• 缺点：计算量比简单过采样大（需计算样本间的距离）；对少数类中的异常值敏感------ 若少数类样本包含异常值，会生成不合理的合成样本，影响模型效果；对高维数据，邻域样本的计算效率会下降。

四、总结

过采样和下采样看似简单，但真正的实战价值在于 "正确使用"------ 遵循实战原则，结合业务需求选择合适的方法，再搭配逻辑回归的算法优化，即使是经典的线性模型，也能在高度不平衡的实战场景中，实现精准的分类效果。你可以将本文的代码框架直接替换为自己的实战例子，调整参数后即可快速落地，动手实操才是掌握的关键！