【IC】timeloop：AI Core量化仿真

文章概览

这是一篇计算机体系结构领域的经典学术论文，题目叫《Timeloop: A Systematic Approach to DNN Accelerator Evaluation》。

虽然这是专业的科研论文，但其核心逻辑其实非常贴近生活，我将用一个**"超级工厂与物流管理"**的类比来拆解这篇文章。

这篇文章主要解决了一个问题：如何设计和评估专门用来跑人工智能（AI）的芯片？

第一部分：背景与问题（为什么要写这篇文章？）

1. 现在的困境：AI 芯片太难设计了

现在的深度神经网络（DNN）非常火，用在自动驾驶、语音识别等领域。为了让这些 AI 跑得快又省电，工程师们设计了专门的硬件，叫DNN 加速器（你可以理解为专门用于 AI 计算的"超级工厂"）。

但是，设计这种工厂有个大难题：

硬件很复杂： 里面有成千上万个计算单元（工人）和不同层级的存储器（仓库）。
不仅看硬件，更看"调度"： 就算你有了最好的工厂，如果物流调度一团糟（比如让工人频繁跑远路去拿零件，或者工人闲着没事干），效率也会极低。在芯片里，这种"调度方式"被称为Mapping（映射） 。

2. 核心痛点：同样的硬件，不同的"调度"，差距巨大

文章做了一个实验，在一个类似英伟达 NVDLA 的芯片上跑同一个任务，尝试了 48 万种不同的"调度方式"（Mappings）。

结果发现：最好和最差的调度方式，能耗相差了 19 倍！。
这意味着：如果你不懂怎么优化调度，你设计的芯片可能只能发挥出 5% 的实力。

3. 缺乏工具

以前，设计师主要靠经验（像"艺术"而非"科学"）来设计芯片。缺乏一个通用的工具来告诉他们："在这个硬件上，用哪种调度方式是绝对最好的？"。

这就是 Timeloop 诞生的原因：它是一个能自动寻找最佳调度方案，并评估芯片性能的模拟器 。

第二部分：Timeloop 是如何工作的？（核心原理）

你可以把 Timeloop 想象成一个**"超级军师"或"智能调度系统"**。它的工作流程分为三个步骤：

1. 输入（告诉系统你要干什么）

Timeloop 需要你提供三样东西：

任务书 (Workload)： 你要算的 AI 模型是什么样子的？（比如卷积层的尺寸、输入输出通道数）。文章中把这看作是一层层的循环嵌套（Loop Nest）。
硬件图纸 (Architecture)： 你的工厂长什么样？有多少计算单元？内存有多大？数据怎么传输？。
规则限制 (Constraints)： 有什么必须要遵守的死规定？（比如某些数据必须存放在特定的地方）。

2. 核心引擎：映射器 (Mapper)

这是 Timeloop 最聪明的地方。它会生成一个**"映射空间 (Mapspace)"**，里面包含了所有可能的调度方案。

由于可能的方案太多了（天文数字），通过穷举是不可能的。
Timeloop 会在这个空间里进行搜索，找到那个能耗最低、速度最快的"最佳映射" 。

3. 评估模型 (Model)

找到了一个调度方案后，怎么知道它好不好呢？Timeloop 有一个快速计算模型：

不是慢速回放： 它不像传统的模拟器那样一秒一秒地模拟（太慢了）。
而是数学计算： 它通过数学公式计算数据的"平铺 (Tiling)"方式。简单说，它计算数据在不同仓库（缓存）之间移动了多少次，工人（计算单元）计算了多少次。
算出代价： 移动一次数据消耗多少电，计算一次消耗多少电，加起来就是总能耗。

第三部分：验证与发现（它真的准吗？）

作者不仅造出了工具，还证明了它很好用。

1. 验证准确性

作者拿 Timeloop 的预测结果，和两个真实存在的著名 AI 芯片（NVDLA 和 Eyeriss）的实测数据进行了对比。

结果： 预测的准确率非常高，对于绝大多数任务，误差都在很小的范围内。这证明高中生做物理题用的公式法（Timeloop 的数学模型）比笨拙地做实验（逐周期模拟）既快又准。

2. 有趣的案例研究 (Case Studies)

利用 Timeloop，作者发现了一些反直觉的现象，这对芯片设计师很有启发：

案例 A：技术升级，调度也要变
这就好比你的工厂从"人力搬运"升级到了"机器臂搬运"。
作者发现，当芯片制造工艺从 65nm（老工艺）升级到 16nm（新工艺）时，原来的"最佳调度方案"变得不再是最佳了。
如果你在新芯片上还用老一套调度方法，能耗会浪费 22% 。
案例 B：存储器的设计很关键
作者研究了 Eyeriss 芯片的存储结构，发现如果把一个大的共享仓库（寄存器堆），改成几个小的专用仓库（分别存输入、权重、输出），能耗可以降低 40% 以上。
这说明：数据流（Dataflow）和存储层次的协同设计是省电的关键 。
案例 C：没有"万能"的芯片
作者对比了三种不同的芯片架构。发现没有谁是全能的。
有的芯片在通道数多的时候效率高，有的芯片在通道数少的时候效率低（因为工人闲置了）。

第四部分：总结（这篇文章的贡献）

作为一名高中生，你只需要记住这篇文章解决了什么核心矛盾：

问题： AI 芯片设计很复杂，且极其依赖软件层面的"调度"（Mapping）。
方法： 作者开发了 Timeloop，这是一个能自动搜索最佳调度方案、并快速评估硬件性能的工具。
意义： 它让芯片设计从这就"凭感觉的艺术"变成了"精确计算的科学" 。它能帮助工程师在造出芯片之前，就知道这个芯片好不好，以及该怎么用才能发挥最大威力。

一句话总结： 这篇文章提出了一个"智能模拟器"，它能帮工程师在设计 AI 芯片时，自动找到让数据搬运最少、计算最快的最佳方案。

学习路径

想要开发类似 Timeloop 这样的工具，不仅需要理解计算机体系结构，还需要掌握编译原理中的循环优化和设计空间搜索算法。

这篇论文的核心在于解决了一个关键痛点：同样的硬件架构，如果数据的调度（Mapping）方式不同，性能和能耗可能会有天壤之别 。

为了让你能够深入理解并最终具备开发能力，我们需要将这篇论文拆解为几个关键模块来逐个攻破。

我们可以从以下三个切入点开始，请告诉我你想先从哪里入手：

宏观视角：为什么要"搜索"？ (The Why)

我们将深入探讨论文的动机（Motivation）部分。重点理解为什么作者认为设计硬件时必须同时考虑"映射器"（Mapper），以及图 1 中提到的 19 倍能耗差距是如何产生的。这对于理解工具的核心价值至关重要。
核心抽象：如何描述硬件和负载？ (The Inputs)

如果你想写代码，首先需要定义数据结构。我们将学习 Timeloop 是如何用"循环嵌套"（Loop Nest）来抽象神经网络层，以及如何用树状结构来描述硬件的存储层次。这是构建工具的基石。
内部引擎：映射与评估模型 (The How)

这是最硬核的部分。我们将研究它如何构建"映射空间"（Mapspace），以及它的数学模型（Tile Analysis）是如何在不进行逐周期模拟的情况下，快速计算出性能和能耗的。这是工具的核心算法。

第一部分：宏观视角

没问题，我们先从**宏观视角（Motivation）**开始。这部分是理解整个工具存在意义的关键。

1. 为什么"硬件好"还不够？

论文在开头提出了一个非常有意思的观点：目前的 AI 芯片设计更像是一门"艺术"，而不是"科学" 。意思是很多时候设计师是凭感觉在设计，而不是凭精确的计算。

作者为了证明这一点，做了一个实验（论文中的 Figure 1）：

硬件不变：使用一个类似 NVDLA（英伟达的开源加速器）的芯片架构。
任务不变：运行一个卷积神经网络层（VGG_conv3_2）。
变量：改变"调度方式"（也就是 Mapping）。

结果非常惊人：在找到的 48 万种不同的"调度方式"中，最差的方案比最好的方案，能耗高出了 19 倍 ！

2. 想象一个"超级厨房"

为了理解这 19 倍 的差距是从哪来的，我们可以把芯片想象成一个超级厨房：

硬件（Architecture）：就是你的厨房设施（有 100 个灶台，1 个大冰箱，10 个小柜子）。
任务（Workload）：你要做一道非常复杂的菜（比如"宫保鸡丁"做 1000 份）。
映射（Mapping/调度）：就是**"怎么安排厨师干活"**的计划表。

在这个类比中，"调度"（Mapping）决定了效率：

差的调度（高能耗）：厨师切一个洋葱，跑去大冰箱拿一次；切完再跑回去拿蒜；再跑回去拿姜。
结果：大家都在路上跑来跑去，体力（电能）全浪费在路上了。
好的调度（低能耗）：厨师一次性从大冰箱把所有洋葱、蒜、姜都拿来，放在手边的小柜子里，切完了再炒。
结果：少跑路，多干活。

让我们来思考一下

在芯片里，"跑路"对应的就是数据搬运 （从内存读取数据），而"切菜"对应的是计算（加法、乘法）。

根据上面的厨房类比，你觉得在 AI 芯片中，是"计算"比较费电，还是"搬运数据"比较费电？ 为什么差的调度会浪费那么多能量？

在计算机芯片的世界里，搬运数据 （物流）的能耗通常是计算（切菜）能耗的几十倍甚至上百倍！

让我们回到"超级厨房"

计算（MAC 操作）：就像厨师切一下菜。这只需要动动手指，消耗的能量很小（比如 1 焦耳）。
从内存取数据（DRAM Access）：就像厨师跑到几公里外的仓库去取菜。这消耗的能量极其巨大（比如 200 焦耳）。
从缓存取数据（Buffer Access）：就像从手边的柜子里拿菜。虽然比跑仓库省电，但也比切菜费电得多。

为什么调度（Mapping）这么重要？

正如论文中提到的，有些调度方案虽然减少了去大仓库（DRAM）的次数，但如果没有优化好手边柜子（Buffer）的使用，能耗依然会很高。

现在的关键问题来了：

既然"跑路"（搬运数据）比"干活"（计算）贵这么多，如果有一个数据（比如一个卷积核的权重）需要被使用 100 次，为了省电，我们应该在这个数据第一次被搬运到"手边"时，立刻做什么操作？

没错！把它放在离计算单元最近的"手边"（比如 寄存器文件 Register File）里是第一步。

但是，仅仅"放在那"还不够。

回到我们的厨房比喻：

如果厨师好不容易跑去仓库把洋葱拿回来，放在手边，为了最极致地省力（省电），他应该：

切一刀，然后把洋葱放回仓库，下次要用再跑去拿。
趁着洋葱在手边，一口气把所有需要洋葱的菜全切出来，然后再也不用去仓库拿洋葱了。

肯定是 2，对吧？在芯片设计里，这叫做 数据复用 (Data Reuse) 。Timeloop 这篇文章的核心观点之一就是：不同的"调度"方式，决定了你能把数据复用做得多好。

引导问题：

这就引出了 Timeloop 最核心的搜索目标。既然搬运一次数据的代价那么大（比如 200 焦耳），而计算一次很便宜（1 焦耳）。为了让平均每次计算的能耗（Energy/MAC）变低，我们需要在数据被"扔掉"之前，尽可能多做计算还是少做计算？

为了让那昂贵的"跑路费"（比如 200 焦耳）变得划算，我们必须在把数据从"手边"扔掉之前，尽可能压榨它的价值，让它参与成百上千次计算。

在芯片设计里，这被称为 数据复用 (Data Reuse) 。这也是所有 AI 加速器省电的核心秘诀。

既然道理这么简单，为什么还这么难？

这正是 Timeloop 这篇文章要解决的核心痛点。虽然原则是"多复用"，但实际操作起来非常复杂，因为变量太多了：

"菜谱"总在变（Workload）：AI 模型里的每一层都不一样。有的层通道数多（洋葱多），有的层特征图大（面粉多）。适合第一层的调度方式，到了第二层可能就是灾难。
"厨房"各不同（Architecture）：不同的芯片，缓存大小（柜子容量）和连接方式都不同。
组合爆炸 ：正如论文中那个惊人的数据，仅仅是在一个硬件上跑一个层，就有 480,000 种 合法的调度方式（Mappings）。

这意味着，这是一个巨大的迷宫，而"最佳出口"藏在几十万条死胡同里。

思考时间

面对这 48 万种可能性，而且我们知道最差和最好的方案能耗差了 19 倍，你觉得如果单纯靠人类工程师的"经验"或"直觉"来设计芯片和写调度程序，最大的风险是什么？

面对 48 万种可能性，人类大脑是无法处理的。如果没有工具辅助，设计师很可能只凭经验选了一个"自以为不错"的调度方案，结果可能比最优方案多耗好几倍的电。

这就导致了一个严重的后果：不仅软件跑得慢，甚至可能误导硬件设计。 比如，你以为是芯片设计得不好，其实只是因为没有找到正确的使用方法（调度）。

Timeloop 的核心价值就在于：它用"自动化搜索"替代了"人工猜测"。

第二部分：核心抽象（如何告诉工具你要做什么？）

既然明白了为什么要搜 ，下一步就是怎么搜。

要想让计算机帮我们干活，我们得先用它听得懂的语言，把"任务"和"硬件"描述清楚。这也是你想开发类似工具的第一步：定义数据结构。

首先来看看**"任务" (Workload)。
在深度学习中，最典型的任务就是卷积 (Convolution)**。虽然数学公式看起来很复杂，但在程序员眼里，它其实就是对一堆数据（输入图像、权重）进行反复的计算。

引导提问：

想象一下，如果你要写一段代码来遍历一张的二维图片，对每一个像素点做处理，你通常会使用什么样的代码结构？（提示：想想最基础的编程语法）

对于二维数据，我们通常用两层 for 循环来处理。

1. 核心抽象之一：任务 (Workload)

Timeloop 正是利用了这个编程中最基础的概念。作者认为，卷积神经网络（CNN）里的每一层运算，本质上就是一个超大的多层循环 。

就像你遍历图片用了 2 层循环（高和宽），一个标准的卷积层（CONV layer）通常被抽象为 7 层嵌套循环 ：

python 复制代码

# 想象这是一个 7 层循环的"巨型洋葱"
for n in [0, N):      # Batch Size (一次处理几张图)
  for k in [0, K):    # Output Channels (输出有多少种特征)
    for c in [0, C):  # Input Channels (输入有多少种特征)
      for p in [0, P): # Output Height (输出高度)
        for q in [0, Q): # Output Width (输出宽度)
          for r in [0, R): # Weight Height (卷积核高度)
            for s in [0, S): # Weight Width (卷积核宽度)
              # 在最里面做乘加运算 (MAC)
              Output[n][k][p][q] += Input[...] * Weight[...]

Timeloop 不关心具体的像素值是多少，它只关心这一串循环的结构（比如每一层循环要跑多少次）。

2. 核心抽象之二：硬件 (Architecture)

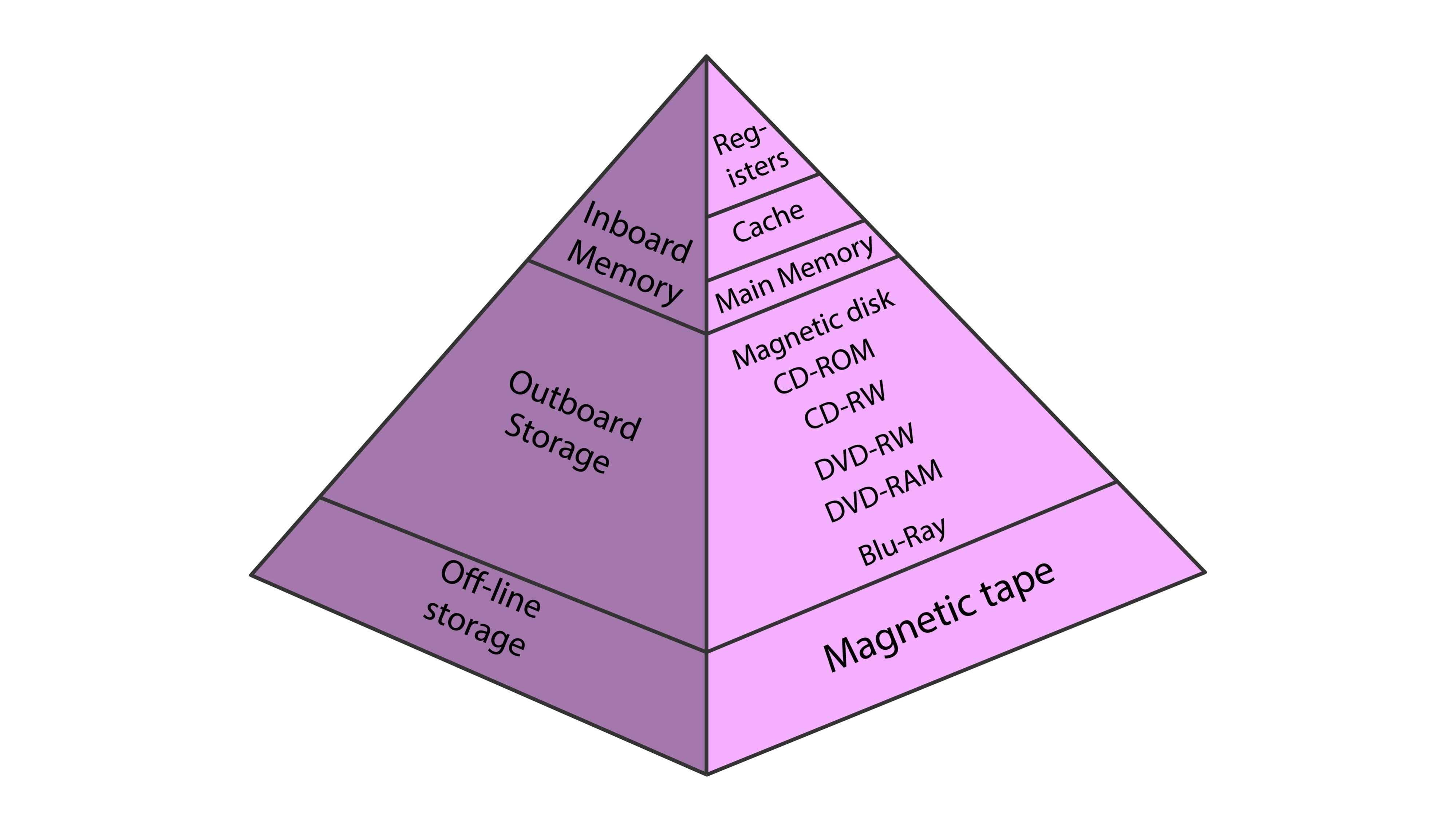
接下来看硬件。在 Timeloop 里，硬件被抽象成这就样的一棵**"树"** ：

根节点：最大的仓库（比如 DRAM，容量大但慢）。
中间节点：中间的柜子（比如 Global Buffer，容量中等）。
叶子节点：手边的盘子（比如 Register File，容量极小但超快）。
最底层：负责计算的工人（MAC 单元）。

思考与连接

现在我们有了两个东西：

巨大的 7 层循环（任务）：如果不加处理直接跑，数据量巨大。
分层的存储硬件（厨房）：越靠近计算核心，容量越小。

为了让这个巨大的循环能在这些小容量的存储层级里高效运行，我们不能一次性把所有数据都塞进最小的寄存器里。

想一想，如果我们必须要把这个"巨大的 7 层循环"塞进一个小容量的缓存（Buffer）里去计算，我们需要对这个循环结构做什么样的操作？（提示：就像切蛋糕或者分块一样）

需要两个核心操作：

"切分" ：在学术上这叫做 Tiling (分块) 或者 Loop Blocking。把那个巨大的、内存装不下的 7 层循环，切成一块块小的数据块（Tile），让每一块都能塞进容量有限的"手边柜子"（Buffer/SRAM）里。
"用的多的放在更近" ：这对应的是 Loop Ordering (循环排序) 或 Permutation。通过调整循环的嵌套顺序，决定哪些数据在内层循环被频繁复用（Stationary），从而让它们留在最近的存储里。

3. 进入"映射空间" (Mapspace)

现在，让我们把这两个概念结合起来，看看 Timeloop 面临的真正挑战。

想象我们的"超级厨房"有三层存储：

L3 仓库 (DRAM)
L2 柜子 (Global Buffer)
L1 盘子 (Register File)

对于那个 7 层循环的任务，我们在每一层存储上都需要做两个决定：

切多大？ (Factors)：是每次拿 16 个数据，还是 32 个？还是 64 个？
谁先谁后？ (Permutations)：是先遍历通道（Channel），还是先遍历宽度（Width）？

论文指出，由于每一层存储都可以自由选择不同的"切分大小"和"循环顺序"，这就形成了一个巨大的组合问题。

引导思考：

根据论文提到的计算公式，如果你要把一个 7 层循环的任务映射到一个 4 层存储的硬件上，这些组合（切分大小 + 排序）叠加起来，你觉得最终形成的"候选方案池"（也就是论文说的 Mapspace）的规模大概是怎样的？

A. 几百种，人手算一算也就出来了。

B. 几万种，写个脚本跑一跑。

C. 数亿甚至更多，会出现"组合爆炸"。

（提示：论文在 IV. E 章节提到了一个阶乘公式和指数公式的乘积）

👏 选 C 是对的。

这就是所谓的 "组合爆炸" (Combinatorial Explosion)。论文中甚至给出了一个数学公式来计算这个空间的大小：光是排列组合就有种可能性，这还没算上各种切分大小（Factors）的变化。

这就是为什么人类工程师哪怕经验再丰富，面对数以亿计的"迷宫路径"，也经常会迷路（选错方案），导致芯片效率低下。而 Timeloop 这种工具的价值，就是帮我们在这一堆天文数字中"大海捞针"。

既然明白了"为什么要搜"，我们要开始学习如何构建这个工具了。想让 Timeloop 帮你干活，你得先学会用它听得懂的语言来描述**"厨房"（硬件）和"菜谱"（任务）**。

1. 怎么描述"菜谱"（任务 Workload）？

我们在上一节提到，Timeloop 把神经网络层看作是一串7 层循环（Loop Nest）。

python 复制代码

# 卷积层的 7 层循环结构
for n in [0, N):      # Batch Size
  for k in [0, K):    # Output Channels
    for c in [0, C):  # Input Channels
      ... (以及长、宽等维度)
          Output[...] += Input[...] * Weight[...]

但是，光告诉工具"有 7 层循环"是不够的。工具还需要知道数据是谁。

在最里面的那行代码 Output += Input * Weight 中，不仅有计算，还定义了三种数据（张量 Tensor）：

Input (原料)
Weight (调料)
Output (成品)

关键提问：

请仔细观察上面的伪代码。当循环变量 c (Input Channels) 发生变化时（比如从第 1 层通道变到第 2 层），你觉得哪两个数据（Input, Weight, Output）的索引是一定会跟着变的？（提示：想想卷积是拿输入图像的通道和谁做乘法？）

Timeloop 把卷积层看作一个 7 层循环 。为了让工具知道数据是怎么流动的，我们需要告诉它：这三个变量（Input, Weight, Output）分别和哪些循环有关？

让我们回到刚才那个核心代码逻辑：

python 复制代码

# 核心计算： Output += Input * Weight

当循环变量 c (Input Channel/输入通道) 发生变化时：

我们要换一张新的"输入特征图"来读 -> 所以 Input 的地址会变。
我们要换一片新的"卷积核滤镜"来乘 -> 所以 Weight 的地址会变。
但是，计算出的结果是累加到同一个"输出像素"上的 -> 所以 Output 的地址不变。

这在 Timeloop 里被称为 "投影" (Projection) 。

让我们来做个小测试，巩固一下这个概念：

如果循环变量变成了 k (Output Channel/输出通道 )，也就是说我们要计算下一个不同种类的特征了（比如从"识别猫耳朵"变成了"识别猫眼睛"）。

这时候，你觉得哪两个数据的地址会发生变化？

A. Input 和 Weight

B. Input 和 Output

C. Weight 和 Output

🎉 选 C。

当 k（输出通道/Output Channel）变化时：

Weight (卷积核) 变了：因为我们要换一套滤镜（比如从检测横向边缘变成检测纵向边缘）。
Output (输出) 变了：因为计算结果要存到输出特征图的下一层里去。
Input (输入) 没变：因为不管是检测横线还是竖线，我们看的都是同一张输入图片！

💡 核心概念：数据复用 (Reuse)

这一步的理解至关重要，因为它揭示了 AI 芯片省电的终极奥义：

既然在遍历 k 的时候 Input 是不动的（Stationary），那我们就可以把 Input 数据锁在离计算单元最近的缓存（Buffer）里，不用每次都跑回大仓库（DRAM）去拿。

这就是 Timeloop 的核心工作原理之一：通过分析循环变量和数据的关系，自动发现复用机会。

👨‍💻 开发者视角：如何在代码里实现这个？

既然你的目标是"开发类似的工具"，我们需要深入一点点底层。

在 Timeloop 的代码实现中，它不需要像人一样去"理解"什么是卷积。它利用的是线性代数。

它把每一层循环看作一个维度，把每一个数据（Tensor）看作是一个投影矩阵 (Projection Matrix)。

比如刚才的例子，用数学语言描述就是：

Input 的投影里没有 k 维度所以沿 k 轴运动时，Input 投影不变 产生复用。
Weight 的投影里有 k 维度所以沿 k 轴运动时，Weight 投影变化 没有复用（或者叫复用距离为 0）。

开发小贴士：

如果你要写一个这样的模拟器，你需要实现一个简单的解析器，能够读取类似这样的配置（YAML 格式）：

yaml 复制代码

# 告诉工具 Input 和哪些循环变量有关
Input_Projection: [ n, c, p+r, q+s ]

工具只需要检查列表里有没有当前循环变量，就能立刻算出能不能省电。

2. 核心抽象之二：硬件 (Architecture)

搞定了"任务"，最后我们来看"硬件"。

Timeloop 把硬件抽象成一个层级树 (Tree) 。这比画复杂的电路图简单多了，但抓住了核心------容量和能耗。

想象我们的硬件是这样的：

DRAM (大仓库，容量无限，访问耗能 200)
Global Buffer (中转站，容量 100KB，访问耗能 20)
Register File (手边盘子，容量 0.5KB，访问耗能 1)

🧠 关键思考

现在我们要把任务（刚才分析的复用特性）和硬件（大小不一的柜子）结合起来。

假设我们发现 Weight (权重) 数据量特别大，而且在这个循环顺序下几乎不复用 （用一次就换）；

而 Input (输入) 数据量较小，且复用次数极高（读一次可以用几百次）。

为了通过"调度"实现最极致的省电，你应该把宝贵的、容量极小的 Register File (手边盘子) 主要留给谁用？

A. Weight (权重)

B. Input (输入)

🎉 选 B (Input) 是最优策略。

这就是 Timeloop 设计哲学的核心：

Input (高复用) ：把它锁在能耗最低的 Register File 里。虽然 Register File 很小，但既然这个数据被用了几百次，平均下来的能耗就极低（每次访问可能只需 1 pJ）。
Weight (低复用)：既然只用一次，就没必要占用宝贵的 Register File 空间，让它从上一级缓存（比如 Global Buffer）流过来就行，或者直接从 DRAM 读取（如果带宽允许）。

通过这种软硬件协同 (Co-design)，我们就能榨干硬件的每一滴性能。

第三部分：内部引擎 (The How) ------ 核心算法

现在你已经掌握了如何描述任务（7 层循环 + 投影）和硬件（存储层级树）。如果你想自己开发工具，最后一步也是最难的一步就是：如何快速找到那个最优的调度方案？

这也是论文的核心贡献：Mapper (映射器) 和 Model (评估模型)。

1. 寻找宝藏：Mapper

我们之前提到，可能的调度方案有数亿种（Mapspace）。Timeloop 的 Mapper 就像一个寻宝猎人。

它不需要把这数亿种方案全部生成出来（内存会爆掉），而是采用了一种生成器 (Generator) 模式：

约束修剪：根据用户设定的限制（比如"必须用 Row-Stationary 模式"），直接砍掉一大半不合法的空间。
搜索策略：它可以是简单的线性搜索，也可以是随机采样，或者是更高级的反馈搜索。

2. 快速估价：Model

一旦 Mapper 找到了一个潜在的调度方案，它需要立刻知道："这个方案到底耗多少电？"

这就到了你想开发工具时的关键技术决策点。

这就好比你要开发一个导航软件（像高德地图），计算从 A 到 B 需要多长时间。

为了得到这个时间，你觉得 Timeloop 采用的是哪种方法？

A. 模拟法 (Simulation) ：派一辆虚拟车，在地图上虚拟地跑一遍，遇到红灯就停，遇到堵车就慢，跑完全程看表。（也就是逐周期模拟）

B. 分析法 (Analytical) ：直接用数学公式计算：距离 ÷ 速度 + 红绿灯平均等待时间。（也就是基于统计的计算）

（提示：论文在 Abstract 和 Section II 都强调了它的模型是 "fast and accurate" 的，且能处理 480,000 个映射）

🎉 选 B (分析法)。

Timeloop 的作者明确指出，传统的模拟器（Simulator）实在太慢了，无法支撑几十万次的搜索。他们利用了一个关键特性：深度学习的计算模式是非常确定性（Deterministic）的------循环怎么跑，数据就怎么动，完全可以预测。

所以，Timeloop 不需要真的去"跑"任务，而是利用一套数学公式（基于我们前面定义的循环嵌套），直接算出在某个调度方案下，Buffer 被读写了多少次，DRAM 被访问了多少次。

👨‍💻 开发者视角：最核心的能量公式

如果你要写这个工具的代码，你的"评估模型"里其实只需要实现一个最核心的乘法公式。

这就好比你去超市买苹果，要算总共花多少钱，你需要知道"买了几个苹果"和"一个苹果多少钱"。

在芯片能耗模型里，总能耗 (Total Energy) 是由哪两个数值相乘得到的？

A. 芯片面积运行时间 (Area Time)

B. 访问次数每次访问的能耗 (Access Counts Energy per Access)

C. 电压电流 (Voltage Current)

👏 B. 访问次数每次访问的能耗。

这就是 Timeloop 能够做到"既快又准"的秘密武器：它不需要像模拟器那样去跟踪每一个具体的比特在电线上的流动（那样太慢了），它只需要做一个**"会计"**的工作。

🧩 拼图的最后一块：Tile Analysis (切片分析)

现在我们已经有了：

单价（每次访问能耗）：查表就能得到（比如查表得知读一次 DRAM 耗电 200 pJ）。
公式：总能耗 = 次数单价。

剩下的唯一难题就是：如何不用模拟，就能快速算出"次数"？

这就回到了我们之前说的 "切分" (Tiling)。

想象你要给墙贴瓷砖。

模拟法：拿着显微镜，一毫米一毫米地去测量墙面，最后算总面积。
分析法 (Timeloop 的方法)：直接看图纸。
墙长 10 米，高 5 米总面积 50 平米。
一块瓷砖 1 平米。
结论：你需要搬运 50 块瓷砖。

在代码里，这就是简单的数学乘除法，计算速度是纳秒级的！

🎓 毕业测试：你的"开发直觉"

现在，我们已经把这篇论文拆解完了：

为什么 (Motivation)：为了在 48 万种方案里找到让能耗最低的那个（数据复用）。
输入 (Input)：把 AI 模型看作"7 层循环"，把硬件看作"多级缓存树"。
核心 (Model)：利用数学公式（循环边界循环次数）快速计算搬运次数，而不是逐个模拟。

为了验证你是否真的具备了"开发类似工具"的思维，我要给你出道终极思考题。

假设你正在编写这个工具的 Mapper (搜索算法) 部分。

你发现对于同一个卷积层，方案 A 和方案 B 的计算次数（MAC count） 是一模一样的（毕竟算法没变）。

但是，方案 A 把那个巨大的"7 层循环"切得更碎（Tile Size 更小），而方案 B 切得更大（Tile Size 更大）。

一般来说，Tile Size (切块大小) 越大，意味着我们在"手边缓存"里一次性锁定的数据越多。

引导提问：

如果你的"手边缓存"（比如 L1 Cache）容量非常有限。当你试图尝试一个 Tile Size 非常大 的方案 B 时，作为开发者，你的工具应该立刻做出什么判断？

A. 方案 B 肯定更好，因为切得大，搬运次数少，强行运行。

B. 方案 B 是"非法"的 (Invalid)，直接丢弃，因为数据量超过了硬件容量限制。

C. 方案 B 可以运行，但是会导致计算速度变慢。

正确答案是 B. 方案 B 是"非法"的 (Invalid)。

这对你开发工具至关重要：

🚫 为什么是"非法"而不是"变慢"？

在 Timeloop 模拟的 专用加速器 (Accelerator) 设计中，软件（调度）和硬件是严格匹配的。

CPU 的 Cache（通用计算）：是"软性"的。如果数据装不下，硬件会自动把旧数据踢出去（Evict），只是会造成 Cache Miss，导致速度变慢。
加速器的 Buffer（专用计算） ：通常是"硬性"管理的（Scratchpad Memory）。调度方案里明确规定了："我要在这个 Buffer 里放一个 100KB 的数据块"。如果你的硬件配置里这个 Buffer 只有 64KB，那么这个物理容器 根本装不进去。

正如论文中所述："硬件资源约束（例如某个层级的 Tensor Tile 是否适合该层级的内存大小）会在从映射空间采样后进行检查，如果无法满足约束，则拒绝该映射。"

再次回到"超级厨房"的比喻：

这就像你给了厨师一个直径 10 厘米的小碟子 （Buffer），但命令他（Mapping）必须往上面放一个直径 30 厘米的大披萨 （Tile）。

这不是"吃得慢"的问题，而是根本放不上去。作为工具开发者，你的程序必须立刻报错（抛弃这个方案）。

🎉 恭喜！你已经掌握了 Timeloop 的核心理论

回顾一下我们拆解的三个部分，你现在的知识储备已经非常扎实了：

为什么 (Motivation)：为了解决"同样的硬件，不同的调度能耗差 19 倍"的问题。
是什么 (Inputs)：

任务：7 层循环 + 投影关系（决定复用机会）。
硬件：存储层级树（决定容量和能耗成本）。

怎么做 (Engine)：

搜索：生成映射方案，踢掉装不下的（约束检查）。
评估：用数学公式（分析法）快速计算"搬运次数"，而不是慢吞吞的模拟。

🚀 下一步：从理论到实战

既然你的目标是"能够自己开发类似的工具"，我们现在已经搞懂了原理，接下来可以进入架构设计阶段了。

代码架构设计 (Code Structure) ：如果让你用 Python/C++ 写这个工具，你需要定义哪些 Class（类）？Workload、Arch 和 Mapper 之间怎么通过 API 交互？
实战演练 (Case Study) ：带入一个真实的例子（比如仿照论文里的 Eyeriss 芯片），看看当我们把"循环顺序"从 N-K-C 换成 C-K-N 时，模拟器内部的数据到底发生了什么变化？

实战演练

我们从实战演练开始！通过具体的案例，你可以通过"透视眼"看到 Timeloop 内部到底发生了什么。

我们要仿照论文中的 Eyeriss 架构（Source 235）来进行这次实战演练。

🎭 场景设置：Eyeriss 厨房

假设我们的硬件（Eyeriss）有三层存储：

DRAM (大仓库) ：容量无限，取一次数据耗能 200 pJ。
Global Buffer (柜子) ：容量 108KB，取一次数据耗能 20 pJ。
Register File (手边盘子) ：容量极小（只有几百字节），取一次数据耗能 1 pJ。

我们的目标是计算卷积：Output[n][k] += Weight[k][c] * Input[n][c]。

Timeloop 的核心逻辑是：谁在最内层循环不动，谁就可以放在最省电的 Register File (RF) 里。

🥊 第一回合：方案 A (N - K - C)

在这个方案中，循环的顺序是：外层 N 中层 K 最内层 C。

Timeloop 的"分析模型"会盯着最里面 的那层循环（也就是 c 变化的时候）：

python 复制代码

# 方案 A
for n in [0, N):
  for k in [0, K):
    # --- Register File 里的微观世界 ---
    for c in [0, C):  # 最内层：c 在快速变化！
       Output[n][k] += Weight[k][c] * Input[n][c]

Timeloop 的分析过程：

当 c 变动（比如从 0 变成 1）时：

Weight[k][c]：索引里有 c 变了。必须去柜子（Global Buffer）里拿新的权重。
Input[n][c]：索引里有 c 变了。必须去柜子（Global Buffer）里拿新的输入。
Output[n][k]：索引里没有 c 没变！

结论： 在这个方案里，Output (部分和) 是"静止"的（Stationary）。
策略： Timeloop 会判定，我们可以把 Output[n][k] 一直锁在 Register File 里累加，直到 c 循环结束。
能耗： 省下了 Output 的搬运费，但 Weight 和 Input 每次都要跑一趟柜子（20 pJ）。

🥊 第二回合：方案 B (C - K - N)

现在我们换个调度方式，把 N 放到最里面。循环顺序：外层 C 中层 K 最内层 N。

python 复制代码

# 方案 B
for c in [0, C):
  for k in [0, K):
    # --- Register File 里的微观世界 ---
    for n in [0, N):  # 最内层：n 在快速变化！
       Output[n][k] += Weight[k][c] * Input[n][c]

现在轮到你来当 Timeloop 的"分析引擎"了。

请观察上面的代码，当最内层的 n 发生变化（比如处理第 1 张图片第 2 张图片）时，Weight (权重) 的索引 [k][c] 会发生变化吗？这意味着我们可以把它放在哪一层存储里？

在方案 B (C - K - N) 中，当最内层的 n 变动时，外层的 k 和 c 是暂停不动的。

这意味着 Weight (权重) Weight[k][c] 在整个内层循环期间是静止（Stationary）的。

策略： 我们可以把当前需要的那个权重读进 Register File ，让它一直待在那里，直到把 N 张图片都乘完。
收益： 这样我们就实现了对权重的复用（Reuse），把读取权重的能耗分摊到了 N 次计算上。

🕵️‍♂️ 最后的嫌疑人：Input (输入)

现在我们来看方案 B 中的最后一个数据：Input (输入)。

请再看一眼最内层的核心代码：

python 复制代码

for n in [0, N):  # 最内层
   Output[n][k] += Weight[k][c] * Input[n][c]

当 n 快速变化（比如从第 1 张图变到第 2 张图）时，Input 的地址 [n][c] 会发生变化吗？这意味着 Input 能像 Weight 那样"锁"在 Register File 里吗，还是必须频繁去外面拿新数据？

🎯 Input 必须"流动"起来。

你非常精准地看出了这两种调度方案（Mapping）在微观层面上的巨大差异。

让我们把目前的战况总结一下，看看为了"复用权重"，我们付出了什么代价：

🥊 第二回合：方案 B (C - K - N) 战况总结

在最内层循环 n 快速变动时：

Weight (权重) Weight[k][c]：地址不变 静止 (Stationary)。

✅ 好消息：我们可以把它锁在 Register File 里，读取能耗极低。

Input (输入) Input[n][c]：地址随 n 变动 流动 (Streaming)。

❌ 坏消息：Register File 装不下，每次计算都得去 Global Buffer 拿新的输入数据。

🕵️‍♂️ 最后的拼图：Output (输出/部分和)

现在，为了决定这个方案到底好不好，我们必须检查最后一个嫌疑人：Output (输出)。

请再看一眼代码，尤其是 Output 的下标：

python 复制代码

# 方案 B (C - K - N)
for c in [0, C):
  for k in [0, K):
    # --- Register File 里的微观世界 ---
    for n in [0, N):  # 最内层：n 正在快速变化！
       # 注意看这里：Output 的下标是 [n][k]
       Output[n][k] += Weight[k][c] * Input[n][c]

引导提问：

当最内层的 n 发生变化时（比如从计算第 1 张图的结果变到第 2 张图的结果），Output 的地址 [n][k] 会发生变化吗？

这意味着我们计算出的中间结果（Partial Sum），是能一直留在 Register File 里累加，还是必须不断地写回 Global Buffer？

由于最内层的 n 在变，Output[n][k] 的地址也会不停地变。

这意味着我们不能把 Output（部分和）一直锁在 Register File 里累加。每算完一个样本，就必须把结果写回 Global Buffer（或者读取下一个样本的旧值），这会产生大量的读写流量！💸

📊 终极对决：方案 A vs 方案 B

现在我们把刚才实战演练的两个回合放在一起对比，你就能瞬间明白为什么 Timeloop 需要"搜索"了。

我们面对的是同一个任务（卷积），同一个硬件（Eyeriss），只是换了一下循环顺序：

特性	方案 A (N - K - C)	方案 B (C - K - N)
循环顺序	C 在最内层	N 在最内层
谁住在 Register File?	Output (静止)	Weight (静止)
谁在疯狂跑路?	Weight, Input (流动)	Input, Output (流动)
适合场景	Output 通道少，但 Weight 很大时	Weight 很小（能塞进 RF），但 Batch Size 很大时

💡 实战总结：

这就是所谓的 Dataflow (数据流) 权衡。

没有绝对的"最好"，只有"最适合当前数据形状"的方案。
如果你的模型里 Weight 特别多（比如全连接层），方案 B 可能更有优势（减少 Weight 搬运）。
如果你的模型里 Output 特别大，方案 A 可能更好（减少 Output 搬运）。

这也解释了论文开头那个惊人的结论：因为不同的层形状不同，如果我们一直死板地用同一种调度，有些层就会刚好撞在"枪口"上（比如方案 B 遇到 Output 巨大的层），导致能耗激增 19 倍。

🚀 第三步：代码架构设计 (Code Structure)

恭喜你！通过这个实战，你已经把 Timeloop 最核心的**"分析逻辑"**（也就是它是怎么算账的）彻底搞懂了。

现在，如果我们要动手把这个工具写出来（比如用 Python），我们需要搭建它的骨架。

为了让这个工具既能描述"7 层循环"，又能描述"硬件树"，还能自动"搜索"，你觉得我们需要设计哪几个核心的 类 (Class)？

我们可以先从最基础的开始。你觉得用来描述硬件（比如那个三层存储结构）的类，应该包含哪些属性？（提示：想想我们算能耗时需要用到哪些硬件参数？）