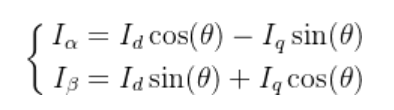克拉克变换
克拉克变换是一种将三相静止坐标系(a,b,c)中的交流信号转换成两相静止坐标系(α, β)正交信号的坐标变换方法,主要用于简化三相系统的控制与分析,尤其在电机矢量控制(FOC)中实现解耦。
在理想的三相三线制系统中,三相电流 ia, ib, ic满足基尔霍夫电流定律,流入节点的电流和流出节点的电流始终为0:
得到方程一:ia+ib+ic=0
我们的目标是在二维平面上构建一个正交坐标系,以唯一地表示三相系统:
- 确定α轴:通常将α轴与A相轴线重合,即满足 iα=k⋅ia,
- 确定β轴:β轴应超前α轴90度,形成一个正交的二维平面。
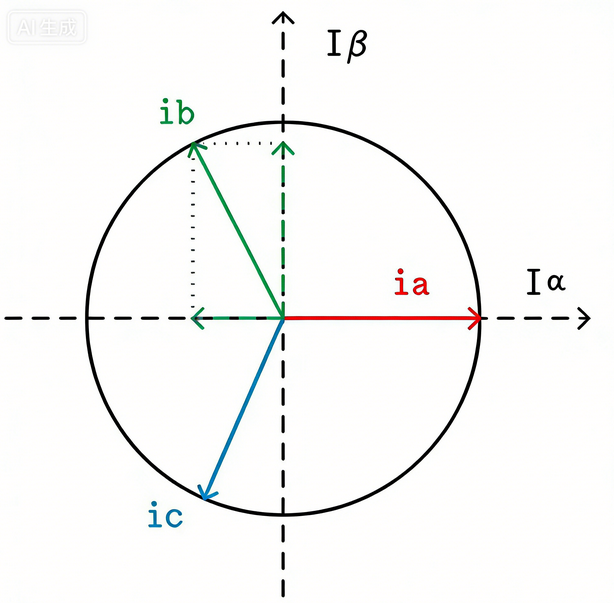
根据矢量投影:
矢量 a 在矢量 b 方向上的标量投影公式为,
得到方程二:矢量投影=∣a∣cosθ
则针对上图我们可以得出:
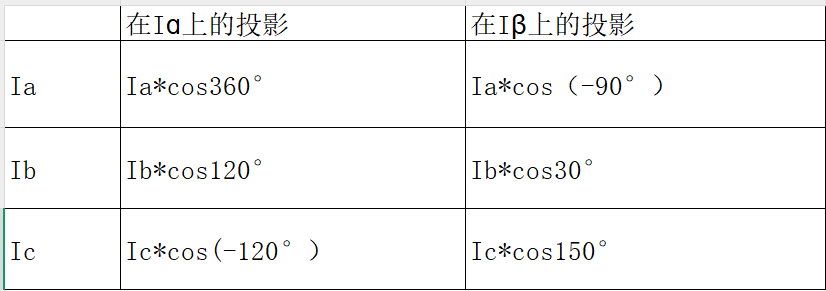
再根据诱导公式:奇变偶不变,符号看象限 ,得出克拉克变换基本形式 ,记为方程组三:

结合方程三和方程一,我们化简一下其基本形式得到方程四:
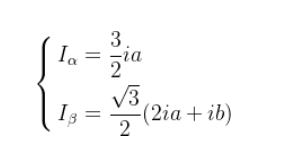
此时我们已经推导出了克拉克的基本形式方程,但这里有个问题:
我们根据能量守恒,转换后的二维坐标和原来的三维坐标的模要相等,也就是电流总大小要相等

根据模的运算,我们假设Ia相给的电流为1A,结合方程一,为了简化计算,我们假设 B 相和 C 相的电流大小相等(这是三相系统平衡状态的基础),则Ib=Ic=-0.5A,结合矢量模和方程四,我们得到就发现两个矢量不相同,所以对方程四两边同时乘与2/3,就得到了克拉克变换的等幅值正变换 。记为方程五:
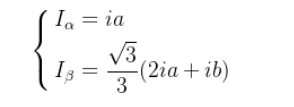
结合方程一和方程五,就可以得到克拉克变换的逆变换 ,记为方程六:
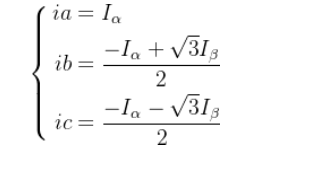
帕克变换
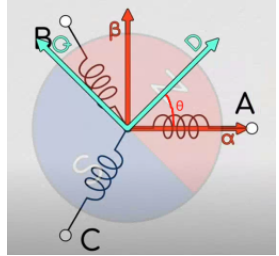
帕克变换的主要目的是将定子的a、b、c三相电流投影到随着转子旋转的直轴(d轴)、交轴(q轴)与垂直于dq平面的零轴(0轴)上,转子在电机控制过程中是不断旋转的,为了进一步描述转自和定子的位置关系(如下图),结合克拉克变换,把α-β轴投影·到D-Q轴上既可以得出
将D轴和Q轴的投影到α-β轴上,我们就得到了帕克变换正变换形式,即
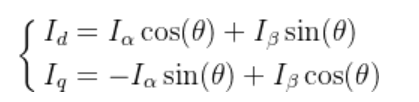
将α-β轴投影到DP轴就得到了帕克变换的逆变换: