强化学习入门：核心概念与数学基础详解

褪色的博客2025-12-26 14:38

强化学习入门第一课：核心概念与数学基础详解

本博客讲的类容比较基础，方便零基础同学入门学习。

更专业的讲解，可以参考王树森老师或者赵世钰老师的讲解。

一、什么是强化学习（Reinforcement Learning, RL）：

如果你不能直接告诉 AI "该怎么做"， 只能靠"奖励"和"惩罚"来引导它------ 它能自己学会打游戏、开小车、下围棋吗？

答案是：能！

这就是强化学习 的神奇之处。

它不像监督学习那样需要"标准答案"，也不像无监督学习只找模式，而是模拟生物试错学习的过程：

例如：

小孩摸火 → 烫 → 哭 → 下次不摸

狗狗坐下 → 得零食 → 开心 → 下次更愿坐下

强化学习的智能体（Agent）就是这样，在与环境不断互动中，自己一点点总结出规律，从而明确"什么环境中做什么动作"能获取最高的任务收益。

二、基础铺垫：概率基础（理解随机，概率计算，以及什么是期望）

在强化学习中的一切几乎都是随机的，所以我们先复习概率学中的两个核心概念------概率和期望。

▶ 离散 vs 连续：世界有两种"不确定性"

类型 名称 特点 例子
离散型 概率质量函数（PMF） 只能取有限/可数值 投骰子、抽卡片、选动作
连续型 概率密度函数（PDF） 可取无限多个实数值 机器人手臂角度、车速、温度
✅ PMF 例子：袋子里有 10 个球
  • 红球 2 个 → 抽中红球概率 = 0.2
  • 绿球 5 个 → 概率 = 0.5
  • 蓝球 3 个 → 概率 = 0.3

记作：
p ( 红 ) = 0.2 , p ( 绿 ) = 0.5 , p ( 蓝 ) = 0.3 p(\text{红}) = 0.2,\quad p(\text{绿}) = 0.5,\quad p(\text{蓝}) = 0.3 p(红)=0.2,p(绿)=0.5,p(蓝)=0.3

所有可能结果的概率之和 = 1。

PDF 例子：身高分布（高斯分布）
  • 平均身高 μ = 170 cm，标准差 σ = 10 cm
  • PDF 曲线中间高、两边低：
    p ( x ) = 1 2 π σ exp ⁡ ( − ( x − μ ) 2 2 σ 2 ) p(x) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) p(x)=2π σ1exp(−2σ2(x−μ)2)
    注意：PDF 的纵坐标不是概率，而是"相对可能性"；必须对一段区间积分，才是真实概率。

核心工具：期望（Expectation）

一句话定义期望：

期望 = 所有可能结果 × 其发生可能性 的加权平均值

它不是某次具体结果，而是在大量重复实验下，你"最该预期"得到的长期平均水平。

它就像一个"上帝视角"的预言家------不告诉你下一次抽到什么，但能准确预言：如果你玩 10000 次，总分大概会落在哪附近。这就类似于一个围棋高手，即使棋局还没下完，但是仅凭当前残局，就能分析你当前的胜算。

为什么需要「期望」？期望可以帮助我们消除随机变量的影响

我们关心的不再是"某一次结果"，而是长期平均表现。

很多人混淆「样本均值」和「期望」。我们用一个例子厘清：

情境：从袋子中抽球（共 10 个）
  • 红球 2 个 → 得 10 元
  • 绿球 5 个 → 得 5 元
  • 蓝球 3 个 → 扣 20 元
【期望】（理论值，固定不变）：

这是由规则本身决定的"先天属性" ，只要袋子组成不变，期望就固定：
E [ R ] = 0.2 ⏟ 红概率 × 10 + 0.5 ⏟ 绿概率 × 5 + 0.3 ⏟ 蓝概率 × ( − 20 ) = − 1.5 元 \mathbb{E}[R] = \underbrace{0.2}{\text{红概率}} \times 10 + \underbrace{0.5}{\text{绿概率}} \times 5 + \underbrace{0.3}_{\text{蓝概率}} \times (-20) = -1.5\ \text{元} E[R]=红概率 0.2×10+绿概率 0.5×5+蓝概率 0.3×(−20)=−1.5 元
无论你玩不玩，这个数都是 -1.5。它是「游戏是否公平」的黄金标准。

【样本均值】（观测值，随次数波动）：

这是你实际玩若干局后的算术平均：

  • 玩 1 局：抽到红球 → 平均 = +10 元
  • 玩 3 局：红、绿、蓝 → 平均 = ( 10 + 5 − 20 ) / 3 = − 1.67 (10 + 5 - 20)/3 = -1.67 (10+5−20)/3=−1.67 元
  • 玩 1000 局：可能 ≈ -1.48 元
  • 玩 1,000,000 局：≈ -1.5002 元（越来越接近期望！）

当实验次数趋于无穷时，样本均值以概率 1 收敛于期望值。

也就是说------

🔹 期望是「理论极限」

🔹 样本均值是它的「近似估计」

🔹 RL 算法，本质上就是用有限样本去逼近期望价值

1️⃣离散型随机变量（取值可列）

设 X X X 是离散随机变量，取值集合为 X = { x 1 , x 2 , x 3 , ...   } \mathcal{X} = \{x_1, x_2, x_3, \dots\} X={x1,x2,x3,...}，

其概率质量函数（PMF） 为 p ( x ) = P ( X = x ) p(x) = \mathbb{P}(X = x) p(x)=P(X=x)。

则对任意函数 f ( X ) f(X) f(X)，其期望定义为：
E [ f ( X ) ] = ∑ x ∈ X p ( x ) ⋅ f ( x ) \boxed{ \mathbb{E}[f(X)] = \sum_{x \in \mathcal{X}} p(x) \cdot f(x) } E[f(X)]=x∈X∑p(x)⋅f(x)

  • 求和遍历所有可能取值
  • 每项是「结果大小 × 发生概率」
  • 若 f ( X ) = X f(X) = X f(X)=X，则 E [ X ] \mathbb{E}[X] E[X] 就是均值（mean）

再看抽球例子（令 X X X = 颜色， R = f ( X ) R = f(X) R=f(X) = 奖金）：

x x x（颜色） p ( x ) p(x) p(x) f ( x ) f(x) f(x)（奖金） p ( x ) ⋅ f ( x ) p(x) \cdot f(x) p(x)⋅f(x)
红 0.2 +10 +2.0
绿 0.5 +5 +2.5
蓝 0.3 -20 -6.0
总和 1.0 --- -1.5 ✅

期望奖金 = -1.5 元。

2️⃣ 连续型随机变量（取值充满区间）

设 X X X 是连续随机变量，在区间 X ⊆ R \mathcal{X} \subseteq \mathbb{R} X⊆R 上取值，

其概率密度函数（PDF） 为 p ( x ) p(x) p(x)，满足：
p ( x ) ≥ 0 , ∫ X p ( x )   d x = 1 p(x) \geq 0,\quad \int_{\mathcal{X}} p(x)\,dx = 1 p(x)≥0,∫Xp(x)dx=1

则对任意函数 f ( X ) f(X) f(X)，其期望定义为：
E [ f ( X ) ] = ∫ X p ( x ) ⋅ f ( x )   d x \boxed{ \mathbb{E}[f(X)] = \int_{\mathcal{X}} p(x) \cdot f(x)\,dx } E[f(X)]=∫Xp(x)⋅f(x)dx

  • p ( x ) p(x) p(x) 本身不是概率！ 它是"概率的密度"；
  • 真实概率需对区间积分： P ( a ≤ X ≤ b ) = ∫ a b p ( x )   d x \mathbb{P}(a \leq X \leq b) = \int_a^b p(x)\,dx P(a≤X≤b)=∫abp(x)dx
实例：机器人手臂角度偏差

假设控制器让机械臂指向 90°，但由于噪声，实际角度 X X X 服从高斯分布：

  • 均值 μ = 90 ∘ \mu = 90^\circ μ=90∘，标准差 σ = 5 ∘ \sigma = 5^\circ σ=5∘
  • PDF： p ( x ) = 1 2 π ⋅ 5 exp ⁡ ( − ( x − 90 ) 2 2 ⋅ 5 2 ) p(x) = \dfrac{1}{\sqrt{2\pi}\cdot 5} \exp\left(-\dfrac{(x - 90)^2}{2 \cdot 5^2}\right) p(x)=2π ⋅51exp(−2⋅52(x−90)2)

我们关心角度偏差的平方 （控制误差）： f ( X ) = ( X − 90 ) 2 f(X) = (X - 90)^2 f(X)=(X−90)2

则期望误差为：
E [ ( X − 90 ) 2 ] = ∫ − ∞ ∞ ( x − 90 ) 2 ⋅ p ( x )   d x = σ 2 = 25 \mathbb{E}[(X - 90)^2] = \int_{-\infty}^{\infty} (x - 90)^2 \cdot p(x)\, dx = \sigma^2 = 25 E[(X−90)2]=∫−∞∞(x−90)2⋅p(x)dx=σ2=25

这就是方差（Variance） ！它本身就是一种期望： V a r ( X ) = E [ ( X − μ ) 2 ] \mathrm{Var}(X) = \mathbb{E}[(X - \mu)^2] Var(X)=E[(X−μ)2]

三、强化学习的基本元素（非常重要，一切的基础，务必背下来）

我们用一个经典例子贯穿始终：
超级马里奥

1️⃣ 智能体（Agent）

决策者，根据当前信息选择动作。

在这个例子中就是马里奥本人，它负责观察、决策、行动。

2️⃣ 环境（Environment）

动态系统，接收动作、给出新状态与奖励。

在这个例子中就是整个游戏世界：砖块、敌人、金币、关卡规则等，它接收马里奥的动作，更新世界，并给出反馈。

二者交互过程如下：

python 复制代码 
s₀ → Agent → a₀ → Environment → (r₀, s₁) → Agent → a₁ → ...

3️⃣ 状态（State s s s）

描述环境在某一时刻的完整可观测信息（如游戏画面、机器人关节角度）。

在这个例子中就是马里奥当前看到的画面信息 （如位置、敌人距离、剩余时间）

注意：状态不一定是完整地图！现实中智能体往往只能看到局部（称为「部分可观测」）。

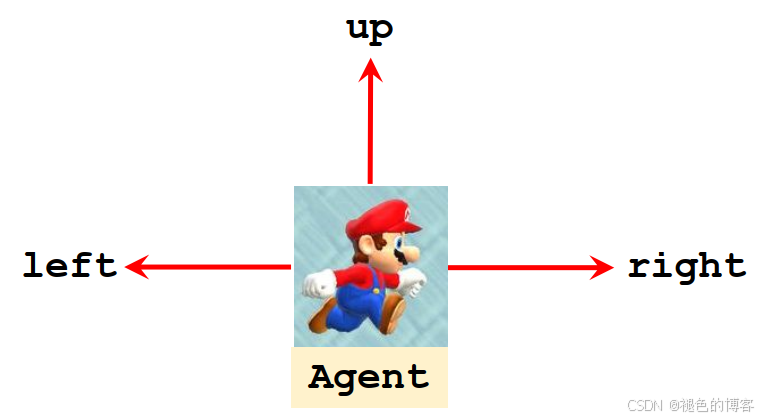
4️⃣ 动作（Action a a a）

智能体在状态 s s s 下可执行的操作集合。

例如：马里奥能做的操作：{左, 右, 跳}

记作动作空间 A = { left , right , jump } \mathcal{A} = \{\text{left}, \text{right}, \text{jump}\} A={left,right,jump}

5️⃣策略（Policy）

决策规则：映射状态到动作的分布。

定义为在状态 s s s 下，选择每个动作的概率是多少？

π ( a ∣ s ) = P ( A = a ∣ S = s ) \pi(a \mid s) = \mathbb{P}(A = a \mid S = s) π(a∣s)=P(A=a∣S=s)

在这个例子中马里奥在状态 s s s下，可能的策略是：

动作 a a a π ( a ∣ s ) \pi(a \mid s) π(a∣s)
上（吃金币） 0.7
左（后退，为吃金币做准备） 0.2
右 （前进，会碰到敌人） 0.1

注意这是一个随机策略（Stochastic Policy）。

为什么需要随机性？

  • 避免卡死在局部最优（比如只顾眼前金币，不向前探索）
  • 允许"探索"新动作------就像人偶尔会尝试新路线

6️⃣奖励（Reward r r r）

→ 环境给的即时反馈，数值越大学习效果越好

例如：

事件 奖励 r r r
吃到金币 + 1 +1 +1
踩死敌人 + 10 +10 +10
赢得游戏 + 1000 +1000 +1000
碰到敌人 − 1000 -1000 −1000（游戏结束）
啥也没干 0 0 0

奖励是 RL 的唯一监督信号！ 智能体不知道"目标是什么"，只认"分数高低"。

四、回报（Return）与折扣（Discounting）

智能体的目标不是最大化单步奖励，而是长期累积收益。单步奖励（如 +1）意义不大，关键是：整局游戏的总分！

定义从时间 t t t 开始的回报（Return） ：
U t = R t + R t + 1 + R t + 2 + ⋯ + R T U_t = R_t + R_{t+1} + R_{t+2} + \cdots + R_T Ut=Rt+Rt+1+Rt+2+⋯+RT

其中 T T T 是游戏结束时刻（如马里奥通关 or 死亡）。

但有个问题：未来的奖励，和现在的奖励等价吗？

现在我给你两个选项

💰 选 A：现在拿 80 元

💰 选 B：1 年后拿 100 元

我相信大部分人选 A， 因为"现在的一块钱比未来的一块钱更值钱"

为了衡量现在奖励与未来奖励之间的这种折扣关系，于是引入折扣因子（Discount Factor） γ ∈ [ 0 , 1 ] \gamma \in [0, 1] γ∈[0,1]，定义折扣回报 ：
U t = R t + γ R t + 1 + γ 2 R t + 2 + ⋯ + γ T − t R T U_t = R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots + \gamma^{T-t} R_T Ut=Rt+γRt+1+γ2Rt+2+⋯+γT−tRT

γ \gamma γ 值 行为风格 适用场景
0.0 极度短视 马上要关机的机器人
0.9 平衡眼前与长远 大多数游戏、控制任务
0.99 非常有耐心 长期规划（如自动驾驶）

实际中 γ = 0.9 ∼ 0.99 \gamma = 0.9 \sim 0.99 γ=0.9∼0.99 很常见------差 1 ∼ 10 % 1\sim10\% 1∼10% 的折扣，可能让智能体从"苟活"进化到"夺冠"！

五、环境如何响应？------状态转移（State Transition）

马里奥执行动作后，环境会给出新状态 和奖励 。

这个过程由状态转移函数描述：

p ( s ′ ∣ s , a ) = P ( S ′ = s ′ ∣ S = s , A = a ) p(s' \mid s, a) = \mathbb{P}(S' = s' \mid S = s, A = a) p(s′∣s,a)=P(S′=s′∣S=s,A=a)

环境不确定性：

马里奥在选择向上跳之后，环境会随之更新，但是环境的更新存在不确定性，例如图中敌人的运动轨迹：

  • 80% 向左移动 →（ s 1 ′ s_1' s1′）
  • 20% 向右移动 →（ s 2 ′ s_2' s2′）

即：
p ( s 1 ′ ∣ s , 右 ) = 0.8 , p ( s 2 ′ ∣ s , 右 ) = 0.2 p(s_1' \mid s, \text{右}) = 0.8,\quad p(s_2' \mid s, \text{右}) = 0.2 p(s1′∣s,右)=0.8,p(s2′∣s,右)=0.2

注意：这种随机性来自环境，不是智能体控制的。

两个随机性来源（极易混淆！务必厘清）

强化学习中的不确定性来自两方面：

来源 谁控制？ 数学表示 类比
动作随机性 智能体（策略 π \pi π） A ∼ π ( ⋅ ∣ s ) A \sim \pi(\cdot \mid s) A∼π(⋅∣s) 你决定"80% 概率加油门"
状态转移随机性 环境（随机性 p p p） S ′ ∼ p ( ⋅ ∣ s , a ) S' \sim p(\cdot \mid s, a) S′∼p(⋅∣s,a) 路面结冰导致车打滑

这两种随机性的叠加，导致后续所有奖励都变成随机变量！

六、如何评估一个决策的好坏？------价值函数登场！

上面分析了由于强化学习中的两个随机性 动作随机性 和状态转移随机性 ，导致回报 U t U_t Ut 是随机的：

  • U t = R t + γ R t + 1 + γ 2 R t + 2 + ⋯ + γ T − t R T U_t = R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots + \gamma^{T-t} R_T Ut=Rt+γRt+1+γ2Rt+2+⋯+γT−tRT
  • 而 R k R_k Rk 依赖于 ( S k , A k ) (S_k, A_k) (Sk,Ak)
  • S k + 1 ∼ p ( ⋅ ∣ S k , A k ) S_{k+1} \sim p(\cdot \mid S_k, A_k) Sk+1∼p(⋅∣Sk,Ak) → 环境随机
  • A k ∼ π ( ⋅ ∣ S k ) A_k \sim \pi(\cdot \mid S_k) Ak∼π(⋅∣Sk) → 策略随机

所以：即使固定了当前状态 S t = s S_t = s St=s 和动作 A t = a A_t = a At=a ，后续的
( S t + 1 , A t + 1 , R t + 1 ,    S t + 2 , A t + 2 , R t + 2 ,    ...   ) (S_{t+1}, A_{t+1}, R_{t+1},\; S_{t+2}, A_{t+2}, R_{t+2},\; \dots) (St+1,At+1,Rt+1,St+2,At+2,Rt+2,...)

仍然充满随机性！

这就导致：同一个 ( s , a ) (s, a) (s,a)，重复玩 10 次，可能得到 10 个不同的 u t u_t ut（实现值） 。

但如果我们关心「跳这个动作到底靠不靠谱 」，就不能看某一次运气，而要看长期平均表现，这时期望就派上了用场。

动作价值函数 Q π ( s , a ) Q^\pi(s, a) Qπ(s,a)

"在状态 s s s 下，先选动作 a a a ，之后都按策略 π \pi π 走------预期总分是多少？ "

用于衡量在当前状态 s s s ，动作 a a a的好坏。

Q π ( s , a ) = E [   U t   ∣   S t = s ,   A t = a   ] Q^\pi(s, a) = \mathbb{E}\big[\, U_t \,\big|\, S_t = s,\, A_t = a \,\big] Qπ(s,a)=E[Ut St=s,At=a]

我们通过对回报 U t U_{t} Ut 求期望，从而消除未来路径的随机性，保留一个"只依赖策略 π \pi π 和环境模型 p p p"的确定数值。

具体消除哪些随机变量？
变量 是否被条件化（固定）？ 是否仍随机？ 是否被期望"平均掉"？
S t S_t St ✅ 固定为 s s s 否 ---
A t A_t At ✅ 固定为 a a a 否 ---
S t + 1 , A t + 1 , R t + 1 S_{t+1}, A_{t+1}, R_{t+1} St+1,At+1,Rt+1 ❌ ✅ ✔️ 被 E [ ⋅ ] \mathbb{E}[\cdot] E[⋅] 平均
S t + 2 , A t + 2 , R t + 2 S_{t+2}, A_{t+2}, R_{t+2} St+2,At+2,Rt+2 ❌ ✅ ✔️
⋮ \vdots ⋮

换句话说：

  • 我们人为设定："此时此刻，马里奥就在金币前（ S t = s S_t = s St=s），并且它决定跳（ A t = a A_t = a At=a）"
  • 但从 t + 1 t+1 t+1 步开始，一切按规则随机演化（环境按 p p p 转移，马里奥按 π \pi π 选动作）
  • Q π ( s , a ) Q^\pi(s, a) Qπ(s,a) 就是在上述前提下，所有可能未来轨迹的回报加权平均

它衡量的是：动作 a a a 在状态 s s s 下的"长期平均潜力"，与单次运气无关。

状态价值函数 V π ( s ) V^\pi(s) Vπ(s)

对动作价值函数 Q π ( s , a ) Q^\pi(s, a) Qπ(s,a)求动作 A t A_t At 的期望，进一步消除"当前动作 A t A_t At 的随机性"，得到仅关于状态 s s s 和策略 π \pi π 的价值。

用于衡量当前状态对于结果的好坏。

V π ( s ) = E A ∼ π ( ⋅ ∣ s ) [   Q π ( s , A )   ] = ∑ a π ( a ∣ s ) ⋅ Q π ( s , a ) V^\pi(s) = \mathbb{E}{A \sim \pi(\cdot \mid s)} \big[\, Q^\pi(s, A) \,\big] = \sum{a} \pi(a \mid s) \cdot Q^\pi(s, a) Vπ(s)=EA∼π(⋅∣s)[Qπ(s,A)]=a∑π(a∣s)⋅Qπ(s,a)

消除哪些变量？
变量 是否被平均掉？
未来轨迹 ( S t + 1 , A t + 1 , ...   ) (S_{t+1}, A_{t+1}, \dots) (St+1,At+1,...) 已由 Q π Q^\pi Qπ 的期望消掉
当前动作 A t A_t At 由 V π V^\pi Vπ 的期望 再次消掉

最终 V π ( s ) V^\pi(s) Vπ(s) 的含义是：

"马里奥当前在状态 s s s，之后完全交给策略 π \pi π 自动决策------长期平均能得多少分？"

它不再关心"这一步具体选什么"，只评估"按这套策略走，这个局面整体是好是坏"。

两层期望，两层抽象

函数 表达式 消除的随机性 用途
回报 U t U_t Ut R t + γ R t + 1 + ⋯ R_t + \gamma R_{t+1} + \cdots Rt+γRt+1+⋯ 无 单次实验的得分（随机、不可靠）
Q π ( s , a ) Q^\pi(s, a) Qπ(s,a) E [ U t ∣ S t = s , A t = a ] \mathbb{E}[U_t \mid S_t=s, A_t=a] E[Ut∣St=s,At=a] 未来路径 ( S t + 1 , A t + 1 , ...   ) (S_{t+1}, A_{t+1}, \dots) (St+1,At+1,...) 评估某个具体动作的长期价值（微观决策）
V π ( s ) V^\pi(s) Vπ(s) E A ∼ π [ Q π ( s , A ) ] \mathbb{E}_{A \sim \pi}[Q^\pi(s, A)] EA∼π[Qπ(s,A)] 当前动作 A t A_t At + 未来路径 评估某个状态 + 策略组合的整体好坏（宏观局势）

类比：炒股决策

场景 U t U_t Ut Q π ( s , a ) Q^\pi(s, a) Qπ(s,a) V π ( s ) V^\pi(s) Vπ(s)
你看到某支股票跌到 10 元（状态 s s s） 买 100 股后，3 个月亏了 5000（单次结果） "如果此刻买入"，历史回测平均年化收益 +8% "按我的交易系统（策略 π \pi π）"，当股价=10 元时，平均胜率 62%、期望盈亏比 1.5

专业投资者不看单次盈亏（ U t U_t Ut），而是依赖回测期望（ Q π Q^\pi Qπ）与系统评估（ V π V^\pi Vπ）做决策。

七、实战第一步：用 OpenAI Gym 动手试试！

OpenAI Gym 是 RL 的"标准实验台"，提供大量预设环境。

🎯 推荐入门任务：CartPole（推杆平衡）

  • 目标：移动小车，让杆子不倒
  • 动作：2 种 ------ 小车左移 / 右移
  • 状态：4 维向量（位置、速度、角度、角速度）
  • 奖励：每坚持 1 步，+1 分（满分 500）

一段超简代码体验交互：

python 复制代码 
import gym

env = gym.make("CartPole-v1")
state = env.reset()     # 初始状态
total_reward = 0

for t in range(500):
    action = env.action_space.sample()      # 随机选动作（瞎玩）
    next_state, reward, done, _ = env.step(action)  # 执行
    total_reward += reward
    env.render()          # 弹窗看动画（可选）
    if done:
        break

print(f"坚持了 {t+1} 步，总得分：{total_reward}")

运行几次你会发现：随机策略只能撑 10~30 步 。

而人类/RL 算法可达 500 步 ------ 这就是"学习"的力量！

相关推荐
遥感学习森2 小时前
滑雪场分布API及滑雪预报服务API
大数据·人工智能·天气api
code bean2 小时前
【AI】RAG智能问答的三层优化策略
大数据·人工智能·rag
代码洲学长2 小时前
RNN模型01
人工智能·python·rnn·自然语言处理·gru·lstm
t198751282 小时前
经典的KSVD图像字典学习
人工智能·学习·计算机视觉
树獭非懒2 小时前
AI大模型小白手册 | API调用的魔法指南
人工智能·llm·aigc
跨境小渊2 小时前
从“冷启动”到“热转化”——DeepBI赋能listing优化：实战案例揭示投放新突破
人工智能
泰迪智能科技2 小时前
分享|陕西高校大数据人工智能实验室建设内容+建设成效
大数据·人工智能
TOWE technology2 小时前
智联电力基石：从运维视角看数据中心PDU的演进与未来
大数据·人工智能·数据中心·pdu·智能pdu·定制电源管理·idc数据中心
热门推荐
01GitHub 镜像站点02从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击033D 圣诞树网页代码04UV安装并设置国内源05Linux下V2Ray安装配置指南06在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）07Gemini3 生成的基于手势控制3D粒子圣诞树08解决 WSL Ubuntu 中 /etc/resolv.conf 自动重置问题09开源分享 | 超浪漫 3D 圣诞树立体动画（附零基础使用教程）10GLM-4.7 vs MiniMax-M2.1：代码工程理解