6关系数据理论

第六章关系数据理论

一、为什么需要关系数据理论？

一个设计不良的关系模式（如将所有信息塞进一张大表）会存在严重问题：

数据冗余：相同的信息被存储多次。
更新异常：更新一条信息时，需要修改多处，容易造成数据不一致。
插入异常：无法插入某些信息，除非它依赖的另一个（可能还未发生的）信息也存在。
删除异常：删除某条信息时，导致了另一条有用信息的丢失。

核心问题 ：这些异常的根源在于关系模式中存在"不合适的数据依赖"。
解决方法 ：通过模式分解，消除这些不合适的依赖。
基本工具：函数依赖 (FD) 及其公理系统。

二、数据依赖的公理系统

1. 逻辑蕴含

定义6.11：对于关系模式 R<U, F>（U是属性全集，F是函数依赖集），如果某个函数依赖 X→YX \to YX→Y 对于 R 的任何一个 满足 FFF 的关系实例 rrr 都成立，那么称 FFF 逻辑蕴含 X→YX \to YX→Y。
- X→YX\rightarrow YX→Y的含义为对rrr中任意两元组ttt和sss，若t[X]=s[X]t[X]=s[X]t[X]=s[X]，则t[Y]=s[Y]t[Y]=s[Y]t[Y]=s[Y]。
F+F^+F+ (F的闭包) ：被 FFF 逻辑蕴含的所有函数依赖的集合。

2. Armstrong 公理系统

这是一套有效且完备的推理规则，用于从已知的 FFF 推导出所有 F+F^+F+ 中的依赖。

基本规则 (3条)：

A1. 自反律 ：若 Y⊆X⊆UY \subseteq X \subseteq UY⊆X⊆U，则 X→YX \to YX→Y 被 FFF 蕴含。
- 通俗讲：一组属性总能决定它自己的子集。（例如：(学号, 姓名) →\to→ 学号）
A2. 增广律 ：若 X→YX \to YX→Y 被 FFF 蕴含，且 Z⊆UZ \subseteq UZ⊆U，则 XZ→YZXZ \to YZXZ→YZ 被 FFF 蕴含。
- 通俗讲：已有的依赖，两边加上相同的属性，依赖仍然成立。
A3. 传递律 ：若 X→YX \to YX→Y 且 Y→ZY \to ZY→Z 被 FFF 蕴含，则 X→ZX \to ZX→Z 被 FFF 蕴含。
- 这是产生"传递依赖"的根源，也是 3NF 要消除的对象。

导出规则 (3条)（由基本规则推导，非常常用）：

合并规则 ：由 X→YX \to YX→Y 且 X→ZX \to ZX→Z，有 X→YZX \to YZX→YZ。
分解规则 ：由 X→YX \to YX→Y 且 Z⊆YZ \subseteq YZ⊆Y，有 X→ZX \to ZX→Z。
- 引理 6.1 ：X→A1A2...AkX \to A_1 A_2 ... A_kX→A1A2...Ak 成立的充要条件是 X→AiX \to A_iX→Ai (对所有 i=1,...,ki=1, ..., ki=1,...,k) 均成立。
伪传递规则 ：由 X→YX \to YX→Y 且 WY→ZWY \to ZWY→Z，有 XW→ZXW \to ZXW→Z。

引理6.1：X→A1A2...AkX\rightarrow A_1A_2\dots A_kX→A1A2...Ak成立的充分必要条件是X→AiX\rightarrow A_iX→Ai成立(i=1,2,...,k)(i=1,2,\dots,k)(i=1,2,...,k)。

3. 属性集的闭包 (XF+X_F^+XF+)

定义6.13：设 X⊆UX \subseteq UX⊆U， XF+X_F^+XF+ (属性集 X 关于 F 的闭包) 被定义为：
XF+={A∣X→A 能由 F 根据 Armstrong 公理导出 } X_F^+ = \{ A \mid X \to A \text{ 能由 F 根据 Armstrong 公理导出 } \} XF+={A∣X→A 能由 F 根据 Armstrong 公理导出 }

通俗讲： XF+X_F^+XF+ 就是从 X 出发，利用 F 中的依赖，能够决定的所有属性的集合。

引理6.2：设FFF为属性集UUU上的一组函数依赖，X,Y⊆UX,Y\subseteq UX,Y⊆U，X→YX\rightarrow YX→Y能由FFF根据Armstrong公理导出的充分必要条件是Y⊆XF+Y\subseteq X_F^+Y⊆XF+。

引理 6.2的重要用途：

判断 X→YX \to YX→Y 是否成立 ：计算 XF+X_F^+XF+，检查是否 Y⊆XF+Y \subseteq X_F^+Y⊆XF+。
求候选码 ：如果 XF+=UX_F^+ = UXF+=U (UUU是全集)，则 XXX 是关系 RRR 的一个超码。如果此时 XXX 又是最小的（其任何真子集的闭包都不等于 UUU），则 XXX 是候选码。

算法 6.1：求属性集**XXX **关于FFF 的闭包 XF+X_F^+XF+，这是一个迭代算法：

令 X(0)=XX^{(0)} = XX(0)=X。
X(i+1)=X(i)∪BX^{(i+1)} = X^{(i)} \cup BX(i+1)=X(i)∪B，其中 B={A∣存在 V→W∈F 且 V⊆X(i) 且 A∈W}B = \{ A \mid \text{存在 } V \to W \in F \text{ 且 } V \subseteq X^{(i)} \text{ 且 } A \in W \}B={A∣存在 V→W∈F 且 V⊆X(i) 且 A∈W}。
重复步骤 2，直到 X(i+1)=X(i)X^{(i+1)} = X^{(i)}X(i+1)=X(i) (无法再添加新属性)。
此时 XF+=X(i)X_F^+ = X^{(i)}XF+=X(i)。

【例题 1】 已知 R<U,F>R<U, F>R<U,F>，U=A,B,C,D,EU={A,B,C,D,E}U=A,B,C,D,E；F=AB→C,B→D,C→E,EC→B,AC→BF={AB\to C, B\to D, C\to E, EC\to B, AC\to B}F=AB→C,B→D,C→E,EC→B,AC→B。求 (AB)F+(AB)_F^+(AB)F+。

解：

设 X(0)=ABX^{(0)} = ABX(0)=AB。
第1轮迭代 ：
- 检查 FFF：
- AB→CAB\to CAB→C：AB⊆X(0)AB \subseteq X^{(0)}AB⊆X(0)，将 C 加入。X(1)=ABCX^{(1)} = ABCX(1)=ABC。
- B→DB\to DB→D：B⊆X(1)B \subseteq X^{(1)}B⊆X(1)，将 D 加入。X(1)=ABCDX^{(1)} = ABCDX(1)=ABCD。
- C→EC\to EC→E：C⊆X(1)C \subseteq X^{(1)}C⊆X(1)，将 E 加入。X(1)=ABCDEX^{(1)} = ABCDEX(1)=ABCDE。
第2轮迭代 ：
- X(1)=ABCDEX^{(1)} = ABCDEX(1)=ABCDE 已经是全集 UUU。
- （继续检查：EC→\to→B，EC⊆ABCDEEC \subseteq ABCDEEC⊆ABCDE，B 已在集中；AC→\to→B，AC⊆ABCDEAC \subseteq ABCDEAC⊆ABCDE，B 已在集中）
- X(2)=ABCDEX^{(2)} = ABCDEX(2)=ABCDE。
X(2)=X(1)X^{(2)} = X^{(1)}X(2)=X(1)，算法终止。 (AB)F+=ABCDE(AB)_F^+ = ABCDE(AB)F+=ABCDE。
- 推论：AB 是该关系模式的候选码（因为它能决定所有属性）。

4.Armstrong公理系统的有效性与完备性

有效性 ：由FFF出发，根据Armstrong公理推导出来的每一个函数依赖一定在F+F^+F+中；
完备性 ：F+F^+F+中的每一个函数依赖，必定可以由FFF出发根据Armstrong公理推导出来。

定理6.2 Armstrong公理系统是有效的 、完备的。

5.函数依赖集等价

定义6.14 ：如果G+=F+G^+=F^+G+=F+，就说函数依赖集FFF覆盖GGG（FFF是GGG的覆盖，或GGG是FFF的覆盖），或FFF与GGG等价。

两个函数依赖集等价是指它们的闭包等价

6. 最小依赖集 ( FmF_mFm)

定义6.15：如果函数依赖集FmF_mFm满足下列条件，则称FmF_mFm为一个最小依赖集。

FmF_mFm 中任一函数依赖的右部仅含一个属性。
FmF_mFm 中不存在 这样的函数依赖 X→AX \to AX→A，使得 FmF_mFm 与 Fm−{X→A}F_m - \{X \to A\}Fm−{X→A} 等价。（即：即FFF中的函数依赖均不能由FFF中其他函数依赖导出）。
FmF_mFm 中不存在 这样的函数依赖 X→AX \to AX→A，XXX 有真子集 Z⊂XZ \subset XZ⊂X 使得 Fm−{X→A}∪{Z→A}F_m - \{X \to A\} \cup \{Z \to A\}Fm−{X→A}∪{Z→A} 与 FmF_mFm 等价。（即：没有冗余的左部属性）。

求最小依赖集的三步算法：

将FFF中的所有函数依赖的右边化为单一属性；
去掉FFF中的所有函数依赖左边的冗余属性；
去掉FFF中所有冗余的函数依赖。

【例题 2】 求 F={A→BD,AB→C,C→D}F = \{A\to BD, AB\to C, C\to D\}F={A→BD,AB→C,C→D} 的最小依赖集 FmF_mFm。

解： 第 1 步：右部分解 (使用分解规则) F1={A→B,A→D,AB→C,C→D}F_1 = \{ A \to B, A \to D, AB \to C, C \to D \}F1={A→B,A→D,AB→C,C→D}

第 2 步：消除左部冗余属性 (逐一检查)

只需检查 AB→CAB \to CAB→C。
(1) 检查 A 是否冗余：即 B→CB \to CB→C 是否能被 F1F_1F1 推出？
- 计算 B+B^+B+ (在 F1F_1F1 下)：B(0)=BB^{(0)} = BB(0)=B。B(1)=BB^{(1)} = BB(1)=B。BF1+=BB_{F_1}^+ = BBF1+=B。
- C∉BF1+C \notin B_{F_1}^+C∈/BF1+，所以 B→CB \to CB→C 不成立。A 不冗余。
(2) 检查 B 是否冗余：即 A→CA \to CA→C 是否能被 F1F_1F1 推出？
- 计算 A+A^+A+ (在 F1F_1F1 下)：A(0)=AA^{(0)} = AA(0)=A。
- A→B ⟹ A(1)=ABA \to B \implies A^{(1)} = ABA→B⟹A(1)=AB。
- A→D ⟹ A(1)=ABDA \to D \implies A^{(1)} = ABDA→D⟹A(1)=ABD。
- AB→C ⟹ A(1)=ABCDAB \to C \implies A^{(1)} = ABCDAB→C⟹A(1)=ABCD。
- AF1+=ABCDA_{F_1}^+ = ABCDAF1+=ABCD。
- C∈AF1+C \in A_{F_1}^+C∈AF1+，所以 A→CA \to CA→C 成立。B 是冗余的。
去掉 B，得到： F2={A→B,A→D,A→C,C→D}F_2 = \{ A \to B, A \to D, A \to C, C \to D \}F2={A→B,A→D,A→C,C→D}

第 3 步：消除冗余的依赖 (逐一检查)

(1) 检查 A→BA \to BA→B：在 G=F2−{A→B}={A→D,A→C,C→D}G = F_2 - \{A \to B\} = \{A \to D, A \to C, C \to D\}G=F2−{A→B}={A→D,A→C,C→D} 中求 AG+A_G^+AG+。
- AG+={A,D,C}A_G^+ = \{A, D, C\}AG+={A,D,C}。B∉AG+B \notin A_G^+B∈/AG+。不冗余。
(2) 检查 A→DA \to DA→D：在 G=F2−{A→D}={A→B,A→C,C→D}G = F_2 - \{A \to D\} = \{A \to B, A \to C, C \to D\}G=F2−{A→D}={A→B,A→C,C→D} 中求 AG+A_G^+AG+。
- AG+={A,B,C}A_G^+ = \{A, B, C\}AG+={A,B,C} (来自 A→B,A→CA \to B, A \to CA→B,A→C)
- ... 再用 C→D ⟹ {A,B,C,D}C \to D \implies \{A, B, C, D\}C→D⟹{A,B,C,D}。
- AG+={A,B,C,D}A_G^+ = \{A, B, C, D\}AG+={A,B,C,D}。D∈AG+D \in A_G^+D∈AG+。A→DA \to DA→D 是冗余的 (因为 A→C,C→D ⟹ A→DA \to C, C \to D \implies A \to DA→C,C→D⟹A→D)。
去掉 A→DA \to DA→D，得到 F3={A→B,A→C,C→D}F_3 = \{ A \to B, A \to C, C \to D \}F3={A→B,A→C,C→D}。
(3) 检查 A→CA \to CA→C：在 G={A→B,C→D}G = \{A \to B, C \to D\}G={A→B,C→D} 中求 AG+A_G^+AG+。AG+={A,B}A_G^+ = \{A, B\}AG+={A,B}。C∉AG+C \notin A_G^+C∈/AG+。不冗余。
(4) 检查 C→DC \to DC→D：在 G={A→B,A→C}G = \{A \to B, A \to C\}G={A→B,A→C} 中求 CG+C_G^+CG+。CG+={C}C_G^+ = \{C\}CG+={C}。D∉CG+D \notin C_G^+D∈/CG+。不冗余。

最终结果 ：最小依赖集 Fm={A→B,A→C,C→D}F_m = \{ A \to B, A \to C, C \to D \}Fm={A→B,A→C,C→D}。

注意：最小依赖集不唯一，取决于检查的顺序。

7. 候选码的计算 (重点)

属性分类：

L 类 (Left) ：仅出现在 F 函数依赖左部的属性。
R 类 (Right) ：仅出现在 F 函数依赖右部的属性。
N 类 (Neither) ：在 F 左右两部均未出现的属性。
LR 类 (Both) ：在 F 左右两部均出现的属性。

求解定理 (重要结论)：

L 类和 N 类属性 必须包含在 R 的任意候选码中。（因为它们不能被任何其他属性推导出来）。
R 类属性 一定不包含在 R 的任何候选码中。
LR 类属性 可能是候选码的组成部分。

求解步骤：

找出 L, R, N, LR 四类属性。
令 X=L∪NX = L \cup NX=L∪N。XXX 是候选码的"核心"。
计算 XF+X_F^+XF+。
Case 1 ：若 XF+=UX_F^+ = UXF+=U (全集)，则 XXX 是 R 的唯一候选码。
Case 2 ：若 XF+≠UX_F^+ \neq UXF+=U，则需要从 LR 类属性中选取若干属性 YYY，与 XXX 组合，使得 (X∪Y)F+=U(X \cup Y)_F^+ = U(X∪Y)F+=U。从 YYY 最小（1个属性）开始测试，所有满足条件的最小组合 (X∪Y)(X \cup Y)(X∪Y) 都是候选码。

【例题 3】 设 R(U,F)R(U, F)R(U,F)，U=(A,B,C,D,E)U=(A,B,C,D,E)U=(A,B,C,D,E), F=A→B,BC→E,ED→ABF={A\to B, BC \to E, ED \to AB}F=A→B,BC→E,ED→AB。求 R 的所有候选码。

解：

分类：
- 左部属性：{A, B, C, E, D}
- 右部属性：{B, E, A, B}
- L 类 (仅左)：{C, D}
- R 类 (仅右)：∅
- N 类 (均无)：∅
- LR 类 (两边)：{A, B, E}
求核心 ：X=L∪N={C,D}X = L \cup N = \{C, D\}X=L∪N={C,D}。
计算核心闭包 ：
- (CD)F+={C,D}(CD)_F^+ = \{C, D\}(CD)F+={C,D}。(F 中没有 C→...C\to...C→..., D→...D\to...D→... 或 CD→...CD\to...CD→...)
Case 2 ：(CD)F+≠U(CD)_F^+ \neq U(CD)F+=U。需要从 LR={A, B, E} 中添加属性。
组合测试 ：
- (1) 加 A ：求 (CDA)F+(CDA)_F^+(CDA)F+
  - X(0)={C,D,A}X^{(0)} = \{C, D, A\}X(0)={C,D,A}
  - 用 A→B ⟹ {A,B,C,D}A \to B \implies \{A, B, C, D\}A→B⟹{A,B,C,D}
  - 用 BC→E ⟹ {A,B,C,D,E}BC \to E \implies \{A, B, C, D, E\}BC→E⟹{A,B,C,D,E} = U
  - ACD 是一个候选码。
- (2) 加 B ：求 (CDB)F+(CDB)_F^+(CDB)F+
  - X(0)={C,D,B}X^{(0)} = \{C, D, B\}X(0)={C,D,B}
  - 用 BC→E ⟹ {B,C,D,E}BC \to E \implies \{B, C, D, E\}BC→E⟹{B,C,D,E}
  - 用 ED→AB ⟹ {A,B,C,D,E}ED \to AB \implies \{A, B, C, D, E\}ED→AB⟹{A,B,C,D,E} = U
  - BCD 是一个候选码。
- (3) 加 E ：求 (CDE)F+(CDE)_F^+(CDE)F+
  - X(0)={C,D,E}X^{(0)} = \{C, D, E\}X(0)={C,D,E}
  - 用 ED→AB ⟹ {A,B,C,D,E}ED \to AB \implies \{A, B, C, D, E\}ED→AB⟹{A,B,C,D,E} = U
  - ECD 是一个候选码。

最终结果 ：R 的候选码为 ACD, BCD, ECD。

三、关系范式判断指南

判断一个关系模式 RRR 属于第几范式，需要遵循一个严格的、逐级递增的检查流程 (1NF →\to→ 2NF →\to→ 3NF →\to→ BCNF →\to→ 4NF) 。一个模式属于 nnn 范式，必须首先满足 n−1n-1n−1 范式。

在开始判断之前，必须先完成以下工作：

找出 UUU：确定关系模式 RRR 的所有属性 集合 UUU。
找出 FFF：确定该模式上成立的所有函数依赖 集合 FFF。
找出 KKK：基于 FFF，求出 RRR 的所有候选码。
分类属性 ：
- 主属性 ：包含在任何一个候选码中的属性。
- 非主属性：不包含在任何候选码中的属性。

范式判断流程 (逐级检查)

第 1 步：判断是否为 1NF (第一范式)

定义 ：关系模式 RRR 的所有属性都是不可分的原子数据项。
如何判断 ：
- 检查表中是否**有"表中有表"**的情况
- 检查是否有属性是"组合项"（如"基本工资, 岗位津贴, ..."合并为"工资"）。
- 在当今的关系数据库设计中，1NF 是最基本的要求，我们通常默认满足。
结论：如果属性都是原子的，则满足 1NF。否则，不属于关系范式。

第 2 步：判断是否为 2NF (第二范式)

前提：必须首先满足 1NF。
定义：在 1NF 基础上，每一个非主属性 都完全函数依赖 于 RRR 的候选码。
如何判断（找反例） ：
- 检查是否存在"部分函数依赖"。
- 注意：这一步仅在"候选码是复合属性（由多个属性组成）"时才有意义。如果候选码是单个属性，则该模式（若为1NF）自动满足 2NF。
- 检查每一个非主属性 AAA：
  - 它是否依赖于候选码的某一个真子集（部分）？
  - 如果存在任何一个非主属性 AAA 依赖于码的一部分 ，则不满足 2NF。
  - 如果所有非主属性都必须依赖整个候选码（不能只依赖一部分），则满足 2NF。
例子
- 模式：SLC(Sno, Sdept, Sloc, Cno, Grade)
- 预备工作 ：
  - UUU: {Sno, Sdept, Sloc, Cno, Grade}
  - FFF: {(Sno, Cno) →\to→ Grade, Sno →\to→ Sdept, Sdept →\to→ Sloc, Sno →\to→ Sloc}
  - 候选码 KKK：(Sno, Cno)
  - 主属性 ：{Sno, Cno}
  - 非主属性 ：{Sdept, Sloc, Grade}
- 判断 2NF ：
  - 检查非主属性 Grade：它依赖于 (Sno, Cno)。这是对码的完全依赖。 (OK)
  - 检查非主属性 Sdept：它依赖于 Sno。Sno 是候选码 (Sno, Cno) 的一个真子集（一部分）。
  - 结论：发现了部分函数依赖 Sno -> Sdept。因此，SLC 不满足 2NF，它只停留在 1NF。

第 3 步：判断是否为 3NF (第三范式)

前提：必须首先满足 2NF。
定义) ：在 2NF 基础上，消除非主属性 对候选码的传递函数依赖。
如何判断（找反例） ：
- 检查是否存在"传递函数依赖"。
- 是否存在这样一个链条：K→A→BK \to A \to BK→A→B，其中：
  1. KKK 是候选码。
  2. AAA 是一个非主属性。
  3. BBB 是一个非主属性。
  4. A→KA \to KA→K 不成立 (即 AAA 不反过来决定 KKK)。
- 如果存在这样的链条，则不满足 3NF。
- 如果不存在 ，则满足 3NF。
例子
- 模式：SL(Sno, Sdept, Sloc)
- 预备工作 ：
  - FFF: {Sno $\to$ Sdept, Sdept $\to$ Sloc}
  - 候选码 KKK：(Sno)
  - 主属性 ：{Sno}
  - 非主属性 ：{Sdept, Sloc}
- 判断 2NF ：
  - 候选码 (Sno) 是单个属性，不是复合属性。
  - 结论：自动满足 2NF。
- 判断 3NF ：
  - 检查是否存在 K→A→BK \to A \to BK→A→B 的链条 (K=Sno, A/B为非主属性)：
  - 我们发现：Sno (K) →\to→ Sdept (非主属性) →\to→ Sloc (非主属性)。
  - 结论：发现了传递函数依赖 。因此，SL 不满足 3NF，它只停留在 2NF。

第 4 步：判断是否为 BCNF (Boyce-Codd 范式)

前提：必须首先满足 3NF。
定义：在 3NF 基础上，要求所有函数依赖（包括主属性之间的依赖）的决定因素 都必须包含候选码 （即决定因素必须是超码）。
如何判断（找反例）：
- 找出 FFF 中的所有函数依赖 X→YX \to YX→Y (包括 FFF 自身和 FFF 蕴含的)。
- 对每一个 非平凡的 X→YX \to YX→Y：
  - 检查 XXX 是不是一个超码？（判断方法：计算 XXX 的闭包 X+X^+X+，看 X+X^+X+ 是否等于 UUU*？*）
- 如果存在任何一个 X→YX \to YX→Y (Y不属于X)，它的 XXX 不是超码 ，则不满足 BCNF。
- 如果所有 X→YX \to YX→Y 的 XXX 都是超码 ，则满足 BCNF。
例子
- 模式：STJ(S, T, J) (学生S, 教师T, 课程J)
- 预备工作：
  - FFF: {(S, J) →\to→ T, (S, T) →\to→ J, T $\to$ J}
  - 候选码 KKK：(S, J) 和 (S, T)
  - 主属性 ：{S, T, J} (所有属性都是主属性)
  - 非主属性 ：∅\emptyset∅
- 判断 2NF / 3NF：
  - 因为没有非主属性，所以该模式不可能存在"部分依赖"或"传递依赖"。
  - 结论：自动满足 3NF。
- 判断 BCNF：
  - 检查 FFF 中的所有 FDs：
  - 1. (S, J) -> T：决定因素 (S, J) 是候选码，是超码。 (OK)
  - 1. (S, T) -> J：决定因素 (S, T) 是候选码，是超码。 (OK)
  - 1. T -> J：决定因素是 T。
    - T 是超码吗？我们计算 TTT 的闭包 T+T^+T+：
    - T+T^+T+ = {T, J}。(因为 T →\to→ J)
    - T+T^+T+ 不等于 {S, T, J}。
    - 所以 T 不是超码。
  - 结论：发现了决定因素 T 不是超码的函数依赖 T -> J。因此，STJ 不满足 BCNF，它只停留在 3NF。

第 5 步：判断是否为 4NF (第四范式)

前提：必须首先满足 BCNF。
定义：在 BCNF 基础上，消除非平凡且非函数依赖的多值依赖。
如何判断（找反例） ：
- 找出模式中的所有多值依赖 (MVD) X→→YX \to\to YX→→Y。
- 如果存在一个非平凡的 MVD X→→YX \to\to YX→→Y (Y不属于X, XY也不等于U)，并且 XXX 不是超码 ，则不满足 4NF。
- 如果所有非平凡 MVD 的决定因素 XXX 都是超码 ，则满足 4NF。
例子
- 模式：Teaching(C, T, B) (课程C, 教师T, 参考书B)
- 预备工作 ：
  - 语义：一门课©有一组教师(T)，有一组参考书(B)，且T和B互相独立（PPT Slide 63图示）。
  - FFF: ∅\emptyset∅ (没有函数依赖)
  - MVD ：{C →\to→ T, C →\to→ B}
  - 候选码 KKK：(C, T, B) (全码)
- 判断 BCNF ：
  - 因为没有非平凡的 函数依赖 ，所以自动满足 BCNF。
- 判断 4NF ：
  - 检查 MVD：C -> T
  - 决定因素是 C。
  - C 是超码吗？C+C^+C+ = {C}，不是超码。
  - 结论：发现了决定因素 C 不是超码的多值依赖 C ->> T。因此，Teaching 不满足 4NF，它只停留在 BCNF。

总结：范式判断速查表

范式	满足条件 (必须已满足上一级范式)	检查"反例"：是否存在...
1NF	属性都是原子的。	"表中有表"或"组合属性"。
2NF	非主属性完全依赖于码。	部分依赖 (非主属性依赖于码的一部分)。
3NF	非主属性不传递依赖于码。	传递依赖 (非主属性 BBB 依赖于另一个非主属性 AAA)。
BCNF	每个函数依赖的决定因素都是超码。	X→YX \to YX→Y，但 XXX 不是超码。
4NF	每个多值依赖的决定因素都是超码。	X→→YX \to\to YX→→Y，但 XXX 不是超码。

四、模式的分解

定义6.16 ：将关系模式 R<U,F>R<U, F>R<U,F> 分解为 ρ={R1<U1,F1>,R2<U2,F2>,...}\rho = \{ R_1<U_1, F_1>, R_2<U_2, F_2>, ... \}ρ={R1<U1,F1>,R2<U2,F2>,...}，其中 U=∪UiU = \cup U_iU=∪Ui，并且没有Ui⊆UJ,1≤i,j≤nU_i \subseteq U_J , 1\le i , j\le nUi⊆UJ,1≤i,j≤n。

1. 分解的三个准则

准则 1：无损连接性

ρ={R1<U1,F1>,...,Rn<Un,Fn>}ρ=\{R_1<U_1, F_1>, ..., R_n<U_n, F_n>\}ρ={R1<U1,F1>,...,Rn<Un,Fn>}是 R<U,F>R<U, F>R<U,F>的一个分解，若对R<U,F>R<U, F>R<U,F>的任何一个关系 rrr 均有 r=r在ρ中各关系模式上投影的自然连接成立r = r在ρ中各关系模式上投影的自然连接成立r=r在ρ中各关系模式上投影的自然连接成立，则称分解ρρρ具有无损连接性 。简称ρ为无损分解。
这是必须满足的最低标准。如果分解不具有无损连接性，会导致信息丢失或产生虚假元组。只有具有无损连接性的分解才能够保证不丢失信息。无损连接性不一定能解决插入异常、删除异常、修改复杂、数据冗余等问题。

准则 2：保持函数依赖

ρ={R1<U1,F1>,...,Rn<Un,Fn>}ρ=\{R_1<U_1, F_1>, ..., R_n<U_n, F_n>\}ρ={R1<U1,F1>,...,Rn<Un,Fn>} 是 R<U,F>R<U, F>R<U,F> 的一个分解，若F所逻辑蕴含的函数依赖一定也为分解后所有的关系模式中的函数依赖 FiF_iFi 所逻辑蕴含，即F+=(F1∪F2∪...∪Fn)+F^ + = ( F_1 ∪ F_2 ∪ ... ∪ F_n )^ +F+=(F1∪F2∪...∪Fn)+，则称关系模式RRR的这个分解是保持函数依赖的。
如果 FDs 不被保持，那么在数据更新时，就无法在单个子关系上检查数据一致性，而必须连接多个表才能检查，代价高昂。

准则3 ：分解既要具有无损连接性 ，又要保持函数依赖。

【S-L 模式分解示例】

初始状态分析

关系模式: S−L(Sno,Sdept,Sloc)S-L(Sno, Sdept, Sloc)S−L(Sno,Sdept,Sloc)
函数依赖:
- Sno→SdeptSno \rightarrow SdeptSno→Sdept (学号决定系别)
- Sdept→SlocSdept \rightarrow SlocSdept→Sloc (系别决定宿舍楼)
问题: 存在 Sno→Sdept→SlocSno \rightarrow Sdept \rightarrow SlocSno→Sdept→Sloc 的传递依赖。这意味着数据有冗余，且存在插入/删除/更新异常。

第一种分解情况

分解方案 ：将表拆成了三份 ------ SN(Sno)SN(Sno)SN(Sno), SD(Sdept)SD(Sdept)SD(Sdept), SO(Sloc)SO(Sloc)SO(Sloc)。

这是最糟糕的分解，把属性完全孤立了，分解后：
- 表SN里只有一堆学号。
- 表SD里只有一堆系名。
- 表SO里只有一堆宿舍号。
后果：丢失了所有联系，不知道哪个学号属于哪个系，也不知道哪个系在哪个楼。这些数据变成了毫无意义的碎片。
结论： 既不具有无损连接性，也未保持函数依赖。 (不可取)

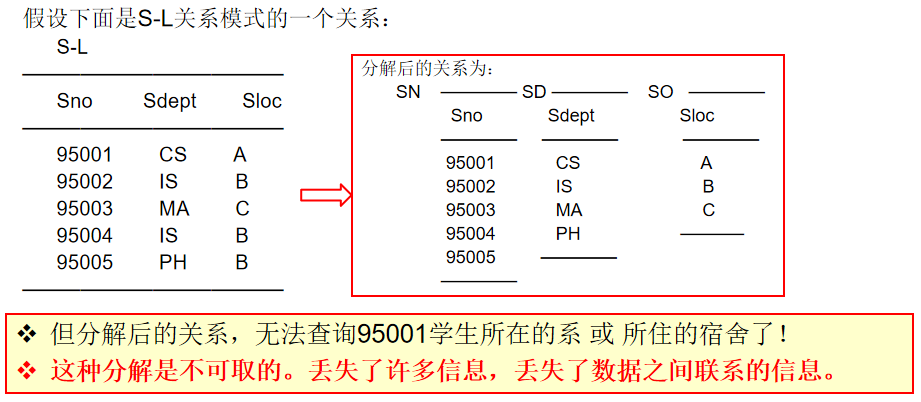
第二种分解情况

分解方案 ：NL(Sno,Sloc)NL(Sno, Sloc)NL(Sno,Sloc) 和 DL(Sdept,Sloc)DL(Sdept, Sloc)DL(Sdept,Sloc)。这里选择用 SlocSlocSloc（宿舍楼）作为两个表的公共属性（连接点）。

例如 IS系和 PH系都在宿舍楼 B。
- 原本95002是IS系的（在B楼），95005是PH系的（在B楼）。
- 当通过"B楼"这个公共点把两个表连回去时，数据库会困惑：95002到底是在IS系还是PH系？因为它只知道95002在B楼，而B楼里既有IS也有PH。
会导致数据库产生了虚假元组 ，原来的表只有5行数据，连接回去后变成了8行,多出来的3行是无中生有的错误数据（例如把IS系的学生错误地连到了PH系，只因为他们住同一栋楼）。
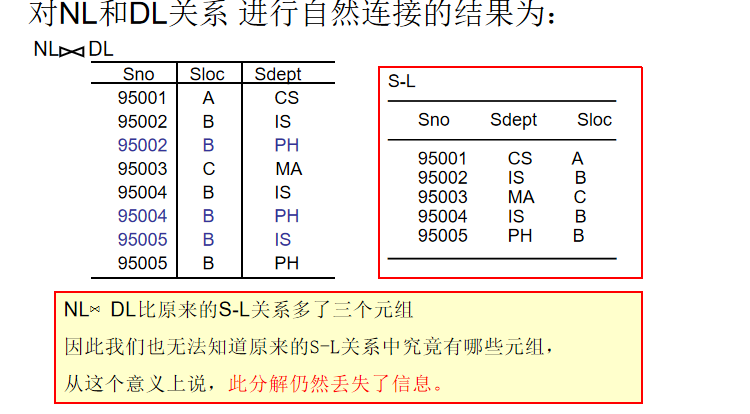
结论： 既不具有无损连接性，也未保持函数依赖。 (这是典型的有损分解)

第三种分解情况

分解方案 ： ND(Sno,Sdept)ND(Sno, Sdept)ND(Sno,Sdept) 和 NL(Sno,Sloc)NL(Sno, Sloc)NL(Sno,Sloc)。这里选择用 SnoSnoSno（学号，即主键）作为公共属性。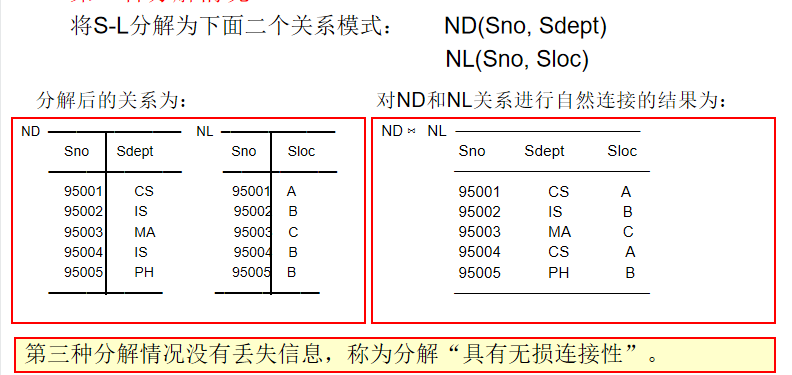

无损连接性： 是满足的。因为 SnoSnoSno 是主键，通过学号确实能把两张表完美地拼回原样，不会多也不会少。
但是原有的依赖 Sdept→SlocSdept \rightarrow SlocSdept→Sloc（系别决定宿舍）丢失了，在 NDNDND 表中，有 (Sno, Sdept)；在 NLNLNL 表中，有 (Sno, Sloc)。
假如 Sdept→SlocSdept \rightarrow SlocSdept→Sloc 规定"CS系必须在A楼"。现在的设计允许在 NDNDND 表里把某学生改成CS系，但在 NLNLNL 表里却忘了把他改到A楼。数据库无法自动检查"CS系对应A楼"这个规则，因为这两个属性分家了。
结论： 具有无损连接性，但未保持函数依赖。 (对于3NF来说，这是不够的)

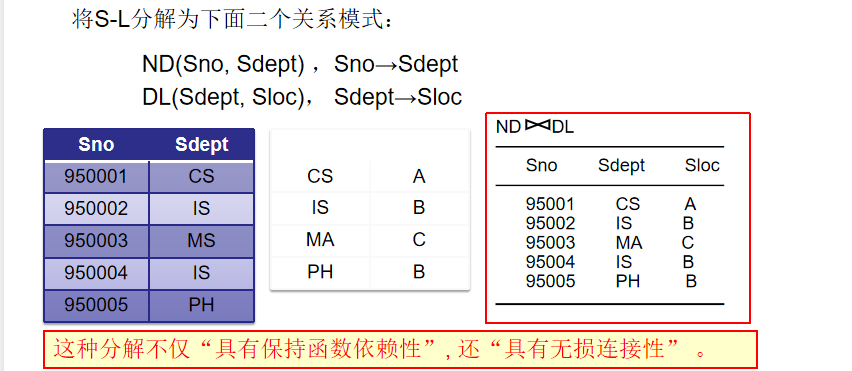
第四种分解情况

分解方案 ： ND(Sno,Sdept)ND(Sno, Sdept)ND(Sno,Sdept) 和 DL(Sdept,Sloc)DL(Sdept, Sloc)DL(Sdept,Sloc)。这里利用传递依赖的中间点 SdeptSdeptSdept 进行切分。

表ND (Sno, Sdept): 这里的 SnoSnoSno 是主键，保留了 Sno→SdeptSno \rightarrow SdeptSno→Sdept。
表DL (Sdept, Sloc): 这里的 SdeptSdeptSdept 是主键，保留了 Sdept→SlocSdept \rightarrow SlocSdept→Sloc。
为什么是完美的分割
- 保持函数依赖： 所有的业务规则都在各自的表中得到了体现。
- 无损连接性： 两个表的公共属性是 SdeptSdeptSdept。在表 DLDLDL 中，SdeptSdeptSdept 是主键（Key）。定理：如果两个表的公共属性是其中一个表的键，那么连接就是无损的。
- 自然连接 ND⋈DLND \bowtie DLND⋈DL 可以完美还原原表 S−LS-LS−L。
结论： 既具有无损连接性，又保持了函数依赖。 这就是标准的第三范式（3NF）分解结果。

分解情况	方案	无损连接性	保持函数依赖	评价
第一种	拆成三个孤立属性	×	×	完全错误，丢失数据关联
第二种	以Sloc(非键)为桥梁	×	×	错误，产生虚假数据
第三种	以Sno为桥梁	√	×	不完美，丢失了 Sdept→SlocSdept \rightarrow SlocSdept→Sloc 的约束，维护困难
第四种	以Sdept为桥梁	√	√	完美，符合3NF标准

2. 无损连接性的检验

当分解多于两个关系时，用这个算法来判断是否为无损连接。

【例题 4】 U=A,B,C,D,E,F=AB→C,C→D,D→EU={A,B,C,D,E}, F={AB\to C, C\to D, D\to E}U=A,B,C,D,E,F=AB→C,C→D,D→E。分解 ρ={R1(ABC),R2(CD),R3(DE)}\rho = \{ R_1(ABC), R_2(CD), R_3(DE) \}ρ={R1(ABC),R2(CD),R3(DE)} 是否为无损连接？

解：

构造初始表 (3行, 5列)：
- AjA_jAj 在 RiR_iRi 中，填 aja_jaj；
- AjA_jAj 不在 RiR_iRi 中，填 bijb_{ij}bij。

关系	A	B	C	D	E
R1(ABC)R_1(ABC)R1(ABC)	a1a_1a1	a2a_2a2	a3a_3a3	b14b_{14}b14	b15b_{15}b15
R2(CD)R_2(CD)R2(CD)	b21b_{21}b21	b22b_{22}b22	a3a_3a3	a4a_4a4	b25b_{25}b25
R3(DE)R_3(DE)R3(DE)	b31b_{31}b31	b32b_{32}b32	b33b_{33}b33	a4a_4a4	a5a_5a5

根据 F 逐一"Chase" (修改 bbb 符号)：

(1) AB →\to→ C ：
- F 要求：A, B 列相同的行，其 C 列也必须相同。
- 表中 R1, R2, R3 在 (A, B) 列上均不相同。无变化。
(2) C →\to→ D ：
- F 要求：C 列相同的行，其 D 列也必须相同。
- R1, R2 的 C 列相同 (都是 a3a_3a3)。
- R2 的 D 列是 a4a_4a4，R1 的 D 列是 b14b_{14}b14。
- 将 b14b_{14}b14 修改为 a4a_4a4。

关系	A	B	C	D	E
R1(ABC)R_1(ABC)R1(ABC)	a1a_1a1	a2a_2a2	a3a_3a3	a4a_4a4	b15b_{15}b15
R2(CD)R_2(CD)R2(CD)	b21b_{21}b21	b22b_{22}b22	a3a_3a3	a4a_4a4	b25b_{25}b25
R3(DE)R_3(DE)R3(DE)	b31b_{31}b31	b32b_{32}b32	b33b_{33}b33	a4a_4a4	a5a_5a5

(3) D →\to→ E：F 要求：
- D 列相同的行，其 E 列也必须相同。
- R1, R2, R3 的 D 列现在相同了 (都是 a4a_4a4)。
- R3 的 E 列是 a5a_5a5。
- 将 b15b_{15}b15 和 b25b_{25}b25 都修改为 a5a_5a5。

关系	A	B	C	D	E
R1(ABC)R_1(ABC)R1(ABC)	a1a_1a1	a2a_2a2	a3a_3a3	a4a_4a4	a5a_5a5
R2(CD)R_2(CD)R2(CD)	b21b_{21}b21	b22b_{22}b22	a3a_3a3	a4a_4a4	a5a_5a5
R3(DE)R_3(DE)R3(DE)	b31b_{31}b31	b32b_{32}b32	b33b_{33}b33	a4a_4a4	a5a_5a5

检查结果：
- R1R_1R1 所在的行变成了 (a1,a2,a3,a4,a5)(a_1, a_2, a_3, a_4, a_5)(a1,a2,a3,a4,a5)。
- 结论：因为出现了全 aaa 的行，所以该分解具有无损连接性。

四、本章小结 (复习要点)

规范化 ：1NF →\to→ 2NF →\to→ 3NF →\to→ BCNF →\to→ 4NF 的过程。
Armstrong 公理系统：3条基本规则（自反, 增广, 传递）+ 3条导出规则。
属性闭包 ( XF+X_F^+XF+) ：必须掌握其计算方法（算法 6.1）。
候选码 ：必须掌握其求解方法（L/R/N/LR 分类法）。
最小依赖集 ( FmF_mFm**)** ：必须掌握其三步求解法（右部分解, 左部去冗余, 依赖去冗余）。
模式分解：
- 两大准则：无损连接性 和 保持函数依赖。
- 必须掌握 无损连接性的 Tableau 检验法。
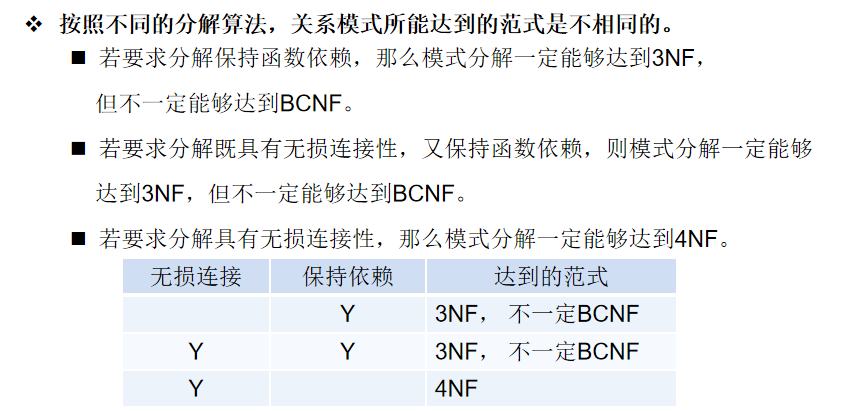
- 理解 3NF（保持FD+无损）和 BCNF（无损, 不一定保持FD）的分解算法及其权衡。