《无线传感器网络》第7讲 定位技术
一、定位概述与意义
- 定义 :确定目标在特定坐标系下的位置。
- 物理位置:具体的坐标数值。
- 符号位置:所在范围的符号表示(如"房间A")。
- 两种意义 :
- 导航:确定自身位置。
- 跟踪:确定目标位置。
- WSN定位的重要性:传感器数据必须附加时空信息才有意义,用于事件地点报告、目标跟踪、协助路由、网络管理和基于位置的服务。
- WSN定位的特点:节点随机部署,需自定位;GPS成本高、功耗大且受环境限制,不适用于所有WSN场景。
二、定位技术性能指标
- 定位精度 :
- 绝对精度 :估计位置与实际位置的最大误差距离。
- 准确率 :满足精度要求的结果占总结果的比例(如:95%准确率下达到20cm精度)。
- 覆盖范围 :定位系统能覆盖的区域面积(如超声波:分米级精度,覆盖十多米;Wi-Fi/蓝牙:3米精度,覆盖100米;GSM:100米精度,覆盖公里级)。
- 刷新速度 :提供位置信息的频率(如GPS每秒1次)。
- WSN相关指标 :
- 代价:硬件和算法成本。
- 锚节点密度:单位面积内已知位置的锚节点数量,影响部署成本和可扩展性。
- 鲁棒性:对环境变化和节点故障的容忍能力。
三、WSN定位算法的设计特点
- 能量高效:计算复杂度低,通信开销小。
- 鲁棒性:容忍节点加入、离开或失效。
- 自组织性:不依赖全局基础设施,适应随机部署。
- 分布计算:节点自行计算自身位置,无需集中处理。
四、计算节点位置的基本方法
1. 三边定位法
- 原理 :已知三个锚节点坐标 (xi,yi)(x_i, y_i)(xi,yi) 及到未知节点D的距离 did_idi,解方程组:
{(x−x1)2+(y−y1)2=d12(x−x2)2+(y−y2)2=d22(x−x3)2+(y−y3)2=d32\begin{cases} (x - x_1)^2 + (y - y_1)^2 = d_1^2 \\ (x - x_2)^2 + (y - y_2)^2 = d_2^2 \\ (x - x_3)^2 + (y - y_3)^2 = d_3^2 \end{cases}⎩ ⎨ ⎧(x−x1)2+(y−y1)2=d12(x−x2)2+(y−y2)2=d22(x−x3)2+(y−y3)2=d32 - 局限 :距离测量存在误差时可能无解或误差大。

2. 极大似然估计法
- 原理 :利用n (n≥3)n\ (n \geq 3)n (n≥3)个锚节点的距离信息,通过最小二乘法求解。
- 步骤 :
- 将方程组转化为线性形式 AX=bAX = bAX=b,其中:
A=[2(x1−xn)2(y1−yn)⋮⋮2(xn−1−xn)2(yn−1−yn)],b=[x12−xn2+y12−yn2+dn2−d12⋮xn−12−xn2+yn−12−yn2+dn2−dn−12],X=[xy]A = \begin{bmatrix} 2(x_1 - x_n) & 2(y_1 - y_n) \\ \vdots & \vdots \\ 2(x_{n-1} - x_n) & 2(y_{n-1} - y_n) \end{bmatrix}, \quad \\b = \begin{bmatrix} x_1^2 - x_n^2 + y_1^2 - y_n^2 + d_n^2 - d_1^2 \\ \vdots \\ x_{n-1}^2 - x_n^2 + y_{n-1}^2 - y_n^2 + d_n^2 - d_{n-1}^2 \end{bmatrix}, \quad X = \begin{bmatrix} x \\ y \end{bmatrix}A= 2(x1−xn)⋮2(xn−1−xn)2(y1−yn)⋮2(yn−1−yn) ,b= x12−xn2+y12−yn2+dn2−d12⋮xn−12−xn2+yn−12−yn2+dn2−dn−12 ,X=[xy] - 使用最小均方误差估计:
X^=(ATA)−1ATb\hat{X} = (A^T A)^{-1} A^T bX^=(ATA)−1ATb
- 将方程组转化为线性形式 AX=bAX = bAX=b,其中:
- 优点 :对测量误差有较好的容错性,精度随锚节点数增加而提高。

3. 三角定位法
- 原理 :已知三个锚节点坐标及未知节点D相对于它们的角度(如∠ADB,∠ADC\angle ADB, \angle ADC∠ADB,∠ADC),通过几何关系(圆心、半径)确定D的位置。
- 步骤 :根据角度确定外接圆圆心和半径,转化为三边定位问题求解。

五、定位算法分类
1. 基于是否测量距离
- 基于距离(range-based):测量节点间实际距离或角度(TOA、TDOA、RSSI、AOA),精度高但对硬件要求高。
- 距离无关(range-free):不测量实际距离,利用网络连通性等信息估算位置(如质心法、DV-Hop),精度较低但成本低。
2. 基于定位次序
- 递增式 (Incremental):从锚节点附近开始 ,逐次向外定位;误差会累积传播。
- 并发式 (Concurrent):所有节点同时计算位置;误差不累积,但协调复杂。
六、基于距离的定位技术 range-base
1. TOA(到达时间法)
TOA Time of Arrival ToA 到达时间法
- 原理 :根据信号传播时间 ttt 和速度 vvv 计算距离d=v⋅td = v \cdot td=v⋅t。
- 要求:收发双方严格时间同步。
- 评价:精度高,但需精确时钟,受环境影响(如声速受温度影响)。
2. TDOA(到达时间差法)
TDOA Time Difference of Arrival TDoA 到达时间差法
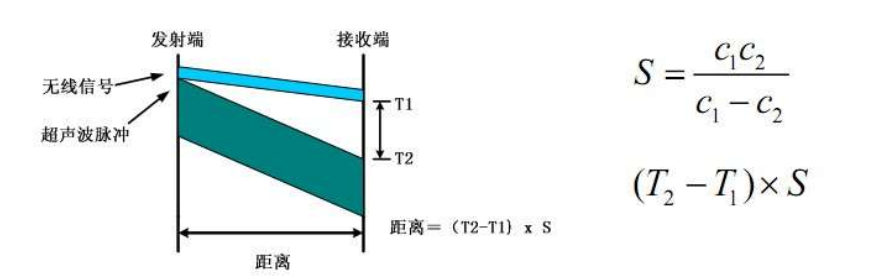
- 原理 :发射节点同时发射两种不同速度的信号 (如无线电和超声波),接收节点根据到达时间差 Δt\Delta tΔt 计算距离:
d=v1v2v1−v2⋅Δtd = \frac{v_1 v_2}{v_1 - v_2} \cdot \Delta td=v1−v2v1v2⋅Δt - 典型应用:MIT的Cricket系统,用于室内房间级定位。
- 优点 :无需时间同步,精度较高。
3. RSSI(接收信号强度指示法)
RSSI Received Signal Strength Indicator 接收信号强度指示法
- 原理 :根据已知的发射功率PtxP_{tx}Ptx和路径损耗模型,由接收功率PrxP_{rx}Prx推算距离。
- 路径损耗模型:Prx∝Ptx/dαP_{rx} \propto P_{tx} / d^\alphaPrx∝Ptx/dα,其中α\alphaα为路径损耗指数。
- 计算公式:d=c⋅PtxPrxαd = \sqrt[\alpha]{\frac{c \cdot P_{tx}}{P_{rx}}}d=αPrxc⋅Ptx 。
- 评价 :无需额外硬件,但误差大(受多径衰落、遮挡、设备差异影响)。
- 典型应用:微软RADAR系统,采用指纹匹配或理论模型。
4. AOA(到达角度法)
AOA Angle of Arrival 到达角度法
- 原理 :通过天线阵列测量信号到达方向,利用几何关系计算位置。
- 角度计算 :通过比较天线间信号相位差 ψ\psiψ计算角度θ\thetaθ:
θ=arccos(ψ⋅λ2πd)\theta = \arccos\left( \frac{\psi \cdot \lambda}{2\pi d} \right)θ=arccos(2πdψ⋅λ)
其中λ\lambdaλ为波长,ddd为天线间距。 - 评价:精度高且有方向信息,但需要天线阵列,硬件成本高。
七、距离无关的定位技术 range-free
1. 质心算法
- 原理 :未知节点将接收到的所有锚节点坐标的平均值 作为自身位置。
(xest,yest)=(∑i=1NxiN,∑i=1NyiN)(x_{est}, y_{est}) = \left( \frac{\sum_{i=1}^N x_i}{N}, \frac{\sum_{i=1}^N y_i}{N} \right)(xest,yest)=(N∑i=1Nxi,N∑i=1Nyi) - 过程 :锚节点周期性广播位置信标;未知节点收到至少 kkk 个不同锚节点信标后计算质心。
- 评价 :简单、分布式、扩展性好;精度取决于锚节点密度和分布。
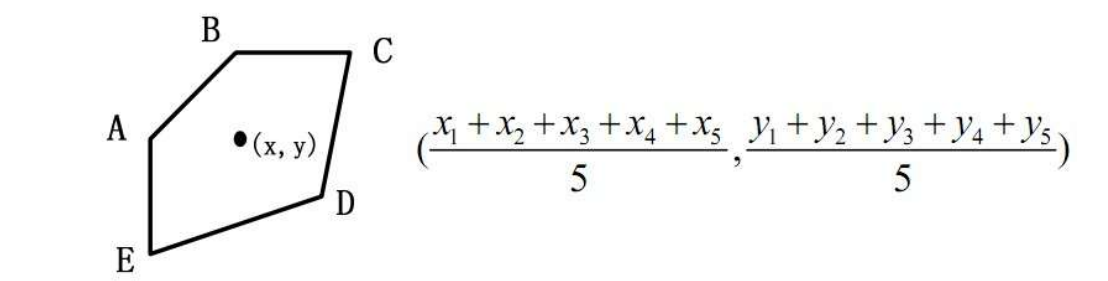
2. DV-Hop算法
-
原理 :通过跳数和平均每跳距离 估算节点间距离,再利用三边或极大似然法定位。
-
三阶段:
-
计算最小跳数 :锚节点洪泛位置信息(跳数字段递增),所有节点记录到各锚节点的最小跳数。
-
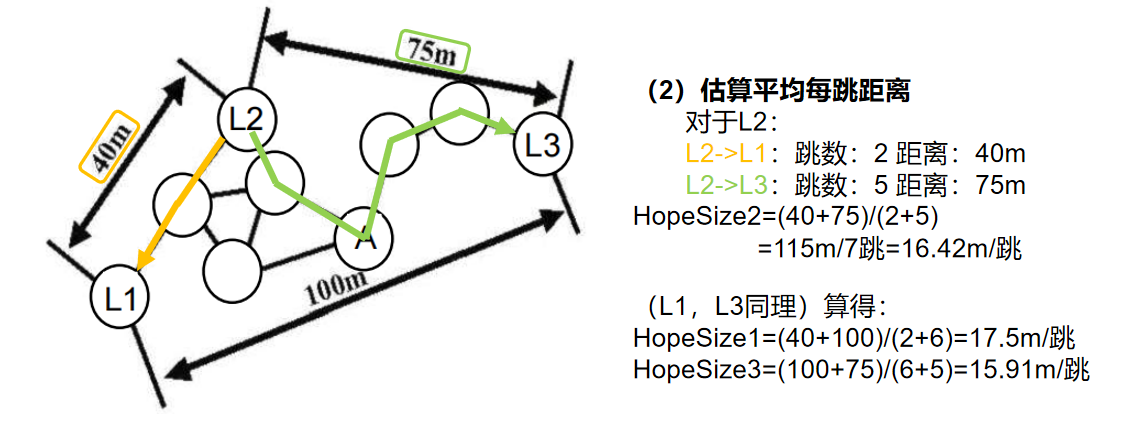
估算平均每跳距离 :每个锚节点根据其他锚节点的已知坐标和最小跳数计算平均每跳距离:
HopSizei=∑j≠i(xi−xj)2+(yi−yj)2∑j≠ihijHopSize_i = \frac{\sum_{j \neq i} \sqrt{(x_i - x_j)^2 + (y_i - y_j)^2}}{\sum_{j \neq i} h_{ij}}HopSizei=∑j=ihij∑j=i(xi−xj)2+(yi−yj)2并广播,未知节点接收并记录最近的锚节点的HopSize。
-
位置估算 :未知节点用最小跳数 × HopSize 估算到各锚节点距离,再用三边或极大似然法计算坐标。
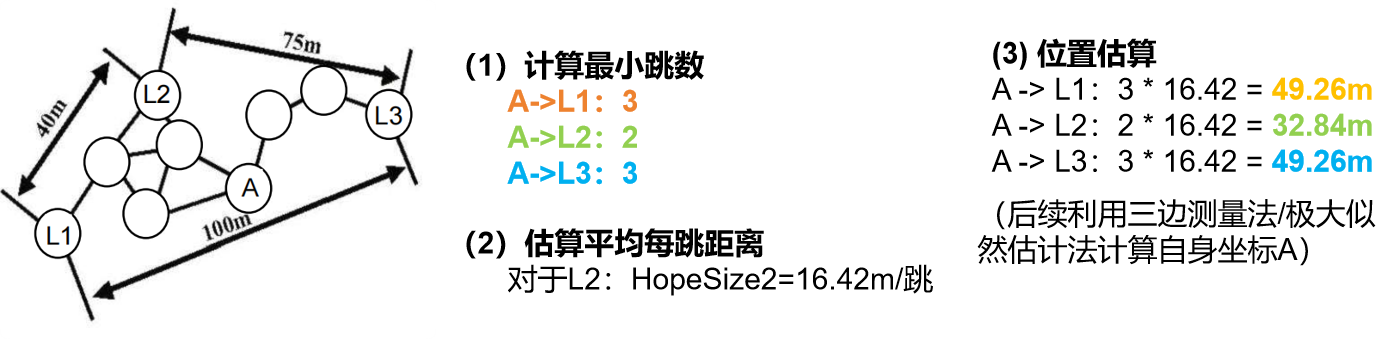
-
-
评价:无需测距硬件,实现简单;但用跳段距离代替直线距离会引入误差。
八、两种定位技术对比
| 特性 | 基于距离 range-base | 距离无关 range-free |
|---|---|---|
| 精度 | 较高(厘米-米级) | 较低(米-数十米级) |
| 硬件要求 | 高(需专用测距模块) | 低(仅需通信模块) |
| 能耗 | 高(测距过程耗能) | 低 |
| 环境影响 | 大(受环境干扰明显) | 小 |
| 典型算法 | TOA, TDOA, RSSI, AOA | 质心法, DV-Hop |
| 适用场景 | 对精度要求高的应用(如跟踪) | 成本敏感、精度要求低的应用(如环境监测) |
九、公式总结
- 三边定位方程组:基于圆的方程
- 极大似然估计矩阵形式 :X^=(ATA)−1ATb\hat{X} = (A^T A)^{-1} A^T bX^=(ATA)−1ATb
- TDOA距离公式 :d=v1v2v1−v2⋅Δtd = \frac{v_1 v_2}{v_1 - v_2} \cdot \Delta td=v1−v2v1v2⋅Δt
- RSSI距离估算 :d=c⋅PtxPrxαd = \sqrt[\alpha]{\frac{c \cdot P_{tx}}{P_{rx}}}d=αPrxc⋅Ptx
- AOA角度计算 :θ=arccos(ψ⋅λ2πd)\theta = \arccos\left( \frac{\psi \cdot \lambda}{2\pi d} \right)θ=arccos(2πdψ⋅λ)
- 质心坐标:所有锚节点坐标的算术平均
- DV-Hop平均每跳距离 :HopSizei=∑锚节点间实际距离∑对应跳数HopSize_i = \frac{\sum \text{锚节点间实际距离}}{\sum \text{对应跳数}}HopSizei=∑对应跳数∑锚节点间实际距离
习题
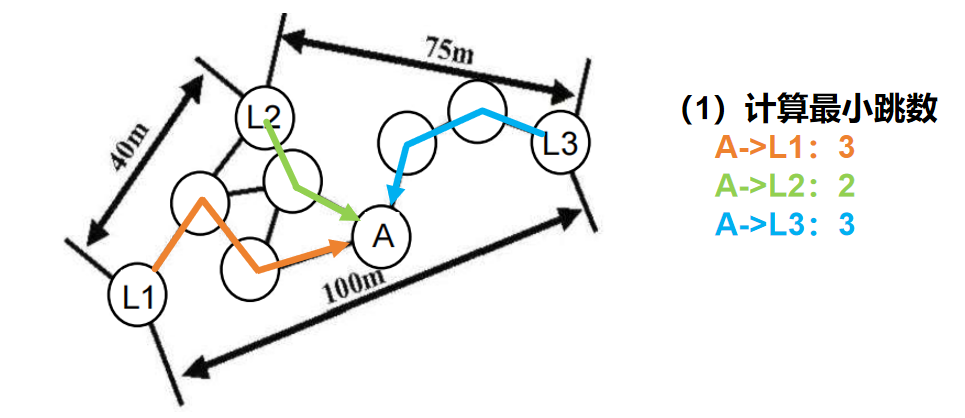
- (填空题) 已知一个网络的拓扑结构如下图所示。L1、L2、L3为锚节点。使用DVHOP算法确定网络中所有非锚节点的位置。
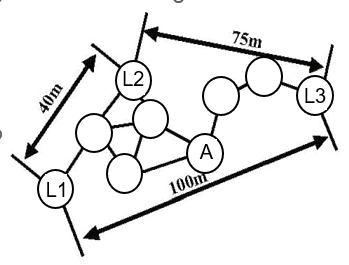
(1)针对未知节点A,它距离三个锚节点的最小跳数分别是:
距离L1__3__跳;
距离L2__2__跳;
距离L3__3__跳。
(2) 锚节点L1,计算得到的平均每跳距离为__17.5__米;(保留小数点后1位)
锚节点L3,计算得到的平均每跳距离为__15.9__米;(保留小数点后1位)
(3)假设节点A最先得到了锚节L3广播的平均每跳距离,则节点A计算得到的三个跳段距离分别为:
距离锚节点L1的跳段距离是___47.7___米;
距离锚节点L2的跳段距离是___31.8___米;
距离锚节点L3的跳段距离是___47.7___米。
- (填空题) 如果节点A与节点B的实际距离位20米,某方法对A与B的估计距离为18米,则方法的定位绝对精度是__2__米。
本题中:绝对精度 = 20 - 18 = 2m
定位精度:
- 绝对精度 :估计位置与实际位置的最大误差距离。
- 准确率 :满足精度要求的结果占总结果的比例(如:95%准确率下达到20cm精度)。
- (单选题) 基于通信距离的(range-based)定位技术中,需通过 "发射两种不同传播速度的无线信号,利用信号到达时间差计算距离" 的是(B)
A. TOA(Time of Arrival)
B. TDOA(Time Difference of Arrival)
C. RSSI(Received Signal Strength Indicator)
D. AOA(Angle-of-Arrival)