摘要
本周首先学习了f-散度族的相关知识,了解了KL散度、JS散度与总变分距离的数学表示与性质,同时对上周学习的 Wasserstein 距离进行了回顾,并比较了 Wasserstein 距离与它们的优缺点;其次,对前面了解过的激活函数进行了总结,系统地了解了它们的公式与图像等。
Abstract
This week, I first studied the family of f-divergences, learning the mathematical expressions and properties of KL divergence, JS divergence, and total variation distance. I also reviewed the Wasserstein distance covered last week and compared the advantages and disadvantages of Wasserstein distance with those of the f-divergences. Secondly, I summarized the activation functions I had previously studied, systematically reviewing their formulas and graphical representations.
1 Wasserstein 距离(续)
本节主要基于上周对 Wasserstein 距离的学习,将它与其他散度进行对比。
1.1 Wasserstein 距离回顾
Wasserstein距离,也称为推土机距离,是一种度量两个概率分布之间距离的方法,通常代表最低的总运输成本。
给定两个分别定义在空间 X 和 Y 上的概率分布 P 和 Q,以及一个连续成本函数 c(x,y) 表示将单位质量从位置 x 移动到 y 的成本。 对于这两个概率分布,p 阶 Wasserstein 距离的数学表示如下:
当 X 和 Y 是欧几里得空间时,代价函数是两点间距离的 p 次方,即 ,这也代表,p 是调节敏感性的连续参数能够决定对长距离运输的惩罚方法。
在实际应用中,p 值为 1 和 2 最为常见,具体选择取决于问题的需求。前者使用线性惩罚,运输成本与距离成正比,更适合存在噪声或异常值的场景,故广泛用于稳健统计和生成模型训练;二阶距离则在需要精确匹配的物理建模和几何分析中更有优势,因为它使用平方惩罚,更加强调长距离运输的成本,能够更好地区分具有相似主体但尾部不同的分布。
1.2 其他散度及对比
1.2.1 KL散度
KL散度(Kullback-Leibler Divergence)衡量的是使用一个分布 Q 来近似真实分布 P 时,所损失的信息量,若 P、Q 为离散分布,则它的表示为:
若为连续分布,则它的表示为:
同时对于以上表示均约定:
它的基本性质包括:
非负性,,只在 P 与 Q 几乎处处相等时取等号;
非对称性,,这也是KL散度最重要的特征之一,决定了它的两种形式有不同的应用场景;
不满足三角不等式(),因此它不是真正的度量,只是一个散度。
p.s. 度量是一个严格定义的数学概念,用于衡量空间中任意两点之间的距离,散度则更为宽松,用于衡量两个对象(尤其是概率分布)差异。
KL散度的典型应用包括变分推断、期望最大化算法、信息论。
1.2.2 JS散度
JS散度(Jensen-Shannon Divergence)是KL散度的对称化和平滑版本,它的表示如下:
其中 ,它是 P 和 Q 的中间分布。
上式可展开为:
可以清晰地观察到,JS散度具有对称性。这是它相对于KL散度的最主要改进。
它的取值范围在 [0,log2] 之间,当且仅当 P 与 Q 几乎处处相等取下界 0,当 P 和 Q 的支撑集完全不相交时取上界 log2。
同时JS散度也不满足三角不等式,不是真正的度量,只是一个散度。
JS散度是原始 GAN 的判别器损失的理论基础,不过效果不好,因为当它取上界时梯度会消失,导致原始 GAN 训练崩溃。
1.2.3 总变分距离
总变分距离(Total Variation Distance)衡量的是两个概率分布在所有可能事件上概率差异的最大值。对于定义在同一个概率空间上的两个概率分布 P 和 Q ,它的数学表示如下:
其中 A 是任意一个事件, 是所有可测事件的集合。
对于离散分布,上式等价于:
而对于连续分布,则等价于:
它不同于前两者仅是散度,而是一个真正的度量,满足所有距离公理。其取值范围为 [0,1] 。当两个分布完全相同时取下界 0 ,当两个分布支撑集完全不相交时取上界 1。
这是一个大家族,KL散度、JS散度都是其特例。
-
定义:Df(P∣∣Q)=∫q(x)f(p(x)q(x))dxDf(P∣∣Q)=∫q(x)f(q(x)p(x))dx,其中 ff 是凸函数。
-
共同特性 :都是散度 (非对称),且不依赖于样本空间的几何,只关心密度比。因此,与Wasserstein有根本的不同。
1.2.4 总结与对比
上面的KL散度、JS散度与总变分距离都是同一个"大家族"的特例,即 f-散度族(f-Divergences)。这是一类用于衡量两个概率分布之间差异的函数,它们都基于一个共同的数学形式。
离散情况下:
连续情况下:
其中要求 为凸函数,且
.
并约定:1. ;2.
。
它们(主要是前面学习的三种)与 Wasserstein 距离的主要对比如下:
-
Wasserstein 距离与总变分距离都是度量,而KL散度与JS散度都只是散度;
-
Wasserstein 距离连续且考虑几何依赖,而另三者均不连续与不考虑;
-
KL散度对于支撑集不重叠的响应是无穷大的,JS散度则会饱和为常数导致梯度消失,总变分距离也有可能为常数,Wasserstein 距离则能够平滑变化;
-
Wasserstein 距离与总变分距离的计算复杂度都很高,前者需解最优传输,后者在高维下十分难求,而KL散度与JS散度的计算复杂度都较低;
5.Wasserstein 距离与KL散度均无界,JS散度与总变分距离都有界。
总而言之,Wasserstein 距离关心的是如何把一个分布变成另一个分布,而另三者都更关心l两个分布每一点是否相同。在机器学习中,若使用后面这类散度或度量作为损失函数,当生成分布与真实分布没有重叠或重叠可忽略时,梯度会消失或爆炸,导致训练失败,而这在训练初期十分常见;若使用 Wasserstein距离作为损失函数,即使分布没有重叠,它也能提供一个平滑的、有意义的梯度来指导生成器稳定改进。
2 激活函数总结
激活函数是神经网络中的非线性变换单元。它的核心作用包括引入非线性**,**使神经网络能够逼近任意复杂函数,从而超越线性模型;控制信息流动,即决定神经元是否激活及激活程度,形成网络的分层抽象能力;通过输出范围控制影响梯度传播和参数更新进而稳定训练过程。其种类大致可分为饱和型激活函数、非饱和型激活函数、自适应门控型激活函数等(下面总结的一般包括整个函数族)。
2.1 饱和型激活函数
饱和型激活函数是指其在输入达到一定阈值后,输出变化率显著下降,呈现饱和状态,输出范围严格有界的激活函数,主要包括 Sigmoid 与 Tanh。
2.1.1 Sigmoid
标准 Sigmoid 函数通常也被称为 Logistic 函数,其数学公式为:
它主要通过指数函数的非线性压缩,将输入映射到 (0, 1) 的输出范围内,图像如下:
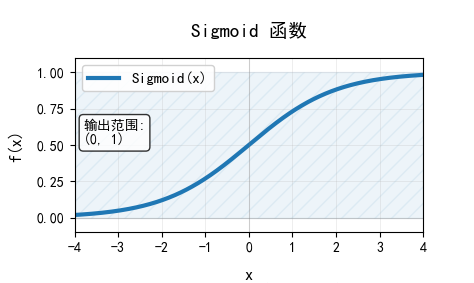
它的输出可以被解释为概率,适合二分类的输出层。但当输入很大或者很小时,曲线平滑,梯度趋近于 0 ,会导致深层网络训练困难;非零中心化,所有权重梯度符号一致会导致后续神经元的梯度更新呈之字形路径,收敛缓慢;同时涉及指数运算,计算开销会比较大。
2.1.2 Tanh
Tanh 函数,即双曲正切函数,其数学公式为:
它同样基于指数函数的非线性压缩,但输出以0为中心,范围为(-1,1),图像如下:
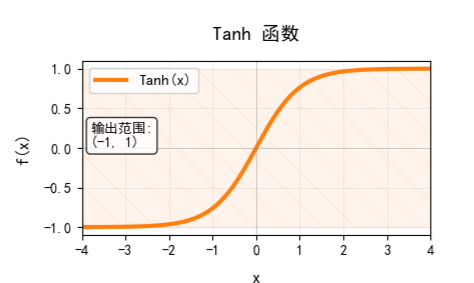
它本质上是缩放平移的 Sigmoid,但相对于 Sigmoid 改善了非零中心化的缺点,有助于梯度流动,收敛速度比 Sigmoid 更快。其梯度消失问题也比 Sigmoid 要好,但依然存在。而且同样涉及指数运算,计算开销较大。
2.2 非饱和型激活函数
非饱和型激活函数的输出范围单侧有界,主要指得就是 ReLU。
其中标准ReLU也被叫做修正线性单元,其数学公式为:
它采用单侧抑制与分段策略。正输入线性通过,负输入则直接置零,输出范围为 ,其图像如下:
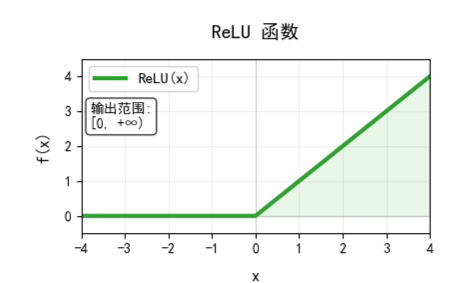
其优点在于能够有效缓解梯度消失,因为正区间梯度恒为 1;计算无需指数运算,比较高效;采用稀疏激活策略,负输入输出 0,更具鲁棒性。缺点在于其输出范围同样非负且无上界,重要的是它会产生神经元死亡的问题,即若某神经元在大量训练数据中始终输出负值,其梯度将永远为0,导致该神经元死亡。
ReLU的一个常见变体就是 Leaky ReLU ,其公式为:
其中 是一个很小的正数。
这个变体主要就是对 ReLU 的负区间进行微小调整,赋予一个很小的斜率 ,使负区间梯度不再恒为 0。其输出范围为
,但负值非常小,其图像如下:
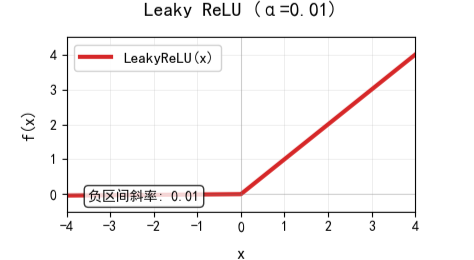
也由此可以看出 Leaky ReLU 解决了神经元死亡(Dying ReLU)的问题 ,因为它的负区间仍有微小梯度,确保神经元始终可被更新;但随之而来也产生了新的问题,即最佳 值需要调参才能得到;且它仍非严格的零中心化
2.3自适应与门控型激活函数
自适应与门控型激活函数通过基于输入值动态调节的门控机制,实现了激活程度的自适应控制,在保持非单调性、处处平滑的同时,显著提升了深层网络的表达能力和训练稳定性。
2.3.1 GELU
GELU(高斯误差线性单元)是一种独特的非饱和门控型激活函数,主要通过概率门控实现自适应激活,是Transformer的标准选择。其数学公式为:
其中, 指的是标准正态分布的累积分布函数。
它基于神经元的随机正则化,根据输入值大小决定激活概率,输出范围近似为 ,其图像为:
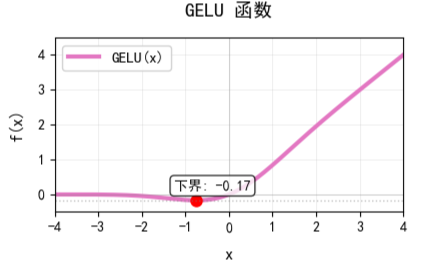
它能够根据输入置信度调整输出幅度,提供丰富的非线性表达能力,训练稳定,适合深层架构,但计算开销大,实际上通常使用近似公式,存在微小误差,且基于正态分布假设,不一定适用所有数据分布。
2.3.2 Swish
Swish 是自门控函数的原型,其公式如下:
其中 可以固定也可以通过学习得到,应用中通常取 1,此时其输出范围约为
,其图像如下:
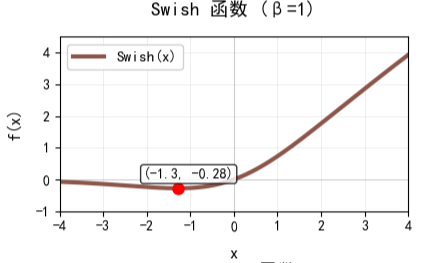
它主要通过 Sigmoid 门控机制来进行调节。当 x 为很大的正数时,趋近于线性;当 x 为负数时则会平滑地衰减到接近 0。由此,Swish在深层网络中有时表现会优于 ReLU,但计算量会稍大
2.3.3 Mish
Mish 函数的数学公式如下:
其中 softplus 函数公式为 ,确保正性且平滑。
它主要通过双曲正切门控实现自适应调节,输出范围约为 ,图像如下:
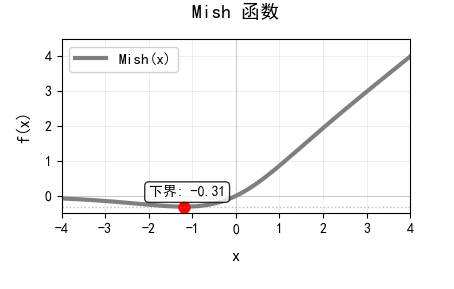
它相比ReLU,能够完全消除神经元死亡问题,能够在避免梯度消失的同时提供自正则化效果,但涉及运算较多,计算成本最高。
2.4 输出层专用激活函数
输出层专用激活函数主要就是 softmax,其公式为:
它通过对所有输入进行指数归一化,使每个输出都在(0,1)范围内,且所有输出之和为 1,能够形成完整的概率分布。
由于其归一化特性,它成为天然的多分类输出层选择,输出可直接解释为类别概率。也因此,若将它作为隐藏层的激活函数,会破坏特征独立性,导致多特征同时存在的关键信息丢失,同时计算代价高,优化困难。
3 总结
本周首先了解了各种散度的相关知识,并与 Wasserstein 距离进行了对比,其次对以前接触的激活函数进行了总结与拓展,在加深前面理解的同时也了解了新的激活函数,如Swish,对各激活函数如何控制输出范围进行了更加系统的学习。