OpenGL 坐标映射

OpenGL 渲染管线中坐标变换的完整流程

局部坐标 → 世界坐标

世界坐标 →观察坐标

观察坐标 →裁剪坐标

裁剪坐标 → NDC

NDC → 窗口坐标

窗口坐标 → 屏幕坐标

其中局部坐标到裁剪坐标的转换都是由顶点着色器实现的，裁剪坐标到窗口坐标的转换由 OpenGL 固定管线完成，窗口坐标到屏幕坐标的转换则由窗口系统（Glfw / Qt / SDL 等）完成。

局部坐标，顶点相对于模型自身中心的原始坐标。
世界坐标，模型在虚拟世界中的位置。
观察坐标，又称视图坐标，模型相对于摄像机的位置
裁剪坐标，又称投影坐标，应用投影变换后的坐标，听起来像句废话，在本篇文章里，我们将会介绍透视投影和正交投影，到时候读者便能理解什么是投影坐标了。我们现在只需要知道它包含了一个 w 分量，在 [-w, w] 之外的值，我们可以认为在视野之外，会被裁剪掉，然后在投影坐标转 NDL 坐标这一步，会将 (x,y,z)除以w分量（透视除法），把坐标标准化到[-1,1]范围的立方体空间。
NDC（标准化设备坐标），坐标归一化，映射到 [-1,1]。

在一些资料里，我们还会看到一个名词---齐次坐标。在 OpenGL 和计算机图形学中，齐次坐标通常表示为 (x, y, z, w)。也就是在三维坐标的基础上增加了一个 w 分量。

当 w 等于 0 时，它表示的是一个向量（方向），当 w 不等于 0 时，他表示的是一个点。

在顶点着色器之后，图形管线会自动执行透视除法（即 (x/w, y/w, z/w)），以实现在透视投影中物体近大远小的效果。简单来说，它就是三维坐标，加上了一个 w 分量。

接下来，我们再来介绍下透视投影和正交投影，通过对透视投影和正交投影的学习，我们可以了解什么是投影变换，为什么要做投影变换，以及 w 分量的值是怎么来的。

透视投影

我们先来看下透视投影的计算公式，然后再来介绍下这个公式怎么来的。在透视投影中，w 一般设置它的值为 -z。这样 x, y 在裁剪空间（裁剪坐标所在的空间）的大小会和距离成反比，距离越远，数值越小，这是符合我们的实际视觉感受到的效果的。

cpp 复制代码

// 焦距
float f = cot(fov / 2.0f) = 1.0f / tan(fov / 2.0f);
// 屏幕比例
float aspect = width / height;
// 深度映射
float A = (far + near) / (near - far);
float B = (2.0f * far * near) / (near - far);
x_clip = x_view * (f / aspect) ;
y_clip = y_view * f;
z_clip = A * z_view + B;
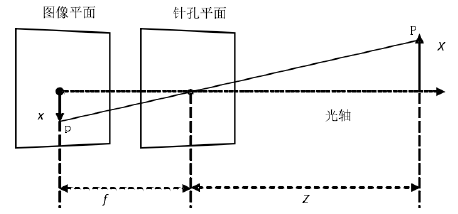
w_clip = -z_view;

OpenGL 透视投影和小孔成像是类似的（参考下图）。

其中 fov 表示视野角度，控制能看到多大范围，OpenGL 最终要将值映射到 [-1, 1] 的范围内的，所以对边长为 1，邻边则是 f ，得出 float f = cot(fov / 2.0f) = 1.0f / tan(fov / 2.0f)。

再根据三角形相似，物体在成像平面的高度为 h * f / d，这个 d 即为 x 到小孔的距离。除以 d 这一步 OpenGL 帮我们做了，我们设置 w_clip 等于 -z_view，OpenGL 在把投影坐标转 NDC 时会除以 w_clip，至于为什么是 -z_view，因为相机是从 (0, 0, 0) 往 -z 方向看的。

到了这里，我们得出第一步公式 x_clip = x_view * f 和 y_clip = y_view * f 。

那么 x 的投影计算公式为什么还有个 aspect 呢？这个很好理解，因为 NDC 坐标空间是正方形的，而窗口不一定是，所以需要有个宽高比去修正。

接下来，我们再来看下 z 分量的投影坐标计算公式

cpp 复制代码

float A = (far + near) / (near - far);
float B = (2.0f * far * near) / (near - far);
z_clip = A * z_view + B;

其中 near 表示最近的可渲染平面，far 表示最远可渲染平面。

我们首先需要了解下 z 这个值是用来干嘛的，z 不就是用来表示物体到相机的距离吗？但是我们屏幕的坐标是二维的，它是不需要深度信息的。不过我们仍需要知道物体距离相机远近，当多个物体在二维坐标下的点相同时，我们应该显示近的物体，因为它会遮挡远的物体。另外 x，y 的 NDC 坐标和 z 都是 1 / z 的关系，那么 z 的 NDC坐标是不是也应该如此呢？

对于近处：物体细节多，需要精确遮挡测试，远处：物体细节少，遮挡关系没有那么重要，刚好 1 / z 可以满足这样的需求，当 z 的绝对值较小时，较小的变化会引起 1 / z 较大幅度的变换，而 z 的绝对值较大时，它的变化影响不是那么大。

根据这样的思路我们得出了一个式子 z_clip = B，B 为常数。转成 NDC 即为 z_ndc = B / z_view。NDC 需要将坐标映射到 [-1, 1] ，显然 B / z_clip 不满足这样的条件，所以我们还得加上一个系数 A ，让它的值域在 [-1, 1] 之间，最终得出式子 z_ndc = A + B / z_view 也就是 z_clip = A * z_view + B

刚刚我们提到"当多个物体在二维坐标下的点相同时，我们应该显示近的物体"，这个过程称为深度测试，深度测试为每个像素维护一个深度缓冲区（Depth Buffer，也称 Z-Buffer），存储该像素的深度值（通常是视角到物体的距离）；绘制时，新像素的深度值与缓冲区中已有值比较，仅当满足预设条件时，才更新颜色缓冲区和深度缓冲区。默认情况新深度 < 存储深度会通过测试。根据深度测试的更新逻辑，我们可以得出一个方程，当 z_view 等于 -near 时 z_ndc 应该等于 -1 ， z_view 等于 -far 时 z_ndc 应该等于 1。解方程得到 A = (far + near) / (near - far), B = (2.0f * far * near) / (near - far)。

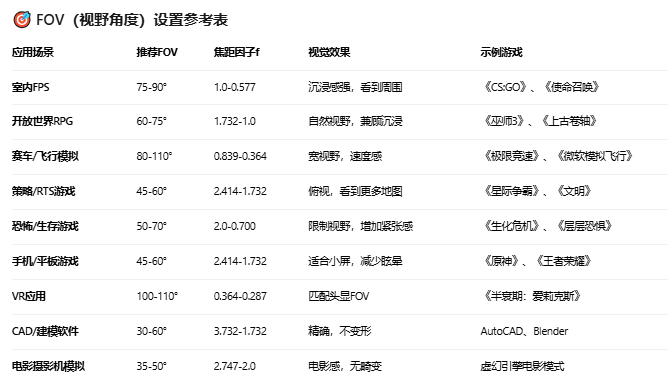
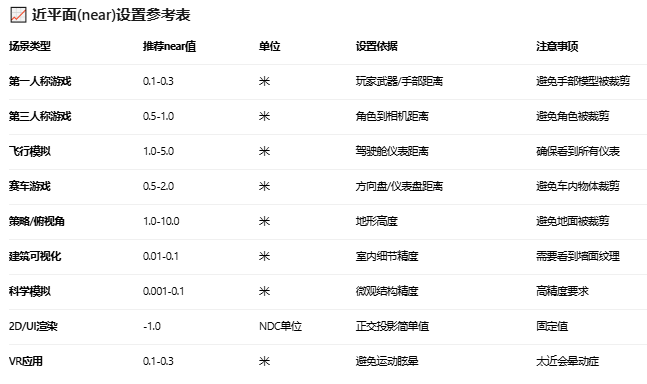
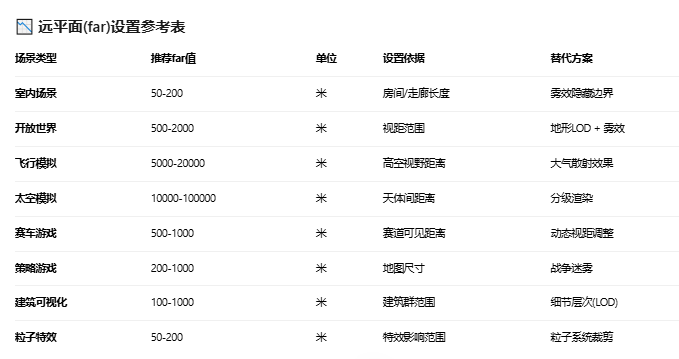
至于 fov，far near 应该怎么设置需要根据实际渲染需求来确定。

正交投影

正交投影得特点是，无近大远小效果，平行投影（所有投影线平行），保持物体实际尺寸。常用于2D、UI、CAD。因为无近大远小效果，它的 w 值恒定为 1。

所以它的公式推导也简单得多，以 x 为例子：x_ndc = x_clip = A * x_view + B

然后根据边界条件，当 x_view 等于裁剪空间左边界 l （视图坐标）时，x 等于 -1，当 x_view 等于右边界 r 时，x 等于 1。根据这个方程，我们可以解出

x = 2 × x_view / (r - l) - (r + l) / (r - l)

y z 同理，最后我们得到正交投影计算公式

cpp 复制代码

x_clip = 2 × x_view / (r - l) - (r + l) / (r - l)
y_clip = 2 × y_view / (t - b) - (t + b) / (t - b)
z_clip = -2 × z_view / (f - n) - (f + n) / (f - n)
w_clip = 1.0

由于笔者水平有限，错误不足之处，烦请各位读者斧正。