一、研究背景
该研究针对非平稳、非线性信号处理 中的模态混叠和参数选择困难问题,提出了一种基于RIME优化算法的VMD方法,用于自适应确定VMD的关键参数(模态数K和惩罚因子α),从而提高信号分解的准确性和效率,并结合小波阈值降噪实现信号去噪。
二、主要功能
- RIME优化VMD参数:自适应选择最优的K和α。
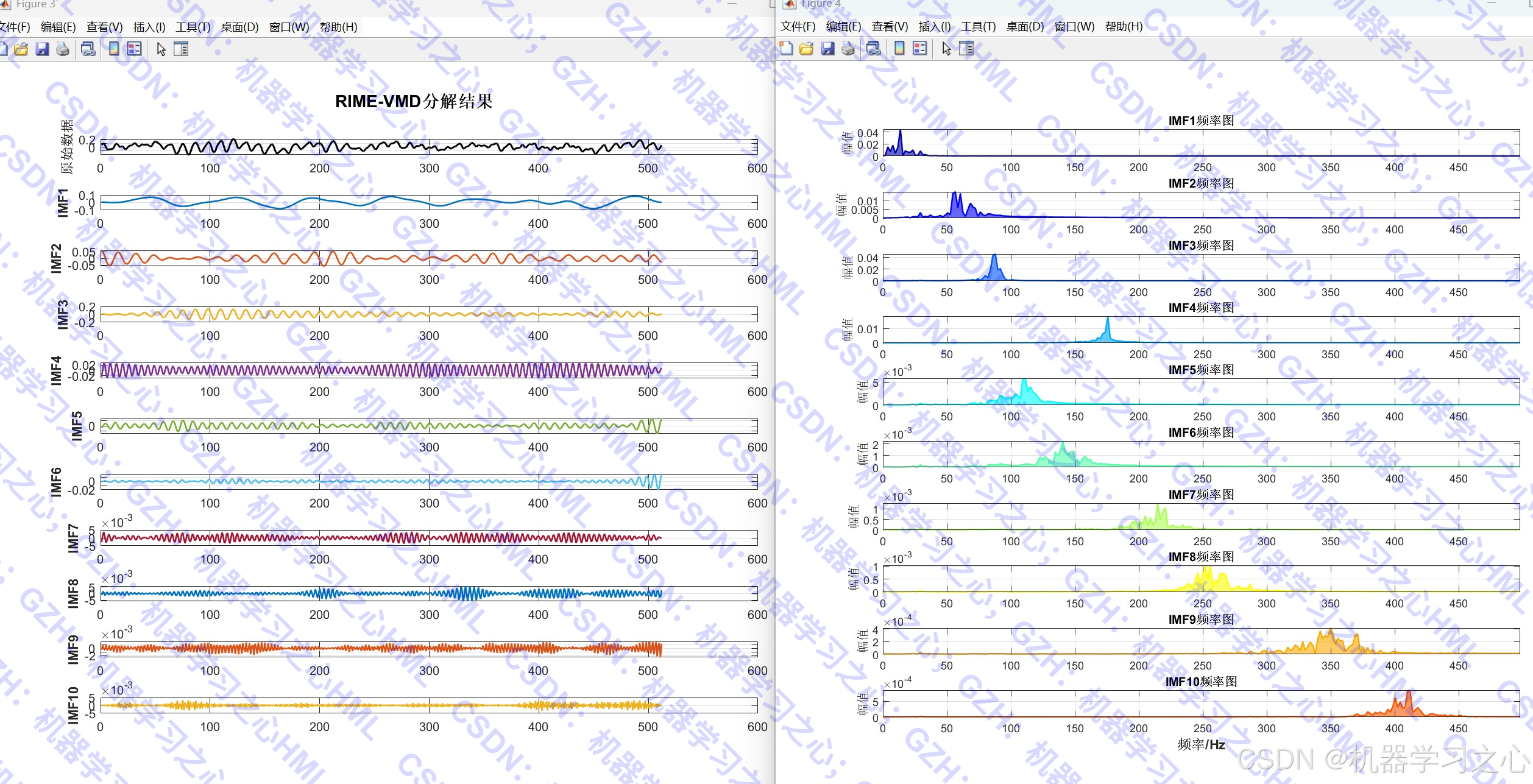
- 信号分解:将原始信号分解为多个IMF(本征模态函数)。
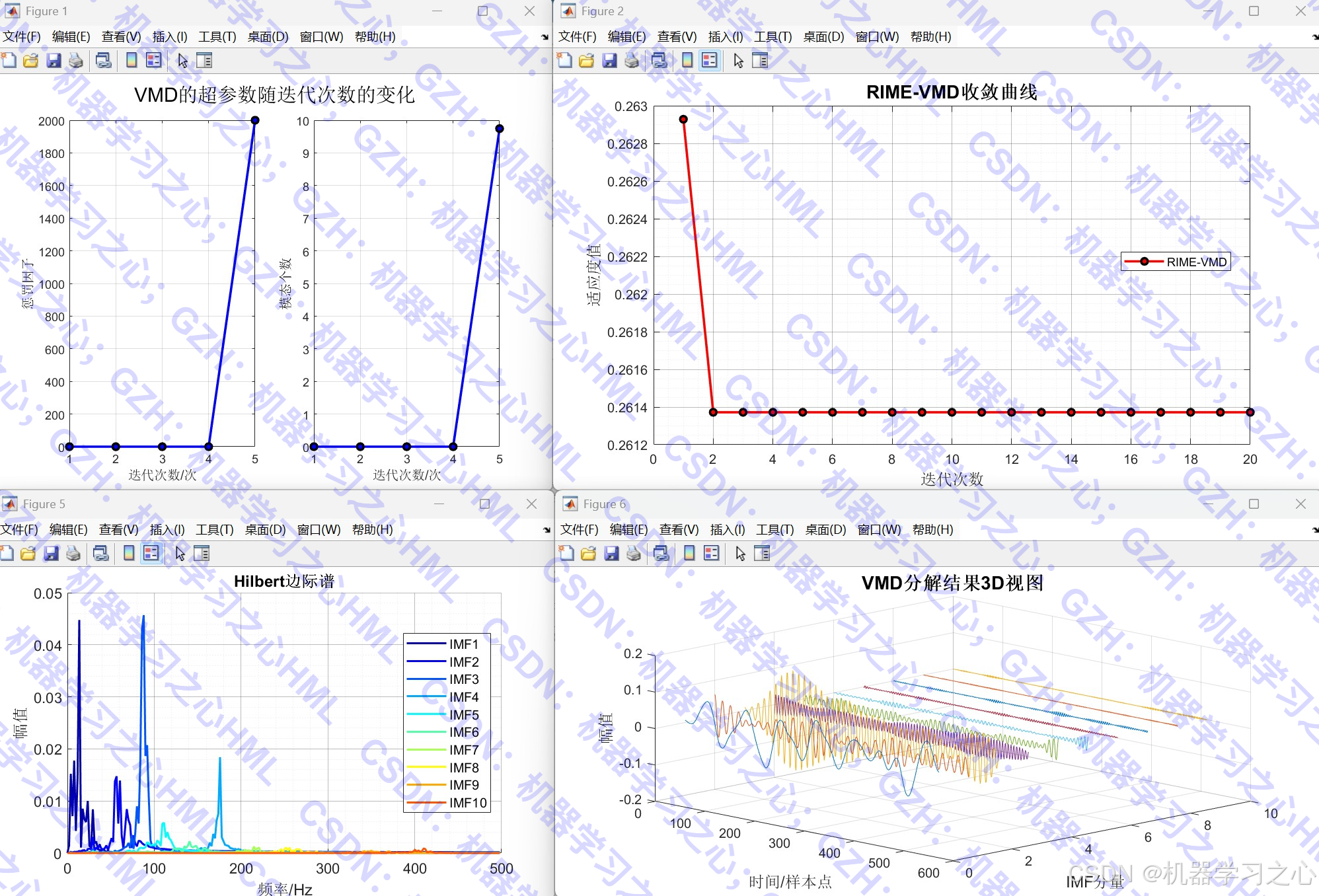
- 频谱分析与边际谱:绘制各IMF的频谱图和Hilbert边际谱。
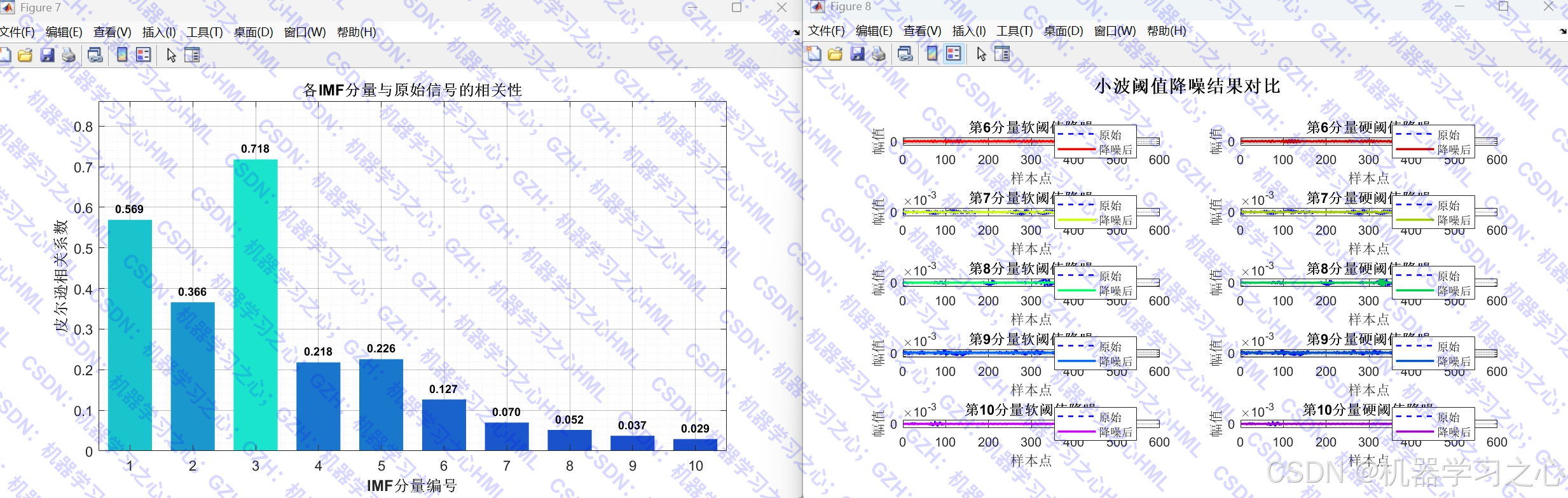
- 相关性分析:计算各IMF与原始信号的皮尔逊相关系数。
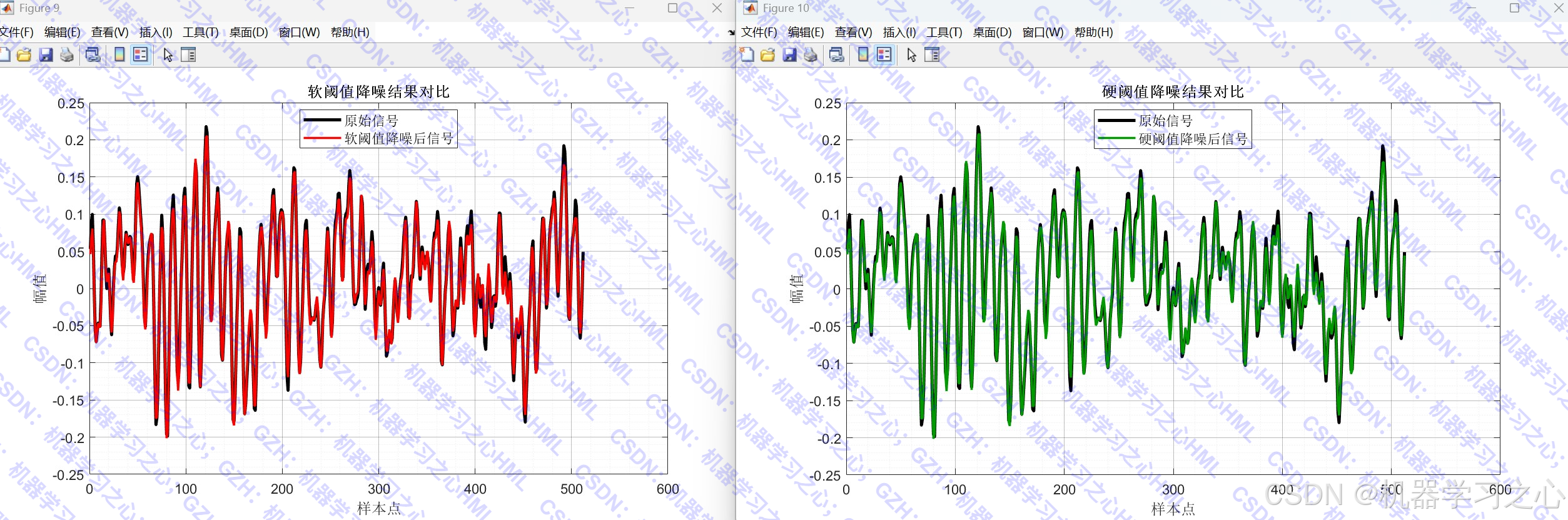
- 小波阈值降噪:对相关性较低的IMF进行软/硬阈值降噪。
- 信号重构:将降噪后的IMF与保留的IMF重构为去噪信号。
- 可视化输出:包括收敛曲线、分解结果、频谱图、3D视图、相关系数图、降噪对比图等。
三、算法步骤
- 数据导入与预处理:读取Excel数据,设置采样频率。
- RIME优化VMD :
- 初始化RIME算法参数。
- 以包络熵或类似指标为适应度函数,优化K和α。
- VMD分解:使用优化后的参数进行信号分解。
- 频域分析:对每个IMF进行FFT,绘制频谱和边际谱。
- 相关性分析:计算各IMF与原始信号的相关系数,设定阈值筛选需降噪的IMF。
- 小波降噪:对筛选出的IMF进行小波软/硬阈值降噪。
- 信号重构与对比:重构降噪信号,并与原始信号对比。
四、技术路线
数据输入 → RIME优化VMD参数 → VMD分解 → 频域分析 → 相关性筛选 → 小波降噪 → 信号重构 → 结果输出五、公式原理
1. VMD原理:
VMD通过变分框架将信号( f(t) )分解为K个模态函数( u_k(t) ):
min{uk},{ωk}{∑k∥∂t[(δ(t)+jπt)∗uk(t)]e−jωkt∥22} \min_{ \{u_k\},\{\omega_k\} } \left\{ \sum_k \left\| \partial_t \left[ \left( \delta(t) + \frac{j}{\pi t} \right) * u_k(t) \right] e^{-j\omega_k t} \right\|_2^2 \right\} {uk},{ωk}min{k∑ ∂t[(δ(t)+πtj)∗uk(t)]e−jωkt 22}
约束条件:
∑kuk=f\sum_k u_k = f∑kuk=f
2. RIME优化算法:
RIME是一种基于冰霜生长过程的元启发式优化算法,用于最小化目标函数(如包络熵)。
3. 小波阈值降噪:
- 软阈值:ηs(x)=sign(x)(∣x∣−T)\eta_s(x) = \text{sign}(x)(|x| - T)ηs(x)=sign(x)(∣x∣−T)
- 硬阈值:ηh(x)=x⋅I(∣x∣>T)\eta_h(x) = x \cdot I(|x| > T)ηh(x)=x⋅I(∣x∣>T)
六、参数设定
| 参数 | 说明 |
|---|---|
fs |
采样频率,默认为1024 Hz |
tau |
噪声容限,默认为0 |
DC |
是否包含直流分量,默认为0 |
init |
初始化方式,默认为1(均匀初始化) |
tol |
收敛容忍度,默认为1e-7 |
wname |
小波基函数,默认为'db1' |
lev |
小波分解尺度,默认为2 |
七、运行环境
- 平台:MATLAB(建议R2020以上)
- 依赖工具箱 :
- Signal Processing Toolbox
- Wavelet Toolbox
- 数据格式 :Excel文件(
data.xlsx,单列信号数据)
八、应用场景
- 机械故障诊断:轴承、齿轮振动信号分析。
- 生物医学信号处理:心电(ECG)、脑电(EEG)信号去噪与特征提取。
- 语音信号处理:语音增强与音素分离。
- 电力系统分析:电能质量扰动检测与分类。
- 地震信号处理:地震波分离与去噪。
- 金融时序分析:股价序列分解与趋势提取。