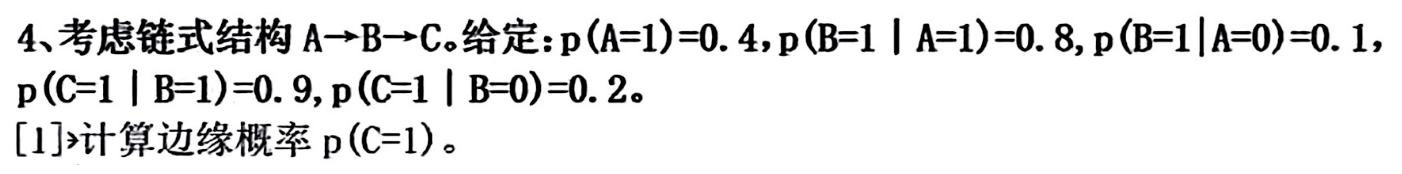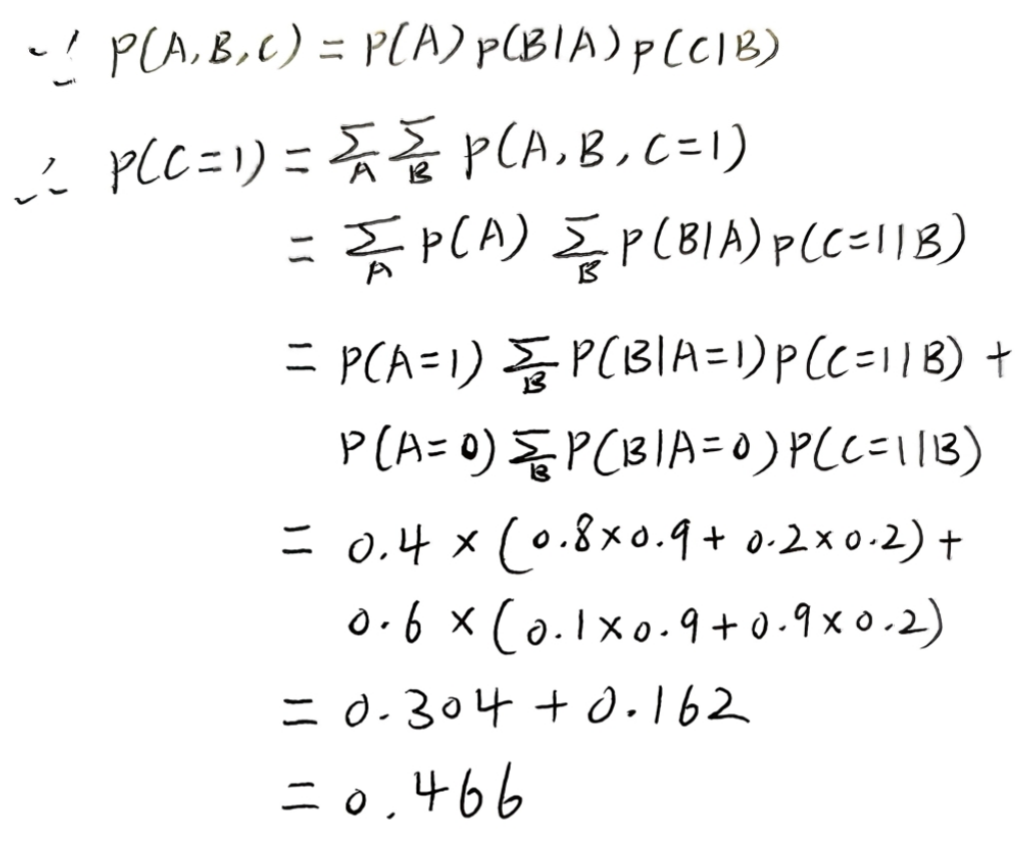[机器学习-从入门到入土] 概率图模型

个人导航

知乎：https://www.zhihu.com/people/byzh_rc

CSDN：https://blog.csdn.net/qq_54636039

注：本文仅对所述内容做了框架性引导，具体细节可查询其余相关资料or源码

参考文章：各方资料

文章目录

[[机器学习-从入门到入土] 概率图模型](#[机器学习-从入门到入土] 概率图模型)
个人导航
概率图模型 (Probabilistic Graphical Models)
贝叶斯网络 (Bayesian networks)
- - - 联合分布
[条件独立（Conditional Independence）](#条件独立（Conditional Independence）)
- - - [1. 结构类型](#1. 结构类型)
    - [2. D划分](#2. D划分)
马尔可夫随机场 (Markov Random Fields)
[图模型的推断 Inference in Graphical Models](#图模型的推断 Inference in Graphical Models)
例题

概率图模型 (Probabilistic Graphical Models)

可视化概率模型的工具，用 "图" 的形式把概率关系直观呈现出来

节点：代表随机变量（或一组随机变量）
边：代表变量之间的概率关系

概率图模型主要分两类：

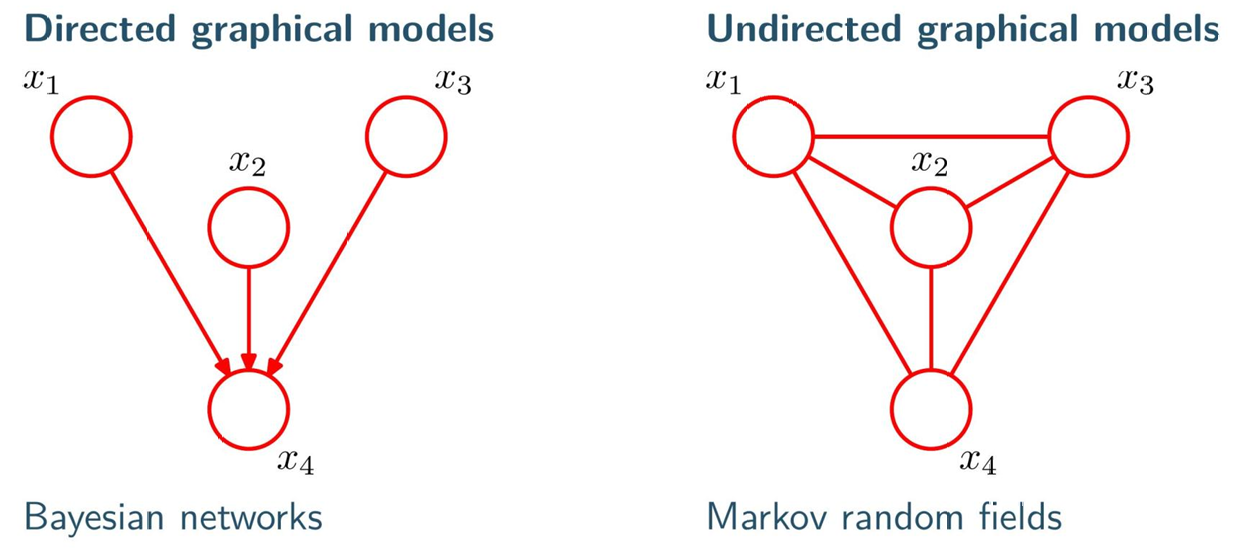
有向图模型（Directed graphical models）
- 图中的边是带方向的箭头，对应 "贝叶斯网络（Bayesian networks）"
- 箭头通常表示 "因果 / 依赖关系"
无向图模型（Undirected graphical models）
- 图中的边是无方向的连线，对应 "马尔可夫随机场（Markov random fields）"
- 连线表示变量之间的 "关联关系"

贝叶斯网络 (Bayesian networks)

贝叶斯网络的本质是用 "有向图" 表示变量的条件概率依赖关系

其数学基础是 "概率乘积公式"：
p ( A B ) = p ( A ∣ B ) p ( B ) p(AB) = p(A| B) p(B) p(AB)=p(A∣B)p(B)

两个事件的联合概率，等于其中一个事件在另一事件条件下的概率，乘以另一事件的概率

联合分布

以变量 a 、 b 、 c a、b、c a、b、c为例，推导它们的联合分布 p ( a , b , c ) p(a,b,c) p(a,b,c)：

第一次用乘积公式：把 a , b a,b a,b 看作整体， c c c 是条件变量

p ( a , b , c ) = p ( c ∣ a , b ) ⋅ p ( a , b ) p(a,b,c) = p(c|a,b) \cdot p(a,b) p(a,b,c)=p(c∣a,b)⋅p(a,b)
第二次用乘积公式：拆分 p ( a , b ) p(a,b) p(a,b)

p ( a , b , c ) = p ( c ∣ a , b ) ⋅ p ( b ∣ a ) ⋅ p ( a ) p(a,b,c) = p(c|a,b) \cdot p(b|a) \cdot p(a) p(a,b,c)=p(c∣a,b)⋅p(b∣a)⋅p(a)

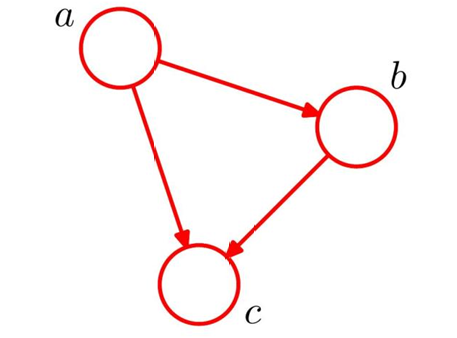
节点代表变量 a 、 b 、 c a、b、c a、b、c

箭头表示 "条件依赖"：

a指向b → b依赖a（对应 p ( b ∣ a ) p(b|a) p(b∣a)
a指向c、b指向c → c依赖a和b（对应 p ( c ∣ a , b ) p(c|a,b) p(c∣a,b)）

扩展到 K 个变量的通用形式:

对于K个变量 x 1 , x 2 , . . . , x K x_1,x_2,...,x_K x1,x2,...,xK，重复用乘积公式，联合分布可写成：
p ( x 1 , . . . , x K ) = p ( x K ∣ x 1 , . . . , x K − 1 ) ⋅ . . . ⋅ p ( x 2 ∣ x 1 ) ⋅ p ( x 1 ) p(x_1,...,x_K) = p(x_K|x_1,...,x_{K-1}) \cdot ... \cdot p(x_2|x_1) \cdot p(x_1) p(x1,...,xK)=p(xK∣x1,...,xK−1)⋅...⋅p(x2∣x1)⋅p(x1)

此时对应的图是 "全连接的"（每对节点都有依赖关系）

贝叶斯网络里，没有边 = 变量之间无直接概率依赖

没有边的变量，不会出现在对方的条件概率里

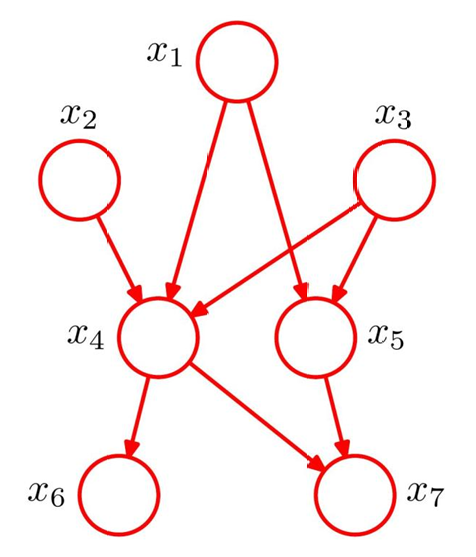
x 1 x_1 x1到 x 2 x_2 x2没有边、 x 3 x_3 x3到 x 7 x_7 x7没有边 → 说明 x 2 x_2 x2不直接依赖 x 1 x_1 x1， x 7 x_7 x7不直接依赖 x 3 x_3 x3

因此联合分布可以 "简化" 为：
p ( x 1 ) p ( x 2 ) p ( x 3 ) p ( x 4 ∣ x 1 , x 2 , x 3 ) p ( x 5 ∣ x 1 , x 3 ) p ( x 6 ∣ x 4 ) p ( x 7 ∣ x 4 , x 5 ) p(x_1)p(x_2)p(x_3)p(x_4|x_1,x_2,x_3)p(x_5|x_1,x_3)p(x_6|x_4)p(x_7|x_4,x_5) p(x1)p(x2)p(x3)p(x4∣x1,x2,x3)p(x5∣x1,x3)p(x6∣x4)p(x7∣x4,x5)

在|前的是某个节点

在|后面的是其直接相关的父节点(不管祖父)

贝叶斯网络的有向图必须是无环图（DAG，Directed Acyclic Graphs） ：

不能出现 " x 1 → x 2 → x 3 → x 1 x_1→x_2→x_3→x_1 x1→x2→x3→x1" 这样的有向环，否则条件依赖关系会矛盾（无法定义合理的条件概率）

条件独立（Conditional Independence）

条件独立的定义:

当 "给定变量c时，a的概率分布不依赖b"，则称 **a和b在给定c的条件下独立 **, 记为 a ⊥ b ∣ c a \perp b \mid c a⊥b∣c

数学表达为 p ( a , b ∣ c ) = p ( a ∣ c ) ⋅ p ( b ∣ c ) p(a,b|c) = p(a|c) \cdot p(b|c) p(a,b∣c)=p(a∣c)⋅p(b∣c)

作用：简化模型（不用画 a − b a-b a−b的边）、降低计算量（分解复杂运算）

独立: a与b毫无瓜葛
不独立: a与b有相关

1. 结构类型

结构类型	未观测c时( ∅ \varnothing ∅)	观测c时( c c c)
尾到尾（ a ← c → b a \leftarrow c \rightarrow b a←c→b）	a 、 b a、b a、b不独立	a 、 b a、b a、b独立
头到尾（ a → c → b a \rightarrow c \rightarrow b a→c→b）	a 、 b a、b a、b不独立	a 、 b a、b a、b独立
头到头（ a → c ← b a \rightarrow c \leftarrow b a→c←b）	a 、 b a、b a、b独立	a 、 b a、b a、b不独立

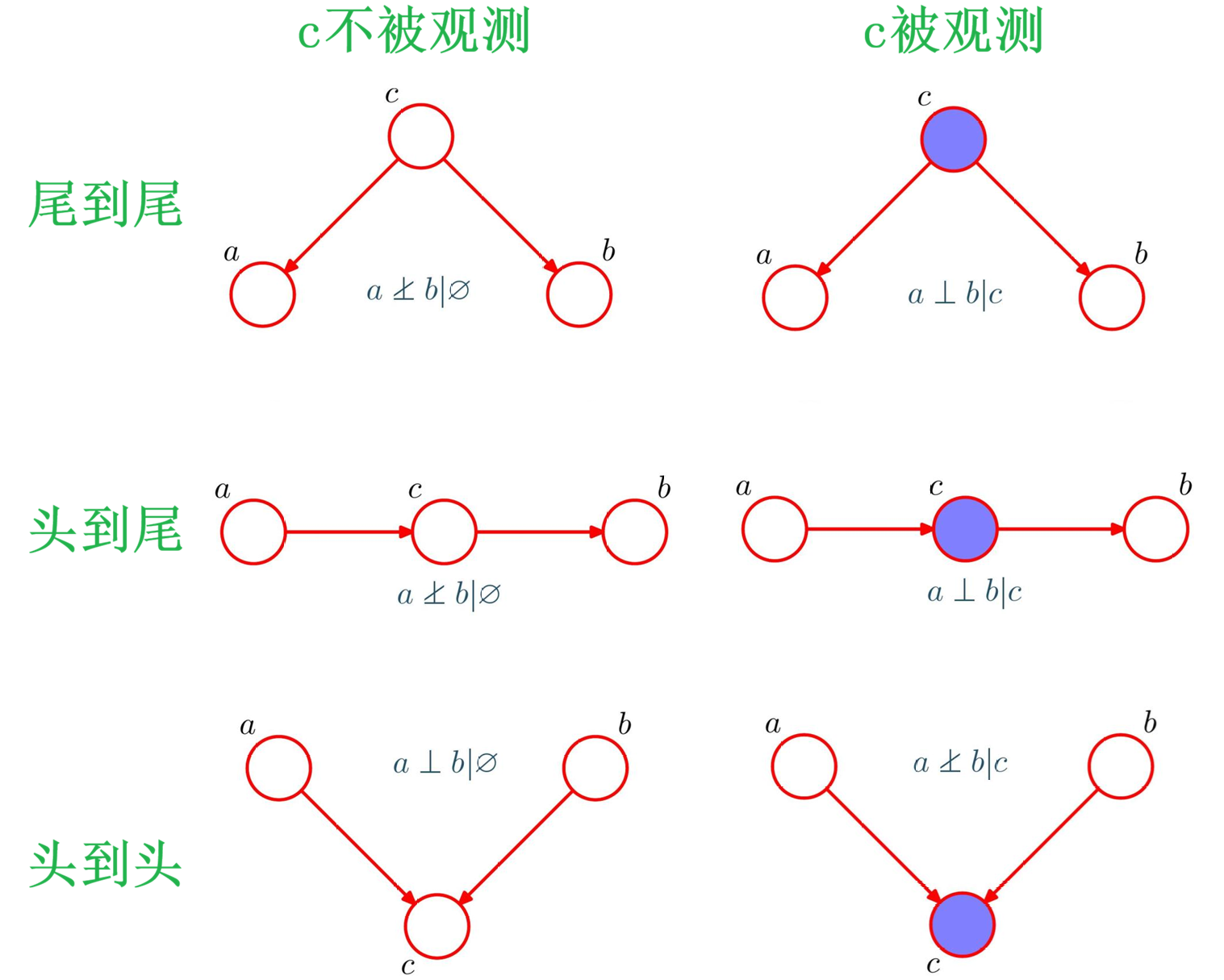
对于尾到尾和头到尾:

在不观测 c c c 时， a a a 和 b b b 通过**"对共同原因的不确定性"产生了统计相关** -> 不独立

而一旦观测了 c c c，这种相关性的唯一来源被"消除"，两者只剩下各自的随机性 -> 独立

对于头到头:

不观测 c c c 时两个原因互不传递信息 -> 独立

而一旦观测 c c c， a a a 与 b b b 就必须"共同解释"这个结果，彼此产生解释竞争，从而变得相关 -> 不独立

2. D划分

D 划分是判断 "集合A和B在给定集合C时是否独立/是否阻断" 的方法：

若A到B的所有路径都被阻断，则 A ⊥ B ∣ C A \perp B \mid C A⊥B∣C -> 阻断则独立
"阻断相关性路径" 的条件：
1. 路径中节点是头 - 尾 / 尾 - 尾 ，且该节点属于C（被观测）
2. 路径中节点是头 - 头 ，且该节点及其后代节点都不属于C（未观测）

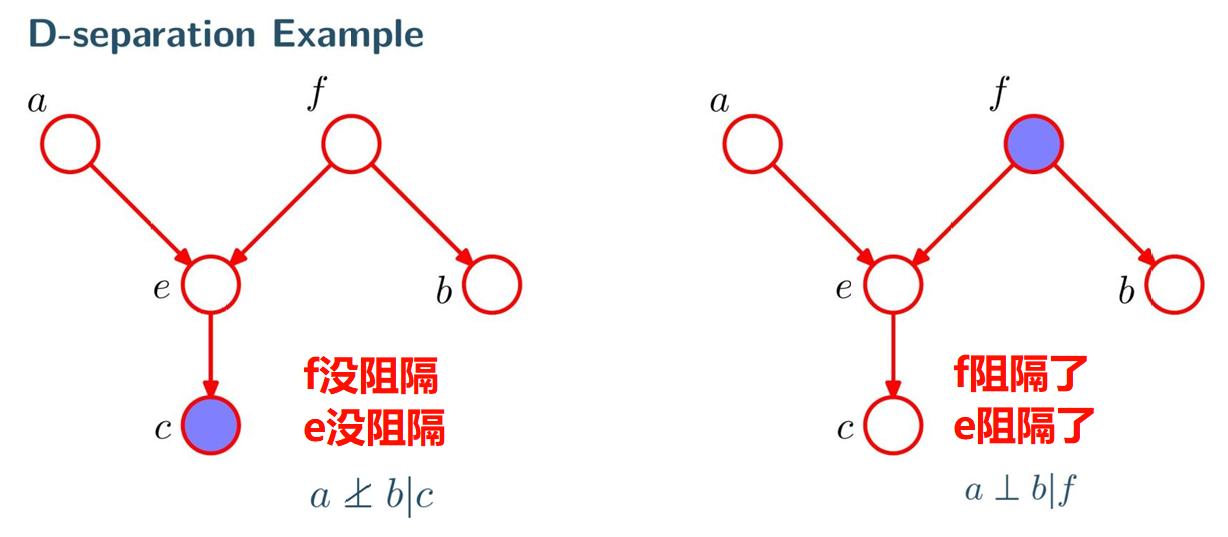
c被观测的情况下, 问a与b:

e是头到头, 后迭代被观测 -> 产生解释竞争 -> 不阻断

f是尾到尾, 未被观测 -> 有共因的不确定性 -> 不阻断

e的后代c被观测, 相当于e被观测

f被观测的情况下, 问a与b:

e是头到头, 未被观测 -> 互不相干 -> 阻断

f是尾到尾, 被观测 -> 无不确定性 -> 阻断

马尔可夫随机场 (Markov Random Fields)

马尔可夫随机场是无向概率图模型的核心代表

核心思想是利用图的拓扑结构 描述变量间的依赖与独立关系，并用势函数的乘积形式定义联合概率分布

无向图的条件独立性（马尔可夫性）

变量集合的条件独立性由 路径是否被 "阻断" 判断：

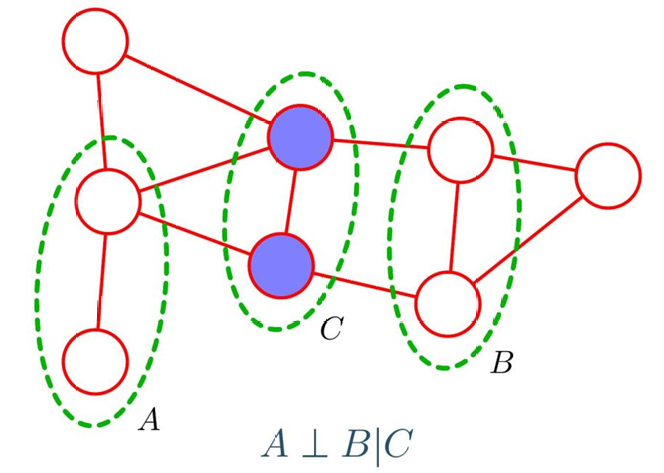
设变量集合分为 A , B , C A,B,C A,B,C 三部分。若连接 A 和 B 的所有路径 都必须经过 C 中的节点，则称 C 阻断了 A 和 B 之间的路径。此时条件独立性成立： A ⊥ B ∣ C A\perp B \mid C A⊥B∣C（即给定 C 时，A 和 B 相互独立）
若存在至少一条路径不经过 C，则 A 和 B 的条件独立性不成立

团块（Clique）与最大团块

团块是无向图中定义联合分布的基础单元

团块：节点的一个子集，满足子集中任意两个节点之间都有边连接（子集内节点两两相邻）
最大团块：无法再加入任何节点的团块（加入后不再满足团块的定义），即当前节点数最多的团块

无向图的联合概率分布

马尔可夫随机场的联合分布通过团块势函数 的乘积归一化得到，公式如下：
p ( x ) = 1 Z ∏ C ψ C ( x C ) p(\mathbf{x})=\frac{1}{Z}\prod_{C}\psi_{C}\left(\mathbf{x}_{C}\right) p(x)=Z1C∏ψC(xC)

其中各符号含义：

C C C：图中的所有团块
x C \mathbf{x}_C xC：团块 C 中所有节点对应的变量取值
ψ C ( x C ) \psi_C(\mathbf{x}_C) ψC(xC)：团块势函数 ，是定义在团块上的非负函数，用于刻画团块内变量间的依赖关系（势函数值越大，对应变量组合出现的概率越高）
Z：归一化常数 （也称为配分函数），作用是让联合分布的总和为 1，其计算公式为：
Z = ∑ x ∏ C ψ C ( x C ) Z=\sum_{\mathbf{x}}\prod_{C}\psi_{C}\left(\mathbf{x}_{C}\right) Z=x∑C∏ψC(xC)

注：Z 的计算需要对所有变量的可能取值组合求和，当变量维度较高时，Z 的计算会非常困难

有向图转无向图

1.链式有向图的转换:

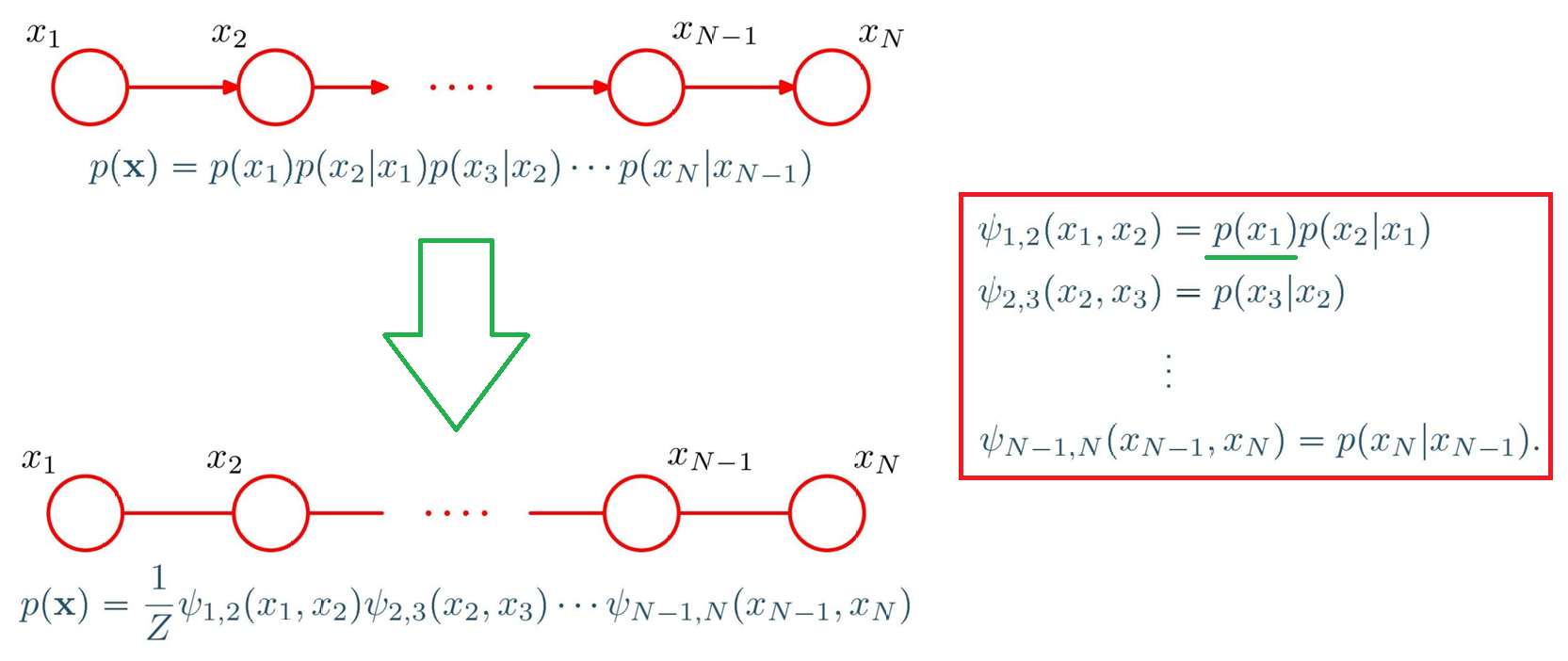
为了让无向图的分布和原有的向图分布一致，势函数要匹配原分布的项：

第一个团 { x 1 , x 2 } \{x_1,x_2\} {x1,x2}的势函数： ψ 1 , 2 ( x 1 , x 2 ) = p ( x 1 ) p ( x 2 ∣ x 1 ) \psi_{1,2}(x_1,x_2) = p(x_1)p(x_2|x_1) ψ1,2(x1,x2)=p(x1)p(x2∣x1)（对应原分布的前两项）

后面的团（比如 { x 2 , x 3 } \{x_2,x_3\} {x2,x3}）的势函数： ψ 2 , 3 ( x 2 , x 3 ) = p ( x 3 ∣ x 2 ) \psi_{2,3}(x_2,x_3) = p(x_3|x_2) ψ2,3(x2,x3)=p(x3∣x2)（对应原分布的条件概率项）

2.带多父节点的有向图转换（道德化moralization）:

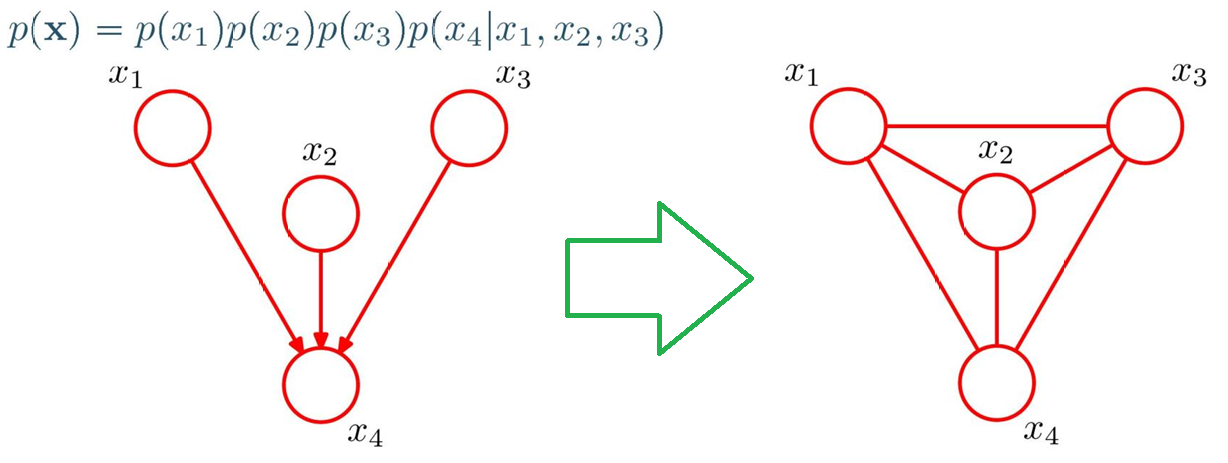
"涉及多个变量的因子（比如 p ( x 4 ∣ x 1 , x 2 , x 3 ) p(x_4|x_1,x_2,x_3) p(x4∣x1,x2,x3)）" 必须对应一个团（团要求变量两两相连）

道德化操作 ：在 x 4 x_4 x4的所有父节点（ x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3）之间两两添加无向边 （相当于 "把父节点们连起来"），这样 x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1,x2,x3,x4就构成了一个团（所有变量两两相连）

"连接父节点" 的过程就是道德化 ，得到的无向图叫道德图

道德化的目的是让 "原分布中涉及多个变量的条件概率项"，能对应无向图中的一个团，从而用势函数表示

图模型的推断 Inference in Graphical Models

在已知一部分变量（观测）的情况下，通过图结构高效地计算"另一些变量的概率分布"

1.贝叶斯定理的图表示（二元变量场景）

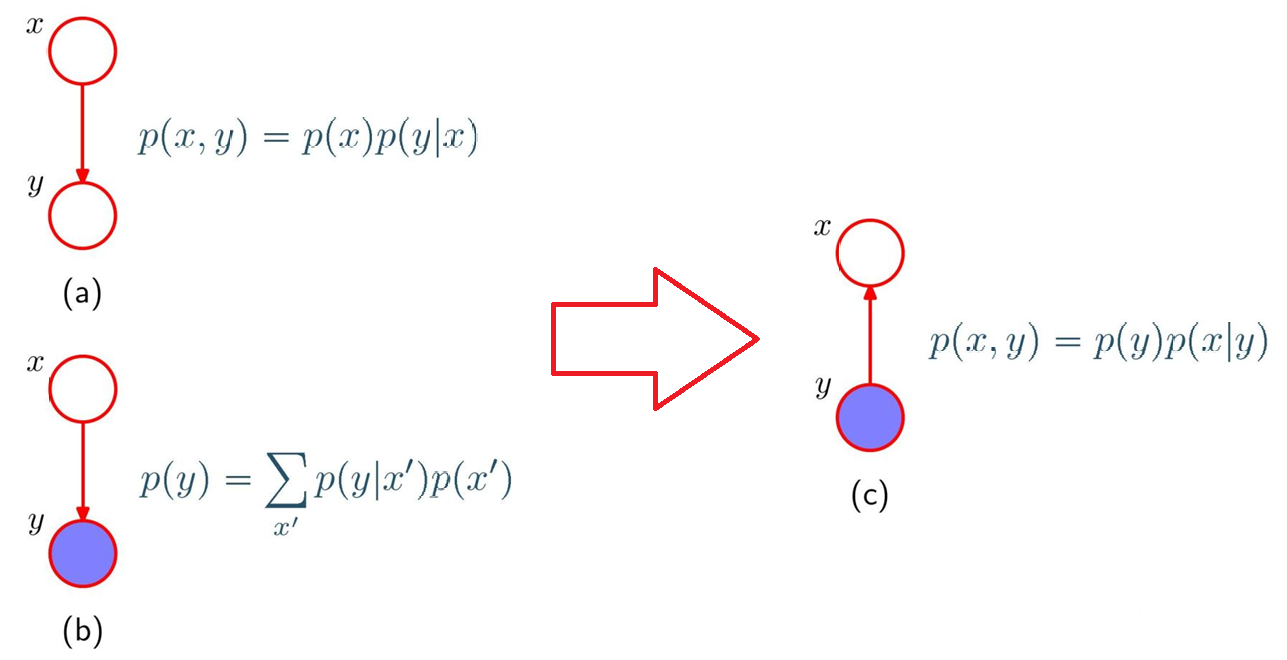
二元变量的联合分布可分解为 "先验 × 条件概率"： p ( x , y ) = p ( x ) p ( y ∣ x ) p(x,y) = p(x)p(y|x) p(x,y)=p(x)p(y∣x)

对应图（a）：x 到 y 的有向边表示依赖关系

观测到 y 后，用 "和积规则" 计算 y 的边缘分布： p ( y ) = ∑ x ′ p ( y ∣ x ′ ) p ( x ′ ) p(y) = \sum_{x'} p(y|x')p(x') p(y)=∑x′p(y∣x′)p(x′)

对应图（b）：y 被观测（蓝色）

由联合分布的分解形式（ p ( x , y ) = p ( y ) p ( x ∣ y ) p(x,y)=p(y)p(x|y) p(x,y)=p(y)p(x∣y)），推导后验概率： p ( x ∣ y ) = p ( y ∣ x ) p ( x ) p ( y ) p(x|y) = \frac{p(y|x)p(x)}{p(y)} p(x∣y)=p(y)p(y∣x)p(x)

对应图（c）：信息从观测变量 y 反向传递到 x

2.马尔可夫链的联合分布

若变量 x 1 , x 2 , ... , x N x_1,x_2,\dots,x_N x1,x2,...,xN 构成马尔可夫链 （仅相邻变量有依赖，图为链式结构），其联合分布可表示为：
p ( x ) = 1 Z ψ 1 , 2 ( x 1 , x 2 ) ψ 2 , 3 ( x 2 , x 3 ) ⋯ ψ N − 1 , N ( x N − 1 , x N ) p(\mathbf{x}) = \frac{1}{Z}\psi_{1,2}(x_1,x_2)\psi_{2,3}(x_2,x_3)\cdots\psi_{N-1,N}(x_{N-1},x_N) p(x)=Z1ψ1,2(x1,x2)ψ2,3(x2,x3)⋯ψN−1,N(xN−1,xN)

其中：

ψ i , i + 1 ( x i , x i + 1 ) \psi_{i,i+1}(x_i,x_{i+1}) ψi,i+1(xi,xi+1)：相邻变量的 "势函数"（刻画依赖关系）
Z：归一化常数（保证分布和为 1）

3.马尔可夫链的边缘分布推断（信息传递法）

要计算某节点 x n x_n xn 的边缘分布 p ( x n ) p(x_n) p(xn)，需通过 信息传递（Message Passing） 实现：

边缘分布的定义 ：

对联合分布求和（积分）掉除 x n x_n xn 外的所有变量： p ( x n ) = ∑ x 1 ⋯ ∑ x n − 1 ∑ x n + 1 ⋯ ∑ x N p ( x ) p(x_n) = \sum_{x_1}\cdots\sum_{x_{n-1}}\sum_{x_{n+1}}\cdots\sum_{x_N} p(\mathbf{x}) p(xn)=∑x1⋯∑xn−1∑xn+1⋯∑xNp(x)
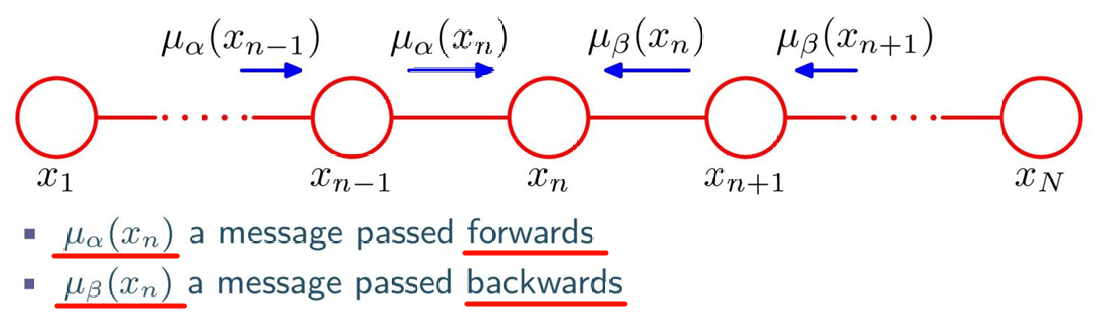
信息的拆分与传递 ：

边缘分布可拆分为 "从左到右的前向信息" 和 "从右到左的后向信息" 的乘积：
p ( x n ) = 1 Z μ α ( x n ) μ β ( x n ) p(x_n) = \frac{1}{Z}\mu_\alpha(x_n)\mu_\beta(x_n) p(xn)=Z1μα(xn)μβ(xn)
- μ α ( x n ) \mu_\alpha(x_n) μα(xn)：前向信息 （从 x 1 x_1 x1 传递到 x n x_n xn 的累积依赖）
- μ β ( x n ) \mu_\beta(x_n) μβ(xn)：后向信息 （从 x N x_N xN 传递到 x n x_n xn 的累积依赖）
信息的递归计算 ：

信息可通过相邻节点递归更新（对应Chapman-Kolmogorov 方程）：
- 前向信息： μ α ( x n ) = ∑ x n − 1 ψ n − 1 , n ( x n − 1 , x n ) μ α ( x n − 1 ) \mu_\alpha(x_n) = \sum_{x_{n-1}} \psi_{n-1,n}(x_{n-1},x_n)\mu_\alpha(x_{n-1}) μα(xn)=∑xn−1ψn−1,n(xn−1,xn)μα(xn−1)（从左向右传递）
- 后向信息： μ β ( x n ) = ∑ x n + 1 ψ n + 1 , n ( x n + 1 , x n ) μ β ( x n + 1 ) \mu_\beta(x_n) = \sum_{x_{n+1}} \psi_{n+1,n}(x_{n+1},x_n)\mu_\beta(x_{n+1}) μβ(xn)=∑xn+1ψn+1,n(xn+1,xn)μβ(xn+1)（从右向左传递）

[机器学习-从入门到入土] 概率图模型