[机器学习-从入门到入土] 生成式模型

个人导航

知乎：https://www.zhihu.com/people/byzh_rc

CSDN：https://blog.csdn.net/qq_54636039

注：本文仅对所述内容做了框架性引导，具体细节可查询其余相关资料or源码

参考文章：各方资料

文章目录

[[机器学习-从入门到入土] 生成式模型](#[机器学习-从入门到入土] 生成式模型)
个人导航
[生成式模型 generative model](#生成式模型 generative model)
概率PCA(PPCA)
- - - 1.模型定义
    - [2.生成过程（2维数据空间 + 1维隐空间）](#2.生成过程（2维数据空间 + 1维隐空间）)
    - 3.极大似然参数估计
    - 4.矩阵求逆与后验分布
[自回归模型 AR](#自回归模型 AR)
- - - 1.核心原理
    - 2.架构
[变分自动编码器 VAE](#变分自动编码器 VAE)
[生成对抗网络 GAN](#生成对抗网络 GAN)
[扩散模型 diffusion model](#扩散模型 diffusion model)
总结

生成式模型 generative model

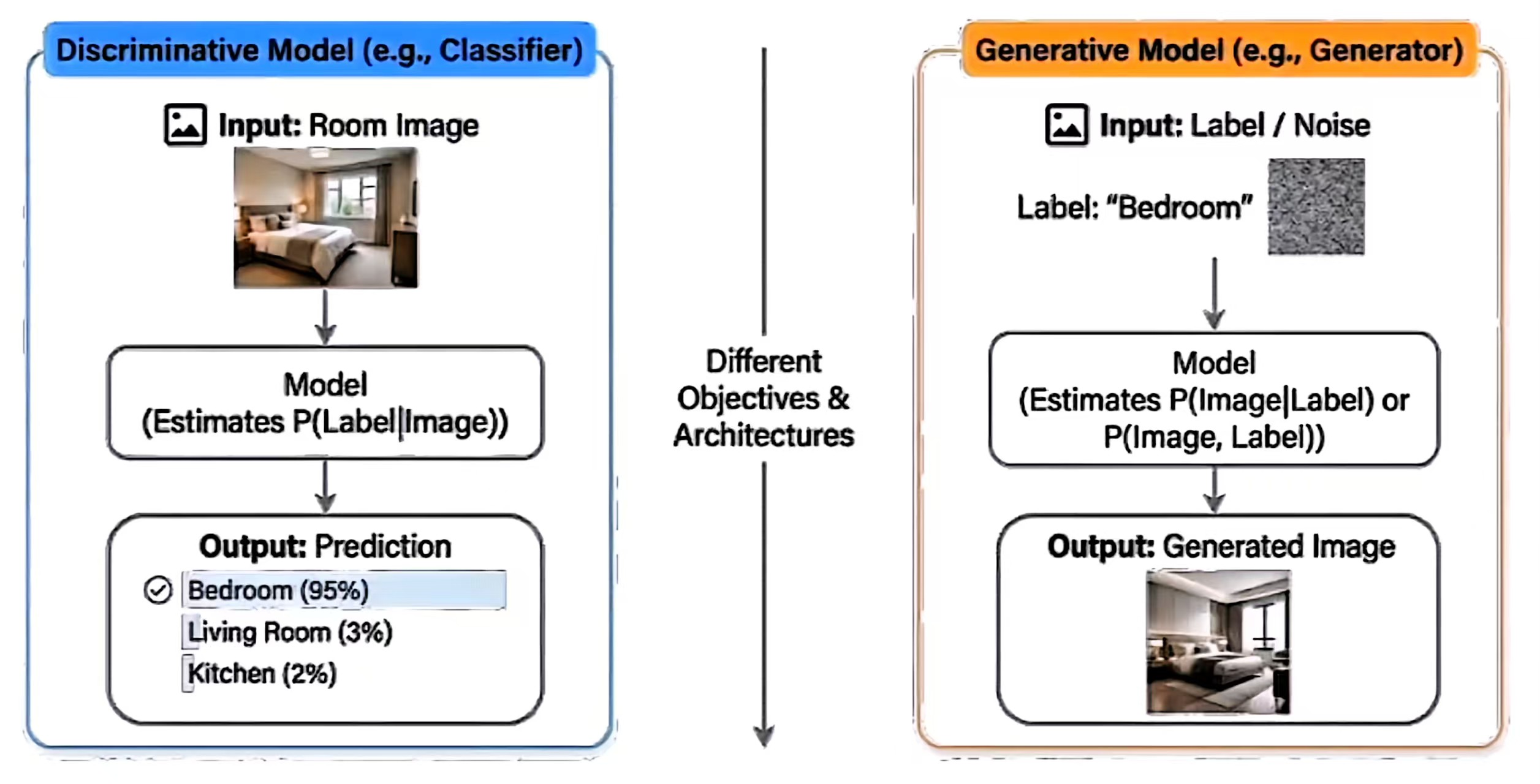
以往: 判别式模型discriminative model

学习后验概率 P ( Y ∣ X ) P(Y|X) P(Y∣X)
核心目标：找到不同类别之间的决策边界
示例：将一张图片分类为 "猫" 或 "狗"

当前介绍: 生成式模型generative model

学习联合概率 P ( X , Y ) P(X,Y) P(X,Y) 或数据分布 P ( X ) P(X) P(X)

联合概率 P ( X , Y ) P(X,Y) P(X,Y): 数据和标签是如何一起出现的

数据分布 P ( X ) P(X) P(X): 数据本身是如何分布的
核心目标：理解数据是如何生成的
核心洞见：如果你能生成数据，就意味着你理解了它的结构

需要生成式模型的原因：

采样 / 内容合成：生成逼真的图像、音频、文本
密度估计 / 异常检测：评估某个样本的出现概率
补全与逆问题：填补缺失数据、解决逆任务
半监督 / 自监督学习：利用 P ( X ) P(X) P(X) 来利用无标签数据

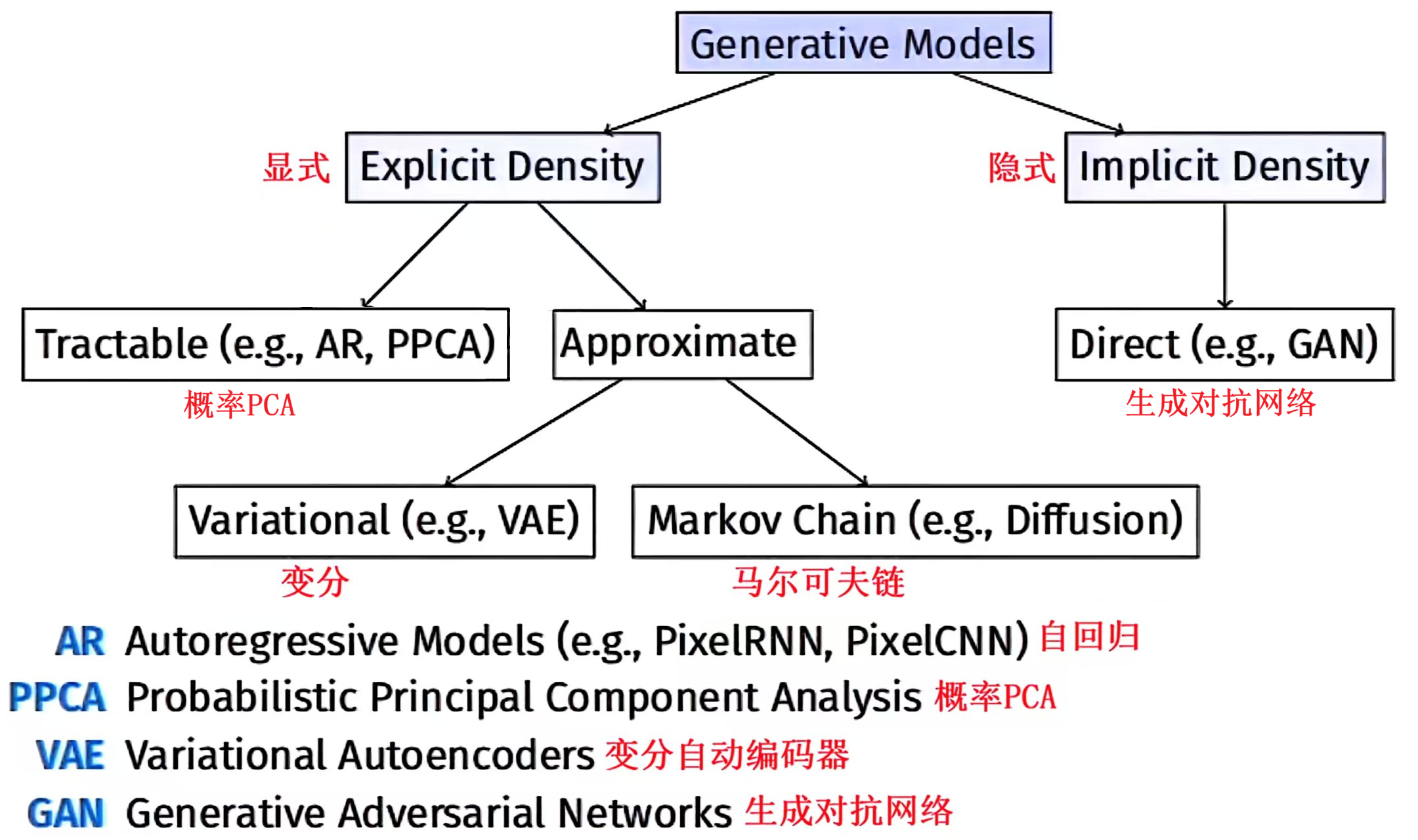
概率PCA(PPCA)

学习了数据的概率分布 p ( x ) p(\boldsymbol{x}) p(x)

1.模型定义

首先，引入显式隐变量 $\\boldsymbol{z}$ ，对应主成分子空间
为隐变量定义高斯先验分布 p ( z ) p(\boldsymbol{z}) p(z)：
p ( z ) = N ( z ∣ 0 , I ) p(\boldsymbol{z}) = \mathcal{N}(\boldsymbol{z} \mid \boldsymbol{0}, \boldsymbol{I}) p(z)=N(z∣0,I)
为观测变量 $\\boldsymbol{x}$ 定义基于隐变量的高斯条件分布 p ( x ∣ z ) p(\boldsymbol{x} \mid \boldsymbol{z}) p(x∣z)：
p ( x ∣ z ) = N ( x ∣ W z + μ , σ 2 I ) p(\boldsymbol{x} \mid \boldsymbol{z}) = \mathcal{N}(\boldsymbol{x} \mid \boldsymbol{Wz} + \boldsymbol{\mu}, \sigma^2 \boldsymbol{I}) p(x∣z)=N(x∣Wz+μ,σ2I)
生成视角理解：
x = W z + μ + ϵ \boldsymbol{x} = \boldsymbol{Wz} + \boldsymbol{\mu} + \boldsymbol{\epsilon} x=Wz+μ+ϵ

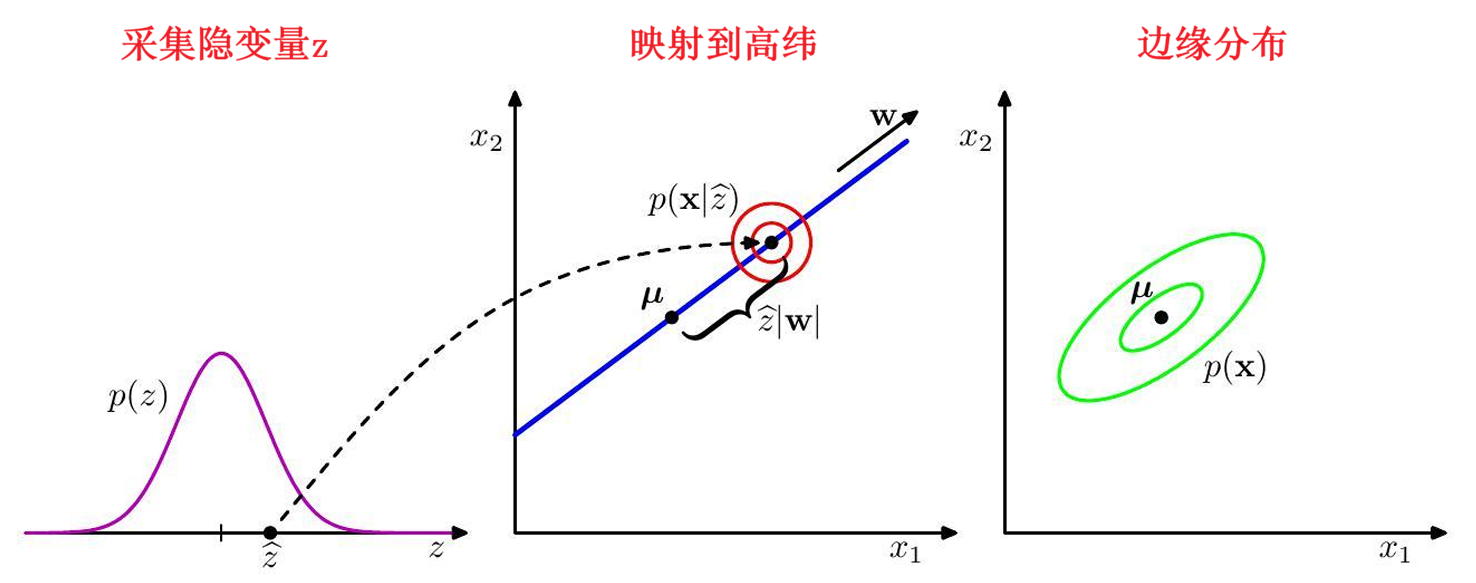
2.生成过程（2维数据空间 + 1维隐空间）

概率主成分分析的生成逻辑：

从隐变量先验分布 p ( z ^ ) p(\hat{\boldsymbol{z}}) p(z^) 抽取隐变量取值 z ^ \hat{\boldsymbol{z}} z^
从各向同性的高斯分布 （红色圆圈示意）中抽取观测数据点 x \boldsymbol{x} x，该分布的：
- 均值： w z ^ + μ \boldsymbol{w}\hat{\boldsymbol{z}} + \boldsymbol{\mu} wz^+μ
- 协方差： σ 2 I \sigma^2 \boldsymbol{I} σ2I

绿色椭圆代表边缘分布 p ( x ) p(\boldsymbol{x}) p(x) 的密度等高线

3.极大似然参数估计

通过极大似然法确定参数 W 、 μ 、 σ 2 \boldsymbol{W}、\boldsymbol{\mu}、\sigma^2 W、μ、σ2，需先得到边缘分布 p ( x ) p(\boldsymbol{x}) p(x)：
p ( x ) = ∫ p ( x ∣ z ) p ( z ) d z = N ( x ∣ μ , C ) p(\boldsymbol{x}) = \int p(\boldsymbol{x} \mid \boldsymbol{z}) p(\boldsymbol{z}) d\boldsymbol{z} = \mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{C}) p(x)=∫p(x∣z)p(z)dz=N(x∣μ,C)

其中 d × d d \times d d×d 维协方差矩阵 C \boldsymbol{C} C 定义为：
C = W W T + σ 2 I \boldsymbol{C} = \boldsymbol{WW}^T + \sigma^2 \boldsymbol{I} C=WWT+σ2I

4.矩阵求逆与后验分布

计算预测分布时需用到 C − 1 \boldsymbol{C}^{-1} C−1，利用矩阵求逆恒等式 可得：
C − 1 = σ − 2 I − σ − 2 W M − 1 W T \boldsymbol{C}^{-1} = \sigma^{-2}\boldsymbol{I} - \sigma^{-2}\boldsymbol{WM}^{-1}\boldsymbol{W}^T C−1=σ−2I−σ−2WM−1WT

其中 d ′ × d ′ d' \times d' d′×d′ 维矩阵 M \boldsymbol{M} M 定义为：
M = W T W + σ 2 I \boldsymbol{M} = \boldsymbol{W}^T\boldsymbol{W} + \sigma^2\boldsymbol{I} M=WTW+σ2I

后验分布 p ( z ∣ x ) p(\boldsymbol{z} \mid \boldsymbol{x}) p(z∣x) 的表达式为：
p ( z ∣ x ) = N ( z ∣ M − 1 W T ( x − μ ) , σ − 2 M ) p(\boldsymbol{z} \mid \boldsymbol{x}) = \mathcal{N}\left(\boldsymbol{z} \mid \boldsymbol{M}^{-1}\boldsymbol{W}^T(\boldsymbol{x} - \boldsymbol{\mu}), \sigma^{-2}\boldsymbol{M}\right) p(z∣x)=N(z∣M−1WT(x−μ),σ−2M)

自回归模型 AR

学习了数据的概率分布 p ( x ) p(\boldsymbol{x}) p(x)

AR: Auto-Regressive

regressive：用已知变量预测未知变量
auto：预测变量来自"自身序列"

自回归模型不是一种具体网络，而是一种"联合分布建模方式"：用过去变量去预测下一个变量

1.核心原理

利用概率链式法则分解联合分布：

p ( x ) = ∏ i = 1 n p ( x i ∣ x 1 , ... , x i − 1 ) p(x) = \prod_{i=1}^{n} p(x_i|x_1,\dots,x_{i-1}) p(x)=i=1∏np(xi∣x1,...,xi−1)

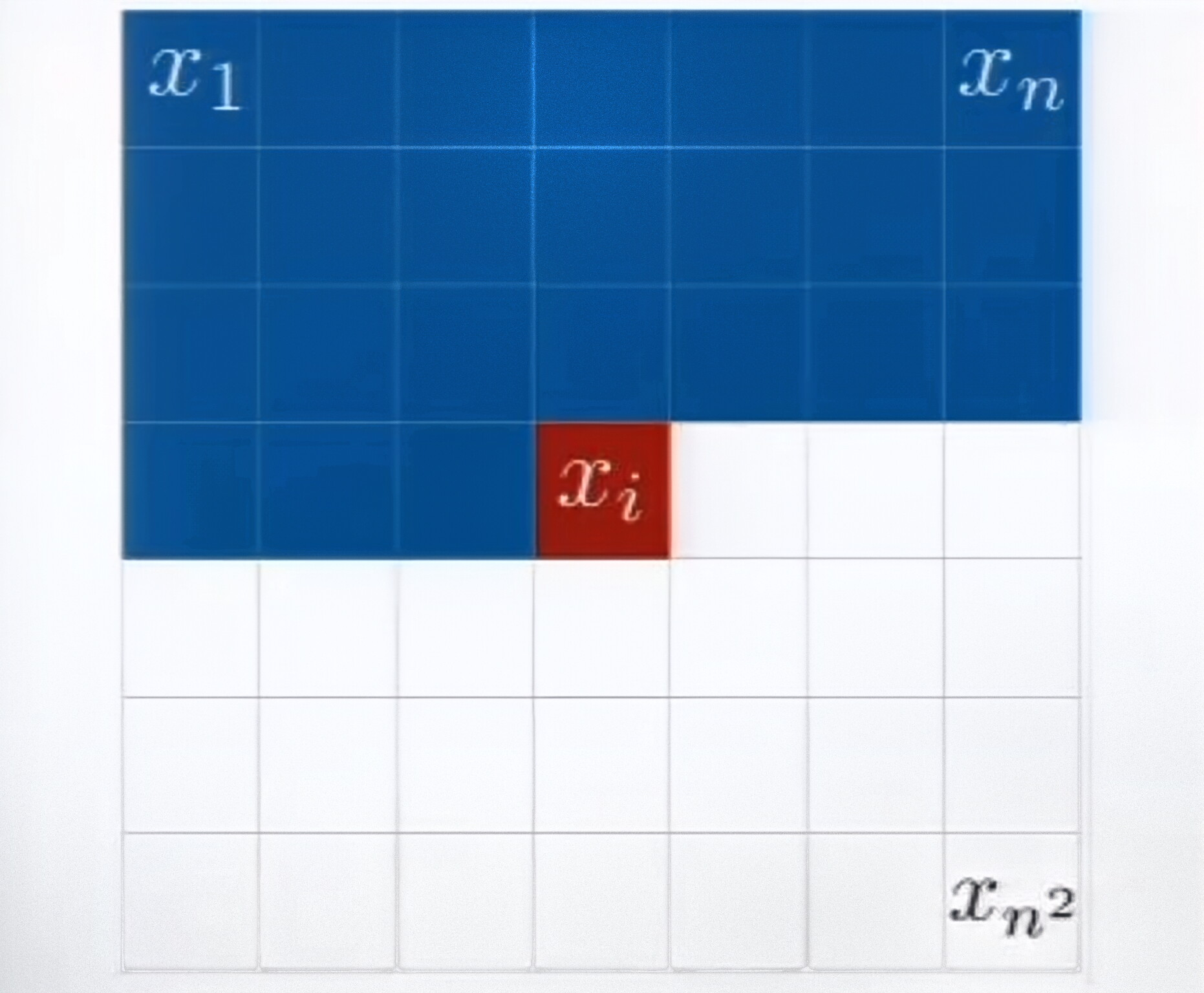
2.架构

因果性约束: 第 i i i 个输出只能依赖 x 1 , ... , x i − 1 x_1,\dots,x_{i-1} x1,...,xi−1，不能看到未来

循环神经网络（RNN）：适用于序列数据（文本、音频）
PixelRNN / PixelCNN：用于图像生成（逐像素生成）

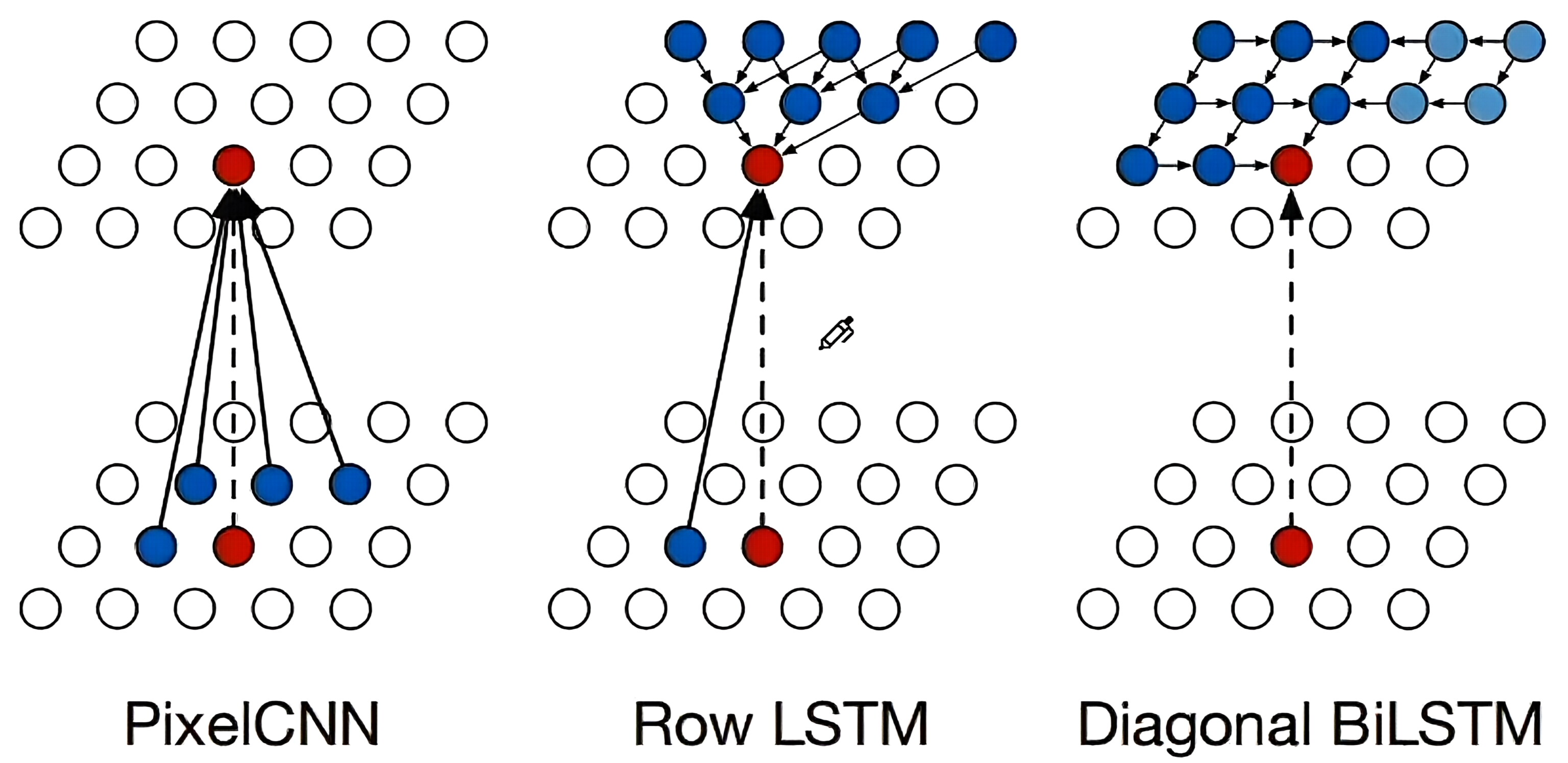
优点：可进行精确的似然计算（易于处理），训练难度低

缺点：序列生成的计算速度较慢

变分自动编码器 VAE

学习了数据的概率分布 p ( x ) p(\boldsymbol{x}) p(x)

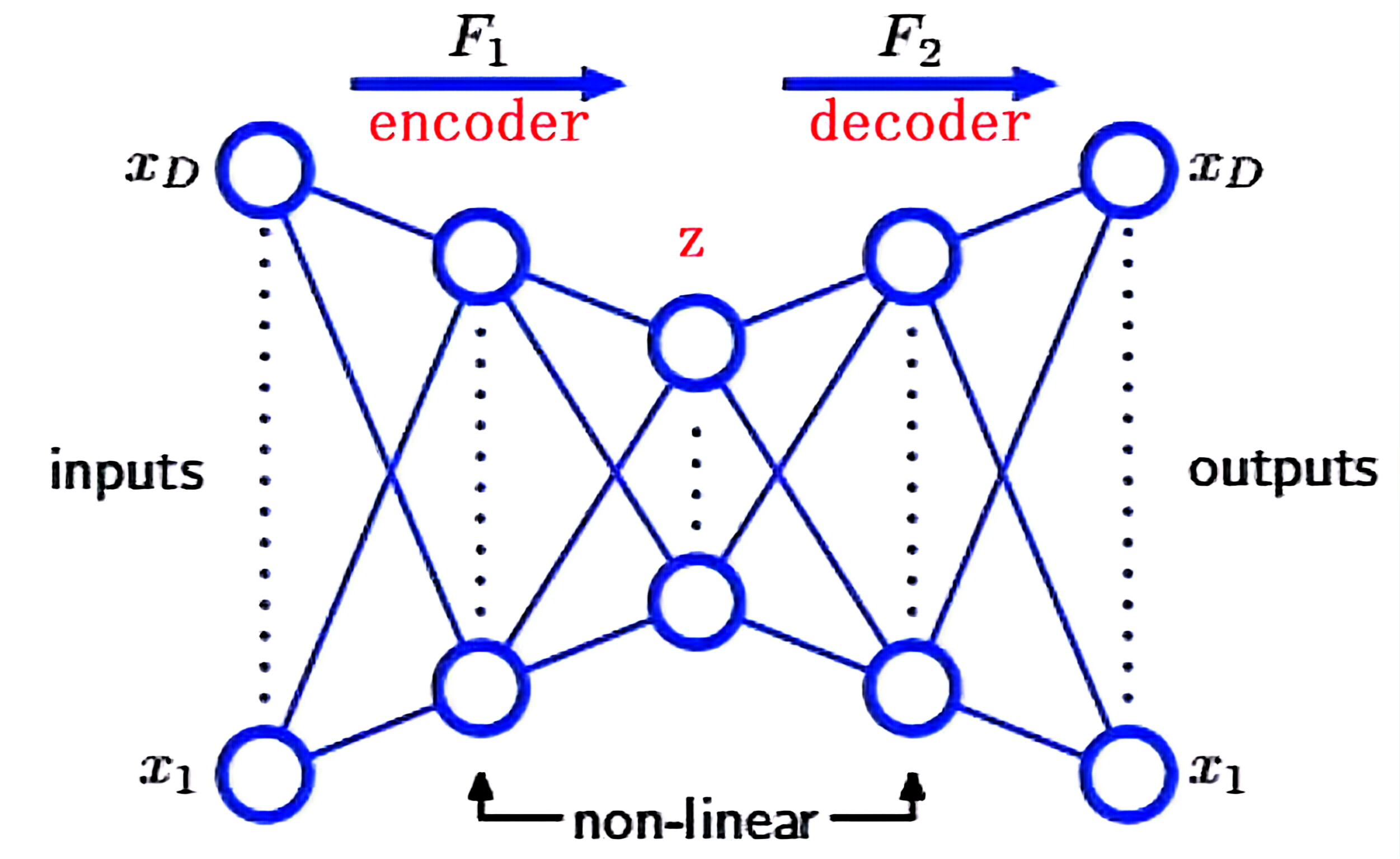
增加额外的非线性单元隐藏层，可得到能执行非线性降维的自联想网络

引入潜在变量z，用于捕捉变化因子（如姿态、光线等）
编码器 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x)：将输入映射到潜在空间
解码器 p θ ( x ∣ z ) p_\theta(x|z) pθ(x∣z)：从潜在变量中重构输入

目标：证据下界（ELBO）
log ⁡ p ( x ) ≥ E q ϕ ( z ∣ x ) [ log ⁡ p θ ( x ∣ z ) ] ⏟ 重构损失 − D KL ( q ϕ ( z ∣ x ) ∥ p ( z ) ) ⏟ 正则化项 \log p(x) \geq \underbrace{\mathbb{E}{q\phi(z|x)} \left[ \log p_\theta(x|z) \right]}{\text{重构损失}} - \underbrace{D{\text{KL}} \left( q_\phi(z|x) \parallel p(z) \right)}_{\text{正则化项}} logp(x)≥重构损失 Eqϕ(z∣x)[logpθ(x∣z)]−正则化项 DKL(qϕ(z∣x)∥p(z))

生成对抗网络 GAN

学习了数据的概率分布 p ( x ) p(\boldsymbol{x}) p(x)

GAN: generative adversarial network

两个神经网络相互对抗：

生成器（G）	判别器（D）
尝试生成逼真的假数据，以此欺骗判别器（输入z → 输出 G ( z ) G(z) G(z)）	尝试区分真实数据 x x x和假数据 G ( z ) G(z) G(z)

让生成器的分布 p g p_g pg 在对抗过程中逼近真实数据分布 p data p_{\text{data}} pdata

生成器与判别器通过如下价值函数 V ( G , D ) V(G,D) V(G,D) 进行极小极大博弈：
min ⁡ G max ⁡ D V ( G , D ) = E x ∼ p data [ log ⁡ D ( x ) ] + E z ∼ p z [ log ⁡ ( 1 − D ( G ( z ) ) ) ] \min_{G} \max_{D} V(G,D) = \mathbb{E}{x \sim p{\text{data}}} \left[ \log D(x) \right] + \mathbb{E}{z \sim p{z}} \left[ \log(1-D(G(z))) \right] GminDmaxV(G,D)=Ex∼pdata[logD(x)]+Ez∼pz[log(1−D(G(z)))]

优势：能生成非常清晰、高质量的图像
劣势：训练不稳定（难以找到纳什均衡）；存在模式崩溃问题；没有显式的似然密度

扩散模型 diffusion model

学习了数据的概率分布 p ( x ) p(\boldsymbol{x}) p(x)

扩散模型通过一个固定的"加噪马尔可夫过程"把真实数据逐步推向已知噪声分布，再学习其逆过程（逐步去噪），从而实现从噪声到数据的生成

正向过程（固定的） ：逐步向数据中添加高斯噪声，直到数据变成纯噪声（ x T x_T xT）
x 0 ⟶ 噪声 x 1 ... ⟶ 噪声 x T x_0 \stackrel{\text{噪声}}{\longrightarrow} x_1 \dots \stackrel{\text{噪声}}{\longrightarrow} x_T x0⟶噪声x1...⟶噪声xT

反向过程（可学习的） ：训练一个神经网络，对图像进行逐序去噪
x T ⟶ 去噪 x T − 1 ... ⟶ 去噪 x 0 x_T \stackrel{\text{去噪}}{\longrightarrow} x_{T-1} \dots \stackrel{\text{去噪}}{\longrightarrow} x_0 xT⟶去噪xT−1...⟶去噪x0

优势：与GAN相比，样本质量更高，训练更稳定

可用于:

局部缺失
遮挡修复
老照片修复

总结

模型	类型	优势	劣势
自回归模型AR	显式（易处理）	精确似然	采样速度慢
变分自动编码器VAE	显式（近似）	采样快、潜空间平滑	样本模糊
生成对抗网络GAN	隐式	样本清晰	训练不稳定
扩散模型diffusion	显式（近似）	质量高、训练稳定	采样慢（迭代式）