一、MLA 技术核心目标与设计本质
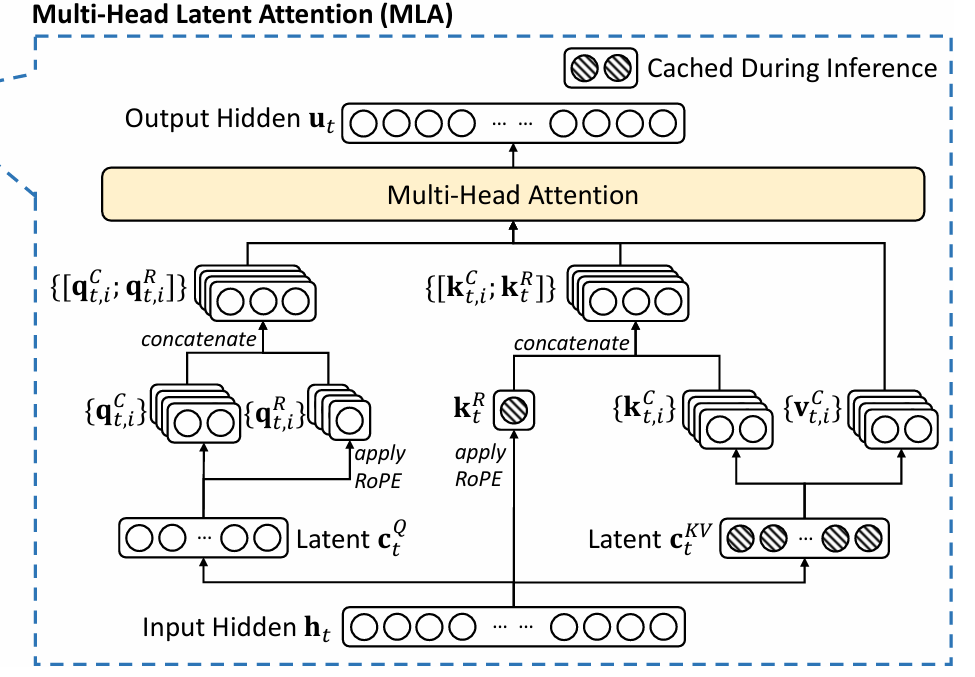
MLA(Multi-Head Latent Attention,多头潜在注意力)是 DeepSeek 提出的针对传统 MHA、MQA/GQA 的革新性注意力机制,核心目标是在保证模型性能的前提下,极大压缩 KV Cache 的内存占用(DeepSeek-V3 中每 token 仅需 70KB,是传统方法的 1/7 到 1/4),突破大模型推理时的显存瓶颈。
二、RoPE 核心数学特性(理解 MLA 设计的基础)
RoPE 是实现位置感知的关键技术,其数学特性直接决定了 MLA 中 RoPE 与压缩逻辑的搭配方式,核心特性如下:
-
数学定义 :设向量为 xxx ,位置为 mmm ,RoPE 操作可表示为与正交矩阵 RmR_mRm 的乘法: RoPE(x,m)=RmxRoPE(x, m) = R_m xRoPE(x,m)=Rmx (正交矩阵特性:不改变向量内积、夹角和长度)。
-
核心价值:相对位置表达:在 Attention 点积计算中,RoPE 可将绝对位置转化为相对位置关系,即:
(Rmq)T(Rnk)=qTRmTRnk=qTRn−mk(R_m q)^T (R_n k) = q^T R_m^T R_n k = q^T R_{n-m} k(Rmq)T(Rnk)=qTRmTRnk=qTRn−mk
该式表明,Query(Q)与 Key(K)的点积结果仅取决于两者的相对距离 n−mn-mn−m ,与绝对位置无关,这是 RoPE 实现位置感知的核心原理。
- 关键约束 :RoPE 的相对位置特性仅在点积操作前一步紧挨着发生时有效,中间若穿插非正交的线性变换(如 MLA 中的压缩/还原矩阵),会破坏旋转矩阵 RRR 的结构,导致相对位置关系丢失。
三、KV 侧设计解析
MLA 在 KV 侧的核心设计是"单独分支预测 kRk_RkR ":先通过矩阵 WKW_KWK 对上层输出 HHH 变换,再计算 kR=RoPE(WK⋅H)k_R = RoPE(W_K \cdot H)kR=RoPE(WK⋅H) ;同时将 KV 主体压缩为低维潜向量 cKVc_{KV}cKV 缓存。
1. 为何不采用"先 RoPE 再压缩/还原"或"压缩后 RoPE 再还原"?
核心原因:这两种方案会破坏 RoPE 的相对位置特性,具体通过数学推导验证(设 WDW_DWD 为压缩矩阵, WUW_UWU 为还原矩阵,均非正交矩阵):
- 方案 A:先 RoPE 再压缩( cQ=WDQ⋅RoPE(Hm,m)c_Q = W_{DQ} \cdot RoPE(H_m, m)cQ=WDQ⋅RoPE(Hm,m) 、 cK=WDK⋅RoPE(Hn,n)c_K = W_{DK} \cdot RoPE(H_n, n)cK=WDK⋅RoPE(Hn,n) ):
点积计算时: Score=(WUQWDQRmHm)T(WUKWDKRnHn)Score = (W_{UQ} W_{DQ} R_m H_m)^T (W_{UK} W_{DK} R_n H_n)Score=(WUQWDQRmHm)T(WUKWDKRnHn)
展开后可得:
Score=HmTRmT(WDQTWUQTWUKWDK)⏟MRnHnScore = H_m^T R_m^T \underbrace{(W_{DQ}^T W_{UQ}^T W_{UK} W_{DK})}_{M} R_n H_nScore=HmTRmTM (WDQTWUQTWUKWDK)RnHn
不合理性分析:中间复合矩阵 MMM 的介入,导致 RmTMRnR_m^T M R_nRmTMRn 无法合并为表征相对位置的 Rn−mR_{n-m}Rn−m 。
- 方案 B:压缩后 RoPE 再还原( K=WUK⋅RoPE(WDKHn,n)K = W_{UK} \cdot RoPE(W_{DK} H_n, n)K=WUK⋅RoPE(WDKHn,n) 、 Q=WUQ⋅RoPE(WDQHm,m)Q = W_{UQ} \cdot RoPE(W_{DQ} H_m, m)Q=WUQ⋅RoPE(WDQHm,m) ):
点积计算时:
Score=(WUQRmWDQHm)T(WUKRnWDKHn)Score = (W_{UQ} R_m W_{DQ} H_m)^T (W_{UK} R_n W_{DK} H_n)Score=(WUQRmWDQHm)T(WUKRnWDKHn)
展开后可得:
Score=(WDQHm)TRmT(WUQTWUK)⏟M′Rn(WDKHn)Score = (W_{DQ} H_m)^T R_m^T \underbrace{(W_{UQ}^T W_{UK})}{M'} R_n (W{DK} H_n)Score=(WDQHm)TRmTM′ (WUQTWUK)Rn(WDKHn)
不合理性分析:中间还原投影矩阵乘积 M′=WUQTWUKM' = W_{UQ}^T W_{UK}M′=WUQTWUK 的介入,破坏了旋转矩阵的交换律。
2. 为何不对还原后的 K 采用 RoPE?
计算开销,解码阶段需反复执行RoPE 操作,计算开销(FLOPs)极大,导致推理延迟显著增加。
3. 为何不直接对上层输出 H 做 RoPE,而是先经 W_K 矩阵变换?
上层输出 HHH 包含丰富语义特征,直接对 HHH 做 RoPE 会丢失"筛选位置相关特征"的能力。 WKW_KWK 的核心价值是将高维语义空间映射到专门负责"位置匹配"的低维空间,提升位置感知的精确度,让 RoPE 作用于更关键的位置特征上。
4. 为何只对 K 做 RoPE,不对 V 做?
Attention 机制的本质分工,Attention 公式为 Softmax(QKT)VSoftmax(QK^T)VSoftmax(QKT)V :RoPE 的作用是帮助 Q 精准匹配目标 K(确定"在哪儿"),完成权重分配;而 V 的核心作用是提供"内容信息"(确定"是什么")。
在 Transformer 架构中,给 V 加 RoPE 收益极小,还会破坏 V 的纯粹内容属性,因此 MLA 仅对 K 分支施加 RoPE。
四、Q 侧设计解析
MLA 中 Q 无需缓存,但仍采用" DOWN(H)DOWN(H)DOWN(H) 压缩后再 UP(DOWN(H))UP(DOWN(H))UP(DOWN(H)) 还原"的逻辑, qR=RoPE(WQR⋅DOWN(H))q_R = RoPE(W_{QR} \cdot DOWN(H))qR=RoPE(WQR⋅DOWN(H)) 。
1. 无需缓存的 Q 为何要压缩?
核心考量:参数效率与训练稳定性:
-
参数效率提升 :KV 已压缩到低维潜空间 dcd_cdc ,Q 同步压缩可减少 WQW_QWQ 参数量(从 d×dd \times dd×d 简化为 d×dc+dc×dd \times d_c + d_c \times dd×dc+dc×d ),降低模型复杂度。
-
特征对齐与训练稳定:Q 与 KV 在同一潜空间完成特征匹配,让注意力机制抽象为"潜空间特征匹配",有助于模型处理超大规模上下文,提升训练稳定性。
2. 为何 q_R 不采用单独分支,而是基于压缩后的变量?
核心目标:降低推理延迟(Inference Latency):
Q 需实时计算,而压缩后的 cQ=DOWN(H)c_Q = DOWN(H)cQ=DOWN(H) 已在 Q 的计算流程中生成。基于 cQc_QcQ 进行 WQRW_{QR}WQR 投影得到 qRq_RqR ,可复用 cQc_QcQ 结果,避免从高维 HHH 重新执行大矩阵乘法,显著减少计算量,提升推理速度。若采用单独分支预测,需额外对高维 HHH 计算,增加冗余开销。