红黑树主要功能实现

红黑树

前提：二叉搜索树

根和叶子节点都是黑色
没有连续的两个红色节点
任意一条路径的黑色节点数相同
最长路径不超过最短路径的两倍

定义

scss 复制代码

struct rb_treeNode {
	int data;
	NodeColor Color;
	rb_treeNode* left;
	rb_treeNode* right;
	rb_treeNode* parent;

	rb_treeNode(int val)
		: data(val), Color(Red), left(nullptr), right(nullptr), parent(nullptr) {
	}
};
using Rb_treeNode = rb_treeNode*; // 或 typedef rb_treeNode* Rb_treeNode;

由于是初始模板，暂且定义数据类型为int，后续会通过泛型进行优化

插入

插入节点默认为红色，且只可能违反根叶黑或者不红红

如果插入黑色节点，则必然会违反黑路同的性质，维护所做的操作会更繁琐

具体步骤：

红黑树本质上是一种二叉搜索树，所以插入时和二叉搜索树是一样的
插入后进行维护操作

ini 复制代码

void insert(Rb_treeNode& root, int value) {
	// 情况1：空树
	if (root == nullptr) {
		root = new rb_treeNode(value);
		root->Color = Black; // 根必须为黑色
		return;
	}

	// 情况2：非空树，先找到插入位置
	rb_treeNode* cur = root;
	rb_treeNode* parent = nullptr;

	while (cur != nullptr) {
		if (cur->data == value) {
			std::cout << "数据重复，插入失败: " << value << std::endl;
			return; // 不插入重复值
		}
		parent = cur;
		if (value < cur->data) {
			cur = cur->left;
		}
		else {
			cur = cur->right;
		}
	}

	// 创建新节点
	cur = new rb_treeNode(value);
	cur->parent = parent;

	// 连接到父节点
	if (value < parent->data) {
		parent->left = cur;
	}
	else {
		parent->right = cur;
	}

	// 修复红黑树性质
	insertFixup(root, cur);

}

维护情况

第一种：插入节点是根节点

直接将根节点变为黑色

第二种：插入节点的叔叔的红色

如果叔叔节点是红色，那么父节点也必然是红色

我们需要对叔叔节点和父节点以及爷爷节点进行变色，让爷爷结点变成插入节点，由下而上对红黑树的颜色进行调整

ini 复制代码

while (cur != root && cur->parent != nullptr && cur->parent->Color == Red) {
	//左子树的节点
	if (cur->parent->parent->left == cur->parent) {
		//叔叔节点红色
		Rb_treeNode uncle = cur->parent->parent->right;
		if (uncle != nullptr && uncle->Color == Red) {
			uncle->Color = Black;
			cur->parent->Color = Black;
			cur->parent->parent->Color = Red;
			cur = cur->parent->parent;
		}

第三种：插入节点的叔叔是黑色（空节点）

LL型：右旋

右旋完成后对原父节点和爷爷节点进行变色

RR型同理

LR型：先左旋父节点，再右旋爷爷节点，再对插入节点和爷爷节点进行变色

rust 复制代码

while (cur != root && cur->parent != nullptr && cur->parent->Color == Red) {
	//左子树的节点
	if (cur->parent->parent->left == cur->parent) {
		//叔叔节点红色
		Rb_treeNode uncle = cur->parent->parent->right;
		if (uncle != nullptr && uncle->Color == Red) {
			uncle->Color = Black;
			cur->parent->Color = Black;
			cur->parent->parent->Color = Red;
			cur = cur->parent->parent;
		}
		//插入的叔叔节点是黑色
		else {
			//LR型
			if (cur == cur->parent->right) {
				cur = cur->parent;
				//可能旋转的是根节点
				Left_rotate(root, cur);
			}
			//LL型
			cur->parent->Color = Black;
			cur->parent->parent->Color = Red;
			//可能旋转的是根节点
			Right_rotate(root, cur->parent->parent);

		}
	}
	else {
		//右子树的节点
		Rb_treeNode uncle = cur->parent->parent->left;
		if (uncle != nullptr && uncle->Color == Red) {
			uncle->Color = Black;
			cur->parent->Color = Black;
			cur->parent->parent->Color = Red;
			cur = cur->parent->parent;
		}
		//插入的叔叔节点是黑色
		else {
			//RL型
			if (cur == cur->parent->left) {
				cur = cur->parent;
				//可能旋转的是根节点
				Right_rotate(root, cur);
			}
			//RR型
			cur->parent->Color = Black;
			cur->parent->parent->Color = Red;
			//可能旋转的是根节点
			Left_rotate(root, cur->parent->parent);

		}
	}
}
root->Color = Black; // ← 这行必不可少

删除

左右孩子都有

找直接前驱或者直接后驱进行替换，再对替换后的节点进行删除判断操作

注意：替换的时候只需进行值替换

ini 复制代码

// 情况 1：两个孩子 → 删除后继
if (cur->left != nullptr && cur->right != nullptr) {

	//y:指向后继节点
	y = BehindNode(cur);
	y_original_color = y->Color;
	cur->data = y->data;  // 只拷贝值
	//cur:指向换值的后继节点
	cur = y;
}

只有左孩子/只有右孩子

在这种情况下删除的结点只可能是黑色，其子结点为红色，如果是红黑的情况，那么这条路就会多出一个黑结点，如果是红红，则违反了红黑规则，如果是黑黑，同样这条路会多出一个黑色结点

这种情况下，我们的处理方案为：

将子节点替换到删除节点的位置，然后将节点变黑

ini 复制代码

// cur 至多只有一个孩子
if (cur->left != nullptr)
	x = cur->left;
else
	x = cur->right;

parent = cur->parent;

// 连接 parent 和 x
if (parent == nullptr) {
	root = x;
}
else if (cur == parent->left) {
	parent->left = x;
}
else {
	parent->right = x;
}

if (x != nullptr) {
	x->parent = parent;
}

没有孩子

如果是红节点：删除后无需任何调整，不需要进行修补

如果是黑节点：

这里我们要引入一个双黑节点的概念，当删除的节点是黑色而且其子节点也是黑色（叶子节点默认为黑色）时，因为删除后影响了黑路同的性质，在后续维护操作时不好设定条件，所以我们人为的将删除黑色节点后顶替上来的叶子节点设置为双重黑色，我们要做的就是消除双黑（遇到根节点或者遇到红节点），由于我没有设置哨兵节点，所以我消除双黑的方式就是将双黑的指针（空指针）指向根节点或者当其不为空且其颜色为红色时，这些都会在下面的情况中提到

所以外部循环为

arduino 复制代码

while (x != root && (x == nullptr || x->Color == Black))

1.1兄弟是黑色：兄弟至少有一个红孩子：

LL/RR：

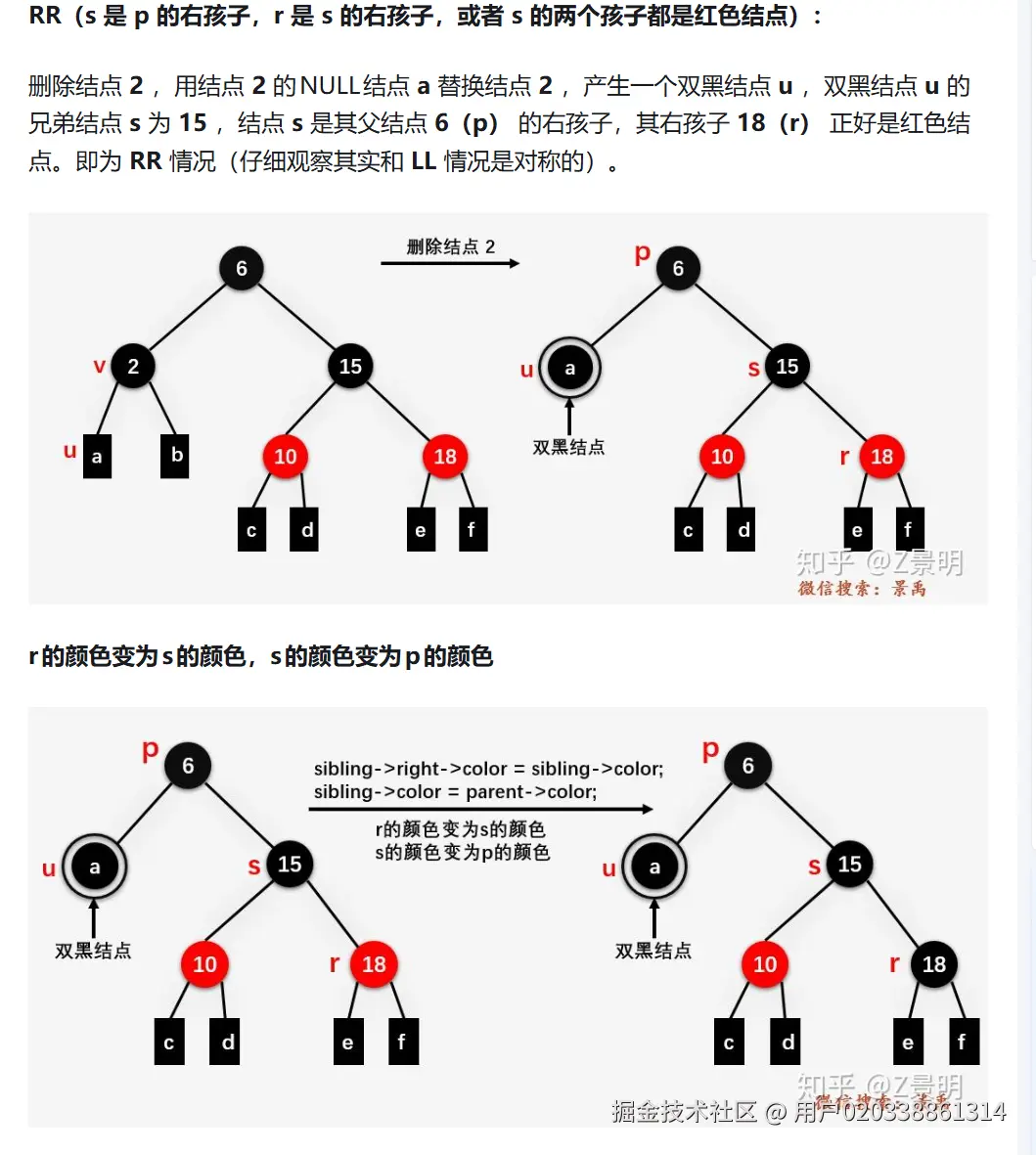
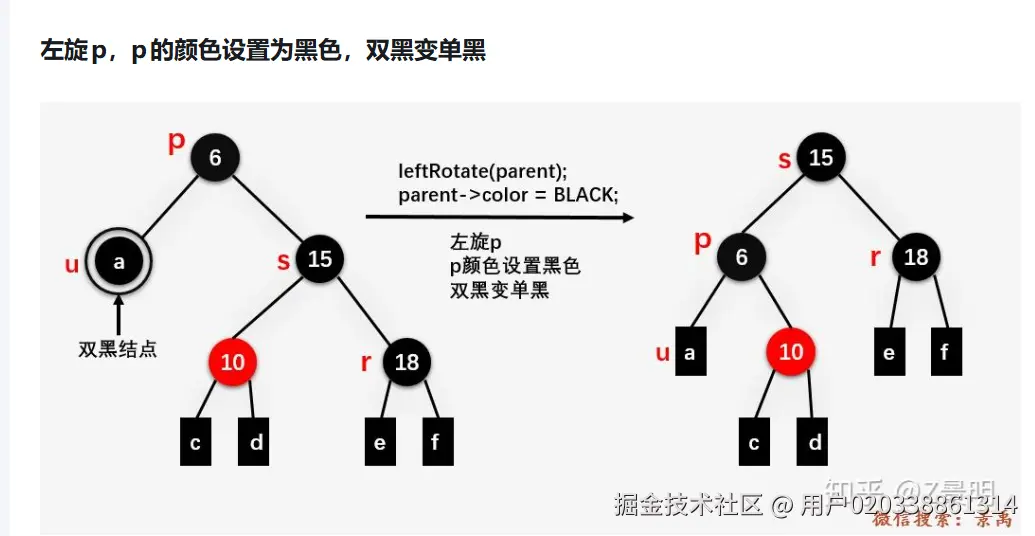
兄弟的两个孩子都是红孩子或者，兄弟只有左孩子/右孩子是红

左孩子/右孩子颜色变为父节点的颜色，父节点的颜色变为爷爷节点的颜色，爷爷节点的颜色变黑

双黑节点在旋转后设置为单黑节点（空节点）->指向根节点，修复完毕

ini 复制代码

//RR情况
else {
				w->right->Color = w->Color;
				w->Color = w->parent->Color;
				w->parent->Color = Black;
				Left_rotate(root, w->parent);
				//双黑调整为单黑
				x = root;
}

LR/RL：

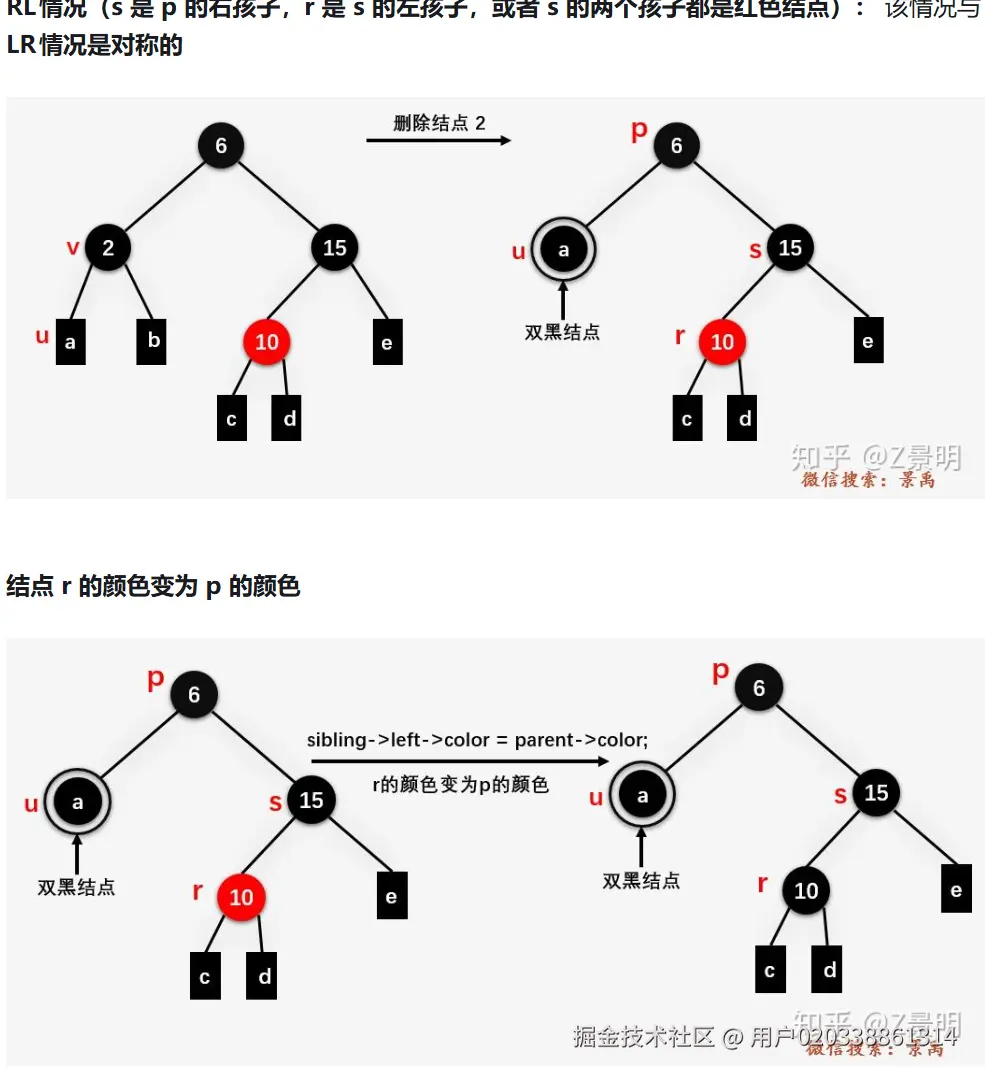
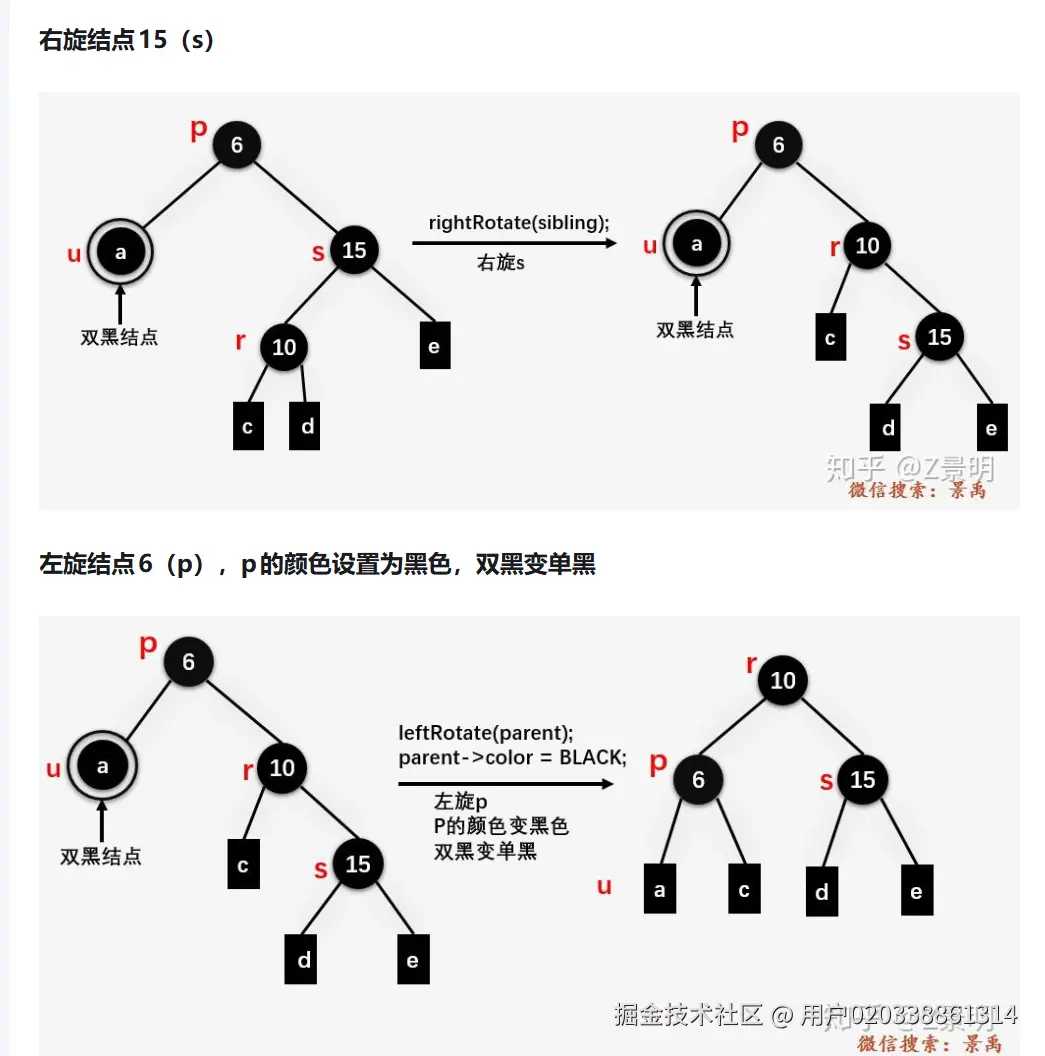
兄弟只有右孩子/左孩子

删掉的节点变为双黑节点

右孩子/左孩子颜色变为爷爷节点的颜色，爷爷节点变黑，左/右旋左/右孩子，然后右/左旋

双黑变单黑

ini 复制代码

// Case 3：RL型
if (w->right == nullptr || w->right->Color == Black) {
				if (w->left && w->parent) {
					Rb_treeNode original_parent = w->parent; // 保存原始父节点

					w->left->Color = original_parent->Color;
					original_parent->Color = Black;
					Right_rotate(root, w);
					Left_rotate(root, original_parent); // 明确旋转原始父节点
					x = root;
				}
}

注意：这种做法的话会使红黑树变成全黑，所以还有另一种解法：

解法二：

将这种情况转化为LL/RR型，使之至少有一个红节点（原兄弟节点），在进行操作

这样可以把两种情况合并起来，并且节点不是全黑

rust 复制代码

 else {
				// 情况3：x的兄弟节点是黑色的，兄弟的左孩子是红色，右孩子是黑色
				if (w->right->color == BLACK) {
					// 将左孩子涂黑
					w->left->color = BLACK;
					// 将兄弟节点变红
					w->color = RED;
					// 对兄弟节点右旋
					rbtree_right_rotate(T, w);
					// 重新设置x的兄弟节点
					w = x->parent->right;
				}
				// 情况4：x的兄弟节点是黑色；x的兄弟节点的右孩子是红色的
				// 将兄弟节点换成父节点的颜色
				w->color = x->parent->color;
				// 把父节点和兄弟节点的右孩子涂黑
				x->parent->color = BLACK;
				w->right->color = BLACK;
				// 对父节点做左旋
				rbtree_left_rotate(T, x->parent);
				// 设置x指针，指向根节点
				x = T->root;
			}

由于这两种情况是对称的，所以分为删除节点在左子树还是右子树两种情况

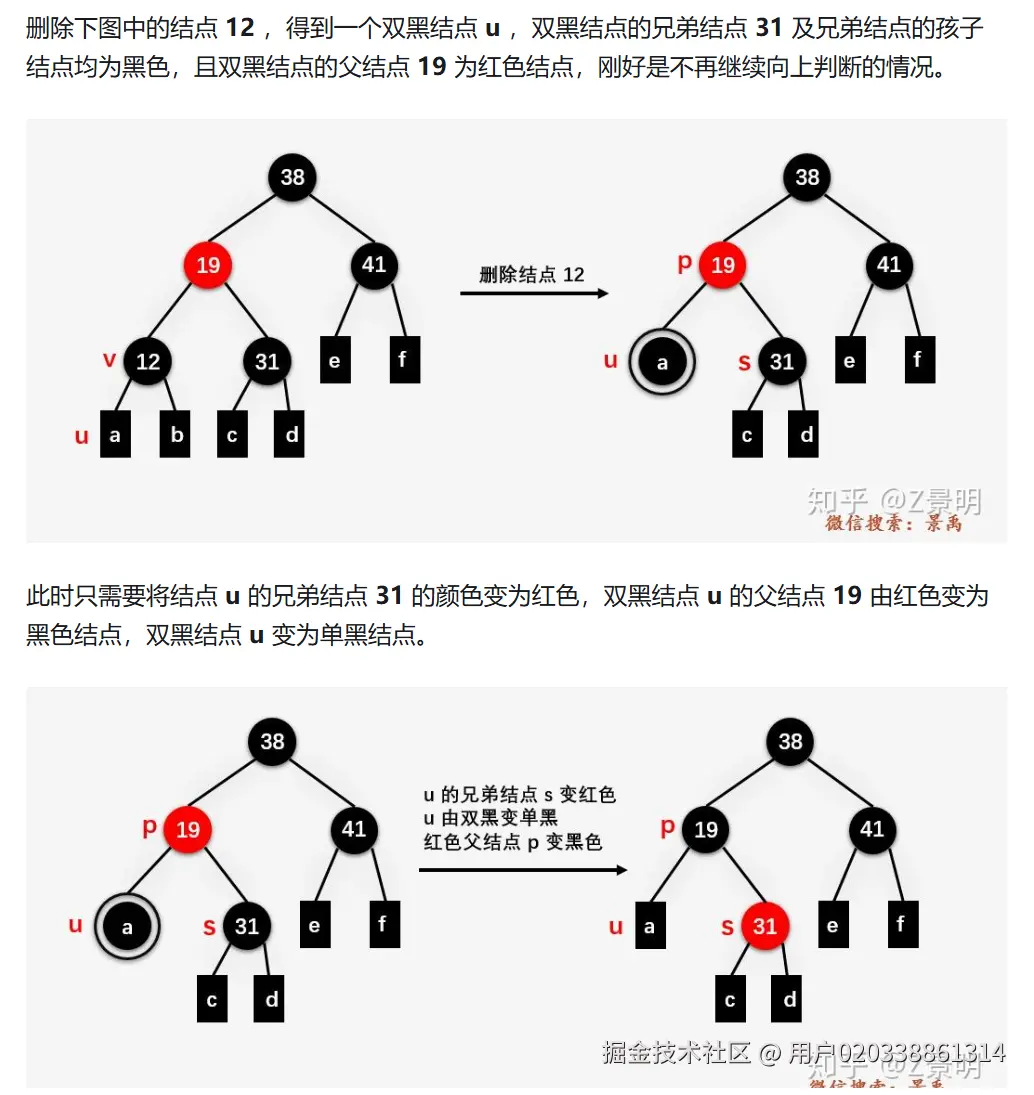
1.2兄弟的孩子都是黑色

兄弟变红，双黑上移（遇到红或根变为单黑）

如果遇到非根非红的普通节点，需要继续修复（LL,LR,RR,RL）

ini 复制代码

// Case 2：兄弟黑，两个孩子都黑
if ((w == nullptr) ||
	((w->left == nullptr || w->left->Color == Black) &&
		(w->right == nullptr || w->right->Color == Black))) {

	if (w) w->Color = Red;
	x = parent;
	parent = parent->parent;
}

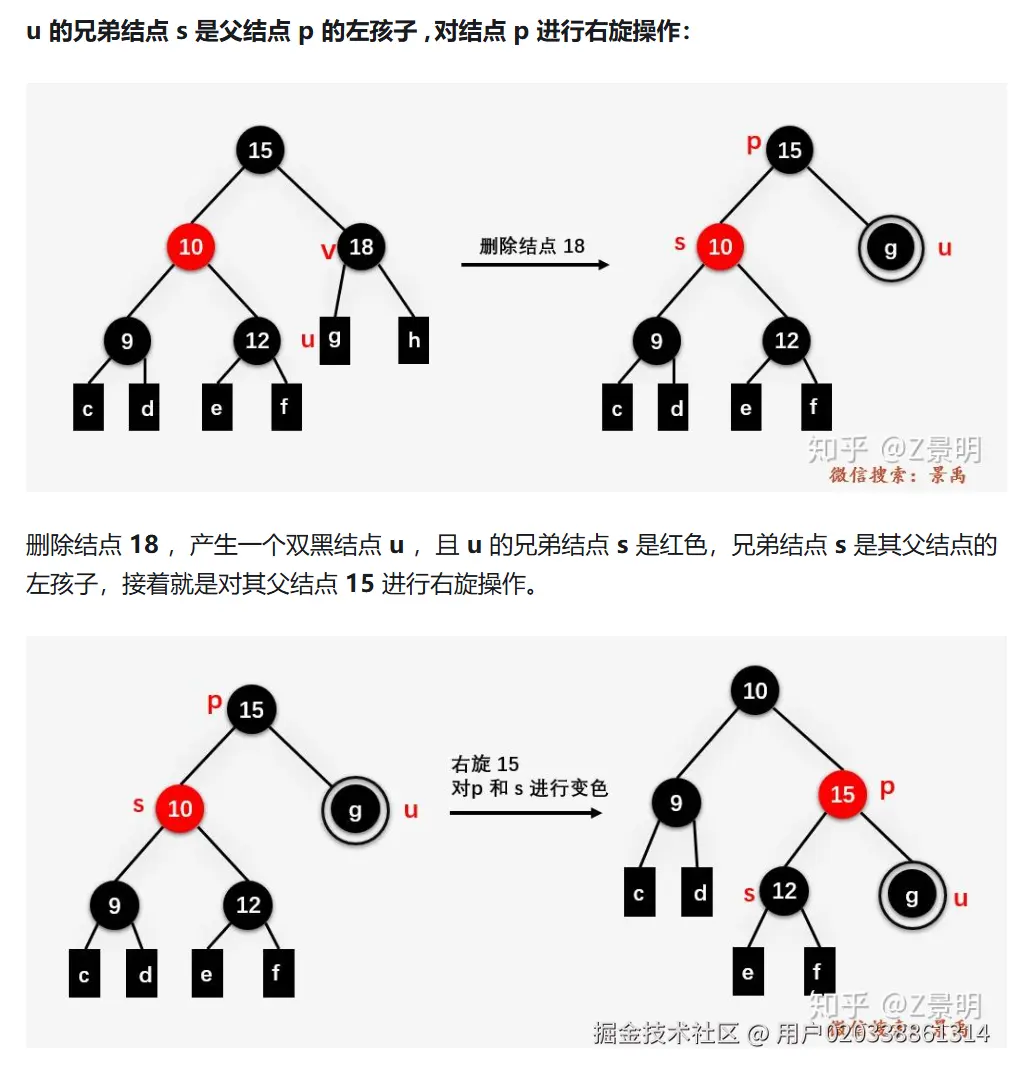
2.兄弟是红色，兄父变色，朝双黑旋转（保持双黑继续调整）

出现这种情况时，在变完色之后将双黑节点的父节点进行左旋/右旋，旋转完成之后根据双黑节点的位置进行调整，可能会出现上述1.2的情况

ini 复制代码

// Case 1：兄弟红
if (w && w->Color == Red) {
	w->Color = Black;
	parent->Color = Red;
	Left_rotate(root, parent);
	w = parent->right;
}

由于上述操作都是对称的，所以都需要区分左子树和右子树

优化处理

泛型优化

由于数据是int类型的，使用情况有限，我们可以使用泛型指定一个key用来当作比较数据在红黑树中存储，再指定另一个数据作为真正存储的数据通过key,value构成一个键值对

arduino 复制代码

template<typename Key, typename Value>
struct rb_treeNode {
    Key key;
    Value value;
    NodeColor Color;
    rb_treeNode* left;
    rb_treeNode* right;
    rb_treeNode* parent;

    rb_treeNode(const Key& k, const Value& v)
        : key(k), value(v), Color(Red), left(nullptr), right(nullptr), parent(nullptr) {
    }
};

template<typename Key, typename Value>
class RedBlackTree {
private:
    rb_treeNode<Key, Value>* root;
    //封装各种方法
    }

可以在RedBlackTree内部封装增删查改的方法，将辅助方法（如左旋，右旋操作）设置为private，将核心方法设置为public

这样就可以使用这个自己定义数据类型进行对数据的操作了

双黑节点优化

设置一个哨兵节点，让叶子节点直接指向该节点