Hadamard product {阿达玛乘积}
- [1. Definition](#1. Definition)
- [2. Properties](#2. Properties)
- [3. In programming languages](#3. In programming languages)
- References
In mathematics, the Hadamard product (also known as the element-wise product, entrywise product or Schur product) is a binary operation that takes in two matrices of the same dimensions and returns a matrix of the multiplied corresponding elements.
在数学中,阿达玛乘积 (Hadamard product,又译哈达玛乘积),又名舒尔乘积 (Schur product) 或逐项乘积 (entrywise product),是一个二元运算,其输入为两个相同形状的矩阵,输出是具有同样形状的、各个位置的元素等于两个输入矩阵相同位置元素的乘积的矩阵。
entry ['entri]
n. 记录;词条;登录;录入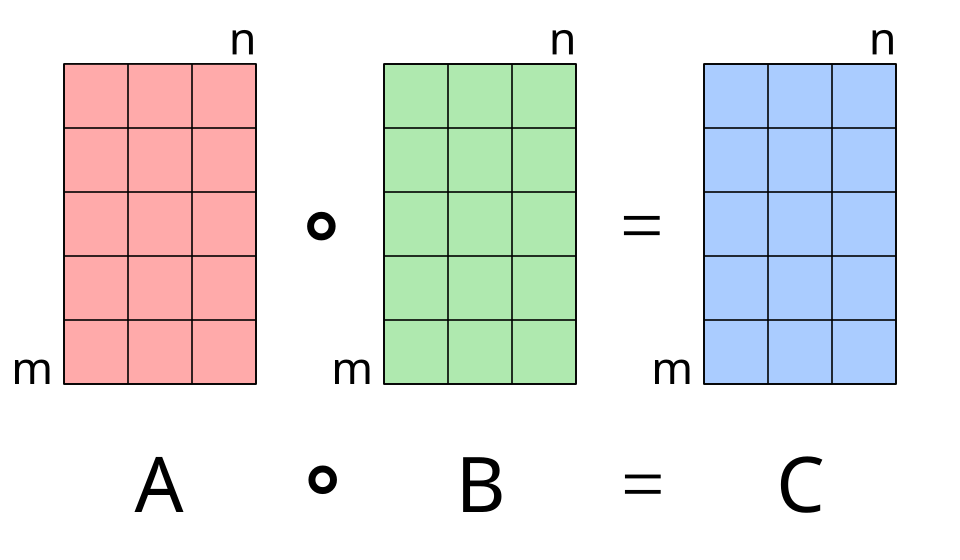
The Hadamard product operates on identically shaped matrices and produces a third matrix of the same dimensions.
1. Definition
For two matrices A \mathbf {A} A and B \mathbf {B} B of the same dimension m × n m \times n m×n, the Hadamard product A ⊙ B \mathbf {A} \odot \mathbf {B} A⊙B (sometimes A ∘ B \mathbf {A} \circ \mathbf {B} A∘B) is a matrix of the same dimension as the operands, with elements given by
( A ⊙ B ) i j = ( A ) i j ( B ) i j . (\mathbf {A} \odot \mathbf {B}){ij} = (\mathbf {A}){ij} (\mathbf {B})_{ij}. (A⊙B)ij=(A)ij(B)ij.
For matrices of different dimensions ( m × n m \times n m×n and p × q p \times q p×q, where m ≠ p m \neq p m=p or n ≠ q n \neq q n=q), the Hadamard product is undefined.
3 × 3 3\times 3 3×3 矩阵 A \mathbf {A} A 与 3 × 3 3\times 3 3×3 矩阵 B \mathbf {B} B 的阿达玛乘积为:
a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 \] ∘ \[ b 11 b 12 b 13 b 21 b 22 b 23 b 31 b 32 b 33 \] = \[ a 11 b 11 a 12 b 12 a 13 b 13 a 21 b 21 a 22 b 22 a 23 b 23 a 31 b 31 a 32 b 32 a 33 b 33 \] . \\begin{bmatrix} a_{11} \& a_{12} \& a_{13}\\\\ a_{21} \& a_{22} \& a_{23}\\\\ a_{31} \& a_{32} \& a_{33} \\end{bmatrix} \\circ \\begin{bmatrix} b_{11} \& b_{12} \& b_{13}\\\\ b_{21} \& b_{22} \& b_{23}\\\\ b_{31} \& b_{32} \& b_{33} \\end{bmatrix} = \\begin{bmatrix} a_{11}\\, b_{11} \& a_{12}\\, b_{12} \& a_{13}\\, b_{13}\\\\ a_{21}\\, b_{21} \& a_{22}\\, b_{22} \& a_{23}\\, b_{23}\\\\ a_{31}\\, b_{31} \& a_{32}\\, b_{32} \& a_{33}\\, b_{33} \\end{bmatrix}. a11a21a31a12a22a32a13a23a33 ∘ b11b21b31b12b22b32b13b23b33 = a11b11a21b21a31b31a12b12a22b22a32b32a13b13a23b23a33b33 .
## 2. Properties
* The Hadamard product is commutative (when working with a commutative ring), associative, and distributive over addition.
阿达玛乘积满足交换律 (当使用交换环时), 结合律和对加法的分配律
That is, if A \\mathbf {A} A, B \\mathbf {B} B, and C \\mathbf {C} C are matrices of the same size, and k k k is a scalar:
A ⊙ B = B ⊙ A A ⊙ ( B ⊙ C ) = ( A ⊙ B ) ⊙ C A ⊙ ( B + C ) = A ⊙ B + A ⊙ C ( k A ) ⊙ B = A ⊙ ( k B ) = k ( A ⊙ B ) A ⊙ 0 = 0 ⊙ A = 0 \\begin{align} A \\odot B \&= B \\odot A \\\\ A \\odot (B \\odot C) \&= (A \\odot B) \\odot C \\\\ A \\odot (B + C) \&= A \\odot B + A \\odot C \\\\ (kA) \\odot B \&= A \\odot (kB) = k(A \\odot B) \\\\ A \\odot 0 \&= 0 \\odot A = 0 \\end{align} A⊙BA⊙(B⊙C)A⊙(B+C)(kA)⊙BA⊙0=B⊙A=(A⊙B)⊙C=A⊙B+A⊙C=A⊙(kB)=k(A⊙B)=0⊙A=0
## 3. In programming languages
**The NumPy numerical library interprets `a*b` or `a.multiply(b)` as the Hadamard product, and uses `a@b` or `a.matmul(b)` for the matrix product.**
## References
\[1\] Yongqiang Cheng (程永强),