主成分分析(PCA)
Principal Component Analysis
主要目标:降维,找到主元(主元就是一组比原始特征更有代表性、信息更集中的新特征)
降维
以二维为例,降维的目的就是找到一条轴,把所有的点投影到这个轴上,使得轴上的点投影后距离最大:
线性代数知识点
|-----------|---------------------------------------------------------------------------------------------------|
| 向量(数据、矩阵) | |
| 内积(乘法、投影) | |
| 均值 | |
| 方差 | |
| 协方差 | |
PCA针对协方差主要目标
对协方差矩阵进行特征值分解,使其在新的坐标系下变成对角矩阵。
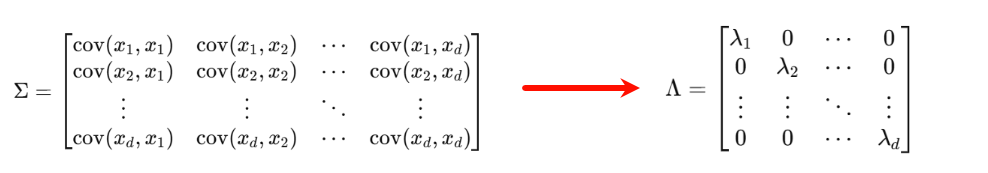
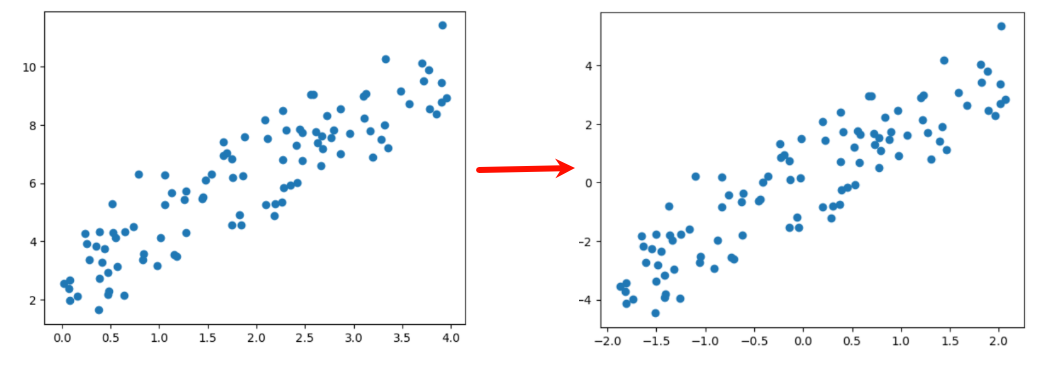
零均值化
左图(零均值化前):所有点 整体偏在右上角、数据"中心"不在原点 (0,0)
右图(零均值化后):点云 围绕原点分布、原点 (0,0)成了数据的"中心"
不改变点云的形状,只把整堆点从第一张图的位置,平移到第二张图那样以原点为中心
PCA求解算法
特征值()和特征向量(
):
步骤:
- 原始数据矩阵化
后,零均值化
- 求协方差矩阵
- 求协方差矩阵的特征值和特征向量
- 按特征值从大到小取特征向量前k行组成矩阵
即为降维后的数据
注意事项:
- 验证集和测试集执行同样的降维
- 验证集、测试集执行零均值化操作时,均值来自于训练集
- 保证训练集、测试集独立同分布一致性
主要作用:
- 有效缓解维度灾难
- 数据降噪效果好
- 降维后数据特征独立
- 无法解决过拟合
PCA的优缺点和适用条件
|---------|----------------------------------------------------------------------------------|------------------------------------------------------------------|----------------------------------------|
| 方法 | 优点 | 缺点 | 适用条件 |
| PCA | 简单容易计算,易于计算机实现 可以有效减少特征选择工作量,降低算法计算开销 不要求数据正态分布,无参数限制,不受样本标签限制 有效去除噪声,使得数据更加容易使用 | 非高斯分布情况下,PCA得到的主元可能非最优 特征值分解的求解方法有一定的局限性 降维后存在信息丢失 主成分解释较原数据比较模糊 | 变量间强相关性 数据压缩、预处理 数据降维、噪声去除 高维数据集探索与可视化 |