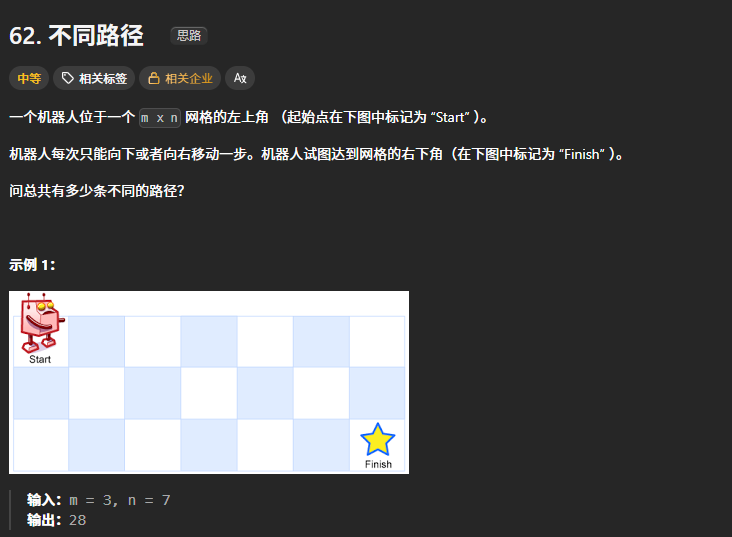
62.不同路径
- 确定dp数组(dp table)以及下标的含义
dp(m,n)是到达(m,n)时,有多少种可能的路径
- 确定递推公式
dp(m,n) = dp(m-1,n) + dp(m,n-1)
- dp数组如何初始化
dp(1,0)= 1,dp(0,1) = 1
- 确定遍历顺序
由dp(m,n) = dp(m-1,n) + dp(m,n-1),应该从起点向终点遍历
- 举例推导dp数组
需要注意:从起点开始(0,0),无论到达(k,0)或(0,k)都只有一条路径,不要混淆了
python
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
@cache
def dp(m,n):
if n==0 or m==0:
return 1
return dp(m-1,n) + dp(m,n-1)
return dp(m-1,n-1)63. 不同路径 II

- 确定dp数组(dp table)以及下标的含义定义
dp[i][j]表示从起点(0,0)到达位置(i,j)的不同路径数。
- 确定递推公式
如果该位置是障碍物:
dp[i][j] = 0如果不是障碍物:
dp[i][j] = dp[i-1][j] + dp[i][j-1]
- dp数组如何初始化
dp(1,0)= 1,dp(0,1) = 1,遇到障碍时,路径数量应该为0
- 确定遍历顺序
由dp(m,n) = dp(m-1,n) + dp(m,n-1),应该从起点向终点遍历
- 举例推导dp数组
在相对特殊的情况没想清楚,例如边缘上有障碍物,且仅有该道路时,应该也设为0。如[[0,1,0,0]]
同时,由于输入时m-1和n-1,存在越界可能,需要处理;
python
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
@cache
def dp(m,n):
if m<0 or n<0:
return 0
if obstacleGrid[m][n] == 1:
return 0
if n==0 and m==0:
return 1
return dp(m-1, n) + dp(m, n-1)
m = len(obstacleGrid)
n = len(obstacleGrid[0])
return dp(m-1,n-1)
相对标准的方法
python
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
m, n = len(obstacleGrid), len(obstacleGrid[0])
if obstacleGrid[0][0] == 1 or obstacleGrid[m-1][n-1] == 1:
return 0
dp = [[0] * n for _ in range(m)]
dp[0][0] = 1 # 起点
# 初始化第一列
for i in range(1, m):
if obstacleGrid[i][0] == 0: # 没有障碍物
dp[i][0] = dp[i-1][0] # 只能从上方来
# 初始化第一行
for j in range(1, n):
if obstacleGrid[0][j] == 0: # 没有障碍物
dp[0][j] = dp[0][j-1] # 只能从左方来
# 填充内部格子
for i in range(1, m):
for j in range(1, n):
if obstacleGrid[i][j] == 0: # 没有障碍物
dp[i][j] = dp[i-1][j] + dp[i][j-1]
# 有障碍物时保持0(默认值)
return dp[m-1][n-1]
整数拆分 (可跳过)
没有想得特别的清楚,仔细考虑一下:
- 确定dp数组(dp table)以及下标的含义定义
这里的dp数组也即给定的整数n目前为止还剩下多少
- 确定递推公式
dp[i] = max(j * dp[i-j] , j*(i-j), dp[i])
也即dp[i]是 i拆成的j和i-j的乘积或i拆成的i和dp(i-j)的乘积,或i本身
- dp数组如何初始化
因为n>=2,初始化dp(2)==1即可
- 确定遍历顺序
由dp[i] = max(j * dp[i-j] , j*(i-j), dp[i]),应该从起点向终点遍历
- 举例推导dp数组
python
class Solution:
def integerBreak(self, n: int) -> int:
dp = [0] * (n+1)
dp[2] = 1
for i in range(3,n+1):
for j in range(1,i-1):
dp[i] = max(j * dp[i-j] , j*(i-j), dp[i])
return dp[n]不同的二叉搜索树 (可跳过)
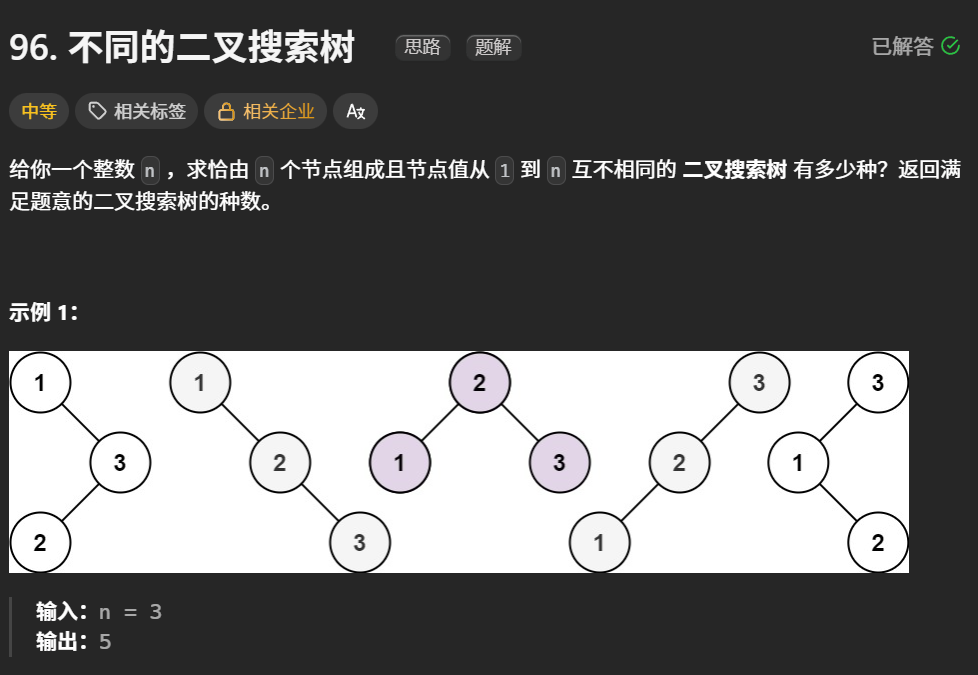
- 确定dp数组(dp table)以及下标的含义定义
dp(n)也即有n个节点的二叉搜索树有多少种
- 确定递推公式
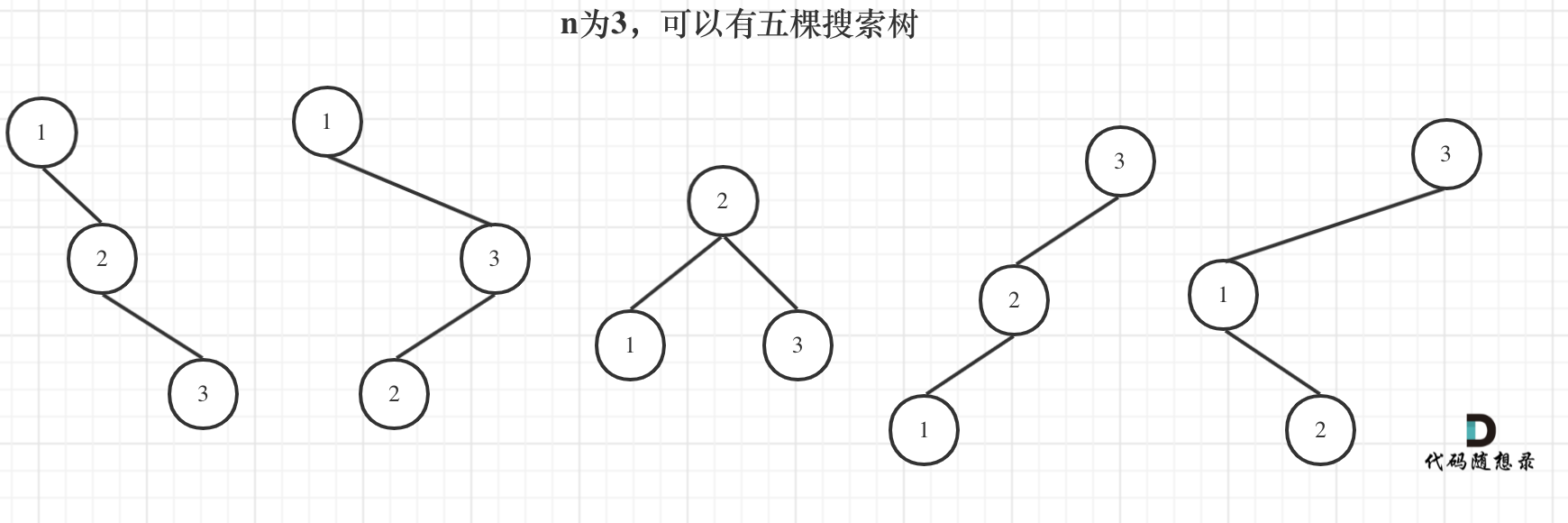
来看看n为3的时候,有哪几种情况。
当1为头结点的时候,其右子树有两个节点,看这两个节点的布局,是不是和 n 为2的时候两棵树的布局是一样的啊!
当3为头结点的时候,其左子树有两个节点,看这两个节点的布局,是不是和n为2的时候两棵树的布局也是一样的啊!
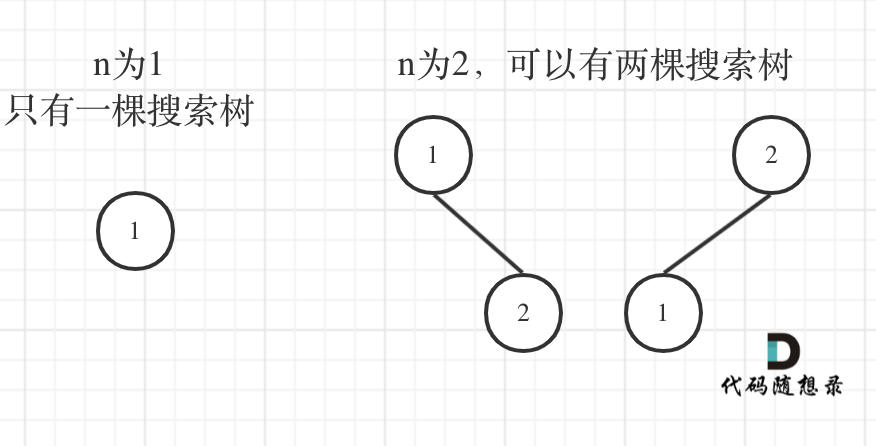
当2为头结点的时候,其左右子树都只有一个节点,布局是不是和n为1的时候只有一棵树的布局也是一样的啊!
发现到这里,其实我们就找到了重叠子问题了,其实也就是发现可以通过dp[1] 和 dp[2] 来推导出来dp[3]的某种方式。
思考到这里,这道题目就有眉目了。
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
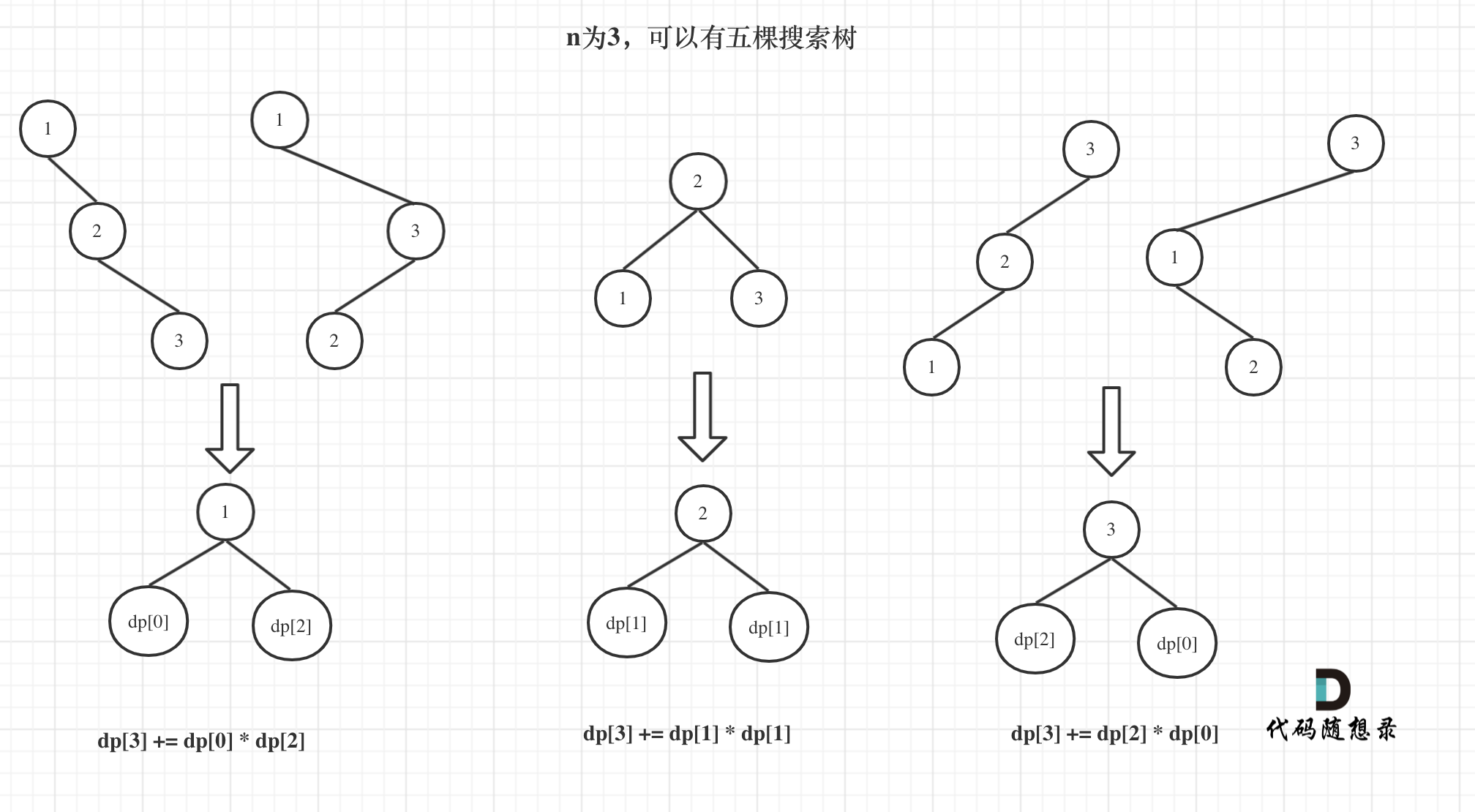
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
如图所示:
dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
j相当于是头结点的元素,从1遍历到i为止。
所以递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量
- dp数组如何初始化
初始化为0即可,其中dp[0] = 1
- 确定遍历顺序
顺序遍历即可
- 举例推导dp数组
python
class Solution:
def numTrees(self, n: int) -> int:
dp = [0] * (n+1)
dp[0] = 1
for i in range(1,n+1):
for j in range(1,i+1):
dp[i] += dp[j-1] * dp[i-j]
return dp[n]