Flutter 框架跨平台鸿蒙开发 - 井字棋游戏开发指南（含Minimax AI）

Flutter实战：井字棋游戏开发指南（含Minimax AI）

前言

井字棋（Tic-Tac-Toe）是最经典的策略游戏之一，规则简单但蕴含丰富的博弈论知识。这个项目不仅实现了双人对战，还包含了三种难度的AI对手，其中困难模式使用了经典的Minimax算法，是学习游戏AI的绝佳案例。

效果预览

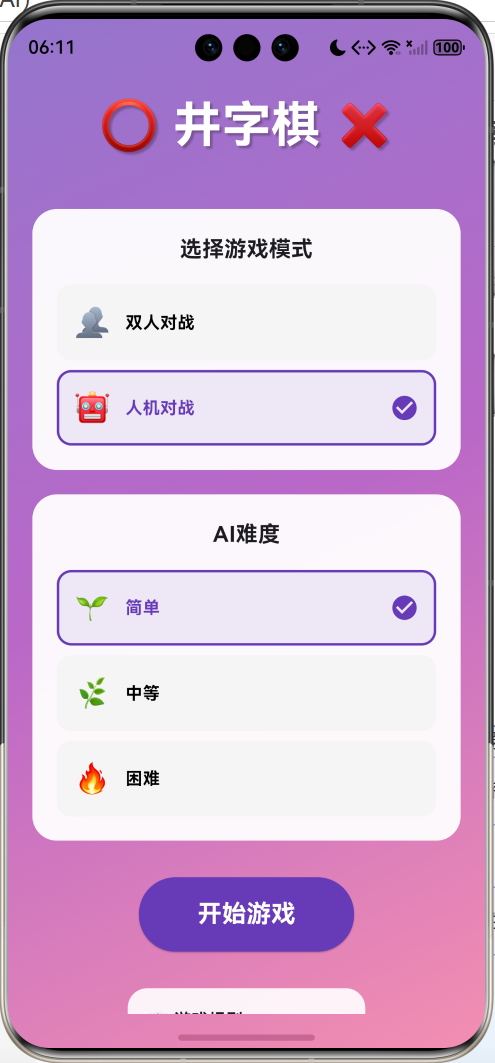
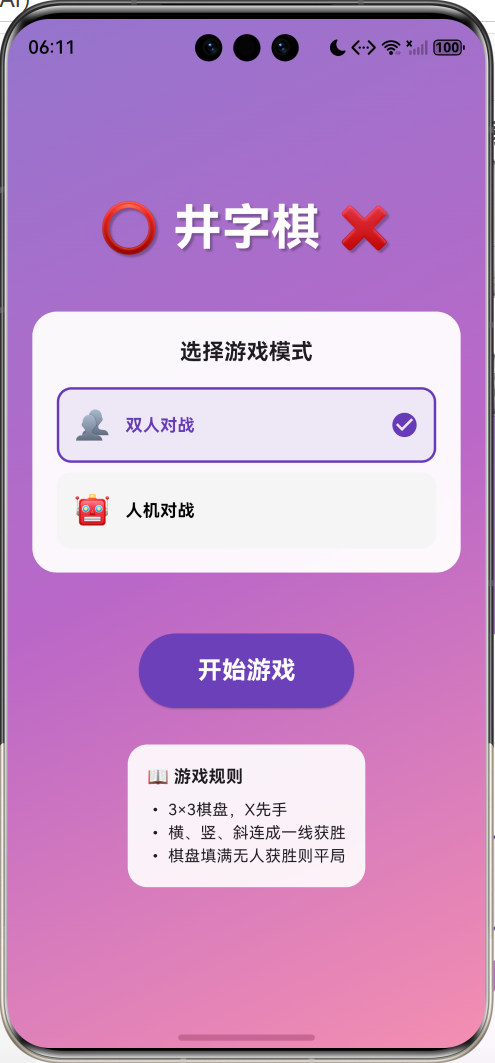
游戏特性：

双人对战（PVP）和人机对战（PVE）
三种AI难度（简单/中等/困难）
Minimax算法实现无敌AI
获胜动画和高亮
胜负平统计

技术架构

动画
AI系统
游戏逻辑
否
是
玩家落子
检查获胜
游戏结束?
切换玩家
显示结果
简单AI
随机落子
中等AI
简单策略
困难AI
Minimax算法
落子动画
缩放效果
获胜动画
高亮闪烁

核心数据结构

玩家枚举

dart 复制代码

enum Player {
  none,  // 空格
  x,     // X玩家
  o,     // O玩家
}

extension PlayerExtension on Player {
  String get symbol {
    switch (this) {
      case Player.x: return 'X';
      case Player.o: return 'O';
      case Player.none: return '';
    }
  }
  
  Color get color {
    switch (this) {
      case Player.x: return Colors.blue;
      case Player.o: return Colors.red;
      case Player.none: return Colors.grey;
    }
  }
  
  Player get opponent {
    switch (this) {
      case Player.x: return Player.o;
      case Player.o: return Player.x;
      case Player.none: return Player.none;
    }
  }
}

游戏状态

dart 复制代码

List<Player> _board = List.filled(9, Player.none);  // 棋盘状态
Player _currentPlayer = Player.x;                    // 当前玩家
Player? _winner;                                     // 获胜者
List<int> _winningLine = [];                        // 获胜连线
bool _isGameOver = false;                            // 游戏结束标志

获胜检测算法

获胜模式

对角线
0-4-8
2-4-6
纵向
0-3-6
1-4-7
2-5-8
横向
0-1-2
3-4-5
6-7-8

检测代码

dart 复制代码

List<int>? _checkWinnerForPlayer(Player player) {
  const List<List<int>> winPatterns = [
    [0, 1, 2], [3, 4, 5], [6, 7, 8], // 横向
    [0, 3, 6], [1, 4, 7], [2, 5, 8], // 纵向
    [0, 4, 8], [2, 4, 6],            // 对角线
  ];
  
  for (var pattern in winPatterns) {
    if (_board[pattern[0]] == player &&
        _board[pattern[1]] == player &&
        _board[pattern[2]] == player) {
      return pattern;  // 返回获胜连线
    }
  }
  return null;
}

AI实现

1. 简单AI - 随机落子

dart 复制代码

int _getRandomMove() {
  List<int> available = [];
  for (int i = 0; i < 9; i++) {
    if (_board[i] == Player.none) available.add(i);
  }
  return available[_random.nextInt(available.length)];
}

最简单的策略，从所有空位中随机选择一个。

2. 中等AI - 简单策略

dart 复制代码

int _getMediumMove() {
  // 1. 先尝试获胜
  int? winMove = _findWinningMove(Player.o);
  if (winMove != null) return winMove;
  
  // 2. 再阻止对手获胜
  int? blockMove = _findWinningMove(Player.x);
  if (blockMove != null) return blockMove;
  
  // 3. 否则随机
  return _getRandomMove();
}

int? _findWinningMove(Player player) {
  for (int i = 0; i < 9; i++) {
    if (_board[i] == Player.none) {
      _board[i] = player;
      bool wins = _checkWinnerForPlayer(player) != null;
      _board[i] = Player.none;
      if (wins) return i;
    }
  }
  return null;
}

策略优先级：

如果能一步获胜，直接获胜
如果对手能一步获胜，阻止对手
否则随机落子

3. 困难AI - Minimax算法

算法原理

Minimax是一种零和博弈的决策算法，通过递归搜索所有可能的走法，选择对自己最有利的一步。
是
否
AI
玩家
当前局面
游戏结束?
返回评分
轮到谁?
最大化评分
最小化评分
遍历所有可能
遍历所有可能
递归调用
返回最优评分

评分系统

S c o r e = { 10 − d e p t h AI获胜 d e p t h − 10 玩家获胜 0 平局 Score = \begin{cases} 10 - depth & \text{AI获胜} \\ depth - 10 & \text{玩家获胜} \\ 0 & \text{平局} \end{cases} Score=⎩ ⎨ ⎧10−depthdepth−100AI获胜玩家获胜平局

AI获胜：正分，越快获胜分数越高
玩家获胜：负分，越快输掉分数越低
平局：0分

实现代码

dart 复制代码

int _getBestMove() {
  int bestScore = -1000;
  int bestMove = 0;
  
  // 遍历所有空位
  for (int i = 0; i < 9; i++) {
    if (_board[i] == Player.none) {
      _board[i] = Player.o;
      int score = _minimax(_board, 0, false);
      _board[i] = Player.none;
      
      if (score > bestScore) {
        bestScore = score;
        bestMove = i;
      }
    }
  }
  
  return bestMove;
}

int _minimax(List<Player> board, int depth, bool isMaximizing) {
  // 检查终止条件
  List<int>? winLine = _checkWinnerForPlayer(Player.o);
  if (winLine != null) return 10 - depth;  // AI赢
  
  winLine = _checkWinnerForPlayer(Player.x);
  if (winLine != null) return depth - 10;  // 玩家赢
  
  if (_isBoardFull()) return 0;  // 平局
  
  if (isMaximizing) {
    // AI回合，最大化评分
    int bestScore = -1000;
    for (int i = 0; i < 9; i++) {
      if (board[i] == Player.none) {
        board[i] = Player.o;
        int score = _minimax(board, depth + 1, false);
        board[i] = Player.none;
        bestScore = max(bestScore, score);
      }
    }
    return bestScore;
  } else {
    // 玩家回合，最小化评分
    int bestScore = 1000;
    for (int i = 0; i < 9; i++) {
      if (board[i] == Player.none) {
        board[i] = Player.x;
        int score = _minimax(board, depth + 1, true);
        board[i] = Player.none;
        bestScore = min(bestScore, score);
      }
    }
    return bestScore;
  }
}

Minimax搜索树示例

当前局面

评分: ?
走法1

评分: 10
走法2

评分: 0
走法3

评分: -10
对手走法1

评分: 10
对手走法2

评分: 8
对手走法1

评分: 0
对手走法2

评分: 0
对手走法1

评分: -10
对手走法2

评分: -8

AI选择评分最高的走法1。

动画系统

落子动画

dart 复制代码

late AnimationController _scaleController;

_scaleController = AnimationController(
  vsync: this,
  duration: const Duration(milliseconds: 200),
);

// 落子时触发
void _makeMove(int index) {
  setState(() {
    _board[index] = _currentPlayer;
    _lastMove = index;
  });
  
  _scaleController.forward().then((_) => _scaleController.reverse());
}

// 渲染
AnimatedBuilder(
  animation: _scaleController,
  builder: (context, child) {
    final scale = isLastMove 
      ? 1.0 + (_scaleController.value * 0.2)
      : 1.0;
    
    return Transform.scale(
      scale: scale,
      child: cellWidget,
    );
  },
)

获胜动画

dart 复制代码

late AnimationController _winController;

_winController = AnimationController(
  vsync: this,
  duration: const Duration(milliseconds: 500),
);

// 获胜时触发
void _onGameOver() {
  _winController.forward();
}

// 渲染获胜格子
final scale = isWinningCell 
  ? 1.0 + (_winController.value * 0.1) 
  : 1.0;

游戏流程

PVE
PVP
有人获胜
无人获胜
棋盘填满
PVE且轮到AI
继续
开始界面
选择模式
选择难度
游戏进行
玩家落子
检查获胜
游戏结束
检查平局
AI落子
显示结果
再来一局
返回菜单

算法复杂度分析

时间复杂度

算法	最坏情况	平均情况	说明
随机AI	O(n)	O(n)	n为空位数
中等AI	O(n²)	O(n²)	需要检查每个位置
Minimax	O(9!)	O(9!)	搜索所有可能

空间复杂度

算法	复杂度	说明
随机AI	O(n)	存储空位列表
中等AI	O(1)	常数空间
Minimax	O(n)	递归栈深度

Minimax优化

井字棋的状态空间较小（最多9! = 362,880种状态），Minimax可以在毫秒级完成。对于更复杂的游戏，可以使用：

Alpha-Beta剪枝 - 减少搜索节点
深度限制 - 限制搜索深度
置换表 - 缓存已计算的局面

Alpha-Beta剪枝（扩展）

dart 复制代码

int _alphabeta(List<Player> board, int depth, int alpha, int beta, bool isMaximizing) {
  // 终止条件检查...
  
  if (isMaximizing) {
    int maxEval = -1000;
    for (int i = 0; i < 9; i++) {
      if (board[i] == Player.none) {
        board[i] = Player.o;
        int eval = _alphabeta(board, depth + 1, alpha, beta, false);
        board[i] = Player.none;
        maxEval = max(maxEval, eval);
        alpha = max(alpha, eval);
        if (beta <= alpha) break;  // Beta剪枝
      }
    }
    return maxEval;
  } else {
    int minEval = 1000;
    for (int i = 0; i < 9; i++) {
      if (board[i] == Player.none) {
        board[i] = Player.x;
        int eval = _alphabeta(board, depth + 1, alpha, beta, true);
        board[i] = Player.none;
        minEval = min(minEval, eval);
        beta = min(beta, eval);
        if (beta <= alpha) break;  // Alpha剪枝
      }
    }
    return minEval;
  }
}

博弈论分析

完美对局

在双方都采用最优策略的情况下，井字棋必然是平局。
先手X
中心
角落
边
后手O最优应对
后手O最优应对
后手O最优应对
平局

策略优先级

中心优先 - 控制中心有4条线
角落次之 - 角落有3条线
边最弱 - 边只有2条线

扩展思路

井字棋扩展
变体玩法
4×4井字棋
3D井字棋
五子棋
连珠
AI增强
蒙特卡洛树搜索
神经网络
强化学习
开局库
功能扩展
在线对战
录像回放
局面分析
提示系统
视觉效果
3D渲染
粒子特效
音效反馈
主题皮肤

总结

这个井字棋游戏实现了完整的游戏体验和AI系统，核心技术点包括：

Minimax算法 - 经典的博弈树搜索算法
枚举扩展 - 使用extension为枚举添加方法
动画系统 - 落子和获胜的视觉反馈
AI分级 - 三种难度满足不同水平玩家
状态管理 - 清晰的游戏状态流转

井字棋虽然简单，但Minimax算法的思想可以应用到象棋、围棋等更复杂的游戏中，是学习游戏AI的最佳入门案例。
欢迎加入开源鸿蒙跨平台社区：https://openharmonycrossplatform.csdn.net