目录
[为什么是 "单点" ,而非 "多点" ?](#为什么是 “单点” ,而非 “多点” ?)
[高阶敏感的 "负面效应"](#高阶敏感的 “负面效应”)
[高阶敏感的 "正面效应"](#高阶敏感的 “正面效应”)

泰勒级数:"多阶导数"、"多维特征"
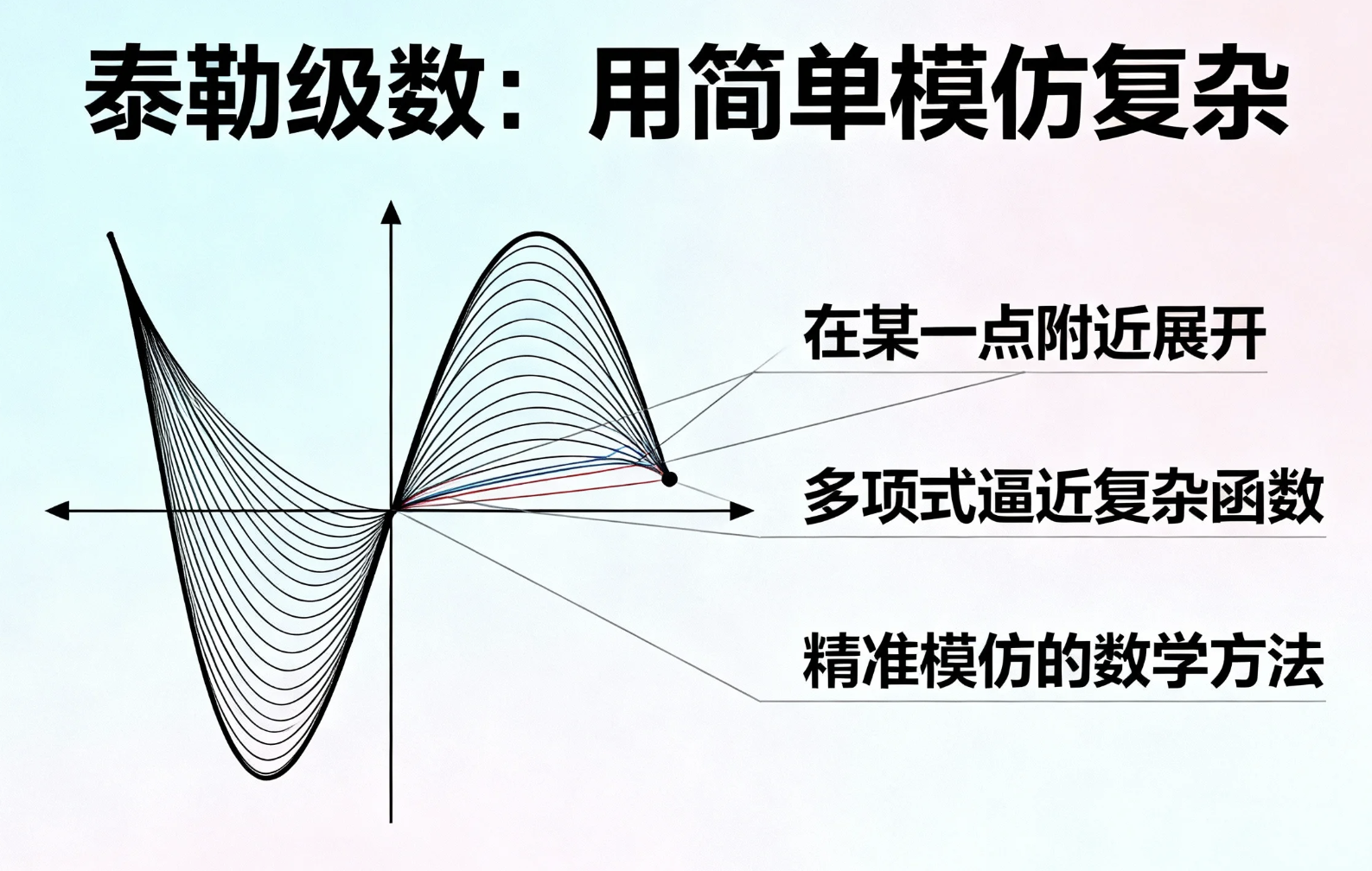
泰勒级数,就是在一个点附近,用多项式去精准模仿复杂函数的方法。是"用简单模仿复杂"。
我们程序员都知道,计算机最擅长加减乘除,可现实里的 sinx 、 e^x 这类函数,它根本"看不懂"。泰勒级数的思路就很绝:从一个点里榨取足够多的细节,把复杂函数拆成一堆加减乘除的多项式。
这里的"细节",可以直观地把它理解为单点的多个平行维度特征------比如观察一个像素,亮度、水平亮度变化、垂直亮度变化就是三个维度;观察一个人,身高、体重、肤色就是三个维度。
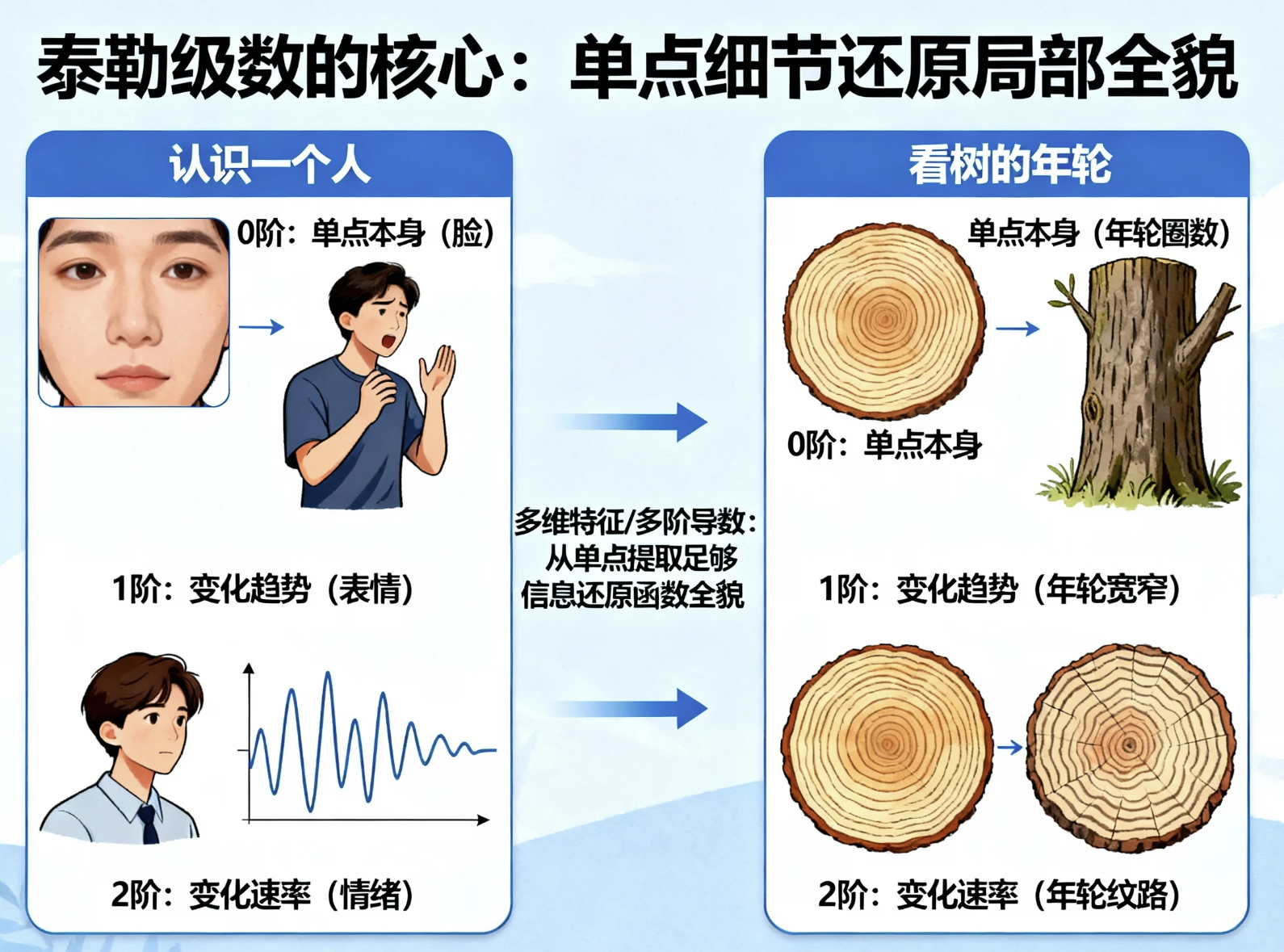
用数学上的严谨表述,是从变化深度划分的"多阶导数":
0阶信息:点的函数值(像素亮度、人的当前位置),是最基础的"存在状态";
1阶信息:函数变化率(亮度变化趋势、人的跑步速度),描述"状态变化的快慢";
2阶信息:变化率的变化率(亮度变化曲率、人的加速度),描述"变化的剧烈程度";
更高阶信息:就是"变化的变化的变化......",层层深入刻画局部特征。
不管是"多维特征"还是"多阶导数",都是为了从一个点里挖出足够多的信息,还原这个点附近的函数全貌。泰勒级数的核心,就是用单点的"全部细节",还原局部的真实模样。

为什么是 "单点" ,而非 "多点" ?
为什么非要揪着一个点不放?用多个点分析,不是更全面吗?
其实,"多点分析"的方法已经就有了,叫插值。但插值有个致命短板------它只保证在选中的点上和原函数一致,点与点之间的走势完全是"猜"的,就像地图上标记了几个城市,却不知道城市之间的路是直是弯。
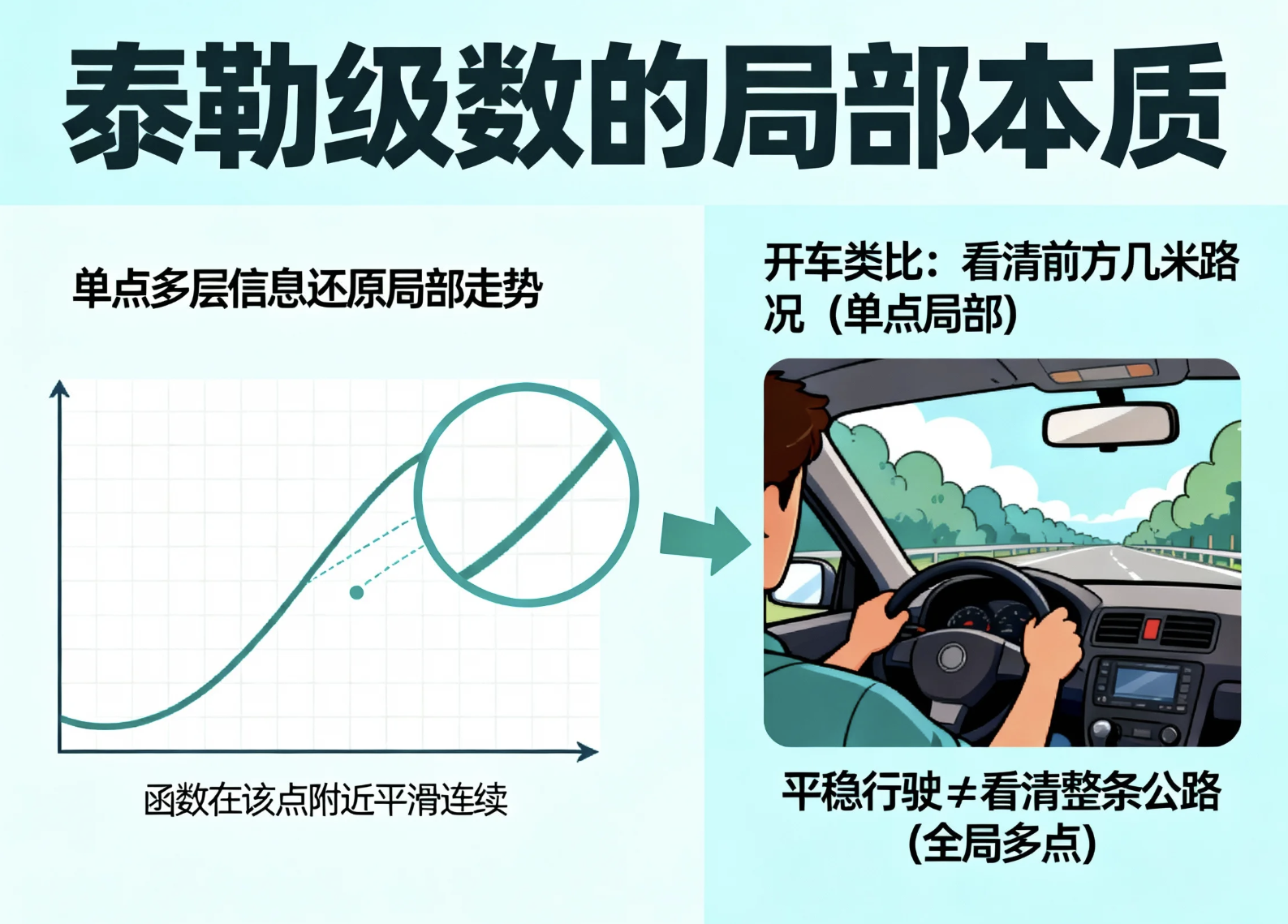
泰勒级数不一样,它抓的是函数的局部 本质。只要这个点附近的函数是平滑连续 的,就能靠单点的多层信息精准还原局部走势。它从设计之初就没打算"描述整条曲线",目标就是解决局部问题------这是理解泰勒级数的第一个关键。
就像开车时,你只需要看清前方几米的路况(单点局部),就能平稳行驶;不需要一下子看清整条公路(全局多点)。

高阶敏感的 "负面效应"
既然单点多层信息这么精准,插值的多点覆盖又这么全面,把两者结合------在多个点上都做泰勒级数的多层分析,岂不是既能全局覆盖,又能局部精准?
这个想法听起来完美,却殊不知,它会触发"龙格现象"。
简单说就是,当给多个点加上高阶导数条件,试图用高阶多项式拟合时,多项式会"疯掉 "。哪怕改动一个点的微小数据,整条曲线都会剧烈震荡 ,面目全非。
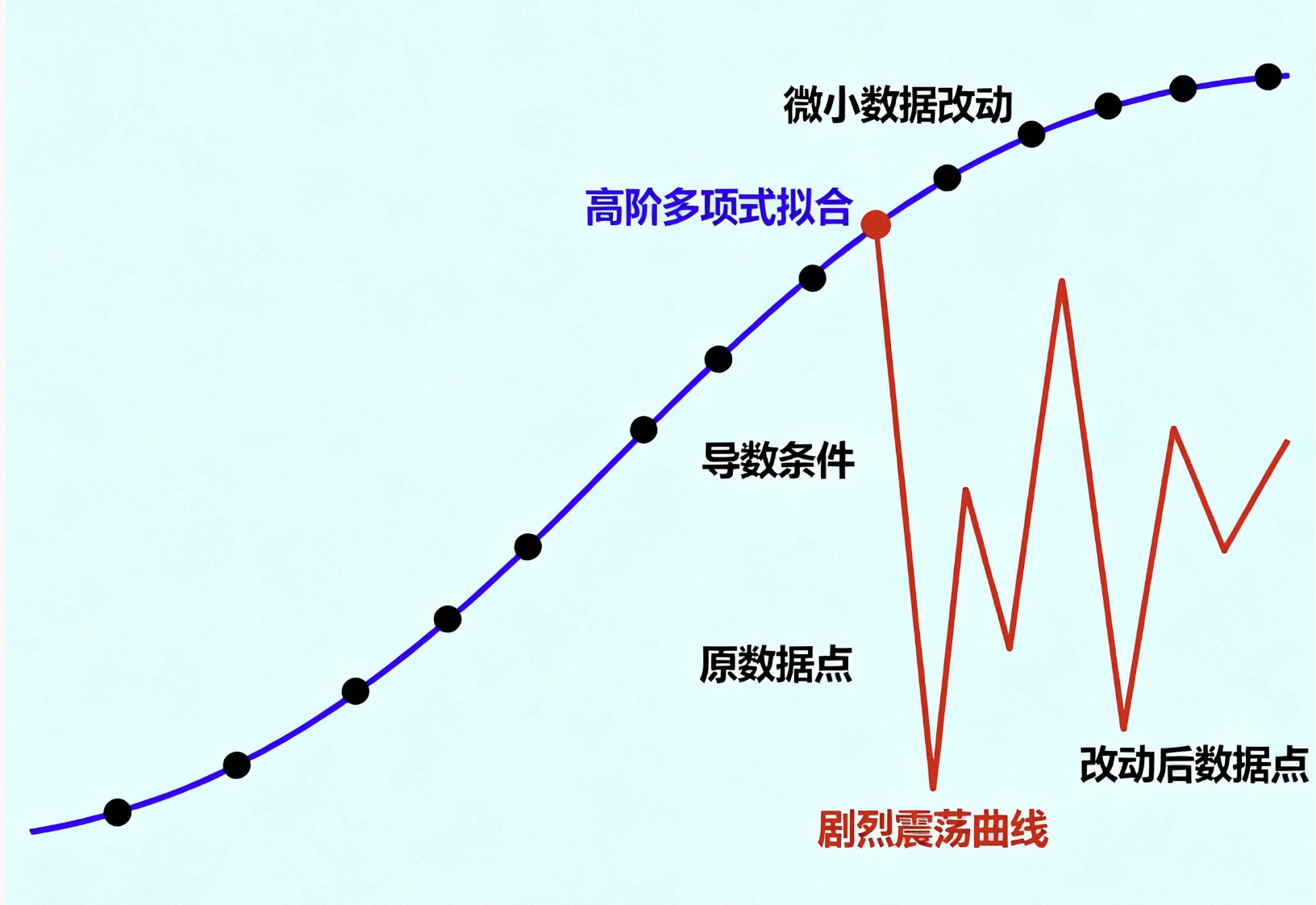
我想到自己画画的经历:画一条直线,手抖一点没关系;画一条20阶的复杂曲线,手抖0.1毫米,整条线就会歪到离谱。
背后的核心原因,是高阶项对噪声的极度敏感。
数学理论里的函数是完美无误差的,但工程数据永远有噪声------传感器偏差、仪器精度限制、环境干扰,都会带来微小误差。而高阶多项式会把这些误差放大到指数级别。

这就像用矮胖的杯子和细高的瓶子倒水:矮胖杯子(低阶多项式)怎么晃都不容易洒;细高瓶子(高阶多项式)稍微一动,水就溅得到处都是。
正因如此,工程里很少用高阶全局拟合,反而喜欢分段低阶逼近------把曲线切成很多小段,每段用低阶泰勒级数,既保证精准,又避免震荡。这才是泰勒级数在工程里的正确打开方式。

高阶敏感的 "正面效应"
高阶项只会带来麻烦吗?来看怎么让它的 缺点 变成 杀手锏:
用泰勒级数做CT图像边缘检测,对比了 普通Sobel边缘检测 和 泰勒增强边缘检测 ,核心处理:
cs
/// <summary>
/// 使用泰勒级数拟合局部邻域的亮度值
/// </summary>
public static double TaylorApproximation(
double f0, // 中心点亮度
double dx, double dy, // 一阶偏导数
double dxx, double dyy, double dxy, // 二阶偏导数
double offsetX, double offsetY) // 相对于中心点的偏移
{
double result = f0
+ dx * offsetX // 一阶项:水平方向变化
+ dy * offsetY // 一阶项:垂直方向变化
+ 0.5 * (dxx * offsetX * offsetX // 二阶项:水平曲率
+ 2 * dxy * offsetX * offsetY // 二阶项:混合曲率
+ dyy * offsetY * offsetY); // 二阶项:垂直曲率
return Math.Clamp(result, 0, 255);
}
private WriteableBitmap ApplyTaylorEnhancedEdgeDetec(byte[] sourceData, int width, int height)
{
for (int y = 1; y < height - 1; y++)
{
for (int x = 1; x < width - 1; x++)
{
// 计算一阶和二阶导数
var (dx, dy) = ImageProcessor.ComputeGradient(sourceData, width, height, x, y);
var (dxx, dyy, dxy) = ImageProcessor.ComputeSecondDerivatives(sourceData, width, height, x, y);
// 一阶梯度幅度(边缘强度)
double gradientMagnitude = Math.Sqrt(dx * dx + dy * dy);
// 二阶曲率(判断是真边缘还是噪声)
// 真边缘的二阶导数较大,噪声的二阶导数较小
double curvature = Math.Abs(dxx) + Math.Abs(dyy);
double curvatureThreshold = 10.0;
// 如果曲率大,说明是真边缘,增强
// 如果曲率小,可能是噪声,抑制
double edgeStrength = gradientMagnitude;
if (curvature > curvatureThreshold)
{
edgeStrength *= enhancementStrength; // 增强真边缘
}
else
{
edgeStrength *= 0.3; // 抑制噪声
}
}
}
}比对效果如下:
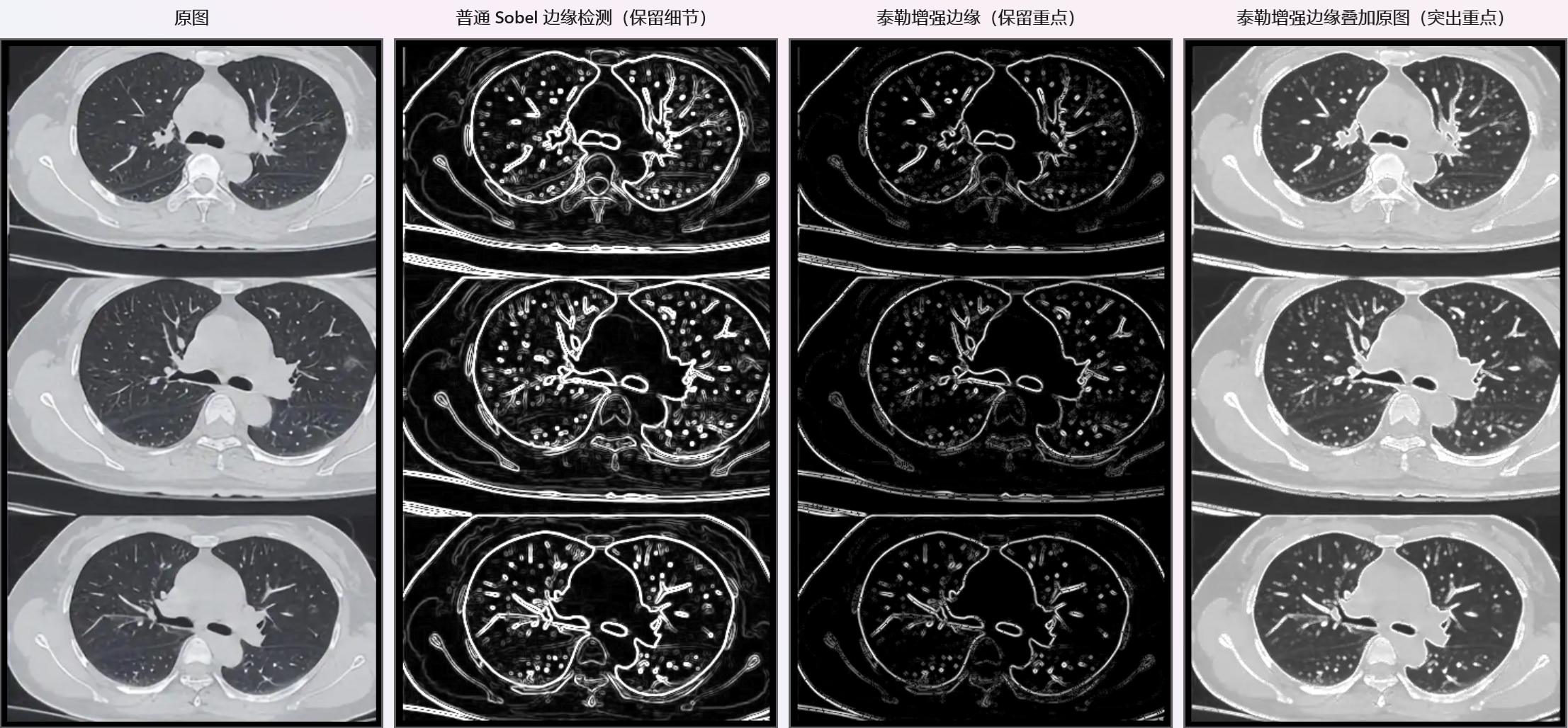
**Sobel检测:**只用到了一阶亮度变化率,所有细节全保留------包括物体轮廓、图像颗粒、传感器噪声,线条密密麻麻,有"流光感",艺术风格很强,但杂乱无章;
**泰勒增强:**结合了一阶变化率+二阶曲率,线条明显变少,很多细碎细节消失了,轮廓反而更突出、更干净。
泰勒增强怎么"丢了这么多细节"?这正式它的 "实用" 目标。
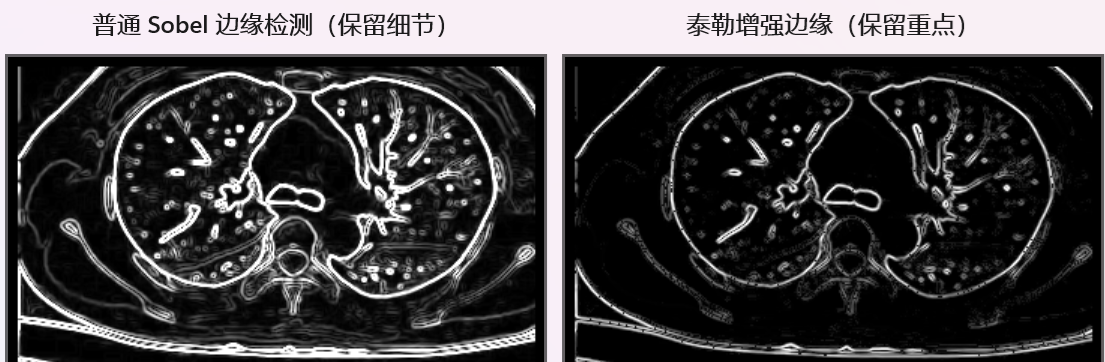
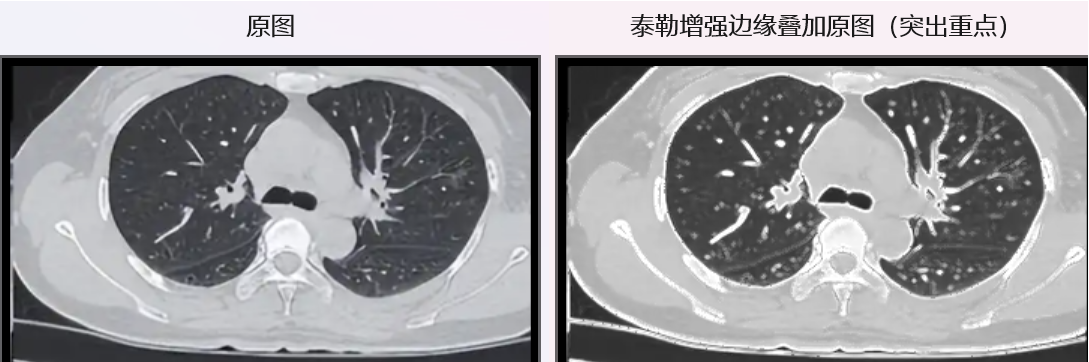
泰勒增强边缘,主动舍弃噪声细节,只强化稳定的真边缘, 线条干净,轮廓突出。
但是 Sobel的保留细节算法也更具有艺术视觉美:

我们看到的泰勒增强边缘里"丢失的细节",恰恰是它的核心价值------舍弃噪声,抓住本质。因此,理论本身没有绝对的"好"与"坏",关键看工程上怎么"用"。

理论与实践的鸿沟
以前我总觉得,数学就像菜市场算账------2块加3块一定是5块,分毫不差。但泰勒级数让我明白,理论数学和工程应用之间,隔着一道巨大的鸿沟。
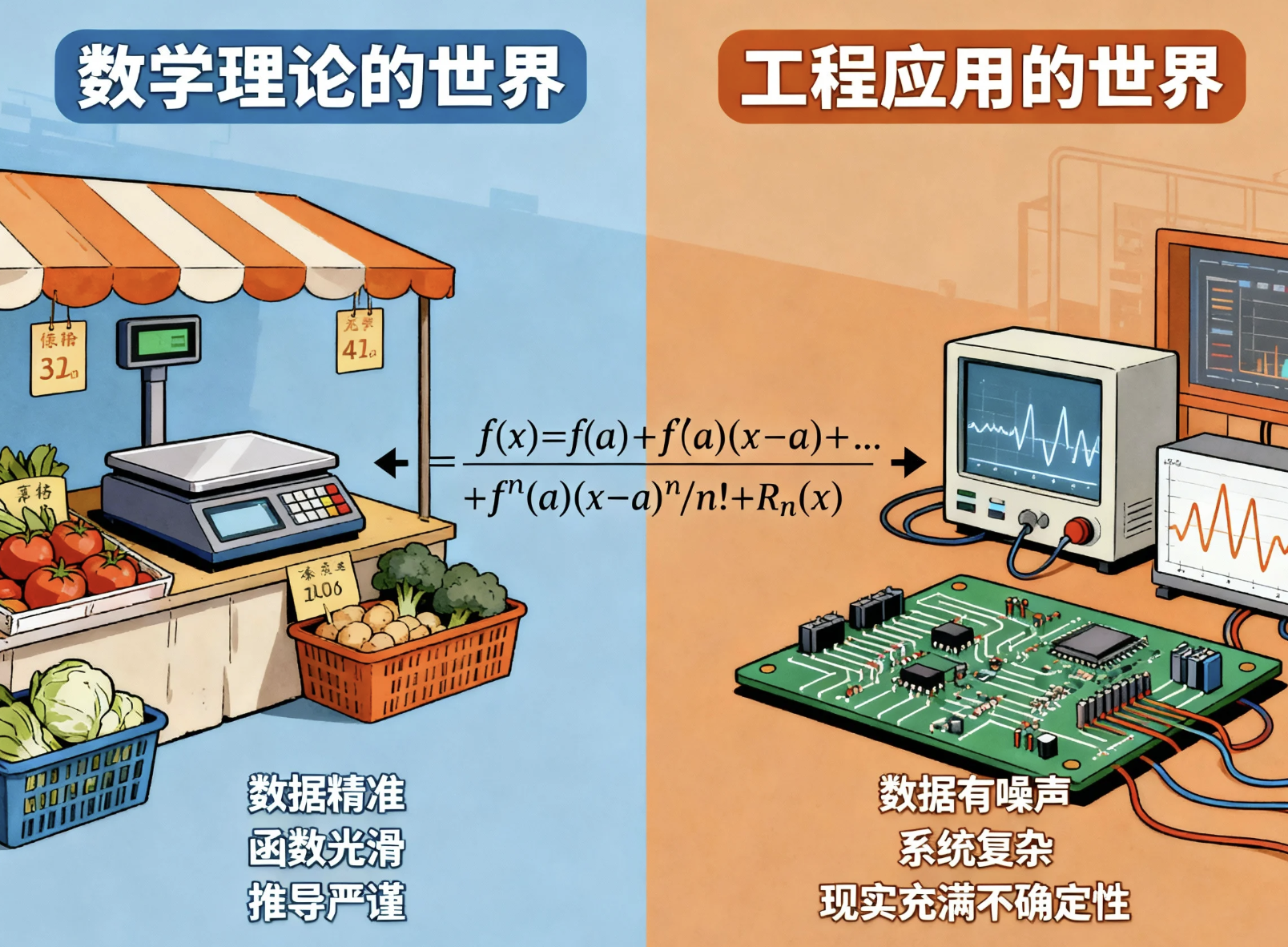
数学理论的世界里,数据精准、函数光滑、推导严谨;但工程的世界里,数据有噪声、系统复杂、现实充满不确定性。
我在做图像处理时,算法在测试环境里跑得顺风顺水,参数调得完美无瑕;可一放到生产环境,面对真实的光线变化、图像模糊,算法直接"罢工"。当时我还埋怨"现实数据不听话",现在才明白,不是现实不听话,是我的预设模型太"理想化"了。
泰勒级数的理论是完美的,但在工程里用的时候,必须做妥协和取舍:
全局拟合时,舍弃高阶项,用分段低阶避免震荡;
边缘检测时,巧用1+2阶项,用高阶敏感过滤噪声;
还要结合滤波、平滑等方法,让理论适配现实。
数学不是"拿来就用"的工具,而是"指导实践"的思想。它告诉我们"理想状态下应该是什么样",而工程师的工作,就是把这种理想,变成"现实里能用的东西"。

理论与实践的代际差,如何迁就
我们身边总有这样的例子:很多先进理论早在几十年前就被提出,却迟迟无法落地。比如深度学习的雏形几十年前就有了,但直到GPU算力提升、大数据爆发才真正火起来;很多图像识别算法理论完美,却受限于早年硬件条件无法应用。
这就是理论与实践的代际差------理论可以跑得很快,但实践需要硬件、数据、工程能力的支撑。
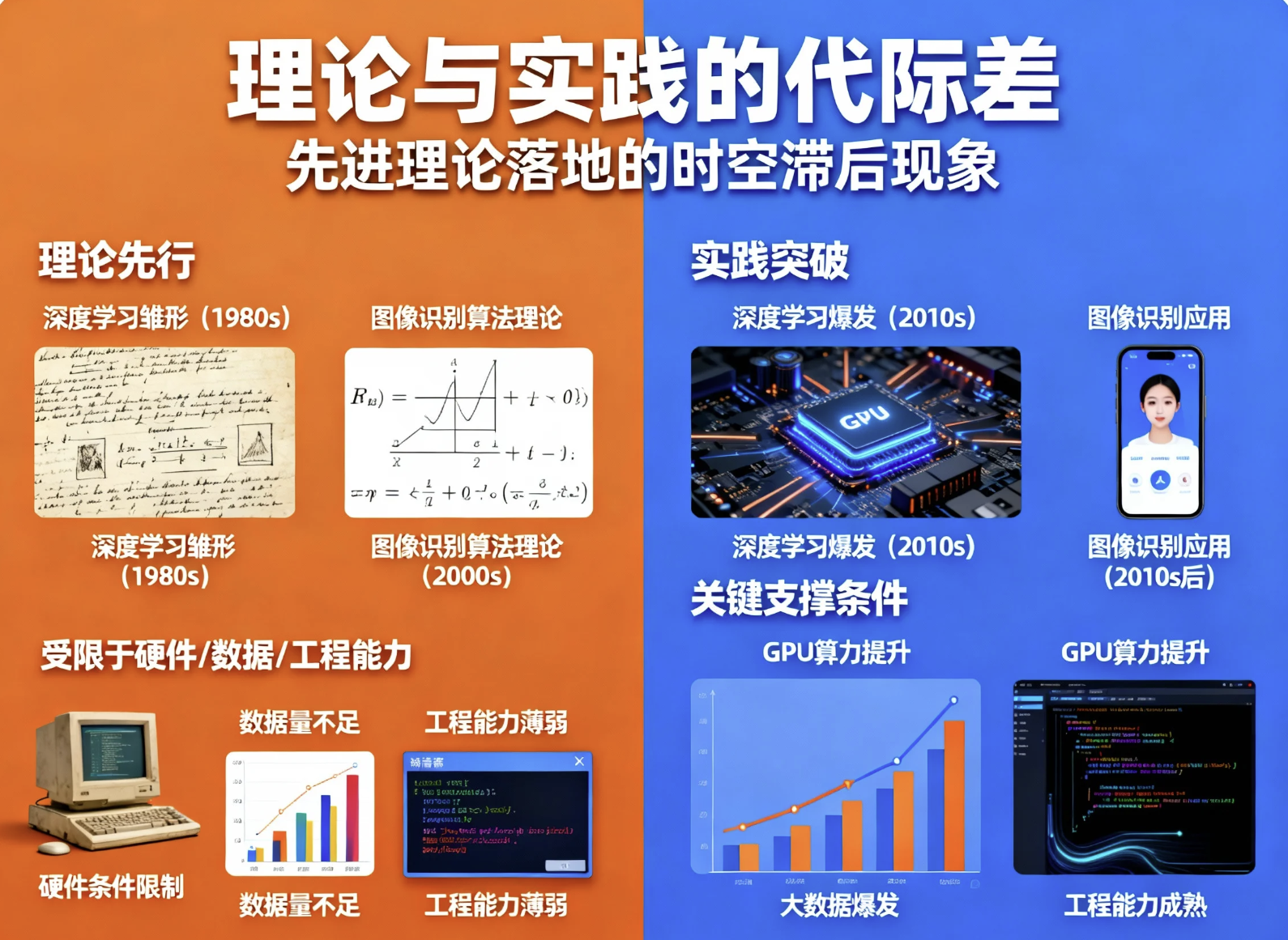
理论超前于实践,是好事吗?当然是。泰勒级数不仅解决了函数计算问题,更奠定了数值分析、信号处理的基础。没有这些超前理论,就没有今天的计算机、手机、人工智能。
但如果理论跑得太远,完全脱离实践,就会变成"空中楼阁"。就像用20阶多项式拟合带噪声的数据,再漂亮的理论,也没有实际价值。
这让我想到两种人:一种是"思想的巨人,行动的矮子",能提出深刻理论,却不擅长落地;另一种是"行动的巨人,思想的矮子",执行力超强,能把简单想法做成大生意,却不擅长深度思考。
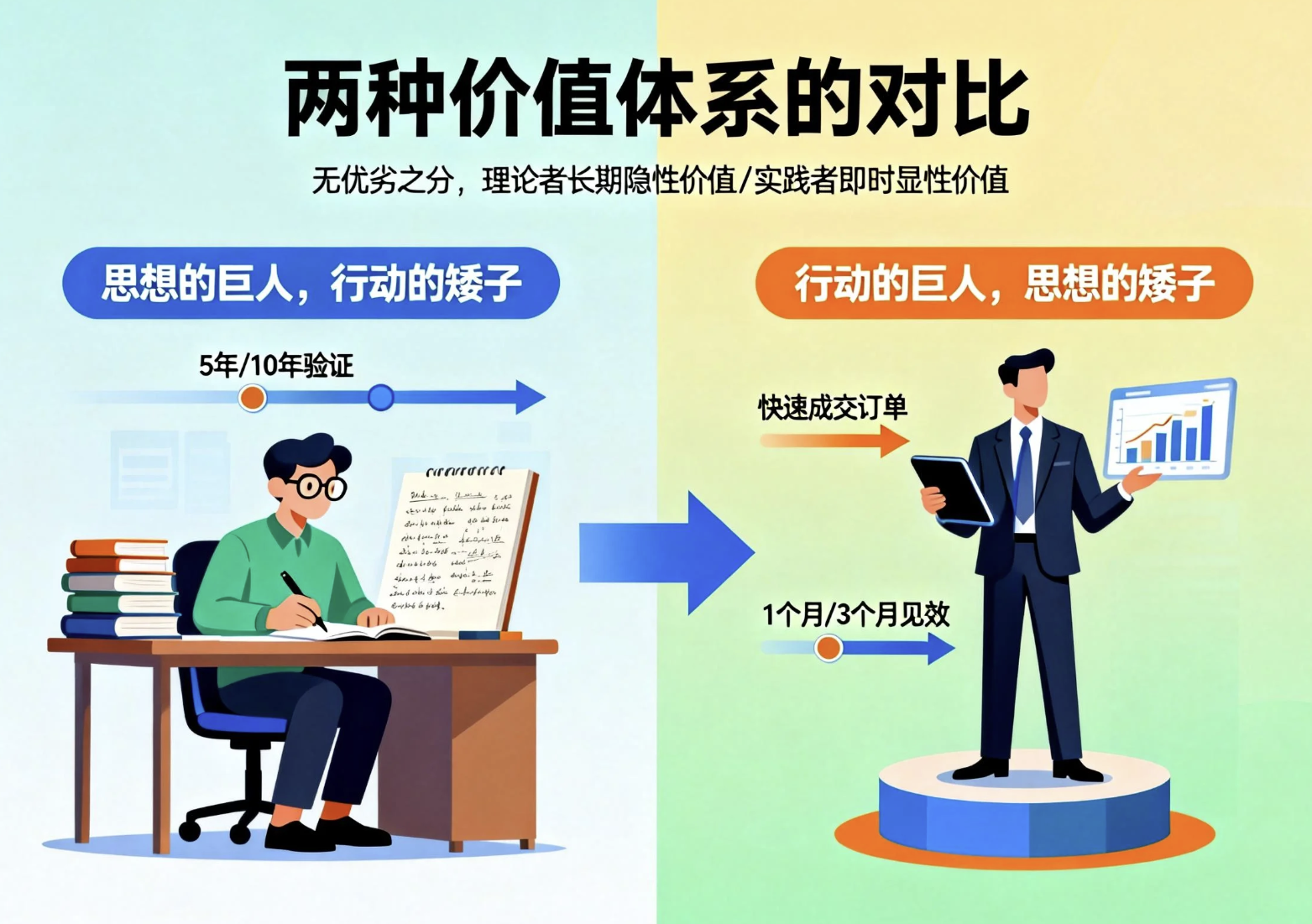
这两种人没有优劣之分,只是属于不同的价值体系。理论研究者的价值是长期隐性的,需要时间验证;实践者的价值是即时显性的,能快速解决现实问题。
最好的状态,是理论和实践互相迁就,互相成就------理论给实践指明方向,实践给理论提供土壤。就像让生意人研究数学、让思考者跑市场,都是对天赋的浪费。

感悟
我们的成长,也是 "从单点深挖,到逐步拓展"的过程,就像泰勒级数一样,先把自己的"局部优势"做深做透,慢慢就能拓展出属于自己的"人生曲线"。
