更弱智的算法学习 day48

单调栈基础

**通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，**此时我们就要想到可以用单调栈了，时间复杂度为O(n)。

739. 每日温度

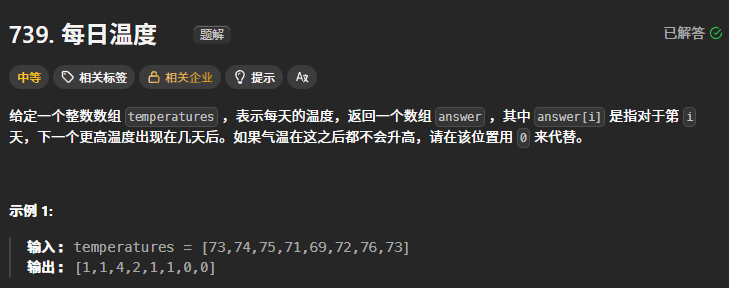
构建一个栈，用来一次存储从大到小的元素（栈底大，栈顶小），从后向前遍历每日温度，和栈订的数据进行比较，可能出现如下的情况：

1：栈内要有元素！！！！

2：第i日温度大于栈顶的温度：

此时栈顶的温度并非最高，由于是从后向前遍历，也即存在栈顶元素之前的某一天，温度高于栈顶，如下图的5和2，也即2不会对前面的时间产生影响（不会成为前面日子升高气温的某一天，因为5代替了他的效果）。因此，pop（）掉没有第i日高的温度。

3：等于：同上理

4：第i日温度小于栈顶的温度：

也即此时可能有贡献，加入到栈中

在执行完弹出操作后，如果栈非空，那么栈顶元素就是距离第 i天右边最近的、温度比它高的日子的索引。因此，等待的天数就是 stack[-1] - i，并将其存入 ans[i]。如果栈为空，则说明右边没有更高的温度，ans[i]保持为0

python 复制代码

class Solution:
    def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
        n = len(temperatures)
        stack = []
        ans = [0]*n

        for i in range(n-1 ,-1 ,-1):
            t = temperatures[i]

            while stack and t >= temperatures[stack[-1]]:
                stack.pop()
            if stack:
                ans[i] = stack[-1] - i
            stack.append(i)

        return ans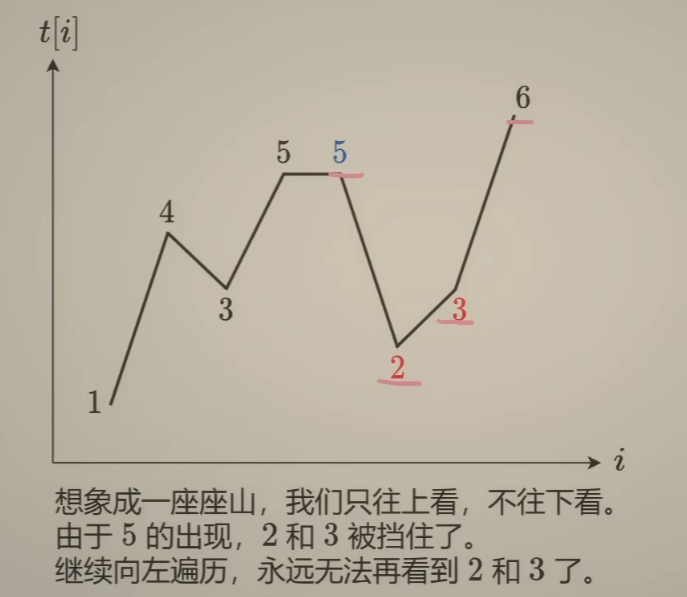

496.下一个更大元素 I

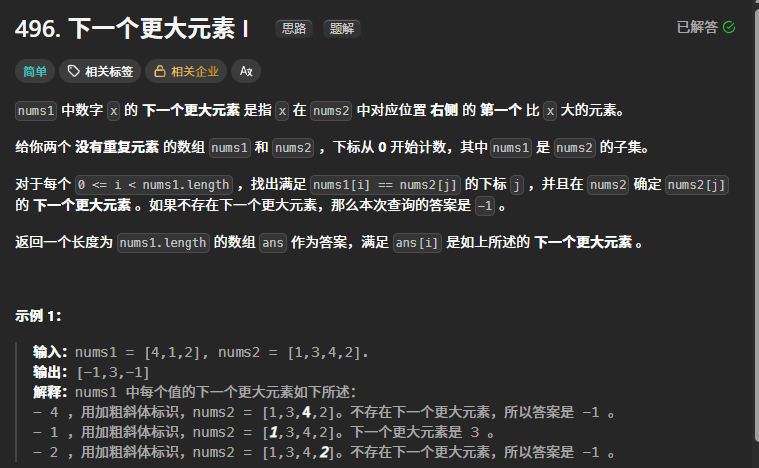
下面是暴力搜索的方法，侥幸没超时

python 复制代码

class Solution:
    def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
        m = len(nums1)
        n = len(nums2)

        ans = [-1] * m
        stack = []

        for i in range(m):
            for j in range(n-1, -1, -1):
                if nums2[j] > nums1[i]:
                    stack.append(nums2[j])
                elif nums2[j] == nums1[i] and stack:
                    ans[i] = stack[-1]
                    print(stack)
            stack = []
        return ans

单调栈方法

考虑建立nums1和nums2之间的映射，然后在nums2中进行单调栈处理即可。

在栈非空且遍历到的元素大于栈顶元素时，也即找到了该栈顶元素的最近的较大数，不断查找栈顶元素在nums1中是否存在，存在的话就存储到结果中。

处理完之后加入栈中

python 复制代码

class Solution:
    def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
        m = len(nums1)
        n = len(nums2)

        idx = {x:i for i,x in enumerate(nums1)}
        ans = [-1] * m
        stack = []

        for p in range(n):
            while stack and nums2[p] > nums2[stack[-1]]:
                k = stack.pop()
                if nums2[k] in idx:
                    ans[idx[nums2[k]]] = nums2[p]
            stack.append(p)
        return ans

503.下一个更大元素II

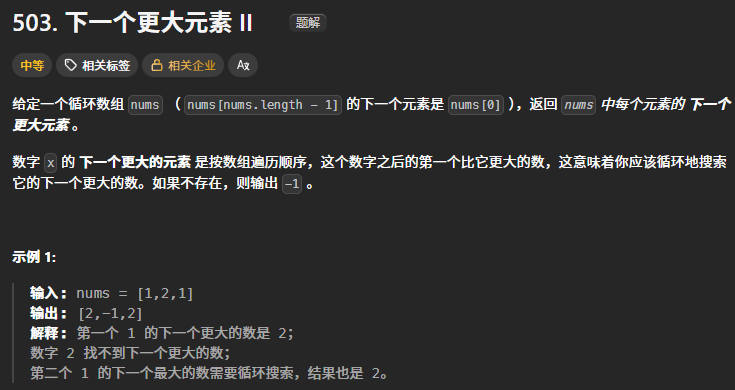
和上面一题思路非常类似，由于存在循环，可以将数组扩展复制一份继续检查，也即实现了循环的效果

python 复制代码

class Solution:
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        n = len(nums)
        ans = [-1]*n
        stack = []

        for i in range(n):
            nums.append(nums[i])

        for j in range(2*n):
            while stack and nums[j] > nums[stack[-1]]:
                k = stack.pop() 
                if k < n:
                    ans[k] = nums[j]
            stack.append(j)

        return ans