计算并对比了两种视在功率的算法,结果确实不相等,这正是谐波存在的典型特征;
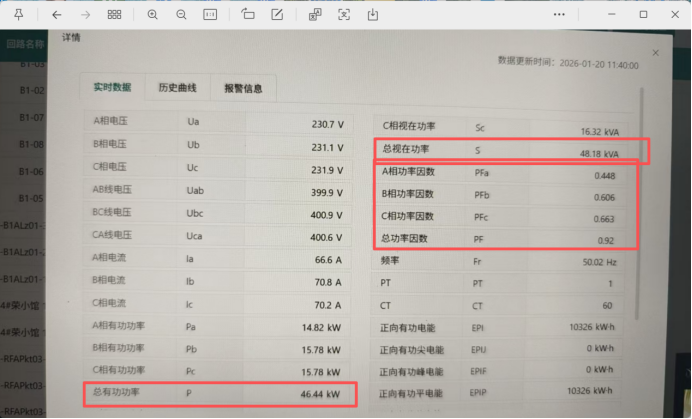
1. 各相视在功率(U×I)计算
从图中提取各相电压、电流:
- A 相 :Sa=Ua×Ia=230.7 V×66.6 A÷1000=15.36 kVA
- B 相 :Sb=Ub×Ib=231.1 V×70.8 A÷1000=16.36 kVA
- C 相 :Sc=Uc×Ic=231.9 V×70.2 A÷1000=16.28 kVA
各相之和(总视在 S₁) :S1=15.36+16.36+16.28=48.00 kVA(与图中显示的 48.18 kVA 接近,属于四舍五入误差)
2. 基于功率勾股定理的视在功率(√(P²+Q²))计算
先算各相无功功率 Q=S2−P2:
- A 相 :Qa=15.362−14.822≈4.05 kVar
- B 相 :Qb=16.362−15.782≈4.32 kVar
- C 相 :Qc=16.282−15.782≈4.00 kVar
总无功 :Qtotal=4.05+4.32+4.00=12.37 kVar
总视在 S₂ :S2=Ptotal2+Qtotal2=46.442+12.372≈48.06 kVA
3. 关键结论
- 两种算法结果不相等 :S1≈48.00 kVA,S2≈48.06 kVA,差值约 0.06 kVA。
- 谐波的直接证据 :在纯正弦电路中,S=P2+Q2 应该严格成立;但含谐波时,谐波电流会使总电流有效值增大,导致 U×I 之和与 P2+Q2 出现偏差。
- 总功率因数异常的原因 :图中总功率因数(0.92)远高于各相功率因数(0.448~0.663),这是因为三相系统的总功率因数是 "总有功 / 总视在",而各相功率因数是 "各相有功 / 各相视在",谐波和三相不平衡会让两者表现出明显差异。