【SimpleITK】从 Python 闭包到空间几何

在医学图像配准（Registration）的任务中，SimpleITK 是最常用的工具库。然而，官方示例代码中往往隐藏着许多 Python 高级特性（如闭包）和医学图像特有的空间几何逻辑（如物理坐标转换）。

本文将抽丝剥茧，不仅讲解配准原理，更要深入拆解代码中那些**"容易被忽视但至关重要"**的技术细节。

---

一、Python 进阶：回调函数中的 lambda 与闭包

在配置配准过程的监控（Visualization）时，你会看到这样一段代码：

Python

# 注册迭代事件的回调函数
registration_method.AddCommand(
    sitk.sitkIterationEvent,
    lambda: rc.metric_and_reference_plot_values(
        registration_method, fixed_points, moving_points
    ),
)

1. 为什么要用 lambda？

这里使用 lambda 不是为了简便，而是为了解决函数签名（Function Signature）不匹配的问题。

• API 限制 ：AddCommand 方法要求传入的回调函数（Callback）必须是无参数 的函数指针，即 void function()。

• 实际需求 ：我们的绘图函数 rc.metric_and_reference_plot_values 需要参数 。它必须访问 registration_method（获取当前 Metric 值）和 points（计算 TRE）。

2. 闭包（Closure）的魔法

为了解决上述冲突，我们使用了 闭包 技术：

• lambda 定义了一个匿名函数，该函数本身不接收参数（符合 API 要求）。

• 但在函数体内部，它通过闭包（Closure） 捕获了外部作用域中的变量 registration_method, fixed_points, moving_points。

• 当 sitkIterationEvent 触发时，SimpleITK 调用这个无参 lambda，lambda 内部再带着捕获的变量去调用实际的绘图函数。

---

二、核心策略：多分辨率金字塔 (Multi-Resolution)

配准中最核心的配置如下：

Python

registration_method.SetShrinkFactorsPerLevel(shrinkFactors=[4, 2, 1])
registration_method.SetSmoothingSigmasPerLevel(smoothingSigmas=[2, 1, 0])
registration_method.SmoothingSigmasAreSpecifiedInPhysicalUnitsOn()

深度解析

这是让配准既快 又准的"三步走"战略（Coarse-to-Fine）：

1. Level 0 (Shrink=4, Sigma=2mm)：

   • 动作：图像缩小 4 倍，且进行高斯模糊。

   • 目的 ：极速粗配准。模糊细节，让优化器只看"大轮廓"，避免陷入局部极小值。

2. Level 1 (Shrink=2, Sigma=1mm)：

   • 动作：图像缩小 2 倍，轻微模糊。

   • 目的：进一步细化位置。

3. Level 2 (Shrink=1, Sigma=0)：

   • 动作：原始分辨率，不模糊。

   • 目的 ：精细微调，达到最终精度。

4. 关于单位 (PhysicalUnitsOn)：

   • 这行代码强制告诉 ITK：上面的 [2, 1, 0] 单位是毫米（mm），而不是像素个数。这保证了在不同分辨率的 CT/MRI 数据上，平滑的物理程度是一致的。

---

三、结果评估：可视化图表的玄机

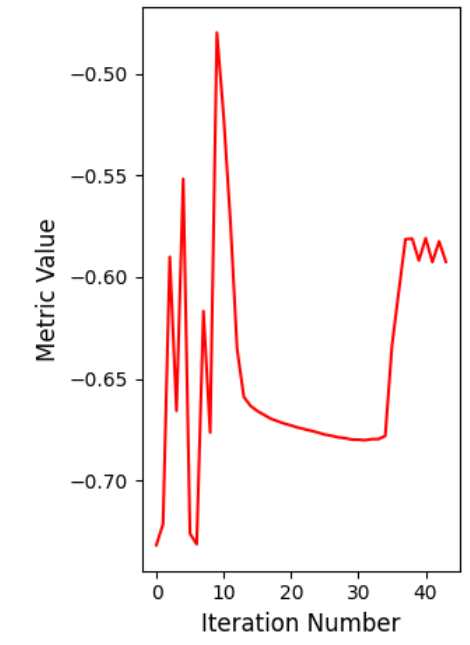
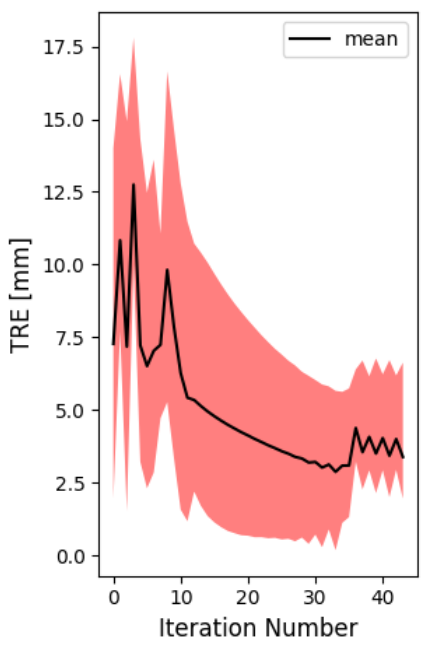
1. 实时监控图（折线图）

• 为什么曲线会跳变？

  • 你会发现 Metric 曲线在迭代过程中有几次剧烈的"断崖式"跳跃。这正是金字塔层级切换的标志。

  • 从模糊图像切换到清晰图像，计算 Metric 的基准变了，分数自然不同。这是正常的。

• 阴影面积代表什么？

  • 右侧 TRE 图中的红色阴影代表 误差的标准差 (Std Dev)。

  • 阴影越宽 ：说明点与点之间的误差差异大（有的准，有的歪），通常意味着存在旋转偏差。

  • 阴影越窄：说明大家误差都很均匀，配准结果稳定。

2. 最终结果图（3D 散点图）

• 色条的含义 ：如果不强制设置 min/max，程序会根据当前结果自动归一化颜色。

  • 黑色/红色 = 误差最小的区域。

  • 亮黄色/白色 = 误差最大的区域。

• 临床意义 ：这张图能揭示空间不均匀性 。比如中心区域（旋转轴）可能是黑色的（准），但边缘区域是黄色的（误差大）。只看平均值是无法发现这种"杠杆效应"带来的边缘误差的。

---

四、硬核数学：ROI 筛选与坐标转换

在临床评估中，我们往往只需要计算脑部区域的误差，需要剔除背景噪点。这涉及到了复杂的空间几何操作。

Python

# 1. 忽略背景，计算包围盒
label_shape_analysis.SetBackgroundValue(0) 
label_shape_analysis.Execute(roi)
bounding_box = label_shape_analysis.GetBoundingBox(1)

# 2. 核心难点：像素索引 -> 物理坐标
sub_image_max = fixed_image.TransformIndexToPhysicalPoint(
    (
        bounding_box[0] + bounding_box[3] - 1, # X轴终点
        bounding_box[1] + bounding_box[4] - 1, # Y轴终点
        bounding_box[2] + bounding_box[5] - 1, # Z轴终点
    )
)

Q1：SetBackgroundValue(0) 是什么意思？

roi 是二值图像（0为背景，1为人体）。这句话明确告诉统计滤波器："请忽略数值为 0 的区域，只计算数值为 1（即人体）的几何形状。"

Q2：像素如何转物理坐标？

SimpleITK 中的图像带有元数据（Metadata）：

• Origin (原点)

• Spacing (间距/步长)

• Index (第几个像素)

转换公式为：

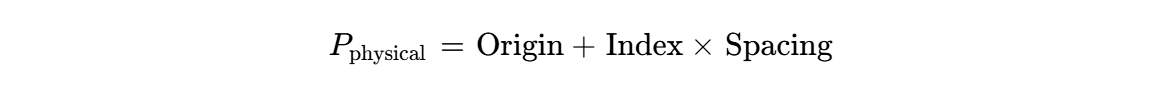
代码中的 TransformIndexToPhysicalPoint 就是在执行这个公式。

Q3：为什么计算 Max 时要 -1？

这是一个经典的栅栏问题（Off-by-one error）。

• 假设包围盒 X 轴起点索引是 10，长度是 5。

• 它占据的像素是：10, 11, 12, 13, 14。

• 最后一个像素的索引是 14。

• 计算公式：。

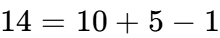• 如果直接用 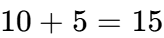，第 15 号像素已经在盒子外面了。必须减 1 才能定位到物体边缘的那个像素。

Q4：筛选逻辑

最后，利用计算出的物理空间立方体（Bounding Box），使用 zip 遍历所有解剖点对，通过简单的 if 判断：

Python

if min_x <= p[0] <= max_x and ... :
    keep_point()

这实现了**"只保留落在脑壳里的点，剔除外面干扰点"**的严谨评估逻辑。

---

希望这篇总结能帮到正在学习 SimpleITK 的你！如果有帮助，请点赞收藏。