目录
[为什么会形成"倒 V 字形"?](#为什么会形成“倒 V 字形”?)
[为什么 125 kHz 的低通滤波器没有把它滤掉?](#为什么 125 kHz 的低通滤波器没有把它滤掉?)
前言
该笔记是针对 4MHz 采样信号的 250kHz 下采样抗混叠滤波器验证测试及故障排除的记录。
1.抗混叠滤波器未开启或不起作用时
1.1现象
采集的信号是100hz~250khz的信号,当125khz的低通抗混叠滤波器未开启或参数设置不正确时,下采样的结果如下: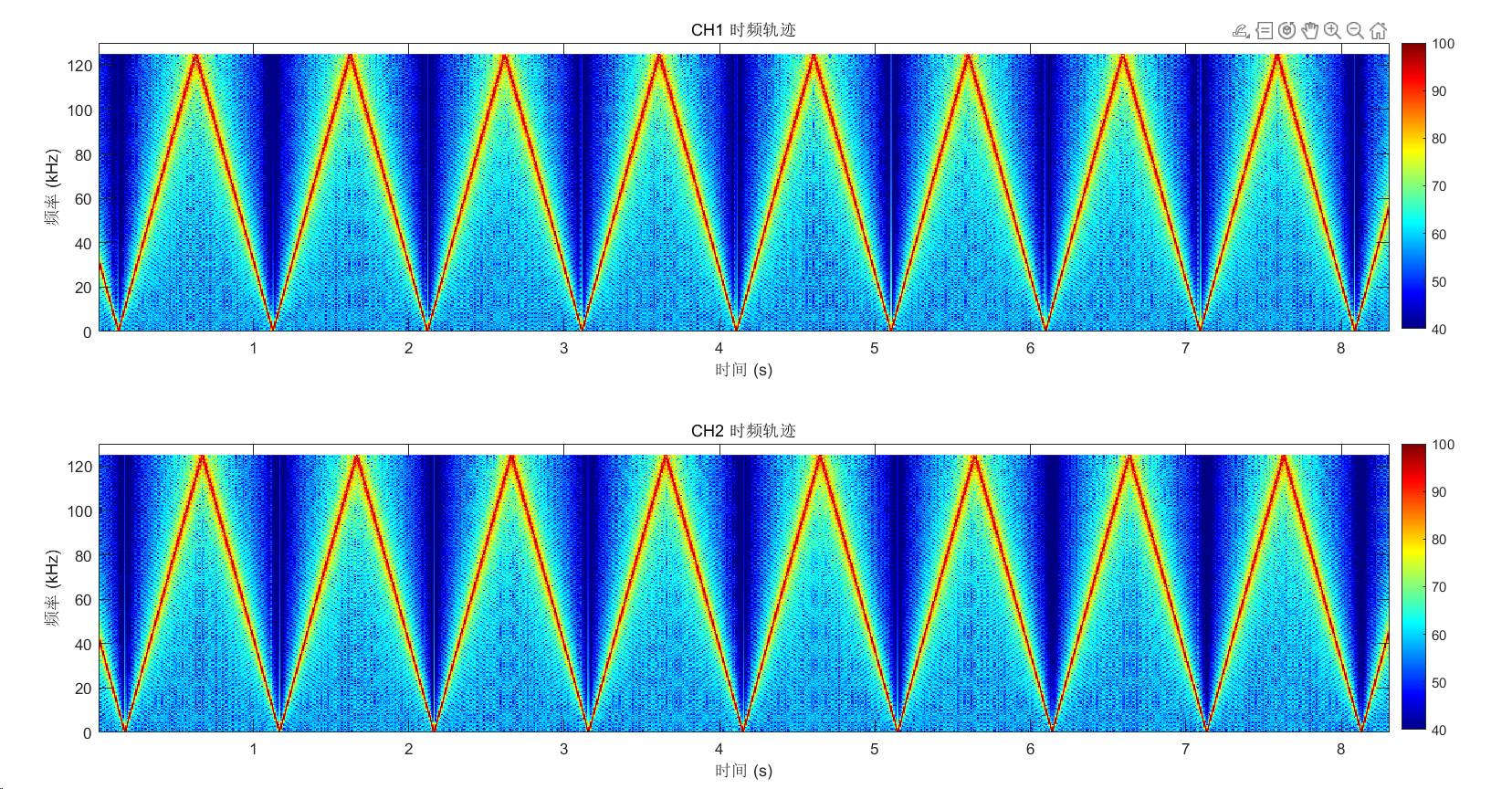
这个频谱图反映信号处理中的经典问题------频率混叠(Aliasing)。虽然使用了 125 kHz 的低通滤波器,但图中出现的"倒 V 字形"(或三角形)轨迹说明,超出 125 kHz 的扫频信号并没有被完全滤除,并且在采样过程中发生了"折返"。
1.2原因
以下是详细的原因分析:
为什么会形成"倒 V 字形"?
这主要是由采样频率(Sampling Rate)和奈奎斯特准则(Nyquist Theorem)决定的。
奈奎斯特频率: 从图中 Y 轴可以看到,显示的最高频率正好是 125 kHz 。这是因为系统采样率
是 250 kHz。根据采样定理,系统能处理的最大不失真频率就是采样率的一半,即 125 kHz。
频率折叠(Folding): 当你的扫频信号从 100 Hz 上升到 125 kHz 时,频谱图上显示的是正常的上升线。
混叠发生: 当信号继续从 125 kHz 上升到 250 kHz 时,由于这部分频率超过了系统的处理上限,它们会以 125 kHz 为"镜面"发生镜像折返。
例如:当扫频信号到达 150 kHz 时,在频谱上会显示在
的位置。
当扫频信号到达 250 kHz 时,在频谱上会显示在
的位置。
结论: 这种"上升再下降"的视觉效果,实际上是线性扫频信号在经过采样节点时,高频部分折返回基带的结果。
为什么 125 kHz 的低通滤波器没有把它滤掉?
理论上,如果你接了 125 kHz 的低通滤波器(LPF),超过 125 kHz 的信号应该变弱甚至消失。图中依然有明亮的红色轨迹(强信号)折返,可能有以下几种原因:
滤波器类型与阶数: 滤波器并不是像"墙"一样在 125 kHz 处瞬间切断。如果滤波器的阶数较低(斜率较缓),150 kHz 或 200 kHz 的信号依然会有很大的残余能量通过。
数字滤波器 vs 模拟滤波器: 如果这个滤波器是数字滤波器 (在采样之后处理),那么它无法阻止混叠。因为混叠在 ADC(模数转换)采样的瞬间就已经发生了。(lhw:但是由于一开始采样的频率是4Mhz,所以不存在这种原因。)
- 要防止这种现象,必须在采样之前使用模拟抗混叠滤波器(Anti-aliasing Filter)。
信号强度过大: 如果输入扫频信号的功率非常高,即使滤波器衰减了 20-30 dB,剩余的能量在频谱图(通常是对数坐标)上看起来依然可能非常明显。
如何判断结果是否"正确"?
如果目的是观察混叠: 那么这个图非常完美,它清晰地展示了信号如何折返。
如果目的是测试滤波器的截止特性: 那么这个结果说明你的滤波器性能不足 (抑制效果不够)或者位置放错了(应该放在采样前端且使用模拟滤波器)。
总结建议
如果你希望频谱图只显示 0-125 kHz 的上升段,而不出现倒 V 字:
提高采样率: 将采样率提高到 500 kHz 以上,这样 250 kHz 的扫频信号就在奈奎斯特频率之内。
加强前端滤波: 在信号进入采集卡之前,加一个更陡峭的模拟低通滤波器。
缩小扫频范围: 将扫频范围限制在 100 Hz ~ 125 kHz 之间。
2.当抗混叠滤波器起作用时
2.1现象
采集的信号是100hz~250khz的信号,当125khz的低通抗混叠滤波器未开启或参数设置不正确时,下采样的结果如下:
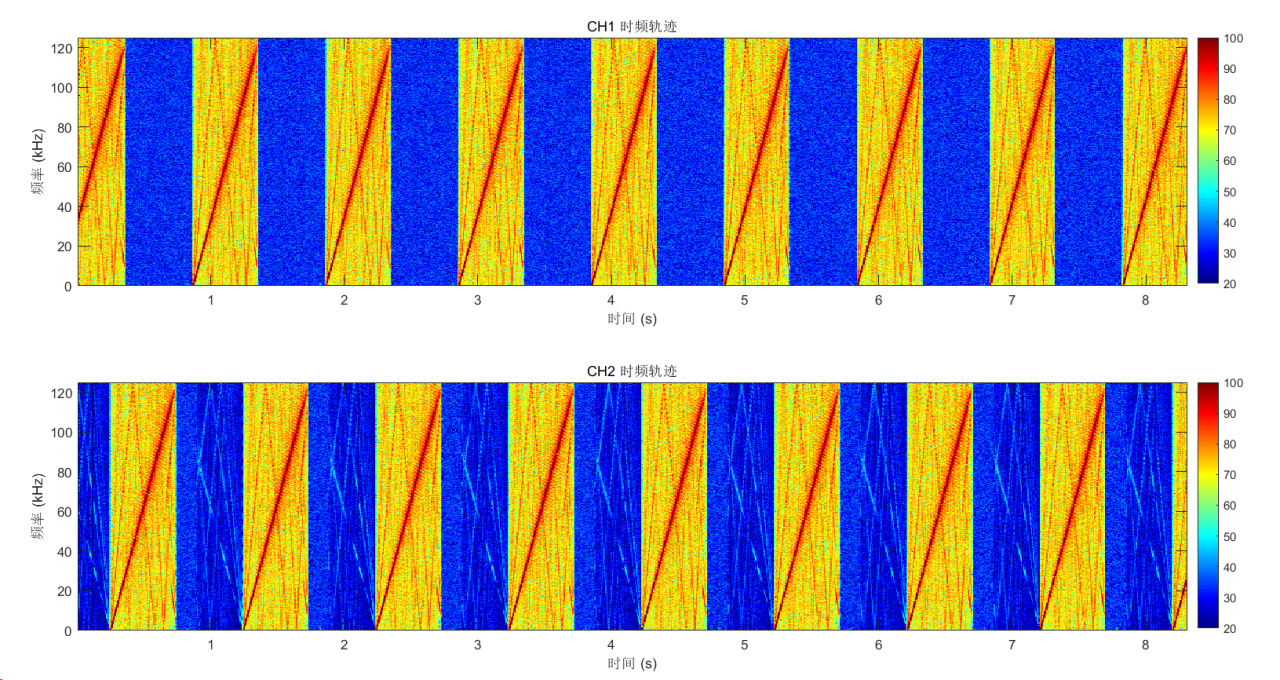
该图是一个比较理想的频谱图,只保留截止频率以下的成分,而将除此之外的部分滤除。
根据滤波器的特性,线条的颜色(能量)会有以下变化:
-
通带(< 125 kHz): 信号线是深红色,表示能量几乎没有损耗地通过。
-
过渡带(接近 125 kHz): 线条颜色从红色转为黄色、绿色,表示信号开始被衰减。
-
阻带(> 125 kHz): 信号线变为深蓝色或消失,表示信号被完全抑制。
以上现象就是抗混叠滤波器起作用那个的结果,这也是用来验证设计的滤波器是否正确的一种方法。
3.FPGA滤波器性能和参数生成代码
为了便于验证所设计的滤波器性能 ,因此编写了包含滤波器系数设计 、扫频信号仿真检验 以及 Verilog 硬件参数生成功能的完整代码,如下所示:
%% FIR 滤波器全流程:250kHz 下采样 (标注增强版)
clc; clear; close all;
% ========================== 1. 开关与配置 ==========================
Enable_Sim = true;
Enable_COE = true;
Enable_Verilog = true;
fs_raw = 4e6; % 原始采样率 4MHz
fs_target = 250e3; % 目标采样率 250kHz
f_cutoff = fs_target / 2; % 抗混叠截止频率 (125kHz)
% 阶数
N = 128; %FPGA的dsp资源有限,不宜过高
filename_str = sprintf('filter_params_%dk_N%d', fs_target/1000, N);
path_coe = './coe/'; path_v = './v/';
% ========================== 2. 滤波器设计 ==========================
f_nyquist = fs_raw / 2;
% 过渡带预留:从 110kHz 到 125kHz
Wn = [300/f_nyquist, 110e3/f_nyquist];
b = fir1(N, Wn, 'bandpass');
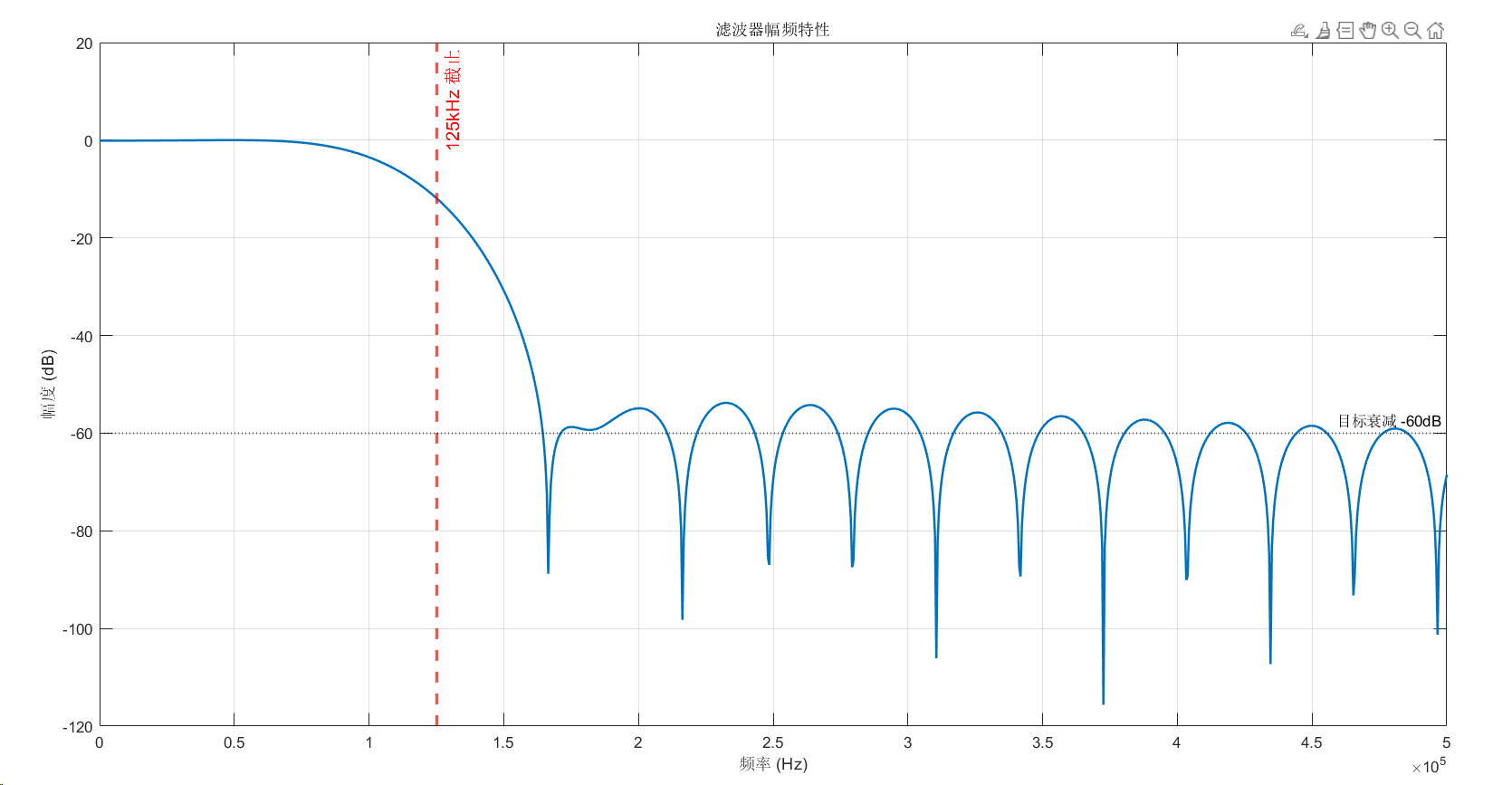
% --- 验证图 1: 频率响应图添加 125kHz 标注 ---
figure('Name', '滤波器响应验证', 'Color', 'w');
[h, f] = freqz(b, 1, 1024*4, fs_raw);
plot(f, 20*log10(abs(h)), 'LineWidth', 1.5);
grid on; hold on;
% 标注 125kHz 拦截位置 (X轴单位为 Hz)
xline(f_cutoff, '--r', '125kHz 截止', 'LineWidth', 2, 'LabelOrientation', 'aligned', 'FontSize', 12);
% 标注阻带衰减目标 (例如 -60dB)
yline(-60, ':k', '目标衰减 -60dB', 'LineWidth', 1);
title('滤波器幅频特性');
xlabel('频率 (Hz)'); ylabel('幅度 (dB)');
xlim([0 500e3]); % 重点观察 0-500kHz
% 定点化处理
scale = 32767;
B_int = round(b / max(abs(b)) * scale);
hex_datas = cell(length(B_int), 1);
for i = 1:length(B_int)
val = B_int(i);
if val < 0, val = 65536 + val; end
hex_datas{i} = lower(dec2hex(val, 4));
end
% ========================== 3. 仿真检验 ==========================
if Enable_Sim
t_duration = 0.1;
t_sim = 0:1/fs_raw:t_duration;
s_sweep = chirp(t_sim, 100, t_sim(end), 250e3);
s_filt = filter(b, 1, s_sweep);
figure('Name', '时频分析验证', 'Color', 'w');%'Position', [100, 100, 1000, 750]
% --- 子图 1: 滤波前 ---
subplot(2,1,1);
[S1, F1, T1] = spectrogram(s_sweep, 2048, 1024, 2048, fs_raw, 'yaxis');
PSD1 = 20*log10(abs(S1) + eps);
imagesc(T1*1000, F1/1000, PSD1);
axis xy; colormap('jet'); hold on;
% 标注 125kHz 拦截位置 (Y轴单位已转换为 kHz)
yline(f_cutoff/1000, '--w', '125kHz', 'LineWidth', 2, 'FontSize', 11);
title('滤波前 (0-250kHz 扫频)'); ylabel('频率 (kHz)'); xlabel('时间 (ms)');
ylim([0 300]); clim([30 90]); colorbar;
% --- 子图 2: 滤波后 ---
subplot(2,1,2);
[S2, F2, T2] = spectrogram(s_filt, 2048, 1024, 2048, fs_raw, 'yaxis');
PSD2 = 20*log10(abs(S2) + eps);
imagesc(T2*1000, F2/1000, PSD2);
axis xy; colormap('jet'); hold on;
% 标注 125kHz 拦截位置
yline(f_cutoff/1000, '--w', '125kHz 拦截点', 'LineWidth', 2, 'FontSize', 11);
title('滤波后 (观察 125kHz 以上能量衰减)');
ylabel('频率 (kHz)'); xlabel('时间 (ms)');
ylim([0 300]); clim([30 90]); colorbar;
end
% ========================== 4. 生成 .coe 文件 ==========================
if Enable_COE
if ~exist(path_coe, 'dir'), mkdir(path_coe); end
fid = fopen([path_coe, filename_str, '.coe'], 'w');
fprintf(fid, 'memory_initialization_radix=16;\n');
fprintf(fid, 'memory_initialization_vector=\n');
for i = 1:length(hex_datas)
if i == length(hex_datas), fprintf(fid, '%s;', hex_datas{i});
else, fprintf(fid, '%s,\n', hex_datas{i}); end
end
fclose(fid);
fprintf('COE 生成成功。\n');
end
% ========================== 5. 生成 Verilog 模块 ==========================
if Enable_Verilog
if ~exist(path_v, 'dir'), mkdir(path_v); end
fid = fopen([path_v, filename_str, '.v'], 'w');
fprintf(fid, '/* FPGA FIR Filter Params Array */\n');
fprintf(fid, '`default_nettype none\nmodule %s(\n', filename_str);
fprintf(fid, ' output wire [%d:0] params\n);\n\n', length(hex_datas)*16-1);
for i = 1:length(hex_datas)
fprintf(fid, ' assign params[%d:%d] = 16''h%s;\n', ...
(i-1)*16+15, (i-1)*16, hex_datas{i});
end
fprintf(fid, 'endmodule\n');
fclose(fid);
fprintf('Verilog 生成成功。\n');
end以下是代码运行的结果:
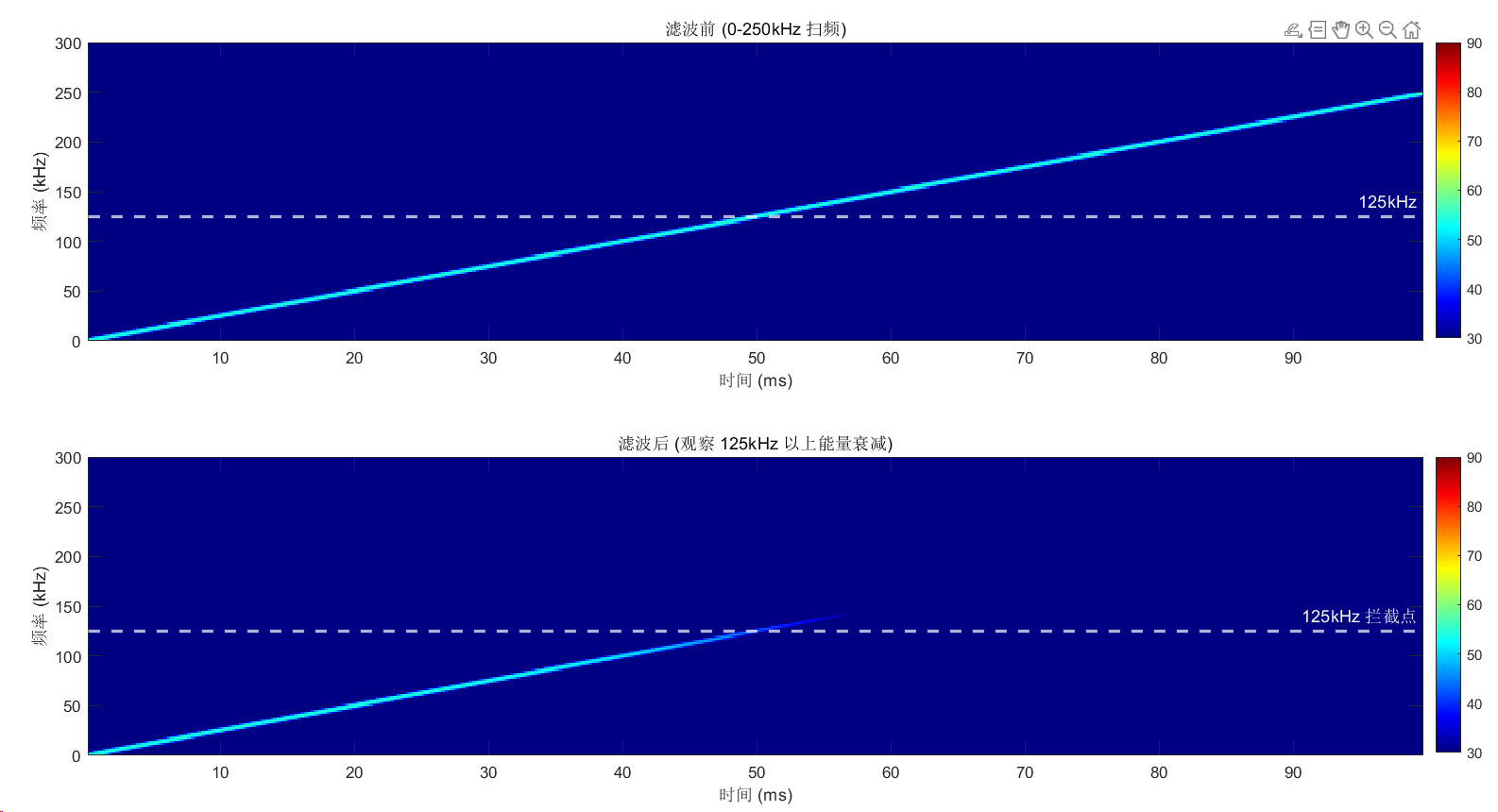
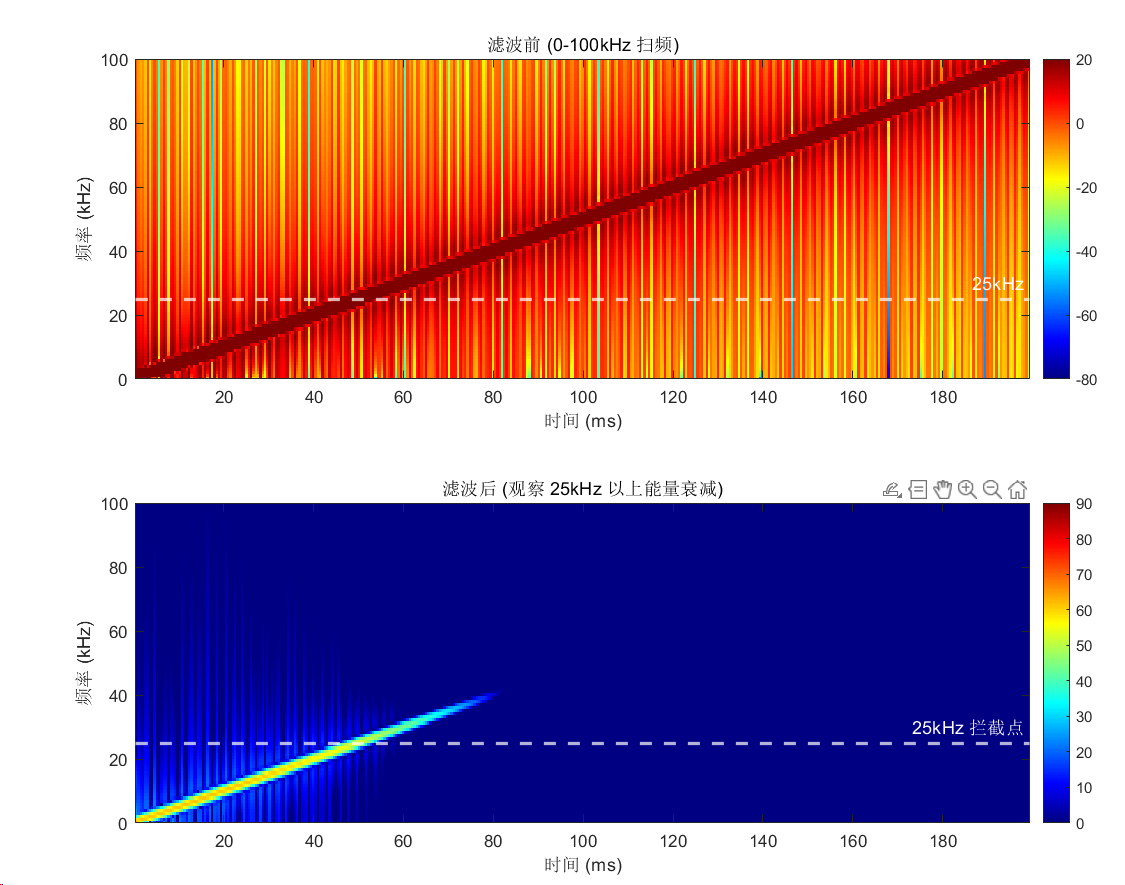
图中的现象说明抗混叠滤波器起到了效果,能把高于125khz的频率衰减。至于说衰减的结果能否达到预期要求,目前我也不知道怎么判断。
在跑代码的过程中,发现无论阶数有多高,都无法完全把信号衰减掉。
再放几张图在这里保存一下:
以上就是本次笔记的内容。